Prólogo

Además de mi artículo reciente, también me gustaría hablar sobre el tema de MU ( M ulti U ser) MIMO. Ya he mencionado un artículo muy famoso del profesor Haardt donde, junto con sus colegas, propone un algoritmo para separar a los usuarios en un enlace descendente basado en métodos lineales, a saber, la Diagonalización en bloque de un canal. El artículo tiene una cantidad impresionante de citas , y también es la publicación fundamental para una de las tareas del examen. Por lo tanto, ¿por qué no entender los conceptos básicos del algoritmo propuesto?

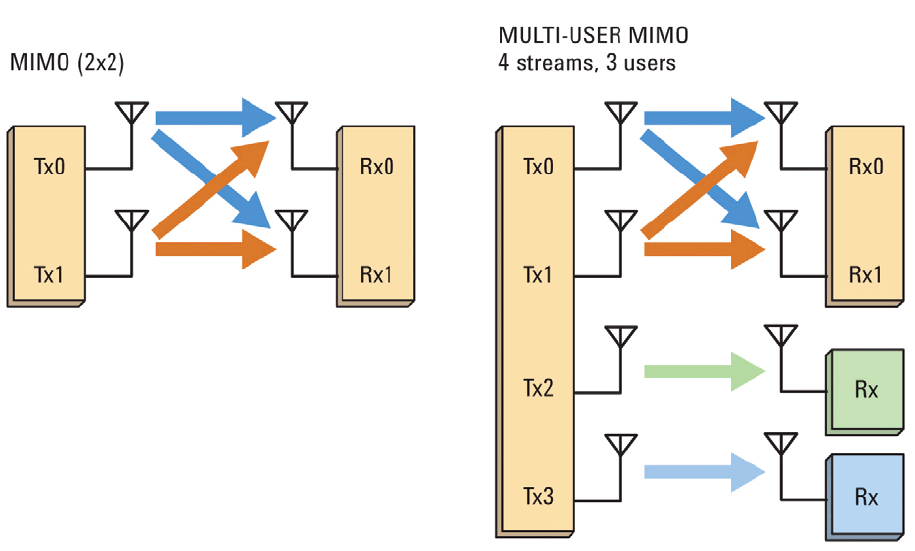
Declaración del problema.

Primero, decidamos en qué área del tema MIMO trabajaremos ahora.
Convencionalmente, todos los métodos de transferencia dentro del marco de la tecnología MIMO se pueden dividir en dos grupos principales:

• Diversidad espacial

El objetivo principal es aumentar la inmunidad al ruido de la transmisión. Los canales espaciales, si se simplifican, se duplican entre sí, por lo que obtenemos la mejor calidad de transmisión.

Ejemplos:
- Códigos de bloque (por ejemplo, el esquema Alamuti );
- Códigos basados ​​en el algoritmo de Viterbi.

• Multiplexación espacial

El objetivo principal es aumentar la velocidad de transmisión. Ya discutimos en un artículo anterior que, bajo ciertas condiciones, el canal MIMO puede considerarse como una serie de canales SISO paralelos. En realidad, esta es la idea central de la multiplexación espacial: lograr el número máximo de flujos de información independientes. El principal problema en este caso es la supresión de la interferencia entre canales (interferencia entre canales) , para lo cual existen varias clases de soluciones:

- separación horizontal del canal;
- vertical (por ejemplo, el algoritmo V-BLAST);
- diagonal (por ejemplo, el algoritmo D-BLAST).

Pero esto, por supuesto, no es todo.

La idea de multiplexación espacial se puede ampliar: para dividir no solo los canales, sino también los usuarios (SDMA - Acceso múltiple de la división espacial).

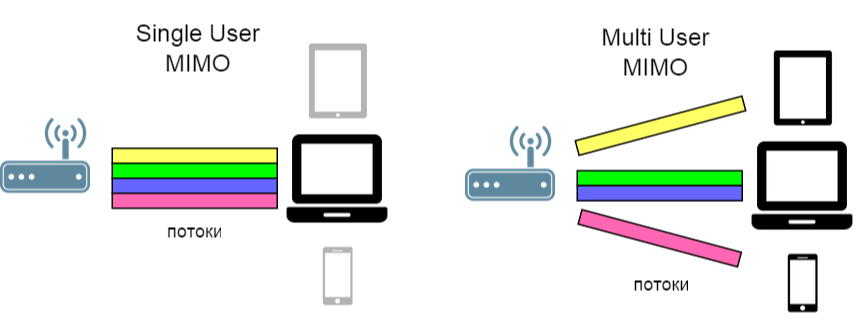
( enlace a la fuente de la ilustración )

En consecuencia, en este caso, ya es necesario luchar contra la interferencia entre usuarios . Para esto, se propuso un algoritmo llamado Block diagonalization Zero-Forcing , que estamos considerando hoy.

Descripción matemática

Comencemos, como antes, con el modelo de señal recibida. Más precisamente, mostramos en el diagrama de dónde y qué proviene:

La matriz de canales en este caso tiene la forma:

con el número total de antenas de transmisión , y el número total de antenas receptoras .

Importante :
Este algoritmo solo se puede aplicar siempre que el número de antenas de transmisión sea mayor o igual que el número total de antenas de recepción:

Esta condición afecta directamente las propiedades de diagonalización.

Entonces, el modelo de los símbolos recibidos (señales) se puede escribir en forma de vector como:

Sin embargo, es más interesante mirar la fórmula para un usuario específico:

De hecho:

• Es una señal útil para el k-ésimo usuario,

  
  

• - esto es interferencia de otros usuarios,

  
  

• - ruido aditivo.

Entonces llegamos a la formulación de la tarea principal:

Puedes encontrar tales matrices para que la parte de interferencia llegue a cero!

Esto es lo que haremos.

Descripción del algoritmo

Realizaremos la descripción con un ejemplo, y como ilustración daré capturas de pantalla de primera mano , comentando un poco sobre ellas.

Considere el primer usuario:

Hablemos de los pasos principales:

• Hacemos una matriz de las matrices de canales de todos los demás usuarios.

• Lo descomponemos usando el método SVD .

  
  

• En la matriz encontramos el subespacio de ruido (null-subespacio) - la matriz (es decir, todo lo que va más allá del rango de la matriz - denotarlo )

  
  

• A partir de esta matriz de ruido y su conjugación hermitiana, compusimos alguna matriz de proyección. .

  
  

Adelante

• Ahora la parte original de la matriz de canales multiplicar con la matriz de proyección resultante .

  
  

• Descomponemos el resultado a través de SVD.

  
  

• En la matriz elegir líneas donde - rango .

  
  

• Transponerlos y obtener la matriz (o - donde como se indica).

  
  

Y así, este procedimiento se repetirá para cada usuario. ¿No es esta la magia de las matemáticas: usando los métodos de álgebra lineal, resolvemos problemas completamente técnicos!

Tenga en cuenta que en la práctica no solo se utilizan las matrices de codificación previa obtenidas, sino también las matrices de procesamiento posterior y la matriz de valores singulares (ver diapositivas ). Este último, por ejemplo, para equilibrar la potencia de acuerdo con el algoritmo de vertido de agua ya conocido.

Modelamos el algoritmo

Creo que no será superfluo realizar una pequeña simulación para consolidar el resultado. Para hacer esto, usaremos Python 3, a saber:

import numpy as np 

para cálculos básicos y:

 import pandas as pd 

para mostrar el resultado.

 class ZeroForcingBD: def __init__(self, H, Mrs_arr): Mr, Mt = np.shape(H) self.Mr = Mr self.Mt = Mt self.H = H self.Mrs_arr = Mrs_arr def __routines(self, H, mr, shift): # used in self.process() - See example above for illustration # inputs: # H - the whole channel matrix # mr - number of receive antennas of the i-th user # shift - how much receive antennas were considered before # outputs: # Uidx, Sigmaidx, Vhidx - SVD decomposition of the H_iP_i # d - rank of the hat H_i # Hidx - H_i (channel matrix for the i-th user) # r - rank of the H_i Hidx = H[0+shift:mr+shift,:] # H_i (channel matrix for the i-th user) r = np.linalg.matrix_rank(Hidx) # rank of the H_i del_idx = [i for i in range(0+shift, mr+shift, 1)] # row indeces of H_i in H H_hat_idx = np.delete(H, del_idx, 0) # hat H_i d = np.linalg.matrix_rank(H_hat_idx) # rank of the hat H_i U, Sigma, Vh = np.linalg.svd(H_hat_idx) # SVD Vhn = Vh[d:, :] # null-subspace of V^H Vn = np.matrix(Vhn).H # null-subspace of V Pidx = np.dot(Vn, np.matrix(Vn).H) # projection matrix Uidx, Sigmaidx, Vhidx = np.linalg.svd(np.dot(Hidx, Pidx)) # SVD of H_iP_i return Uidx, Sigmaidx, Vhidx, d, Hidx, r def process(self): # used in self.obtain_matrices() # outputs: # F - whole filtering (pre-coding) matrix (array of arrays) # D - whole demodulator (post-processing) matrix (array of arrays) # H - the whole channel matrix (array of arrays) shift = 0 H = self.H F = [] D = [] Hs = [] for mr in self.Mrs_arr: Uidx, Sigmaidx, Vhidx, d, Hidx, r = self.__routines(H, mr, shift) Vhidx1 = Vhidx[:r,:] # signal subspace Fidx = np.matrix(Vhidx1).H F.append(Fidx) D.append(Uidx) Hs.append(Hidx) shift = shift + mr return F, D, Hs def obtain_matrices(self): # used to obtain pre-coding and post-processing matrices # outputs: # FF - whole filtering (pre-coding) matrix # DD - whole demodulator (post-processing) matrix (array of arrays) F, D, Hs = self.process() FF = np.hstack(F) # Home Task: calculation of the demodulator matrices :) return FF 

Supongamos que tenemos 8 antenas transmisoras y 3 usuarios que tienen 3, 2 y 3 antenas receptoras, respectivamente:

 Mrs_arr = [3,2,3] # 1st user have 3 receive antennas, 2nd user - 2 receive antennas, 3d user - 3 receive antennas Mr = sum(Mrs_arr) # total number of the receive antennas Mt = 8 # total number of the transmitt antennas H = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2); #Rayleigh flat faded channel matrix (MrxMt) 

Inicializamos nuestra clase y aplicamos los métodos apropiados:

 BD = ZeroForcingBD(H, Mrs_arr) F, D, Hs = BD.process() FF = BD.obtain_matrices() 

Traemos a una forma legible:

 df = pd.DataFrame(np.dot(H, FF)) df[abs(df).lt(1e-14)] = 0 

Y tomemos un pequeño impulso para mayor claridad (aunque puede sin ella):

 print(pd.DataFrame(np.round(np.real(df),100))) 

Deberías obtener algo como esto:

En realidad, aquí están los bloques, aquí está y la diagonalización. Y minimizando la interferencia.

Tales cosas

Literatura

1. Spencer, Quentin H., A. Lee Swindlehurst y Martin Haardt. "Métodos de forzamiento cero para la multiplexación espacial de enlace descendente en canales MIMO multiusuario". Transacciones IEEE sobre procesamiento de señales 52.2 (2004): 461-471.
2. Martin Haard " Procesamiento de transmisión robusto para sistemas MIMO multiusuario "

PS

¡Al personal docente y a la fraternidad estudiantil de mi profesión nativa les saludo!