Permutaciones aleatorias y particiones aleatorias

Durante muchos años he estado dando cursos de combinatoria y gráficos para estudiantes de matemática e informática (¿cómo es en ruso, informáticos?), Anteriormente en la Universidad Académica y ahora en la Universidad Estatal de San Petersburgo . Nuestro programa está diseñado para que estos temas se lleven a cabo como parte de la "informática teórica" ​​(otros temas son algoritmos, complejidad, lenguajes y gramáticas). No puedo decir cuán metafísica o históricamente se justifica: sin embargo, los objetos combinatorios (gráficos, sistemas de conjuntos, permutaciones, figuras a cuadros, etc.) comenzaron a estudiarse mucho antes del advenimiento de las computadoras, y ahora este último, aunque importante, está lejos de ser la única razón de interés en el. Pero mirar a los mismos especialistas en combinatoria y ciencias de la computación teórica es sorprendentemente a menudo las mismas personas: Lovas, Alon, Semeredi, Razborov y más allá. Probablemente hay razones para esto. En mis lecciones, los campeones de la programación olímpica a menudo ofrecen soluciones muy triviales a problemas complejos (no los enumeraré, cualquiera que tenga curiosidad por ver las fuerzas de código principales). En general, creo que algunas cosas de la combinatoria pueden ser de interés para la comunidad. Habla si algo es así o no.

Le permite construir una permutación aleatoria de números del 1 al$$ $ en línea $ n $ en línea $ para que todas las permutaciones sean igualmente probables. Esto se puede hacer de muchas maneras: por ejemplo, primero seleccione al azar el primer elemento, luego del segundo restante y así sucesivamente. O puede hacer lo contrario: seleccione puntos al azar$$ $ en línea $ t_1, t_2, \ ldots, t_n $ en línea $ en el segmento$$ $ en línea $ [0,1] $ en línea $ , y ver cómo se ordenan. Reemplazando el más pequeño de los números con 1, el segundo con 2, y así sucesivamente, obtenemos una permutación aleatoria. Fácil de ver que todo$$ $ en línea $ n! $ en línea $ las permutaciones son igualmente probables. Es posible y no en el segmento.$$ $ en línea $ 0.1 $ en línea $ elegir puntos y, por ejemplo, entre números del 1 al$$ $ en línea $ n $ en línea $ . Aquí son posibles las coincidencias (para un segmento, también son posibles, pero con probabilidad cero, por lo que no nos molestan): puede tratarlas de diferentes maneras, por ejemplo, reordenando adicionalmente los números coincidentes. O tome N más grande para que la probabilidad de coincidencia sea pequeña (el caso cuando$$ $ en línea $ N = 365 $ en línea $ y$$ $ en línea $ n $ en línea $ existe el número de estudiantes en su clase, y estamos hablando de la coincidencia de dos cumpleaños.) Una variación de este método: nota aleatoria$$ $ en línea $ n $ en línea $ apunta en un cuadrado unitario y observa cómo se ordenan sus ordenadas en relación con las abscisas. Otra variación: marca en el segmento$$ $ en línea $ n-1 $ en línea $ apunte y vea cómo se ordenan las longitudes de los segmentos en los que se divide. El punto clave en estos enfoques es la independencia de las pruebas, de acuerdo con los resultados de los cuales se construye una reorganización aleatoria. Andrei Nikolaevich Kolmogorov dijo que la teoría de la probabilidad es una teoría de la medida más la independencia, y esto será confirmado por cualquiera que haya lidiado con la probabilidad.

Mostraré cómo ayuda esto, usando el ejemplo de la fórmula de ganchos para árboles :



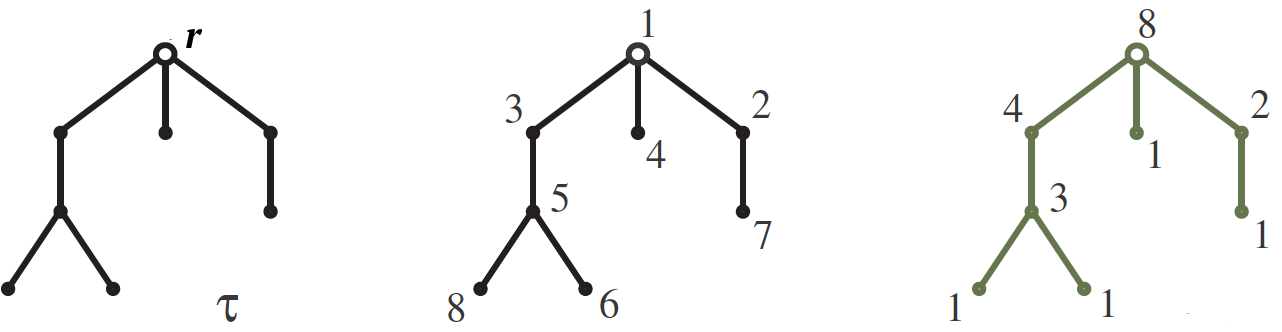
Dejar$$ $ en línea $ \ tau $ en línea $ - suspendido por la raíz$$ $ en línea $ r $ en línea $ árbol con$$ $ en línea $ n $ en línea $ picos que crecen hacia abajo como en la imagen. Nuestro objetivo es calcular el número$$ $ en línea $ S (\ tau) $ en línea $ numeración de copas de los árboles$$ $ en línea $ \ tau $ en línea $ números del 1 al$$ $ en línea $ n $ en línea $ tal que para cada borde el número en su parte superior es mayor que en la parte inferior. Uno de estos números se muestra en la imagen central. La respuesta se formula utilizando tamaños de gancho . Gancho$$ $ en línea $ H (v) $ en línea $ picos$$ $ en línea $ v $ en línea $ llamemos a un subárbol que crece a partir de este vértice, y su tamaño es simplemente el número de vértices en él. Las longitudes de gancho se escriben en la imagen de la derecha al lado de los vértices correspondientes. Entonces, el número de números es$$ $ en línea $ n! $ en línea $ dividido por el producto de los tamaños de gancho, así que para nuestro ejemplo

$$$$ display $$ S (\ tau) = \, \ frac {8!} {8 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 \ cdot 1 \ cdot 1 \ cdot 1} = 210. $$ display $ $ $

Podemos probar esa fórmula de diferentes maneras, por ejemplo, por inducción sobre el número de vértices, pero nuestra visión de las permutaciones aleatorias nos permite llevar a cabo la prueba sin ningún cálculo. Es mejor no solo por elegancia, sino también porque se generaliza bien a preguntas más sutiles sobre numeración con desigualdades prescritas, pero no sobre eso ahora. Entonces, tome n números reales diferentes y colóquelos al azar en la parte superior del árbol, cada uno con un número, todos$$ $ en línea $ n! $ en línea $ las permutaciones son igualmente probables. ¿Cuál es la probabilidad de que para cada borde, el número en el vértice superior del borde sea mayor que el número en su vértice inferior? La respuesta es:$$ $ en línea $ S (\ tau) / n! $ en línea $ , y no depende de un conjunto de números. Y si no depende, entonces consideremos los números también seleccionados al azar, por definición, en el intervalo$$ $ en línea $ [0,1] $ en línea $ . En lugar de seleccionar al azar números al principio y luego colocarlos al azar en la parte superior del árbol, simplemente podemos seleccionar aleatoriamente e independientemente un número en cada vértice: su reordenamiento será aleatorio automáticamente. De esta manera$$ $ en línea $ S (\ tau) / n! $ en línea $ esta es la probabilidad de que para números independientes aleatorios$$ $ en línea $ \ xi (v) $ en línea $ seleccionado uno para cada vértice$$ $ en línea $ v $ en línea $ madera$$ $ en línea $ \ tau $ en línea $ , todas las desigualdades de la forma$$ $ en línea $ \ xi (v)> \ xi (u) $ en línea $ para todos los bordes$$ $ en línea $ v \ a u $ en línea $ ,$$ $ en línea $ v $ en línea $ Es el vértice superior de la costilla, y$$ $ en línea $ u $ en línea $ - abajo. Formulamos estas condiciones en una forma equivalente, pero de una manera ligeramente diferente: para cada vértice$$ $ en línea $ v $ en línea $ tal evento debería ocurrir - lo designaré

$$$ en línea $ Q (v) $ en línea $ : número$$ $ en línea $ \ xi (v) $ en línea $ - el máximo entre todos los números en los vértices del subárbol de gancho$$ $ en línea $ H (v) $ en línea $ .

Tenga en cuenta que$$ $ en línea $ \ frac {1} {| H (v) |} $ en línea $ esta es la probabilidad de un evento$$ $ en línea $ Q (v) $ en línea $ . De hecho, en el gancho$$ $ en línea $ H (v) $ en línea $ está disponible$$ $ en línea $ | H (v) | $ en línea $ vértices y el número de gancho máximo se asigna a cada uno de ellos con igual probabilidad$$ $ en línea $ \ frac {1} {| H (v) |} $ en línea $ . Entonces la fórmula del gancho$$ $ en línea $ S (\ tau) / n! = \ prod_v \ frac {1} {| H (v) |} $ en línea $ se puede formular de la siguiente manera: la probabilidad de que todos los eventos ocurran a la vez$$ $ en línea $ Q (v) $ en línea $ es igual al producto de las probabilidades de estos eventos. Las razones para esto pueden ser muy diferentes, pero la primera que viene a la mente funciona aquí: estos eventos son independientes. Para entender esto, veamos, por ejemplo, un evento$$ $ en línea $ Q (r) $ en línea $ (correspondiente a la raíz). Consiste en el hecho de que el número en la raíz es mayor que todos los otros números en los vértices, y otros eventos se relacionan con comparaciones entre ellos de números escritos no en la raíz. Eso es$$ $ en línea $ Q (r) $ en línea $ con respecto al número$$ $ en línea $ \ xi (r) $ en línea $ y conjuntos de números en otros vértices, y todos los demás eventos son del orden de números en vértices distintos de la raíz. Como ya hemos discutido, "orden" y "multitud" son independientes, por lo tanto, el evento$$ $ en línea $ Q (r) $ en línea $ independiente de los demás. Bajando por el árbol, obtenemos que todos estos eventos son independientes, de donde se sigue lo requerido.

Por lo general, la fórmula para los ganchos es la fórmula para numerar no los vértices del árbol, sino las celdas del diagrama de Young. aumentando en las direcciones de los ejes de coordenadas, y los ganchos hay más ganchos que árboles. Pero esta fórmula se demostró más complicada y merece una publicación separada.

Como lo hice por cierto, no puedo evitar hablar sobre el modelo de un diagrama de Young al azar . Diagrama joven es una figura de$$ $ en línea $ n $ en línea $ unidades cuadradas, la longitud de sus filas aumenta de abajo hacia arriba y la longitud de las columnas de izquierda a derecha. Número de gráficos de área de Young$$ $ en línea $ n $ en línea $ está indicado$$ $ en línea $ p (n) $ en línea $ , esta importante función se comporta de una manera interesante e inusual: por ejemplo, crece más rápido que cualquier polinomio, pero más lento que cualquier exponente. Por lo tanto, en particular, genere un diagrama de Young aleatorio (si queremos todos los diagramas de área$$ $ en línea $ n $ en línea $ eran igualmente probables$$ $ en línea $ 1 / p (n) $ en línea $ ) no es un asunto trivial. Por ejemplo, si agrega celdas una a la vez, eligiendo un lugar para agregar al azar, diferentes gráficos tendrán diferentes probabilidades (por lo tanto, la probabilidad de un gráfico de una sola línea resulta ser igual$$ $ en línea $ 1/2 ^ {n-1} $ en línea $ .) Resulta una medida entretenida en los diagramas, pero no uniforme. El uniforme se puede obtener de la siguiente manera. Toma el numero$$ $ en línea $ t \ in (0,1) $ en línea $ , para nuestros propósitos, los números en el área son los más adecuados$$ $ en línea $ 1- \ mathrm {const} / \ sqrt {n} $ en línea $ . Para cada$$ $ en línea $ k = 1,2, \ ldots $ en línea $
considerar la distribución geométrica en enteros no negativos con media$$ $ en línea $ t ^ k $ en línea $ (es decir, probabilidad del número$$ $ en línea $ m = 0,1, \ ldots $ en línea $ es igual a$$ $ en línea $ t ^ {km} (1-t ^ k) $ en línea $ ) Elegimos según ella una variable aleatoria$$ $ en línea $ m_k $ en línea $ (Hay muchas formas de organizar esto). En general$$ $ en línea $ k $ en línea $ muy probablemente 0. Veamos el diagrama de Young en el que$$ $ en línea $ m_k $ en línea $ las filas son longitud$$ $ en línea $ k $ en línea $ en cada$$ $ en línea $ k = 1,2, \ ldots $ en línea $ . Lo llamo el método de envío porque el área total es a veces igual a$$ $ en línea $ n $ en línea $ . Si no es igual, repite el experimento. En realidad igual$$ $ en línea $ n $ en línea $ ella lo suficientemente a menudo si elige inteligentemente$$ $ en línea $ t \ in (0,1) $ en línea $ . Invito al lector a probar de forma independiente que todos los diagramas de un área dada son igualmente probables y estimar el número de pasos.