29 de marzo de 2019: Michael Trott, investigador principal
Entrada
En el llamado "nuevo SI" - una
versión actualizada del Sistema Internacional de Unidades , que determinará siete unidades básicas de medida (segundo, metro, kilogramo, amperio, kelvin, mole y candela) y que entrará en vigor el 20 de mayo de 2019, todas las unidades SI serán determinado a través de los valores exactos de las constantes físicas fundamentales. Como resultado, todas las unidades SI anteriores (Newton, Volt, Ohm, Pascal, etc.) se expresarán en términos de constantes fundamentales. (Finalmente, la física fundamental controlará literalmente nuestra vida diaria ☺)
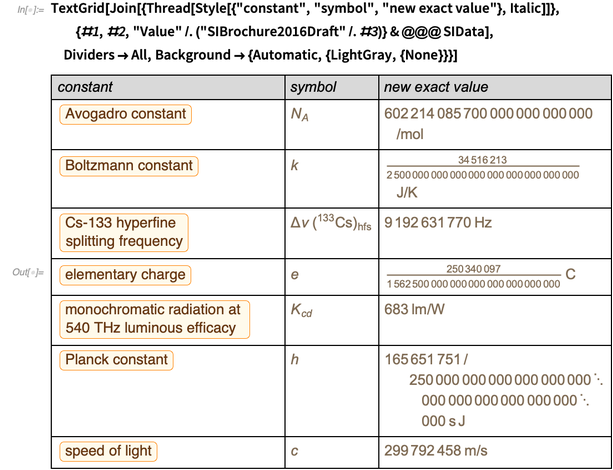
La siguiente tabla muestra cómo cambiará todo desde el lunes 20 de mayo por la noche hasta el martes por la mañana del 21 de mayo de este año.
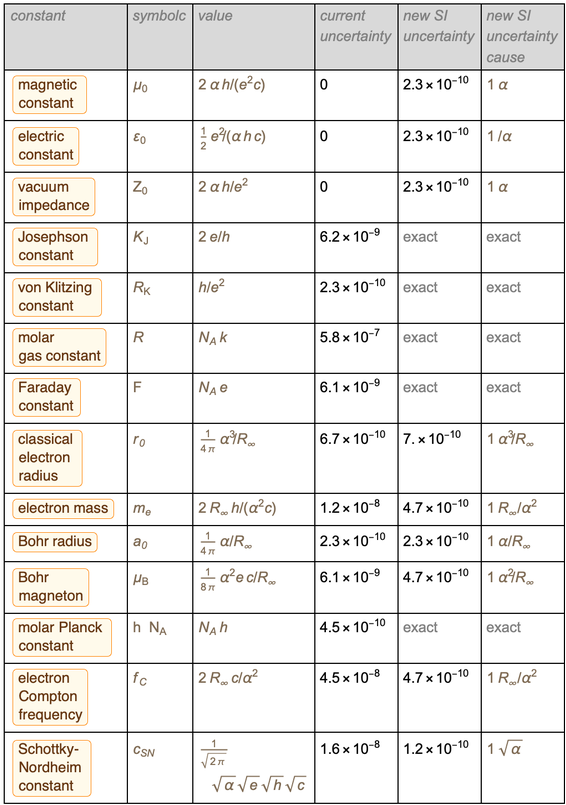
El objetivo de este blog es calcular los datos de esta tabla. Entonces, comencemos con una breve descripción de lo que cambiará en el nuevo SI.
Además del conocido valor exacto de la velocidad de la luz, en cuatro semanas otras cuatro constantes físicas: la constante de Planck, la constante de Boltzmann, la constante de Avogadro y la constante de Millikan (a menudo llamada carga eléctrica elemental) tendrán valores exactos. La decisión sobre este cambio se tomó internacionalmente en noviembre del año pasado (escribí sobre esto en mi último
blog)
A continuación se muestra un fragmento de la página 12 del borrador actual del
folleto de SI .
Tenga en cuenta que en estas definiciones, los números decimales se entienden como números decimales exactos, no, digamos, números de máquina en una computadora que tienen precisión finita y no son números exactos. La frecuencia de transición en la estructura superfina dividida de Cs-133, la velocidad de la luz y la "eficiencia de la luz" ya tienen valores exactos en la actualidad.
El mundo discute cambios futuros
Este cambio tendrá algunas consecuencias interesantes para otras constantes físicas: algunas constantes que se miden actualmente y tienen errores se volverán precisas, y algunas constantes que actualmente son precisas tendrán valores aproximados con errores finitos en el futuro . Estos cambios son inevitables para garantizar la coherencia general del sistema.
El primer número
de este año
de Física del mundo abordó este tema en una
carta al editor de William Hough; el escribió:
Con la fijación de carga en el electrón ( e ) y la constante de Planck ( h ), todas las unidades físicas ahora están "inmortalizadas en piedra", lo cual es muy agradable. Pero eso plantea una pregunta incómoda. Estructura fina constante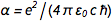 
donde c es la velocidad de la luz y 
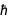es 
. De ecuaciones familiares 
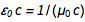y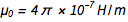 
rápidamente encontramos que 
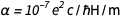. Esto, por supuesto, es un número puro con una cantidad adimensional, y ahora se fija para siempre como igual a 1 / 137.13601, que está muy cerca del valor aceptado. Esto no es sorprendente, ya que este último valor se usaría en los nuevos valores acordados para e y ℏ . Pero la naturaleza tiene su propio valor, desconocido para nosotros en la actualidad, que, debido a esto, está inmortalizado en diamante. Podemos ser perdonados por insinuar que sabemos mejor que la naturaleza. Pero, ¿qué pasa si la futura teoría del universo se acepta y da el significado exacto? 
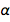¿Cuál es significativamente diferente del valor aceptado? ¿Podría pasar esto? Ha habido intentos de encontrar un valor teórico para α , pero incluyen la electrodinámica cuántica amenazante y controvertida.
El problema es que en el nuevo sistema SI ambos
y
ahora tendrá valores inexactos con algún error. En este blog, utilizaremos Wolfram Language y su conocimiento de unidades físicas y constantes para ver cómo estas y otras constantes físicas ganan (o pierden) errores, y por qué es una consecuencia matemática de la definición de unidades básicas.
Una breve descripción de los ingredientes relevantes de Wolfram Language
Wolfram Language es un medio único para realizar experimentos numéricos y cálculos simbólicos, identificando posibles consecuencias. Además de las capacidades informáticas generales, aquí son muy útiles tres componentes del sistema:
1) Unidades de Wolfram Language y estructura de cantidades físicas.
Las unidades clásicas (como metros, pies, etc.) se pueden usar en cálculos y visualizaciones. Y, por supuesto, en la conversión de unidades de medida.
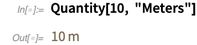
La conversión a unidades estadounidenses normales da como resultado una fracción (¡en lugar de un valor aproximado del número real!) Debido a las proporciones bien definidas de las dos unidades.
A los físicos (especialmente) les gusta usar unidades "naturales". A menudo, estas unidades naturales son simplemente constantes físicas o combinaciones de las mismas. Por ejemplo, la velocidad de la luz (aquí se usa la entrada de lenguaje natural).
Expresado en unidades SI (dado que se trata de velocidad y se requieren unidades en metros y segundos), la velocidad de la luz tiene un valor preciso.
Por otro lado, la constante de Planck no tiene actualmente un valor exacto. Por lo tanto, su valor, expresado en unidades base SI, es un número decimal aproximado.
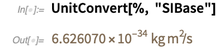
Tenga en cuenta que la precisión de 6.626070 ... refleja el número de números conocidos.
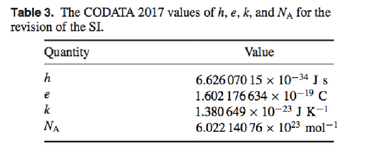
Este es el último valor recomendado para la constante de Planck publicada en
CODATA 2017 en preparación para el refinamiento de las constantes. A continuación se muestra la tabla correspondiente:
Las constantes físicas (o combinaciones de las mismas) que unen dos cantidades físicas a menudo se pueden usar como unidades naturales. Los ejemplos más simples serían la medición de la velocidad en términos de la velocidad de la luz o el par microscópico en términos de
ℏ . O la energía se puede medir en términos de masa con un factor implícito
. La función
DimensionalCombinations puede usarse para buscar combinaciones de constantes físicas que le permitan relacionar dos cantidades físicas dadas. Por ejemplo, se pueden construir las siguientes relaciones entre masa y energía:
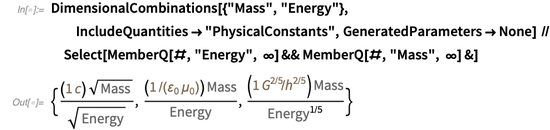
La primera igualdad refleja la famosa fórmula de Einstein
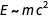
, el segundo es el equivalente de la primera relación, y el tercero - (dimensionalmente) afirma que
.
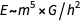
2) La clase de entidad "
PhysicalConstant " recientemente agregada a la base de
conocimiento de Wolfram .
Las funciones y los objetos en Wolfram Language "nacen computacionalmente", es decir, están listos para usar en computación. Pero para describir y simular el mundo real, necesita datos sobre el mundo real. La estructura de la entidad es una forma conveniente y totalmente integrada de obtener dichos datos. A continuación se presentan algunos datos sobre el electrón, el protón y el neutrón.
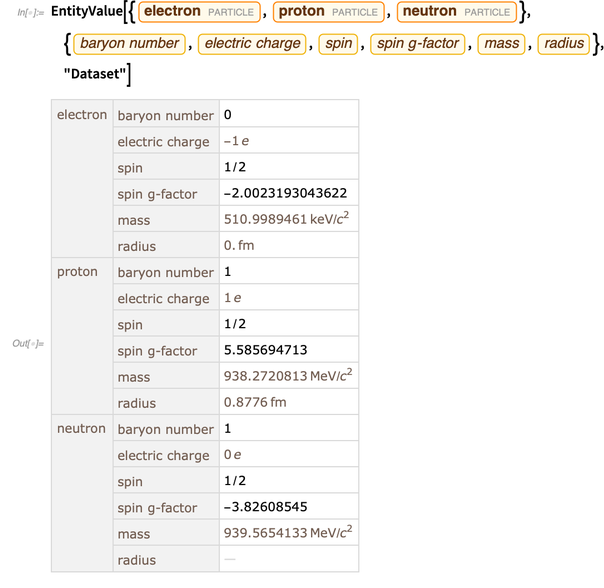
Una de las nuevas unidades de entidad son las constantes físicas. Actualmente, la Base de conocimiento contiene más de 250 constantes físicas.
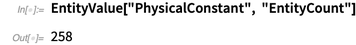
A continuación hay una docena de ejemplos seleccionados al azar. Además, sin una definición clara de qué constantes son constantes físicas, masas de partículas fundamentales, parámetros de Lagrange del modelo estándar, etc. Por conveniencia, la lista también contiene
constantes astronómicas de acuerdo con el Almanaque Astronómico.
La mayoría de las constantes físicas fundamentales se denominaron constantes de clase C en el famoso
trabajo de Jean-Marc Levy-Leblond. Las siguientes son constantes de las clases C y B.
Tomemos, por ejemplo, la unidad natural de tiempo, el tiempo de Planck. Las
funciones ToEntity y
FromEntity facilitan el ir y venir entre constantes físicas como unidades y constantes físicas como entidades. A continuación se muestra una entidad correspondiente a una unidad de tiempo de Planck.
La base de conocimiento tiene mucha metainformación sobre él, por ejemplo, sus valores en las últimas listas de CODATA.
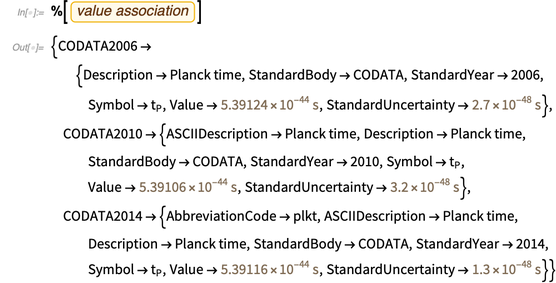
La última conclusión, que contiene significado y error, nos lleva a la tercera función importante, que será útil más adelante:
3) Introducción de la función
Around [] en la versión 12 del Wolfram Language. La función
Alrededor [] proporciona un valor inexacto, que indica el valor promedio y el error. El modelo aritmético
Around [] se basa en la
GUM (Guía para expresar el error de medición), que no debe confundirse con el cálculo Leibniz Plus-Minus. Aquí hay un valor con un error.
El aspecto más importante y útil de la computación con valores que tienen errores es que tienen en cuenta las correlaciones. El uso ingenuo de tales valores en números o intervalos aritméticos puede subestimar o sobreestimar el error resultante.
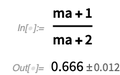
A continuación vemos que la función
AroundReplace [] tiene en cuenta la correlación.
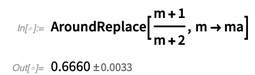
Volver a la carta al editor.
Ahora usemos estos tres componentes y la carta más detallada de William Hough al editor.
En los valores aproximados actuales para
e y
ℏ , estos dos valores para la constante de estructura fina son consistentes dentro de los límites de sus errores. La primera es la expresión de la carta al editor, y la segunda es la cantidad (
Cantidad []), que representa la constante de estructura fina.
Cada pocos años, CODATA publica valores oficiales de constantes fundamentales (ver
constantes de estructura fina ); Como dije, los valores utilizados en Wolfram Language son los últimos valores CODATA y el error final se refleja en la precisión del número.
Tenga en cuenta que la constante de estructura fina medida directamente es ligeramente más precisa que la que expresa la constante de estructura fina a través de otras constantes.
Si usamos los próximos valores exactos de
e y
ℏ ,
y usamos el valor exacto actual
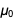
, obtenemos el siguiente valor exacto para la estructura fina constante en la forma
.
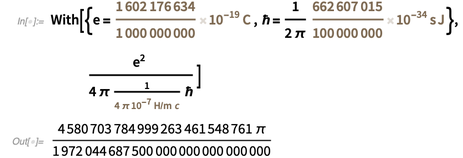
Es poco probable que el Señor, que ni siquiera
juega a los dados , elija ese número por el valor
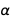
en nuestro universo Esto significa que mientras
e y
ℏ están fijos en el nuevo SI, los valores exactos actuales
y
inevitablemente debe estar "desacoplado" (ver también el
artículo de Goldfarb sobre la cantidad
nuevo SI). (Volveremos a por qué
y
pronto se volverá inexacto)
Esto significa que después del 20 de mayo de este año, estos resultados serán diferentes de los que se detallan a continuación.
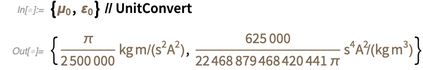
(En una nota breve, la clase de entidad "
PhysicalConstant " también tiene valores estimados para constantes, como la constante de estructura fina):
Ahora, aparte del argumento teológico sobre la forma exacta de la constante de estructura fina, desde un punto de vista físico, ¿por qué?
y
debe ser inexacto? Como argumento de probabilidad, consideremos
. Uno de los resultados más destacados es la ley de Coulomb.
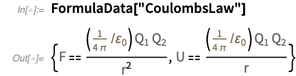
En el
sistema SI
existente , los amperios tienen una definición "exacta":
Un amperio es esa corriente continua que, si se apoya en dos conductores paralelos de longitud infinita con una ligera sección transversal redonda y se coloca a una distancia de 1 metro en el vacío, creará una fuerza entre estos conductores igual a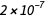 
Newton por metro de longitud. Esta definición utiliza cantidades puramente mecánicas Newton y metro (es decir, después de la expansión, este es un segundo, metro y kilogramo). No se establece ninguna relación con la carga del electrón, y en el sistema SI existente, la carga elemental es una cantidad medida experimentalmente.
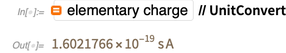
Y este valor medido experimentalmente ha cambiado con los años, volviéndose más preciso.
La fuerza en el lado izquierdo de la ley de Coulomb (expresada en Newtons) contiene la unidad básica de kilogramo que, después de que el valor de la constante de Planck se vuelve constante, también se puede definir con precisión. Dado que no hay razón para creer que todas las leyes de la naturaleza pueden expresarse en números racionales finitos, la única "parte móvil" posible en la ley de Coulomb será
. Se debe determinar su valor numérico, y hará que los lados izquierdo y derecho de la ley de Coulomb coincidan.
Desde un punto de vista más fundamental de la física, la constante de estructura fina es la constante de interacción, que determina la fuerza de las interacciones electromagnéticas. Y, tal vez algún día, la física pueda calcular el valor de la constante de estructura fina, pero aún estamos lejos de esto. Simplemente elegir definiciones de unidad no puede arreglar el valor
.
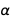
Son ambos realmente
y
no se fija, o ¿es posible mantener uno de ellos exacto? Debido a la velocidad de luz ya precisa y la relación
si uno de
o
precisa, la otra también debe ser precisa. Sabemos que al menos uno debe ser no comprometido, por lo que se deduce que ambos deben ser no comprometidos.
Los valores ahora dados por la constante de Planck, la constante de Boltzmann, la constante de Avogadro y la carga elemental no son arbitrarios ni están completamente definidos. Se determinan hasta aproximadamente ocho caracteres, por lo que las unidades de medida que determinan después del 20 de mayo corresponden al "tamaño" de las unidades que determinan antes del 20 de mayo. Pero los números en la esquina inferior derecha no están definidos. Por lo tanto, el valor del valor exacto futuro de la carga elemental puede ser
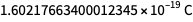
pero no
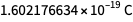
. La maquinilla de afeitar y la racionalidad de Occam nos permiten usar
.
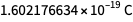
En un nivel más técnico, la sustitución en el cálculo anterior fue que a través del término
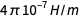
en la fórmula
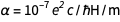amp se usó antes de la redefinición (recuerde
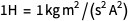
), pero también se utilizó el valor exacto de la carga elemental, lo que significa la definición del amperio después de la redefinición. Y siempre necesitamos permanecer en un sistema de unidades.
Cálculo de la tabla de formulario optimizada para errores
Entonces, surge la pregunta natural: ¿cuáles deberían ser estos significados "no fijados"? En mi último blog, creé manualmente un nuevo valor
. Lo que se puede hacer manualmente se puede hacer usando un programa de computadora, así que implementemos un pequeño programa que calcule la forma optimizada de error de derivadas de constantes físicas. En un enfoque orientado al futuro, una clase de entidad de siete constantes que define un nuevo SI ya está disponible.
A continuación hay constantes que tendrán un valor exacto en el nuevo SI.
Los valores actuales de estas constantes junto con su error (calculado usando la función
Alrededor []) tienen la forma:
Usando la clase de entidad "
PhysicalConstant " podemos obtener valores nuevos y próximos de cantidades físicas. Tenga en cuenta que, como en todos los lenguajes de computadora, los enteros exactos y los números racionales son enteros explícitos o números racionales (pero no decimales).
Muchas constantes físicas pueden relacionarse mediante ecuaciones dadas por teorías físicas de diversos campos de la física. En el futuro, queremos limitarnos a la teoría de los fenómenos electromagnéticos fundamentales, en la que el error de las constantes se reducirá al error de la constante de estructura fina.
y constante de Rydberg
. Si incluimos, por ejemplo, los fenómenos gravitacionales, tendríamos que usar la constante gravitacional G, que se mide de forma independiente, aunque tiene un error muy grande (es por eso que la NSF tuvo el llamado "
Gran desafío G ").
Además, nos restringimos a cantidades eléctricas, magnéticas y de masa, cuyos errores se reducen a unidades.
y
.
A continuación, utilizamos la nueva función
Alrededor para expresar valores con los errores correspondientes.
y
.
Actualmente, según CODATA 2014, el error relativo para
es sobre
y para
acerca de
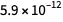
. Como puede ver, el error para
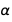
más que para
.
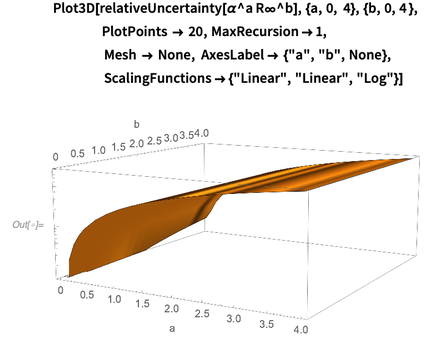
A continuación se muestra un gráfico de error relativo log-base-10
como funciones
ay b . Obviamente, para pequeños grados, el error relativo del producto depende débilmente de los exponentes
a y
b . Este gráfico muestra que la dependencia del error
domina en relación a
a (exponente de estructura fina). Esta observación se explica por el hecho de que el error de la constante de Rydberg es 50 veces menor que el error de la constante de estructura fina.
Para calcular los errores de varias constantes en el nuevo SI, utilizaremos los siguientes pasos:
• Recuperar representaciones equivalentes para constantes físicas accesibles desde la clase de entidad
PhysicalConstant .
Estas igualdades idénticas entre las constantes físicas son las leyes de la física y, como tales, deben preservarse tanto en el antiguo como en el nuevo SI.
• Piense en las fórmulas como un conjunto de igualdades algebraicas a las que se pueden aplicar varios métodos de exclusión para expresar una constante a través de una combinación de siete constantes básicas del nuevo SI, así como constantes de estructura fina
y constantes de Rydberg
.
Estas son las nueve constantes básicas que permitimos aplicar en las definiciones de cada nueva constante considerada. (Técnicamente, hay 10 constantes en la lista, pero debido a la simple relación de escala entre
h y
ℏ , en realidad hay nueve constantes "diferentes" en esta lista).
La clase de entidad "
PhysicalConstant " contiene mucha información sobre las relaciones entre las constantes físicas. Por ejemplo, aquí hay formas equivalentes de cuatro constantes que se están midiendo actualmente y que pronto se identificarán con valores precisos.
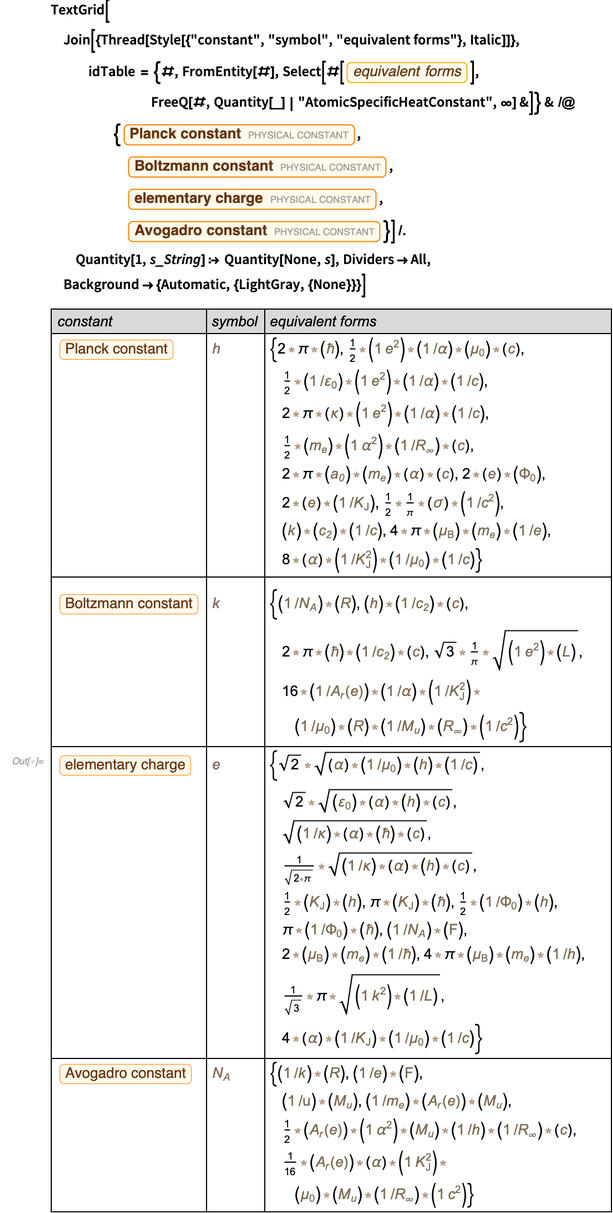
Dentro de la precisión de los valores medidos, todos estos elementos unitarios funcionan ahora. Aquí hay una comprobación numérica rápida de formas alternativas de la constante de Planck. Pero el valor numérico específico, especialmente el error, depende de la forma real de presentación.
Around [], .
. .
, . , ? , , , , , .
, , ( ,
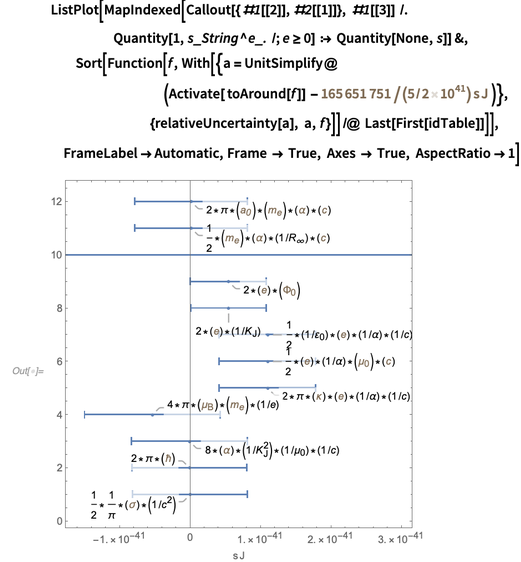
Entidad [" PhysicalConstant",. ] y en Cantidad [ 1 ,. ] son equiparados). La razón por la que usamos entidades, en lugar de cantidades en cálculos posteriores, es doble: en primer lugar, las entidades son representaciones convenientes y fáciles de leer; y en segundo lugar, las funciones algebraicas (como GroebnerBasis ) no penetran cantidades para determinar la naturaleza de su primer argumento.
Luego hacemos todas las identidades polinomiales. El último paso significa: (1) restar el lado izquierdo del lado derecho; y (2) que ya no aparecen poderes fraccionales (por ejemplo, raíces cuadradas) de constantes. Realizamos dicha conversión a un polinomio buscando todos los exponentes fraccionarios y encontrando el MCM (factor común más pequeño) de todos sus denominadores.
A continuación se muestra una de las ecuaciones anteriores que contiene constantes con una potencia fraccionaria.
Después de la polinomialización, llegamos a polinomios de varias variables en las tres constantes presentes. Estos polinomios deben ser eliminados.
La siguiente tabla muestra cómo se aplica la función
toPolynomial a las formas equivalentes mostradas anteriormente para una carga elemental. Después de la canonización de ℏ en
, algunos de los polinomios resultantes se vuelven idénticos.
Ahora, en base a las constantes físicas disponibles (sin las constantes utilizadas en la definición del nuevo SI), obtenemos suficientes formas equivalentes para crear un conjunto de ecuaciones.
A continuación se muestra una lista de las ecuaciones polinómicas obtenidas para la expresión de una carga elemental.
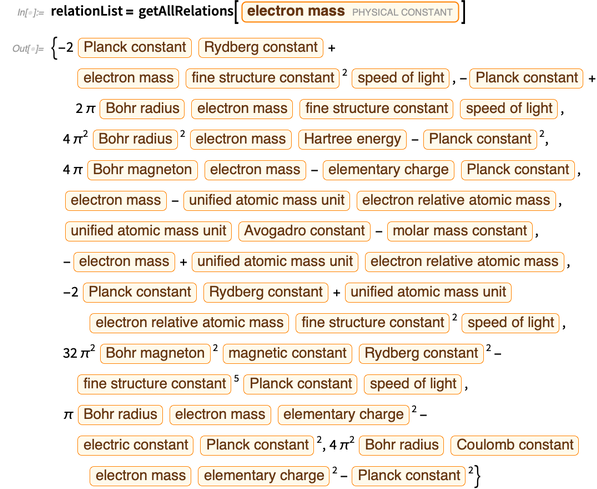
Expresamos todos los errores a través de los errores.
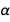
y
. Solo estas dos constantes son suficientes para expresar el error de muchas constantes físicas. Y dado que sus errores son independientes entre sí, y dado que los errores son bastante pequeños, estas dos constantes bastante conocidas son las más adecuadas para expresar una nueva versión optimizada (en el sentido de los errores) de muchas constantes físicas. Y, por supuesto, permitimos las siete constantes exactas del nuevo SI; Como son cantidades precisas, su presencia no cambiará el error.
El trabajo principal sobre la expresión de una constante dada en términos de constantes SI y
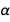
y
será implementado por la función
GroebnerBasis . Establecer el
parámetro MonomialOrder -> ElventionOrder es un paso crítico que elimina todas las cantidades físicas "innecesarias", dejando una ecuación polinómica con constantes definidas con precisión y (si es necesario) estructura fina y constantes de Rydberg.
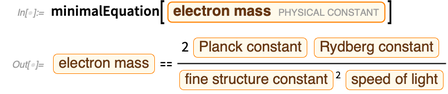
Al eliminar las constantes unidas por la masa del electrón, obtenemos
.
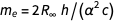
El error de esta expresión surge del término
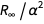
. Podemos definir una función que elimine un miembro
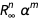
causando un error.
Para una representación más compacta, podemos definir una función que devuelva una forma equivalente, así como errores antiguos y nuevos, en forma de una cadena.
Terminamos el blog presentando una tabla de errores antiguos y nuevos para más de una docena de constantes físicas. Esta lista se selecciona como un ejemplo representativo; otras constantes pueden procesarse de manera similar (esto puede requerir la adición de constantes imprecisas adicionales para la conservación, como la constante gravitacional o los parámetros del modelo estándar).
La combinación de las filas en una tabla proporciona el siguiente resultado para la representación óptima de estas constantes en el nuevo sistema de unidades SI.
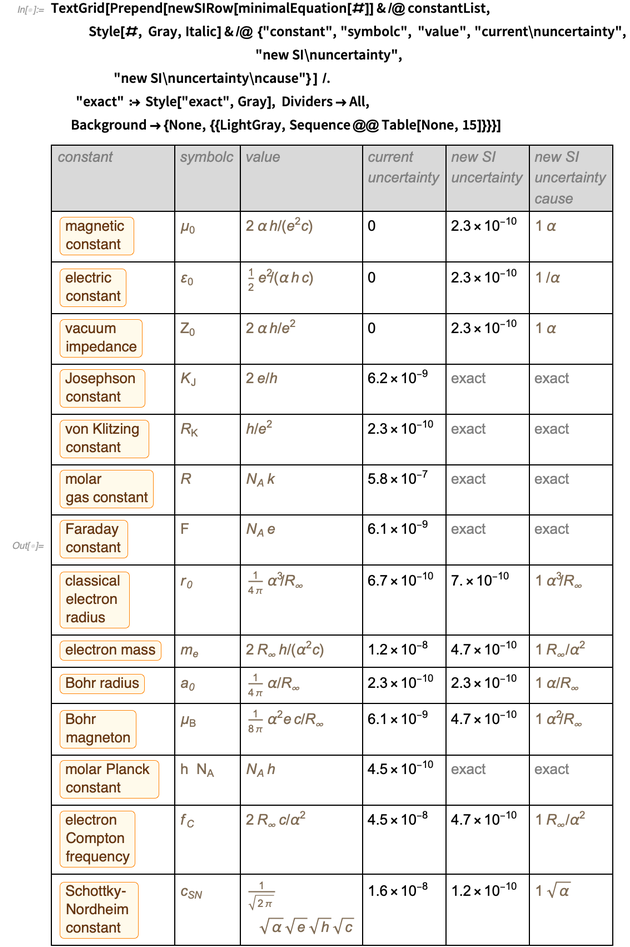
Era una tabla que teníamos la intención de mostrar, y lo logramos. Presta atención a la apariencia.
en el numerador y denominador
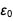
y
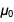
para que después de la reducción el resultado
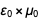
se convierte
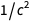
. Se puede encontrar una lista similar en la parte inferior de la página de Wikipedia sobre la
redefinición de unidades SI .
Ahora podemos esperar con calma el
Día Mundial de la Metrología 2019 para un mundo fundamentalmente mejor, descrito a través de constantes fundamentales.
Descargue el blog
Wolfram Notebook .
Sistema temporal gratuito de Wolfram MathematicaTiene una pregunta Contacto info-russia@wolfram.com