🤱🏾 🧗🏾 👩 Análisis Wavelet Parte 1 🤽🏼 🚣🏿 👩🏻‍🔧

Introduccion

Considere la transformación de wavelet discreta (DWT) implementada en la biblioteca PyWavelets PyWavelets 1.0.3 . PyWavelets es un software gratuito de código abierto lanzado bajo la licencia MIT.

Al procesar datos en una computadora, se puede realizar una versión discretizada de la transformada wavelet continua, cuyos conceptos básicos se describen en mi artículo anterior. Sin embargo, especificar valores discretos de los parámetros (a, b) de wavelets con un paso arbitrario Δa y Δb requiere una gran cantidad de cálculos.

Además, el resultado es un número excesivo de coeficientes, que supera con creces el número de muestras de la señal original, que no es necesario para su reconstrucción.

La transformada de wavelet discreta (DWT) implementada en la biblioteca PyWavelets proporciona suficiente información tanto para el análisis de señal como para su síntesis, a la vez que es económica en términos del número de operaciones y la memoria requerida.

Cuándo usar la transformada wavelet en lugar de la transformada de Fourier

La transformada de Fourier funcionará muy bien cuando el espectro de frecuencia sea estacionario. En este caso, las frecuencias presentes en la señal son independientes del tiempo, y la señal contiene las frecuencias xHz que están presentes en cualquier parte de la señal. Cuanto más inestable sea la señal, peores serán los resultados. Este es un problema, ya que la mayoría de las señales que vemos en la vida real son inestables en la naturaleza.

La transformada de Fourier tiene alta resolución en el dominio de la frecuencia, pero resolución cero en el dominio del tiempo. Mostramos esto en los siguientes dos ejemplos.

Listado

import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt # 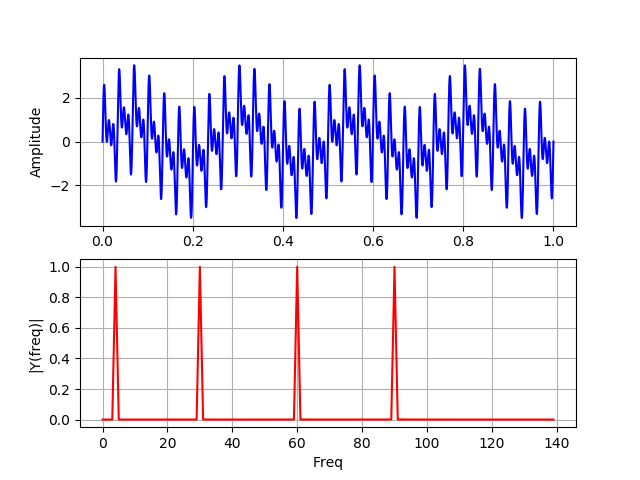sampling rate, Fs = 0,1 MHz n = len(y) # length of the signal k = np.arange(n) T = n / Fs frq = k / T # two sides frequency range frq = frq[range(n // 2)] # one side frequency range Y = fftpack.fft(y) / n # fft computing and normalization Y = Y[range(n // 2)] / max(Y[range(n // 2)]) # plotting the data subplot(2, 1, 1) plot(k/N , y, 'b') ylabel('Amplitude') grid() # plotting the spectrum subplot(2, 1, 2) plot(frq[0:140], abs(Y[0:140]), 'r') xlabel('Freq') plt.ylabel('|Y(freq)|') grid() y= y1a + y2a + y3a + y4a spectrum_wavelet(y) show()

En este gráfico, las cuatro frecuencias están presentes en la señal durante todo el tiempo de su operación.

Listado

 import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt # 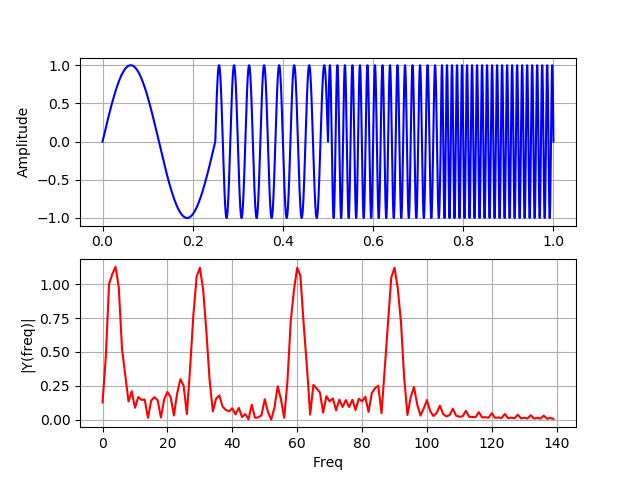sampling rate, Fs = 0,1 MHz n = len(y) # length of the signal k = np.arange(n) T = n / Fs frq = k / T # two sides frequency range frq = frq[range(n // 2)] # one side frequency range Y = fftpack.fft(y) / n # fft computing and normalization Y = Y[range(n // 2)] / max(Y[range(n // 2)]) # plotting the data subplot(2, 1, 1) plot(k/N , y, 'b') ylabel('Amplitude') grid() # plotting the spectrum subplot(2, 1, 2) plot(frq[0:140], abs(Y[0:140]), 'r') xlabel('Freq') plt.ylabel('|Y(freq)|') grid() y = np.concatenate([y1b, y2b, y3b, y4b]) spectrum_wavelet(y) show()

En este gráfico, las señales no se superponen en el tiempo, los lóbulos laterales se deben a una brecha entre cuatro frecuencias diferentes.

Para espectros de dos frecuencias que contienen exactamente los mismos cuatro picos, la transformada de Fourier no puede determinar dónde están presentes estas frecuencias en la señal. El mejor enfoque para analizar señales con un espectro de frecuencia dinámico es la transformación wavelet.

Las principales propiedades de las wavelets.

La elección del tipo y, por lo tanto, las propiedades de la wavelet, depende de la tarea de análisis, por ejemplo, para determinar los valores efectivos de las corrientes en la industria de la energía eléctrica, las formas de onda de orden superior de Ingrid Daubechies proporcionan una mayor precisión. Las propiedades Wavelet se pueden obtener utilizando la función pywt.DiscreteContinuousWavelet () en la siguiente lista:

Listado

 import pywt from pylab import * from numpy import * discrete_wavelets = ['db5', 'sym5', 'coif5', 'haar'] print('discrete_wavelets-%s'%discrete_wavelets ) st='db20' wavelet = pywt.DiscreteContinuousWavelet(st) print(wavelet) i=1 phi, psi, x = wavelet.wavefun(level=i) subplot(2, 1, 1) title("   -  -%s"%st) plot(x,psi,linewidth=2, label='level=%s'%i) grid() legend(loc='best') subplot(2, 1, 2) title("  - -%s"%st) plt.plot(x,phi,linewidth=2, label='level=%s'%i) legend(loc='best') grid() show()

Obtenemos:

discrete_wavelets - ['db5', 'sym5', 'coif5', 'haar']

 Wavelet db20 Family name: Daubechies Short name: db Filters length: 40 Orthogonal: True Biorthogonal: True Symmetry: asymmetric DWT: True CWT: False

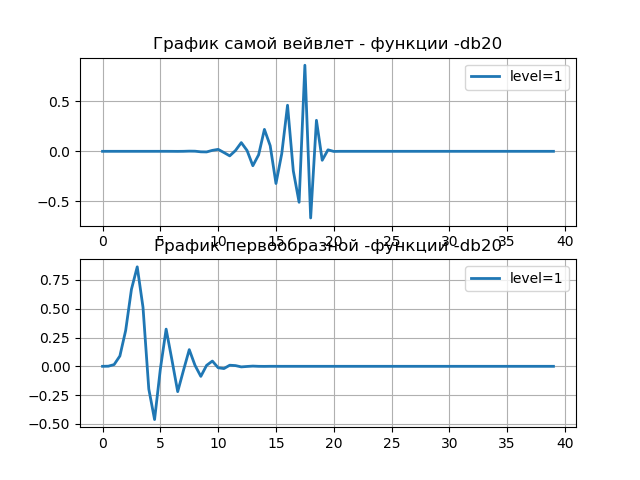
En varios casos prácticos, existe la necesidad de obtener información sobre la frecuencia central de la onda psi, una función que se utiliza, por ejemplo, en el análisis de ondas de señales para detectar defectos en los engranajes:

 import pywt f=pywt.central_frequency('haar', precision=8 ) print(f) #  : scale=1 f1=pywt.scale2frequency('haar',scale) print(f1)

 0.9961089494163424 0.9961089494163424

Usando la frecuencia central

f_{c}

$f_ {c}$ wavelet materna y factor de escala "a" pueden convertir escalas a pseudo frecuencias

f_{a}

$f_ {a}$ usando la ecuación:

f_{a} = f r a c f_{c} a

$f_ {a} = \ frac {f_ {c}} {a}$

Modos de extensión de señal

Antes de calcular la transformada de wavelet discreta utilizando bancos de filtros , es necesario alargar la señal . Dependiendo del método de extrapolación, pueden ocurrir artefactos significativos en los límites de la señal, lo que conduce a imprecisiones en la transformación DWT.

PyWavelets proporciona varias técnicas de extrapolación de señal que pueden usarse para minimizar este efecto negativo. Para demostrar tales métodos, use la siguiente lista:

Listado de demostración de métodos de extensión de señal

 import numpy as np from matplotlib import pyplot as plt from pywt._doc_utils import boundary_mode_subplot # synthetic test signal x = 5 - np.linspace(-1.9, 1.1, 9)**2 # Create a figure with one subplots per boundary mode fig, axes = plt.subplots(3, 3, figsize=(10, 6)) plt.subplots_adjust(hspace=0.5) axes = axes.ravel() boundary_mode_subplot(x, 'symmetric', axes[0], symw=False) boundary_mode_subplot(x, 'reflect', axes[1], symw=True) boundary_mode_subplot(x, 'periodic', axes[2], symw=False) boundary_mode_subplot(x, 'antisymmetric', axes[3], symw=False) boundary_mode_subplot(x, 'antireflect', axes[4], symw=True) boundary_mode_subplot(x, 'periodization', axes[5], symw=False) boundary_mode_subplot(x, 'smooth', axes[6], symw=False) boundary_mode_subplot(x, 'constant', axes[7], symw=False) boundary_mode_subplot(x, 'zeros', axes[8], symw=False) plt.show()

Los gráficos muestran cómo una señal corta (roja) se expande (negra) más allá de su longitud original.

Transformación discreta de wavelets

Para demostrar DWT, utilizaremos una señal con un espectro de frecuencia dinámico, que aumenta con el tiempo. El comienzo de la señal contiene valores de baja frecuencia, y el final de la señal contiene frecuencias del rango de onda corta. Esto nos permite determinar fácilmente qué parte del espectro de frecuencia se filtra simplemente mirando el eje de tiempo:

Listado

 from pylab import * from numpy import* x = linspace(0, 1, num=2048) chirp_signal = sin(250 * pi * x**2) fig, ax = subplots(figsize=(6,1)) ax.set_title("     ") ax.plot(chirp_signal) show()

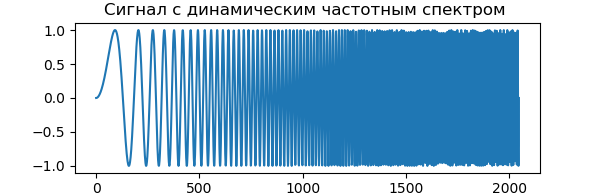
La transformada wavelet discreta en PyWavelets 1.0.3 es la función pywt.dwt (), que calcula los coeficientes aproximados cA y los coeficientes detallados cD de la transformada wavelet de primer nivel de la señal especificada por el vector:

Listado de transformación de nivel uno

 import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-1') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-1') grid() legend(loc='best') show()

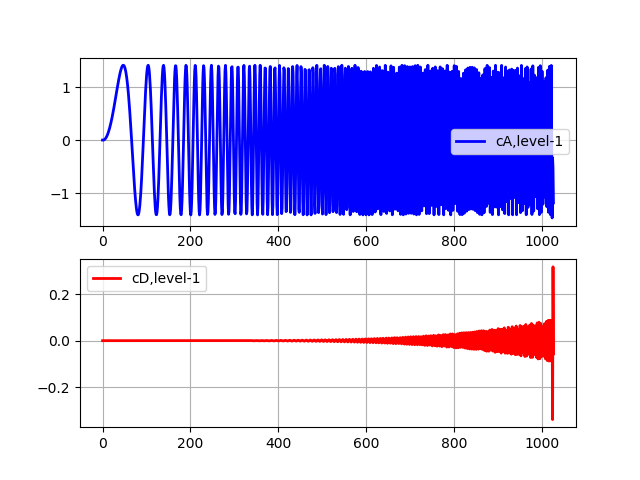
Listado de nivel 5 de transformación

 import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()

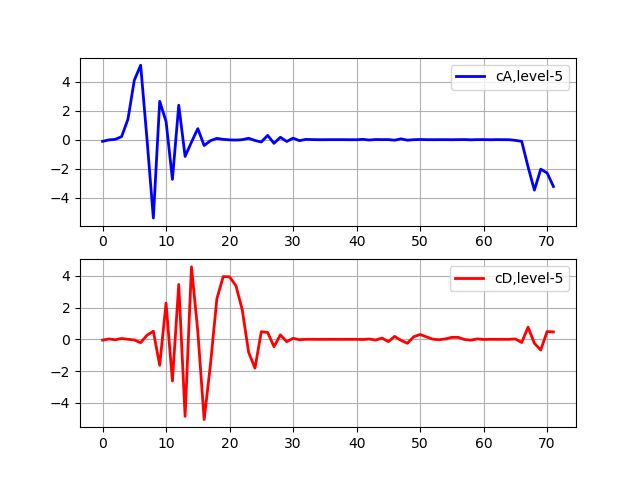
Los coeficientes de aproximación (cA) representan la salida del filtro de paso bajo (filtro de promedio) DWT. Los coeficientes de detalle (cD) representan la salida del filtro de paso alto (filtro diferencial) DWT.

Puede usar la función pywt.wavedec () para calcular inmediatamente los coeficientes de nivel superior. Esta función toma la señal y el nivel de entrada como entrada y devuelve un conjunto de coeficientes de aproximación (enésimo nivel) yn conjuntos de coeficientes de detalle (del 1 al enésimo nivel). Aquí hay un ejemplo para el quinto nivel:

 from pywt import wavedec from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=5) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()

Como resultado, obtenemos los mismos gráficos que en el ejemplo anterior. Los coeficientes cA y cD se pueden obtener por separado:

Para cA:

 import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('a', data, 'db20', mode='symmetric', level=1)

Para cD:

 import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('d', data, 'db20', mode='symmetric', level=1)

Banco de filtros

Algunos de los problemas relacionados con los niveles de conversión se discutieron en la sección anterior. Sin embargo, DWT siempre se implementa como un banco de filtros en forma de cascada de filtros de paso alto y paso bajo. Los bancos de filtros son una forma muy efectiva de dividir una señal en múltiples subbandas de frecuencia.

En la primera etapa con una escala pequeña, analizando el comportamiento de alta frecuencia de la señal. En la segunda etapa, la escala aumenta con un factor de dos (la frecuencia disminuye con un factor de dos), y analizamos el comportamiento de aproximadamente la mitad de la frecuencia máxima. En la tercera etapa, el factor de escala es cuatro, y analizamos el comportamiento de la frecuencia de aproximadamente una cuarta parte de la frecuencia máxima. Y esto continúa hasta que alcancemos el nivel máximo de descomposición.

El nivel máximo de descomposición se puede calcular utilizando la función pywt.wavedec (), mientras que la descomposición y los detalles se verán así:

Listado

 import pywt from pywt import wavedec from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data= sin (250 * pi * x**2) n_level=pywt.dwt_max_level(len(data), 'sym5') print('  : %s'%n_level) x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=7) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-7') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-7') grid() legend(loc='best') show()

Obtenemos:

Nivel máximo de descomposición: 7

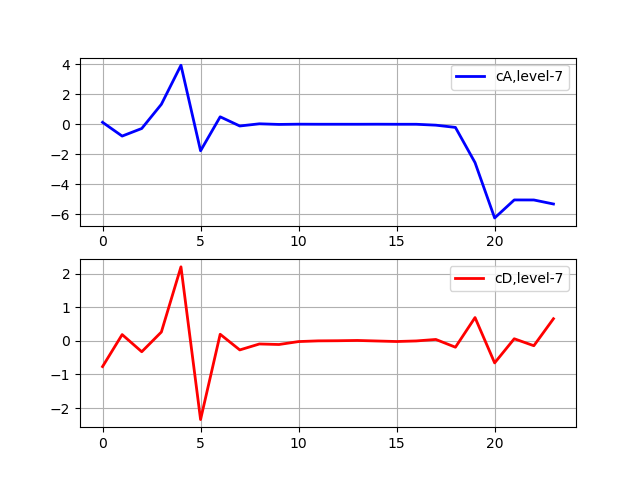
La descomposición se detiene cuando la señal se vuelve más corta que la longitud del filtro para una wavelet sym5 dada. Por ejemplo, supongamos que tenemos una señal con frecuencias de hasta 1000 Hz. En la primera etapa, separamos nuestra señal en partes de baja frecuencia y alta frecuencia, es decir, 0-500 Hz y 500-1000 Hz. En la segunda etapa, tomamos la parte de baja frecuencia y nuevamente la dividimos en dos partes: 0-250 Hz y 250-500 Hz. En la tercera etapa, dividimos la parte 0-250 Hz en la parte 0-125 Hz y la parte 125-250 Hz. Esto continúa hasta alcanzar el nivel máximo de descomposición.

Análisis de archivos wav usando fft Fourier y escalogramas wavelet

Para el análisis, use el archivo WebSDR . Considere el análisis de la señal reducida utilizando triang de scipy.signal y la implementación de la transformada discreta de Fourier en python (fft de scipy.fftpack). Si la longitud de la secuencia fft no es igual a 2n, en lugar de la transformada rápida de Fourier (fft), se realizará una transformada discreta de Fourier (dft). Así es como funciona este equipo.

Utilizamos el búfer de transformación rápida de Fourier de acuerdo con el siguiente esquema (datos numéricos, por ejemplo):

fftbuffer = np.zeros (15); crear un búfer lleno de ceros;
fftbuffer [: 8] = x [7:]; mover el final de la señal a la primera parte del búfer; fftbuffer [8:] = x [: 7]: movemos el comienzo de la señal a la última parte del búfer; X = fft (fftbuffer): consideramos la transformada de Fourier de un búfer lleno de valores de señal.

Para que el espectro de fases sea más legible, se aplica el despliegue de fases. Para hacer esto, cambie la línea con el cálculo de la característica de fase: pX = np.unwrap (np.angle (X)).

Listado para el análisis de fragmentos de señal fft

 import numpy as np from pylab import * from scipy import * import scipy.io.wavfile as wavfile M=501 hM1=int(np.floor((1+M)/2)) hM2=int(np.floor(M/2)) (fs,x)=wavfile.read('WebSDR.wav') x1=x[5000:5000+M]*np.hamming(M) N=511 fftbuffer=np.zeros([N]) fftbuffer[:hM1]=x1[hM2:] fftbuffer[N-hM2:]=x1[:hM2] X=fft(fftbuffer) mX=abs(X) pX=np.angle(X) suptitle(" WebSDR") subplot(3, 1, 1) st='  (WebSDR.wav)' plot(x,linewidth=2, label=st) legend(loc='center') subplot(3, 1, 2) st='    ' plot(mX,linewidth=2, label=st) legend(loc='best') subplot(3, 1, 3) st='    ' pX=np.unwrap(np.angle(X)) plot(pX,linewidth=2, label=st) legend(loc='best') show()

Para el análisis comparativo, utilizaremos un escalograma wavelet que se puede construir utilizando la función tree = pywt.wavedec (señal, 'coif5') en matplotlib.

Listado de escalogramas de wavelet

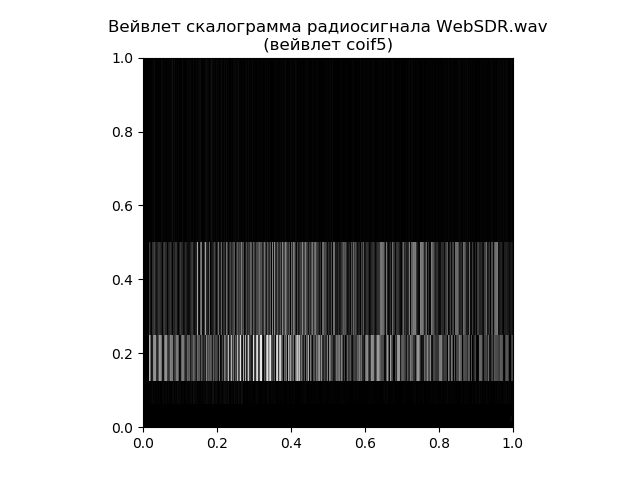
 from pylab import * import pywt import scipy.io.wavfile as wavfile #     ,     . def lepow2(x): return int(2 ** floor(log2(x))) #    MRA. def scalogram(data): bottom = 0 vmin = min(map(lambda x: min(abs(x)), data)) vmax = max(map(lambda x: max(abs(x)), data)) gca().set_autoscale_on(False) for row in range(0, len(data)): scale = 2.0 ** (row - len(data)) imshow( array([abs(data[row])]), interpolation = 'nearest', vmin = vmin, vmax = vmax, extent = [0, 1, bottom, bottom + scale]) bottom += scale #  ,   . rate, signal = wavfile.read('WebSDR.wav') signal = signal[0:lepow2(len(signal))] tree = pywt.wavedec(signal, 'coif5') gray() scalogram(tree) show()

Por lo tanto, el escalograma da una respuesta más detallada a la cuestión de la distribución de frecuencias a lo largo del tiempo, y la transformación rápida de Fourier es responsable de las frecuencias mismas. Todo depende de la tarea, incluso para un ejemplo tan simple.

Conclusiones

Se da la razón para usar una transformada wavelet discreta para señales dinámicas.
Se proporcionan ejemplos de análisis wavelet utilizando PyWavelets 1.0.3, un software gratuito de código abierto lanzado bajo la licencia MIT.
Se consideran herramientas de software para el uso práctico de la biblioteca PyWavelets.

Análisis Wavelet Parte 1

Introduccion

Cuándo usar la transformada wavelet en lugar de la transformada de Fourier

Las principales propiedades de las wavelets.

Modos de extensión de señal

Transformación discreta de wavelets

Banco de filtros

Análisis de archivos wav usando fft Fourier y escalogramas wavelet

Conclusiones

More articles: