Analizando un problema olímpico, recorreremos los sinuosos corredores de la generación de laberintos y su paso, y también veremos que en el lenguaje Julia la simplicidad de la implementación de algoritmos bordea su pseudocódigo.

Desafío

El laberinto es un cuadrado a cuadros de 10 por 10, en algunas celdas hay obstáculos, y en una celda hay una salida. El robot se encuentra en un laberinto y puede ejecutar 4 comandos: mover una celda hacia abajo, arriba, derecha o izquierda. Si el robot intenta ir más allá de los límites del laberinto o entrar en la jaula con un obstáculo, entonces permanece en su lugar. Si el robot entra por la salida, entonces sale del laberinto e ignora más comandos. Escriba un programa para el robot, ejecutando el cual el robot en cualquier caso llega a la salida, independientemente de la celda en la que se encontraba al principio. El programa debe consistir en no más de 1000 equipos.

Formato de entrada

No hay entrada Necesita escribir un programa para una condición específica especificada
El laberinto.
La versión del laberinto que puedes copiar. 0 - celda libre, 1 - obstáculo, x -
salida

0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000 

Formato de salida

Una línea que consta de caracteres U, D, R, L de longitud no más de 1000

Preparación

Los que no trabajaron con gráficos en Julia necesitan descargar paquetes

 using Pkg Pkg.add("Plots") Pkg.add("Colors") Pkg.add("Images") Pkg.build("Images") #     

Es más conveniente trabajar en Jupyter, ya que las imágenes se mostrarán directamente durante el trabajo. Aquí puede encontrar información sobre la instalación, así como una introducción y tareas para principiantes.

En la condición de nuestra tarea, hay una versión del laberinto para copiar

 S0 = "0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000" 

Para dibujar un laberinto, debes hacer una matriz. Como no queremos poner espacios manualmente, trabajaremos con la línea:

 S1 = prod(s-> s*' ', '['*S0*']') # prod(fun, arr)    arr #     fun #  julia  *   "[ 0 0 1 1 0 1 0 0 1 1 \n 0 1 0 0 0 0 1 0 0 0 \n 0 1 1 0 x 0 0 0 0 0 \n 0 0 1 0 0 0 0 1 0 0 \n 0 0 0 0 1 1 1 0 0 0 \n 0 0 0 0 1 0 0 1 0 0 \n 0 0 0 0 0 1 0 0 1 0 \n 0 1 0 0 1 0 1 0 1 0 \n 0 0 1 1 0 0 1 0 1 0 \n 1 0 0 0 0 1 1 0 0 0 ] " 

Reemplazando la incómoda letra x con un número y analizando la cadena, obtenemos una matriz entera que define nuestro laberinto. Luego, para mayor conveniencia, cambie los unos a ceros y los ceros a unos, y encierre el laberinto con una pared:

 S2 = replace(S1, 'x'=>'9') M0 = S2 |> Meta.parse |> eval m,n = size(M0) M1 = replace(M0, 1=>0, 0=>1) M = zeros(Int64,m+2,n+2) for i in 2:m+1, j in 2:n+1 M[i,j] = M1[i-1,j-1] end M # Maze map matrix 12×12 Array{Int64,2}: 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 

En la matriz

 length(M) 144 

células y de ellos

 sum(M)-9 70 

sobre el cual puedes caminar, es decir, posibles posiciones iniciales. Puede mostrar el resultado construyendo un histograma bidimensional

 using Plots heatmap(M, yaxis = :flip) # flip -   

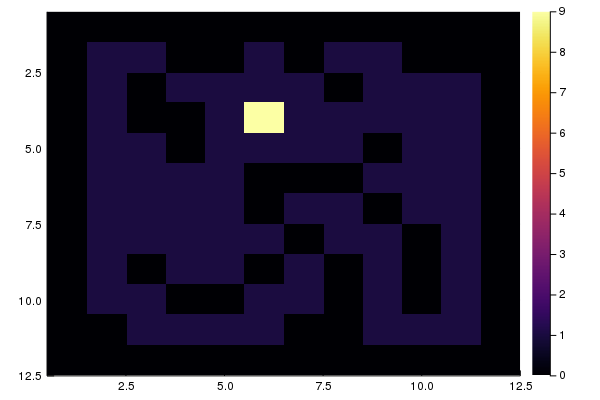
Verificación de la solución

En primer lugar, debe elaborar procedimientos que verifiquen la corrección de la solución propuesta. Establezca el tipo compuesto Point para usar la terminología de puntos y coordenadas:

 mutable struct Point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end 

Y ahora necesita aprender cómo traducir una secuencia de comandos que el robot pueda entender en código.

La idea es bastante simple: hay una coordenada inicial, aparece una línea con un algoritmo que indica cómo caminar. Tomamos una letra y miramos cuál de las celdas vecinas para pisar. A la coordenada actual agregamos el valor que está almacenado en esta celda. Es decir, si hay cero (muro), no nos hemos movido a ningún lado, de lo contrario, hemos dado un pequeño paso en la dirección requerida.

Usando el poder de la metaprogramación, puede reemplazar la secuencia de direcciones entrante con un código voluminoso y uniforme y ejecutarlo

 S = "RRLDUURULDDRDDRRRUUU" S1 = replace(S , "R"=>"c.y+=M[cx, c.y+1];") S1 = replace(S1, "L"=>"cy-=M[cx, cy-1];") S1 = replace(S1, "U"=>"c.x+=M[c.x+1, cy];") S1 = replace(S1, "D"=>"cx-=M[cx-1, cy];") #  - start point Sp = eval( Meta.parse(S1) ) 

Pero este método tiene una serie de inconvenientes, por lo tanto, utilizaremos los operadores condicionales clásicos. Por cierto, el hecho de que el número 9 indique la salida es un pequeño truco: para no verificar cada celda, y si es la salida, iniciamos el movimiento agregando el valor almacenado en una celda específica. Cuando el robot entra en la salida, se agrega un número deliberadamente grande a su coordenada, de modo que el robot vuela más allá de los límites de la matriz, lo que puede detectarse como un error al usar el bloque:

 try #     catch #       end 

Por lo tanto, implementamos una función que verificará si el robot llega a la salida a partir del punto c ejecución de comandos desde la cadena str :

 function isexit(str, c) scatter!([cy],[cx]) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end 

Recopilemos una función que iterará sobre todas las posiciones iniciales

 function test(Str) k = 0 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

Comprueba los comandos:

 S = "RRRLDUUURRRUUURRRRLLLRRUULDDDDRRRRDDDRRRUUU" heatmap(M, yaxis = :flip) test(S) # 10 test completed from 70 plot!(legend = false) 

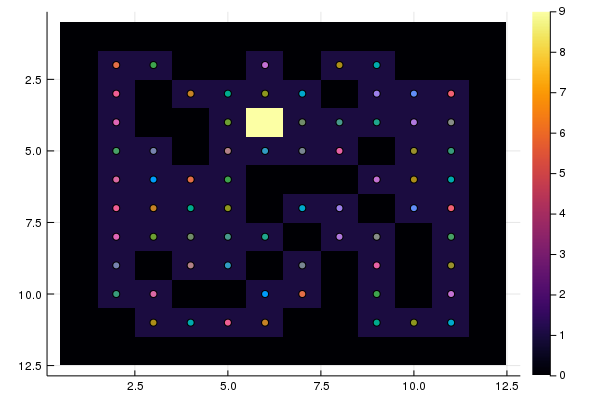
Todos los puntos de partida fueron probados, y solo 10 condujeron a la salida. Es necesario construir rutas desde cada punto hasta la salida.

Antes de sumergirnos en la generación y el paso de los laberintos, guardaremos nuestros resultados. Utilizaremos el paquete Images.jl que ofrece muchas posibilidades en el campo del procesamiento de imágenes (un buen ejemplo ). Una de sus herramientas de soporte es el paquete Colors.jl , que amplía la capacidad de Julia para trabajar con colores.

 using Images clrs(x) = x==9 ? RGB(1.,0.5,0) : RGB(x,x,x) maze = clrs.(M) # maze = Gray.(maze) # save("D:/dat/maze12x12.png", maze) 

Búsqueda de profundidad

Implementó la idea de un artículo sobre el Habr .
La idea es simple: crear una cuadrícula de muros

 M = 10 N = 10 A = [ i&j&1 for i in 0:N, j in 0:M ] # isodd(i) & isodd(j) & 1 Gray.(A) # from Images.jl 

luego, en bucle, atravesamos la ruta y las ramas. Definimos una función que encuentra áreas vecinas no visitadas (las designaremos, digamos, por un deuce) y devuelve uno de estos vecinos (si no hay vecinos no visitados, devuelve un punto de bandera):

 function neighbours2(A,p, n, m) nbrs = [Point(px, p.y+2), # up Point(px, py-2), # down Point(px-2, py), # left Point(p.x+2, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==2 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(-1,-1) end 

Romperemos las paredes así:

 function breakwall(A, newp,oldp) #  : x = (newp.x + oldp.x) >> 1 #   y = (newp.y + oldp.y) >> 1 A[x,y] = 1 end 

Algoritmo

1. Actualice la celda inicial y márquela como visitada.
2. Si bien hay celdas no visitadas
   1. Si la celda actual tiene "vecinos" no visitados
   1. Empuje la celda actual en la pila
   2. Seleccione una celda aleatoria de vecino
   3. Retire el muro entre la celda actual y la seleccionada
   4. Actualice la celda seleccionada y márquela como visitada.
   2. De lo contrario, si la pila no está vacía
   1. Saque la jaula de la pila
   2. Hazlo actual
   3. De lo contrario
   1. Seleccione una celda aleatoria no visitada, actualícela y márquela como visitada.

 function amazeng(n, m) M = [ 2(i&j&1) for i in 0:n, j in 0:m ]; p = Point(2,2) #   lifo = [] #   push!(lifo, p) #i = 0 while length(lifo) != 0 #     M[px,py] = 1 #     np = neighbours2(M, p, n, m) # new point #    -   if np.x == np.y == -1 p = pop!(lifo) else push!(lifo, p) breakwall(M, np, p) p = np #i+=1 #maze = Gray.(M/2) #save("D:/dat/maze$i.png", maze) end end M[1,2] = 1 #  M[n,m+1] = 1 #  Gray.(M) end 

 lbrnt = amazeng(36, 48) # save("D:/dat/maze111.png", lbrnt) 

Algoritmo de búsqueda de ruta de retroceso:

1. Actualice la celda inicial y márquela como visitada.
2. Hasta que se encuentre una solución
   1. Si la celda actual tiene "vecinos" no visitados
   1. Empuje la celda actual en la pila
   2. Seleccione una celda aleatoria de vecino
   3. Actualice la celda seleccionada y márquela como visitada.
   2. De lo contrario, si la pila no está vacía
   1. Saque la jaula de la pila
   2. Hazlo actual
   3. De lo contrario, no hay salida.

Estamos buscando vecinos por el contrario y dentro del radio de una celda, y no a través de una:

 function neighbours1(A, p, n, m) nbrs = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==1 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(0,0) end 

Defina un algoritmo para pasar el laberinto con el trazado de la ruta y los intentos fallidos

 function amazeng(img, start, exit) M = Float64.(channelview(img)) n, m = size(M) p = start M[exit.x,exit.y] = 1 lifo = [] push!(lifo, p) while px != exit.x || py != exit.y M[px,py] = 0.4 np = neighbours1(M, p, n, m) if np.x == np.y == 0 M[px,py] = 0.75 p = pop!(lifo) #  -  ,    #      else push!(lifo, p) p = np end end Gray.(M) end 

Como algunos han notado, también se llama una función, como la que generan los algoritmos (Programación múltiple). Cuando lo llame con dos números, resolverá el método de construcción del laberinto, pero si lo llama especificando la imagen y dos puntos (las coordenadas de entrada y salida) como argumento, entonces en la salida obtenemos una imagen con el laberinto pasado

 img0 = load("D:/dat/maze111.png") amazeng(img0) 

Probemos en nuestro laberinto:

 img0 = load("D:/dat/maze12x12.png") n, m = size(img0) amazeng(img0, Point(11,9), Point(4,6) ) 

Incluso si modifica la función para que se recuerde la ruta, el algoritmo sigue siendo ineficaz debido a los espacios abiertos. Pero los laberintos salen geniales.

Algoritmo aleatorizado de Prim

Tan pronto como comience a dibujar laberintos, no se detendrá. Realicemos otro algoritmo interesante:

• Comience con una cuadrícula llena de paredes.
• Seleccione una celda, márquela como parte del laberinto. Agregue paredes celulares a la lista de paredes.
• Si bien hay paredes en la lista:
  
  • Seleccione un muro aleatorio de la lista. Si solo se visita una de las dos celdas que comparte el muro, entonces:
    
    • Haz que la pared sea un pasaje y marca la celda no visitada como parte del laberinto.
    • Agregue paredes celulares adyacentes a la lista de paredes.
  • Eliminar el muro de la lista.

 neighbors(p::Point) = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right function newalls!(walls, p, maze, n, m) nbrs = neighbors(p) for a in nbrs if 1<ax<n-1 && 1<ay<m-1 && !maze[ax,ay] push!(walls, a) #       . end end end function breakwall!(p, maze, n, m) nbrs = neighbors(p) #       if sum( a-> maze[ax,ay], nbrs) == 1 for a in nbrs if maze[ax,ay] # true =  px == ax ? nx = px : px>ax ? nx = p.x+1 : nx = px-1 py == ay ? ny = py : py>ay ? ny = p.y+1 : ny = py-1 maze[px,py] = true #   maze[nx,ny] = true px = nx py = ny return true end end else return false end end function prim(n, m) M = falses(n,m); #    p = Point(2, 2) M[px,py] = true walls = [] newalls!(walls, p, M, n, m) while length(walls) != 0 p = splice!( walls, rand(1:length(walls)) ) if breakwall!(p, M, n, m) newalls!(walls, p, M, n, m) end end M end 

 primaze = prim(19,19); Gray.(primaze) 

Resulta más ramificado y no menos impresionante, especialmente el proceso de ensamblaje.

Y ahora implementamos el algoritmo más común para encontrar la ruta más corta:

Método A *

• Se crean 2 listas de vértices, pendientes y ya revisadas. Se agrega un punto de inicio a los pendientes, la lista de revisados ​​hasta ahora está vacía.
• Para cada punto se calcula $$$H$ - la distancia aproximada desde el punto al objetivo.
• De la lista de puntos a considerar, el punto con el menor $$$H$ . Dejala $$$X$ .
• Si $$$X$ - El objetivo, luego encontramos la ruta.
• Llevamos $$$X$ de la lista pendiente a la lista de ya revisados.
• Para cada uno de los puntos adyacentes a $$$X$ (denota este punto vecino $$$Y$ ), haga lo siguiente:
  
  • Si $$$Y$ ya en el revisado - sáltelo.
  • Si $$$Y$ aún no está en la lista de espera, agréguela allí.
• Si la lista de puntos a considerar está vacía, pero no hemos alcanzado la meta, entonces la ruta no existe.

Para comenzar, definamos el "punto" de clase que sabrá qué tan lejos está del objetivo:

 mutable struct Point_h x::Int64 # horisont y::Int64 # vertical h::Float64 Point_h(x, y) = new(x, y, 0.) end 

Ahora definimos una operación de comparación para la estructura, un método para establecer la presencia de un elemento en una matriz, así como la función de eliminar un elemento, encontrar la distancia entre puntos y enumerar vecinos:

 import Base: in, == ==(a::Point_h, b::Point_h) = ax==bx && ay==by function in(p::Point_h, Arr::Array{Point_h,1}) for a in Arr if a == p return true end end return false end function splicemin!(Arr)#::Array{Point_h,1} i = argmin( [ah for a in Arr] ) splice!(Arr, i) end dista(u,v) = hypot(vx-ux, vy-uy) # <=> sqrt( (vx-ux)^2 + (vy-uy)^2 ) neighbors(p::Point_h) = [Point_h(px, p.y+1), # up Point_h(px, py-1), # down Point_h(px-1, py), # left Point_h(p.x+1, py)] # right 

Como siempre, ¿se pueden aclarar operadores oscuros con el comando ? por ejemplo ?splice ?argmin .

Y, en realidad, el método A * en sí

 function astar(M, start, final) #   -       isgood(p) = 1<px<n && 1<py<m && M[px,py] != 0 n, m = size(M) #       start.h = dista(start,final) closed = [] opened = [] push!(opened, start) while length(opened) != 0 X = splicemin!(opened) if X in closed continue end if X == final break end push!(closed, X) nbrs = neighbors(X) ygrex = filter(isgood, nbrs) for Y in ygrex if Y in closed continue else Yh = dista(Y, final) push!(opened, Y) end end end #    closed # return end 

Cargamos la imagen con el laberinto y la presentamos en forma de matriz:

 img0 = load("D:/dat/maze0.png") mazematrix = Float64.(channelview(img0)) 

Y construimos una ruta para salir de un punto arbitrario:

 s = Point_h(11,9) # start f = Point_h(4,6) # finish M = copy(mazematrix) route = astar(M, s, f) i = 1 for c in route #   M[cx,cy] = 0.7 #save("D:/dat/Astar$i.png", M) i+=1 end Gray.(M) 

Una búsqueda desde todas las posiciones se ve así:

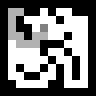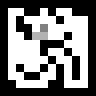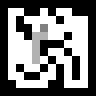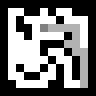
Visto que el agente corriendo siempre tiende al lado de la salida y a menudo se convierte en callejones sin salida, lo que da lugar a pasos innecesarios, y se recuerda toda la ruta. Esto se evita con una versión un poco más compleja del algoritmo A *.

• Se crean 2 listas de vértices, pendientes y ya revisadas. Se agrega un punto de inicio a los pendientes, la lista de revisados ​​hasta ahora está vacía.
• Para cada punto se calcula $$$F = G + H$ . $$$G$ - distancia desde el inicio hasta el punto, $$$H$ - la distancia aproximada desde el punto al objetivo. Cada punto también almacena un enlace al punto del que proviene.
• De la lista de puntos a considerar, el punto con el menor $$$F$ . Dejala $$$X$ .
• Si $$$X$ - El objetivo, luego encontramos la ruta.
• Llevamos $$$X$ de la lista pendiente a la lista de ya revisados.
• Para cada uno de los puntos adyacentes a $$$X$ (denota este punto vecino $$$Y$ ), haga lo siguiente:
  
  • Si $$$Y$ ya en el revisado - sáltelo.
  • Si $$$Y$ aún no está en la lista de espera: agréguela allí, recordando el enlace a $$$X$ y habiendo calculado $$$Y.G$ (esto es $$$X.G$ + distancia de $$$X$ antes $$$Y$ ) y $$$Y.H$ .
  • Si $$$Y$ en la lista para su consideración - verifique si $$$X.G$ + distancia de $$$X$ antes $$$Y$$$$<Y.G$ así que llegamos al punto $$$Y$ camino más corto, reemplazar $$$Y.G$ en $$$X.G$ + distancia de $$$X$ antes $$$Y$ y el punto desde el cual llegaron a $$$Y$ en $$$X$ .
• Si la lista de puntos a considerar está vacía, pero no hemos alcanzado la meta, entonces la ruta no existe.

Pero incluso con pasos innecesarios, nuestra opción está dentro de los límites de la tarea, por lo que modificar los programas será su tarea.

Hasta el final de la Olimpiada, no quedaba nada, pero aún necesitamos aprender a traducir los resultados de nuestros algoritmos en comandos de la forma "RRLUUDL..."

Y después de todos estos paseos por los laberintos, podemos suponer que la solución es mucho más simple. De hecho, una opción simple comienza de inmediato, pero realmente quería hacer cosas hermosas .

Si colocamos a nuestro artista en un área abierta e iniciamos caminatas aleatorias, dudará cerca de su posición inicial. Pero con la introducción de las paredes, algunas de las direcciones comenzarán a desvanecerse, los grados de libertad serán menores y, con los mismos datos de entrada, el agente se moverá una mayor distancia.

Aquí está nuestra versión de verificar la idoneidad de los equipos para rescatar un robot de un laberinto:

 M = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0] mutable struct Point # point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end function isexit(str, c) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end function test(Str) k = 0 n, m = 10,10 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

Ahora es suficiente generar líneas aleatorias hasta que obtenga una que funcione para todas las posiciones iniciales:

 using Random S = randstring("RLUD",200) "RDRRRDLRLUULURUDUUDLLLLLULLUDRRURDLDLULLRLUUUDURUUUULRUDUURUUDLRLLULRLUDRRLRRULLDULRRRRULRLLDULRLDRUDURDRUUDUUDDDDDLURRRRDRDURRRDDLLDUURRRLDRUDLRLLRDDRLRRRDDLLLRUURDRLURDLLUULLLLUURLLULUDULDDLDLLRLDUD" test(S) 41 test completed from 70 

Además, era posible no preocuparse por la prueba. Fue suficiente para leer la tarea y generar una cadena aleatoria con la condición máxima permitida:

 for i in 1:20 S = randstring("RLUD",1000) test(S) end 70 test completed from 70 70 test completed from 70 70 test completed from 70 70 test completed from 70 55 test completed from 70# 65 test completed from 70# 70 test completed from 70 70 test completed from 70 38 test completed from 70# 70 test completed from 70 70 test completed from 70 56 test completed from 70# 70 test completed from 70 70 test completed from 70 70 test completed from 70 16 test completed from 70# 70 test completed from 70 24 test completed from 70# 70 test completed from 70 70 test completed from 70 

Es decir, con una probabilidad del 70%, la línea pasaría las pruebas.

Eso es todo Le deseo al lector una aleatoriedad exitosa, paciencia e intuición para obtener soluciones obvias.

Para los curiosos: enlaces para profundizar en el tema:

• La excursión más completa a la generación del laberinto.
• Versión rusa
• Métodos de tiempos
• Dos métodos
• Algoritmo de Eller
• Generador en línea
• Métodos para encontrar el camino entre puntos en línea
• Algoritmo de ruta de búsqueda de punto de salto
• A * en Wikipedia
• Introducción a A *
• Introducción al algoritmo A *
• Explicación de los algoritmos de búsqueda de ruta
• Fuente de arte