Este comentario fue impulsado por la redacción del artículo. Más precisamente, una frase de ella.

... gastar memoria o ciclos de procesador en artículos en miles de millones de dólares no es bueno ...

Sucedió que recientemente tuve que hacer precisamente eso. Y, aunque, el caso que consideraré en el artículo es bastante especial: las conclusiones y las soluciones aplicadas pueden ser útiles para alguien.

Un poco de contexto

La aplicación iFunny se ocupa de una gran cantidad de contenido gráfico y de video, y la búsqueda difusa de duplicados es una de las tareas más importantes. Esto en sí mismo es un gran tema que merece un artículo separado, pero hoy solo hablaré un poco sobre algunos enfoques para calcular matrices muy grandes de números en relación con esta búsqueda. Por supuesto, todos tienen una comprensión diferente de las "matrices muy grandes", y sería una tontería competir con el Colisionador de Hadrones, pero aún así. :)

Si el algoritmo es muy breve, entonces para cada imagen se crea su firma digital (firma) a partir de 968 enteros, y la comparación se realiza al encontrar la "distancia" entre las dos firmas. Teniendo en cuenta que el volumen de contenido solo en los últimos dos meses ascendió a unos 10 millones de imágenes, entonces un lector atento lo descubrirá fácilmente en su mente: estos son exactamente los "elementos en miles de millones de volúmenes". A quién le importa, bienvenido a cat.

Al principio habrá una historia aburrida sobre el ahorro de tiempo y memoria, y al final habrá una breve historia instructiva sobre el hecho de que a veces es muy útil mirar la fuente. Una imagen para llamar la atención está directamente relacionada con esta historia instructiva.

Debo admitir que era un poco astuto. En un análisis preliminar del algoritmo, fue posible reducir el número de valores en cada firma de 968 a 420. Ya es el doble de bueno, pero el orden de magnitud sigue siendo el mismo.

Aunque, si lo piensas bien, no es tanto lo que estaba engañando, y esta será la primera conclusión: antes de continuar con la tarea, vale la pena pensar: ¿es posible de alguna manera simplificarla de antemano?

El algoritmo de comparación es bastante simple: se calcula la raíz de la suma de los cuadrados de las diferencias de las dos firmas, se divide por la suma de los valores calculados previamente (es decir, en cada iteración la suma seguirá siendo y no puede deducirse como una constante) y se comparará con el valor umbral. Vale la pena señalar que los elementos de firma están limitados a valores de -2 a +2 y, en consecuencia, el valor absoluto de la diferencia está limitado a valores de 0 a 4.


Nada complicado, pero la cantidad decide.

Primer acercamiento ingenuo

//  const val d = 0.3 // 10.000.000 . //      , //        val collection: MutableList<Signature> = mutableListOf() // signature —   420   Byte class Signature(val signature: Array<Byte>, val norma: Double) fun getSimilar(signature: Signature) = collection .filter { calculateDistance(it, signature) < d } fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> Math.pow((value - second.signature[index]).toDouble(), 2.0) }.sum()) / (first.norma + second.norma) 

Calculemos lo que tenemos aquí con el número de operaciones:

10M Square Roots Math.sqrt
10M adiciones y divisiones / (first.norma + second.norma)
4.200M sustracciones y cuadratura Math.pow((value - second.signature[index]).toDouble(), 2.0)
4.200M adiciones .sum()

¿Qué opciones tenemos?

1. Con tales volúmenes, gastar un Byte completo (o, Dios no lo quiera, alguien habría adivinado usar Int ) para almacenar tres bits significativos es un desperdicio imperdonable.
2. Quizás, ¿cómo reducir la cantidad de matemáticas?
3. Pero, ¿es posible hacer un filtrado preliminar, que no es tan costoso desde el punto de vista computacional?

El segundo enfoque, empacamos

Por cierto, si alguien sugiere cómo puede simplificar los cálculos con dicho paquete, recibirá un gran agradecimiento y más en karma. Aunque uno, pero con todo mi corazón :)

One Long es de 64 bits, lo que, en nuestro caso, nos permitirá almacenar 21 valores (y 1 bit permanecerá sin resolver).

 //   20   Long class Signature(val signature: Array<Long>, val norma: Double) fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> calculatePartial(value, second.signature[index]) }.sum()) / (first.norma + second.norma) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L (0..60 step 3).onEach { val current = (first.ushr(it) and 0x7) - (second.ushr(it) and 0x7) sum += current * current } return sum.toDouble() } 

Es mejor desde la memoria ( 4.200M versus 1.600M bytes, si es más o menos), pero ¿qué pasa con los cálculos?

Creo que es obvio que el número de operaciones se ha mantenido igual y se 8.400M agregado 8.400M turnos y 8.400M lógicos. Quizás se pueda optimizar, pero la tendencia aún no es feliz, esto no es lo que queríamos.

El tercer enfoque, volver a empacar con subsub

Por la mañana puedo olerlo, ¡aquí puedes usar un poco de magia!

Guardemos los valores no en tres, sino en cuatro bits. De esta manera:

Sí, perderemos densidad de empaque en comparación con la versión anterior, pero por otro lado, podremos recibir Long con 16 (no del todo) diferencias con un XOR 'ohm a la vez. Además, solo habrá 11 opciones para la distribución de bits en cada mordisco final, lo que le permitirá utilizar valores precalculados de los cuadrados de las diferencias.

 //   27   Long class Signature(val signature: Array<Long>, val norma: Double) // -1    val precomputed = arrayOf(0, 1, 1, 4, 1, -1, 4, 9, 1, -1, -1, -1, 4, -1, 9, 16) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L val difference = first xor second (0..60 step 4).onEach { sum += precomputed[(difference.ushr(it) and 0xF).toInt()] } return sum.toDouble() } 

De memoria se convirtió en 2.160M frente a 1.600M , desagradable, pero aún mejor que el 4.200M inicial.

Calculemos las operaciones:

10M raíces cuadradas, adiciones y divisiones (no se han ido a ninguna parte)
270M XOR
4.320 adiciones, cambios, 4.320 lógicos y extractos de la matriz.

Ya parece más interesante, pero, de todos modos, hay demasiados cálculos. Desafortunadamente, parece que ya hemos gastado ese 20% de los esfuerzos dando el 80% del resultado y es hora de pensar en dónde más puede beneficiarse. Lo primero que viene a la mente es no llevarlo a un cálculo, filtrando firmas obviamente inapropiadas con algún filtro liviano.

Cuarto enfoque, tamiz grande

Si transforma ligeramente la fórmula de cálculo, puede obtener esta desigualdad (cuanto menor sea la distancia calculada, mejor):


Es decir ahora necesitamos descubrir cómo calcular el valor mínimo posible del lado izquierdo de la desigualdad en función de la información que tenemos sobre el número de bits establecidos en Long 's. Luego simplemente descarte todas las firmas que no lo satisfagan.
Permítame recordarle que x puedo tomar valores de 0 a 4 (el signo no es importante, creo que está claro por qué). Dado que cada término es cuadrado, es fácil derivar un patrón general:


La fórmula final se ve así (no la necesitaremos, pero la deduje durante mucho tiempo y sería una pena olvidar y no mostrar a nadie):


Donde B es el número de bits establecido.

De hecho, en un solo Long 64 bits, lea 64 resultados posibles. Y se calculan de antemano perfectamente y se agregan a una matriz, por analogía con la sección anterior.

Además, es completamente opcional calcular los 27 Longs: es suficiente para superar el umbral en el siguiente y puede interrumpir el cheque y devolver falso. El mismo enfoque, por cierto, se puede utilizar en el cálculo principal.

 fun getSimilar(signature: Signature) = collection .asSequence() //     !? .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } val estimateValues = arrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 69, 74, 79, 84, 89, 94, 99, 104, 109, 114, 119, 124, 129, 134, 139, 144, 151, 158, 165, 172, 179, 186, 193, 200, 207, 214, 221, 228, 235, 242, 249, 256) fun estimate(first: Signature, second: Signature):Boolean{ var bitThreshold = Math.pow(d * (first.norma + second.norma), 2.0).toLong() first.signature.forEachIndexed { index, value -> bitThreshold -= estimateValues[java.lang.Long.bitCount(value xor second.signature[index])] if (bitThreshold <= 0) return false } return true } 

Aquí debe entenderse que la efectividad de este filtro (hasta negativo) depende desastrosamente del umbral seleccionado y, un poco menos fuerte, de los datos de entrada. Afortunadamente, para el umbral requerido d=0.3 un número bastante pequeño de objetos logra pasar el filtro y la contribución de su cálculo al tiempo de respuesta total es tan escasa que puede descuidarse. Y si es así, puede ahorrar un poco más.

Quinto enfoque, deshacerse de la secuencia

Cuando se trabaja con grandes colecciones, la sequence es una buena defensa contra la memoria extremadamente desagradable. Sin embargo, si obviamente sabemos que en el primer filtro la colección se reducirá a un tamaño razonable, entonces una opción mucho más razonable sería usar la iteración ordinaria en un bucle con la creación de una colección intermedia, porque la sequence no solo es moderna y juvenil, sino también un iterador, que hasNext compañeros que están lejos de ser gratis.

 fun getSimilar(signature: Signature) = collection .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } 

Parecería que aquí está la felicidad, pero quería "hacerlo hermoso". Aquí llegamos a la historia instructiva prometida.

Sexto enfoque, queríamos lo mejor

Escribimos en Kotlin, y aquí algunos extranjeros java.lang.Long.bitCount ! Y más recientemente, los tipos sin firmar se introdujeron en el idioma. Ataque

Apenas dicho que hecho. Todos los ULong reemplazan por ULong , ULong de la fuente Java y se reescribe como una función de extensión para ULong

 fun ULong.bitCount(): Int { var i = this i = i - (i.shr(1) and 0x5555555555555555uL) i = (i and 0x3333333333333333uL) + (i.shr(2) and 0x3333333333333333uL) i = i + i.shr(4) and 0x0f0f0f0f0f0f0f0fuL i = i + i.shr(8) i = i + i.shr(16) i = i + i.shr(32) return i.toInt() and 0x7f } 

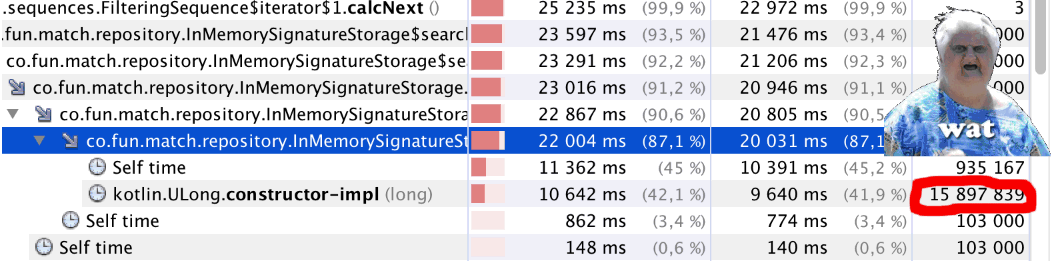
Comenzamos y ... Algo está mal. El código comenzó a funcionar notablemente más lento. Iniciamos el generador de perfiles y vemos algo extraño (ver el bitCount() artículo): un poco menos de un millón de llamadas a bitCount() casi 16 millones de llamadas a Kotlin.ULong.constructor-impl . WAT?

El enigma se explica simplemente: solo mira el código de clase ULong

 public inline class ULong @PublishedApi internal constructor(@PublishedApi internal val data: Long) : Comparable<ULong> { @kotlin.internal.InlineOnly public inline operator fun plus(other: ULong): ULong = ULong(this.data.plus(other.data)) @kotlin.internal.InlineOnly public inline operator fun minus(other: ULong): ULong = ULong(this.data.minus(other.data)) @kotlin.internal.InlineOnly public inline infix fun shl(bitCount: Int): ULong = ULong(data shl bitCount) @kotlin.internal.InlineOnly public inline operator fun inc(): ULong = ULong(data.inc())  .. } 

No, entiendo todo, ULong es experimental ahora, pero ¿cómo es eso?
En general, reconocemos el enfoque como fallido, lo cual es una pena.

Bueno, pero aún así, ¿quizás algo más se pueda mejorar?

En realidad puedes. El código original java.lang.Long.bitCount no es el más óptimo. Da un buen resultado en el caso general, pero si sabemos de antemano en qué procesadores funcionará nuestra aplicación, entonces podemos elegir una forma más óptima: aquí hay un muy buen artículo al respecto en Habré. Recomiendo mucho contar los bits individuales , recomiendo leerlo.

Usé el "Método combinado"

 fun Long.bitCount(): Int { var n = this n -= (n.shr(1)) and 0x5555555555555555L n = ((n.shr(2)) and 0x3333333333333333L) + (n and 0x3333333333333333L) n = ((((n.shr(4)) + n) and 0x0F0F0F0F0F0F0F0FL) * 0x0101010101010101).shr(56) return n.toInt() and 0x7F } 

Contando loros

Todas las mediciones se hicieron al azar, durante el desarrollo en la máquina local y se reproducen de la memoria, por lo que es difícil hablar de precisión, pero puede estimar la contribución aproximada de cada enfoque.

Conclusiones

• Cuando se trata del procesamiento de grandes cantidades de datos, vale la pena dedicar tiempo a un análisis preliminar. Quizás no todos estos datos necesitan ser procesados.
• Si puede utilizar un filtrado previo grueso, pero barato, esto puede ayudar mucho.
• Un poco de magia es nuestro todo. Bueno, donde corresponda, por supuesto.
• Observar los códigos fuente de las clases y funciones estándar a veces es muy útil.

Gracias por su atencion! :)

Y sí, para continuar.