Para transmitir un mensaje desde una estación base a un dispositivo móvil (y viceversa), una onda electromagnética tiene que superar una cantidad significativa de obstáculos: reflexión, refracción, dispersión, sombreado, cambios de frecuencia Doppler, etc. Primero, todos estos efectos se llaman multiplicativos (del inglés. Multiplicación - multiplicación) - de acuerdo con el modelo matemático de tales efectos. Y, en segundo lugar, se puede recoger bajo el término general de desvanecimiento .
De estándar en estándar, de generación en generación, de tecnología en tecnología, los científicos e ingenieros han luchado y están luchando con el problema de nivelar estos desvanecimientos (mitigación de desvanecimiento).
Y algunas soluciones están muy extendidas. Digamos más: casi todos, de una forma u otra, están asociados con el concepto de diversidad .
La fuente de la ilustración (no, esto no es publicidad, solo una combinación exitosa del término deseado y el gato).
Un ejemplo de tales soluciones:
- Salto de frecuencia - contra desvanecimiento selectivo de frecuencia;
- Estimación y ecualización de canales a través de retroalimentación - GSM, para suprimir cambios en el dominio del tiempo;
- Extensión de espectro (UMTS);
- Señales piloto (comenzando con UMTS) en el enlace descendente (enlace descendente) y seguimiento de señal (seguimiento de señal) en el enlace ascendente (enlace ascendente) - para suprimir los cambios en el dominio del tiempo;
- OFDM - LTE, contra el desvanecimiento selectivo de frecuencia;
- Diversidad temporal ( codificación de corrección de errores );
- Diversidad de polarización (en el lado del transmisor) + Adders (combinadores, en el lado del receptor);
- Diversidad espacial .
La última de estas técnicas la consideraremos hoy como parte de otro tema sobre MIMO .
Orden de diversidad espacial y ganancia de matriz
El primero
Existe ese concepto: el orden de diversidad espacial: si la misma información se puede recopilar desde diferentes direcciones , entonces la esperanza de restaurarla aumentará correctamente. Como ejemplo de la vida, podemos imaginar la recopilación de información sobre el mismo evento de fuentes de informantes independientes. En las comunicaciones por radio, podemos aumentar este orden, incluso mediante el uso de MISO , SIMO o MIMO .
El límite teórico de tal diversidad. 
donde 
- el número de antenas de transmisión, y 
- el número de antenas receptoras. Recuerda esto
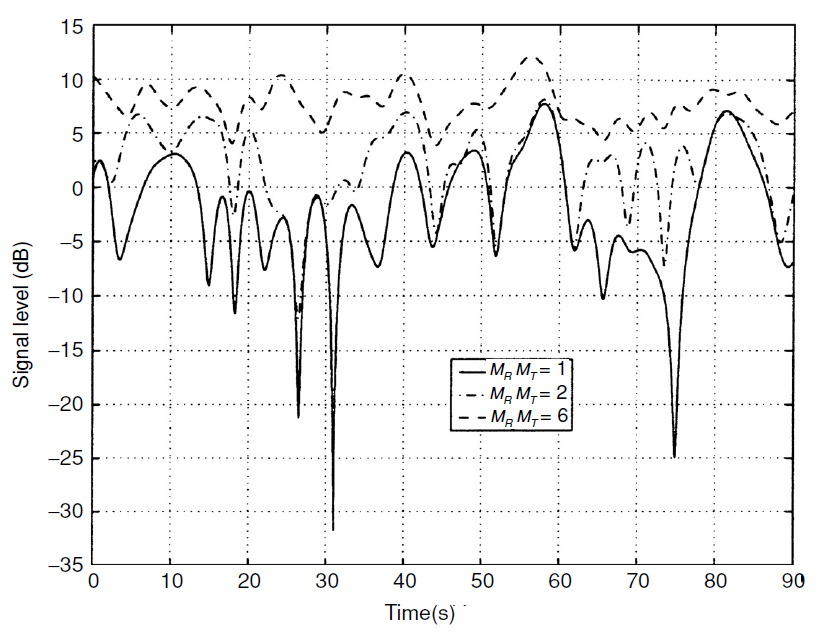
Fig.1. Estabilidad del canal causada por un aumento en el orden de diversidad espacial. En valores 
el canal está completamente estabilizado y se convertirá en un canal sin desvanecimiento (AWGN) [1, p . 101] .
El segundo
Usando SIMO , MIMO e incluso MISO (en el caso de un canal conocido), se puede obtener la llamada ganancia de matriz . Esto significa que el uso de múltiples antenas de recepción y / o la distribución adecuada de energía en el lado de transmisión puede aumentar la relación señal-ruido (SNR) y, por lo tanto, reducir el número de errores.
Los órdenes de diversidad y ganancia de matriz para diversas configuraciones pueden derivarse analíticamente [1, p. 86 - 100] y reducir a una tabla [1, p. 101] tanto para el caso cuando se desconoce el canal (CU - Canal desconocido) como para el caso cuando se conoce el canal (CK - Canal desconocido) en el lado del transmisor.
De acuerdo, incluso con trazos amplios, pero ahora tenemos al menos cierta comprensión de los aspectos teóricos de la supresión del desvanecimiento. La siguiente pregunta es ¿cómo alcanzar estos límites teóricos? ¿Cuáles son las técnicas para activar las ganancias consideradas?
Solución No. 1. Códigos de espacio-tiempo
Una de las clases más populares de soluciones para la diversidad espacial es, quizás, la clase de códigos espacio-temporales (códigos espacio-temporales). Por ejemplo, creo que muchos métodos familiares de Alamouti (un ejemplo de código de bloque) [2, p. 40-46]:
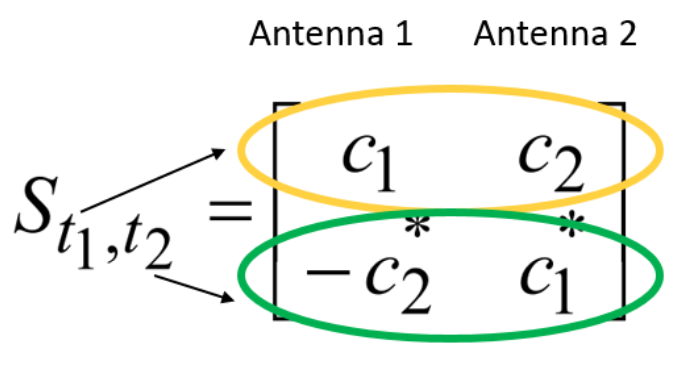
donde 
a las 
Son algunos caracteres de entrada 
a las Son franjas horarias, y 
- esto es, de hecho, una matriz de codificación.
El esquema de Alamouti es ortogonal [1, pp. 93-95, 97-98] y, lo más importante, no requiere información del estado del canal.
La descripción matemática de la transmisión de la señal codificada por el esquema Alamouti, así como varios ejemplos de modelado de esta técnica en MatLab se pueden encontrar en mi repositorio . Interesado en bienvenido!
Sin embargo, como puede ver, el circuito de Alamouti es un caso en el que solo tenemos dos antenas de transmisión ( 
)
Pero no se desanime con anticipación: por supuesto, hay otras opciones disponibles, simplemente se les llama un poco diferentes. Por ejemplo, según [3], se pueden aplicar los siguientes esquemas de codificación:
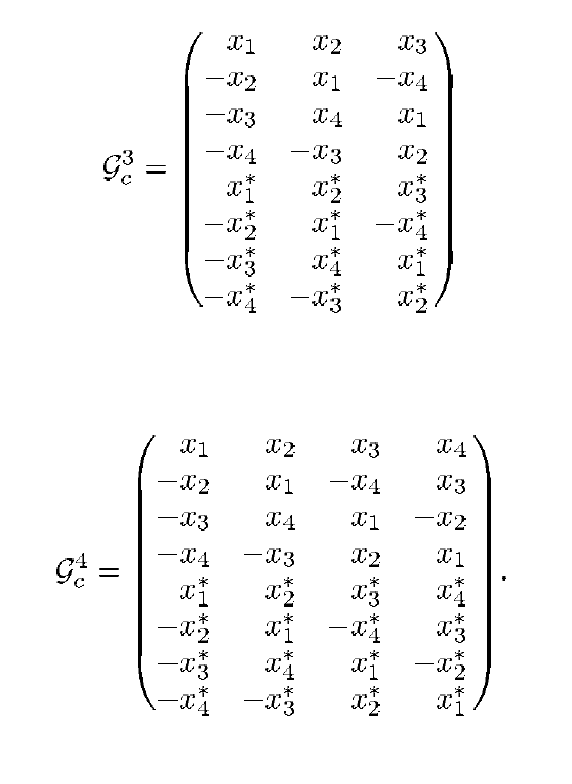
Fig. 2. Esquemas de transferencia para casos 
y 
[2]
Y hay muchas otras opciones: solo para cumplir con las condiciones de ortogonalidad.
Dichos códigos requieren, de hecho, los mismos procedimientos para codificar y decodificar que para el código Alamouti. Por lo tanto, generalmente se combinan bajo el término general códigos de bloque de espacio-tiempo ortogonales (OSTBC - Códigos de bloque de espacio-tiempo ortogonales ).
Se presta mucha atención a esta clase de códigos en los materiales "Introducción a los sistemas MIMO" de MathWorks. ¡Recomiendo encarecidamente a todos los interesados que lo lean!
Cual es el precio
Como se puede ver en el esquema de transmisión, aunque transmitimos símbolos en paralelo, pasamos varios intervalos de tiempo en esto. Por lo tanto, sacrificamos el ancho de banda (al menos, lo obtenemos menos). Para el esquema de Alamouti, este compromiso es simétrico: utilizamos 2 antenas y 2 ranuras de tiempo (como si usara SISO en términos de ancho de banda). Otros esquemas pueden afectar la velocidad de transmisión aún más.
Decisión número 2. DET: transmisión de modo propio dominante
Bueno, para la clase de técnicas anterior, el conocimiento del canal no era importante para nosotros. Pero, ¿y si todavía tenemos este conocimiento? ¿Hay alguna técnica más adecuada en este caso?
En uno de mis artículos anteriores, discutimos que, teniendo conocimiento del estado del canal disponible, podemos aplicar varios métodos de procesamiento de señal para aumentar el rendimiento. El mismo principio funciona para aumentar la inmunidad al ruido.
Probablemente, muchos han escuchado sobre el método MRC y muchos saben que este método es muy adecuado para el caso SIMO , cuando hay al menos una antena en la transmisión, pero todavía hay muchas, lo que significa que hay algo para combinar.
Pero, probablemente, ya un número menor de lectores encontró MRC en el lado de transmisión (Tx-MRC) [1, p. 95.96], y aún menos con la tecnología DET (transmisión de modo propio dominante) [1, p. 98-100]. Arreglarlo!
Para comenzar, considere el caso general del canal MIMO y el último de estos métodos: DET.
¿Cuál es la esencia de:
- Si el transmisor tiene una matriz
entonces puede ser procesado. - Por ejemplo, descomponerlo a través de SVD :
obteniendo así varias matrices de una determinada propiedad. - Estas propiedades se pueden utilizar para optimizar la transferencia, por ejemplo, utilizando la codificación previa (codificación previa).
Introducimos algunos vectores de precodificación:
donde 
Es el primer vector matriz (dominante, por así decirlo) 
.
Además, también podemos escribir el vector de procesamiento posterior:
donde 
Es el primer vector de la matriz. 
.
Redefina el modelo de la señal recibida (vea el tema del ancho de banda ):
Voila! La magia del álgebra lineal destacó entre todas las rutas de distribución la más rentable y dirigió toda la energía allí. De hecho, tenemos ante nosotros un algoritmo lineal de formación de haces.
A costa de este enfoque, al igual que en el caso de OSTBC, la limitación de ancho de banda es. Es cierto que esto está sucediendo únicamente en el dominio espacial.
¿Por qué el método contiene valores propios en su nombre si solo estuviéramos hablando de valores singulares?Debido a que los valores propios (cardinalidad de las rutas de propagación - desvanecimiento) pueden derivarse directamente de números singulares (amplitudes de desvanecimiento):
Bueno, con DET está más o menos claro ¿qué pasa con Tx-MRC?
Es aún más fácil con él: este es un caso especial de DET, y ahora lo demostraremos.
Para Tx-MRC, se propone el siguiente vector de precodificación en la literatura:
Tenemos en cuenta que el cuadrado de la norma de Frobenius es igual al valor propio y, en consecuencia, el cuadrado del número singular 
(en el caso de SIMO y MISO).
Por otra parte, redefinimos el modelo de la señal recibida, solo para el caso MISO:
Lo cual se requería para probar.
Tenga en cuenta que ahora estamos hablando no solo de la separación de señales en el lado transmisor y de combinarlas en el lado receptor, como fue el caso con OSTBC. Ahora estamos hablando de la distribución óptima de energía. Esto significa que los valores de ganancia de matriz en este caso son más altos que los de OSTBC.
Ahora que se han pronunciado todas las palabras, intentaremos simular nuestras técnicas.
Modelado
Hoy conté un poco: para el modelado OSTBC , se usaron objetos listos para usar de Communication Toolbox (MatLab R2014a, cuál era):
Para la modulación y demodulación (y cálculo de error de bit - BER), las funciones ya no se utilizaron, sino las funciones . Sus análogos están en el paquete Octave de comunicaciones .
Los códigos fuente se pueden encontrar aquí.clear all; close all; clc snapshots = 100000; EbNo = 0:15; M = 2;
Debería resultar algo como esto:
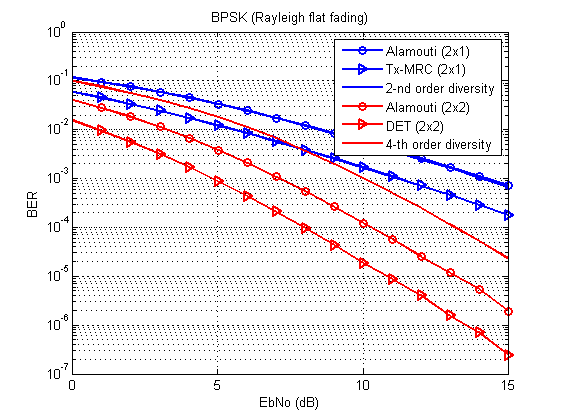
Fig. 3. Curvas de error de bit / símbolo para diferentes técnicas de transmisión (BPSK, canal Rayleigh con desvanecimiento plano). Comparar con [1, p. 96, 100].
Y ahora la pregunta es: ¿dónde está la curva del límite teórico de la diversidad de segundo orden?
La respuestaTodo está de acuerdo con la tabla: esta curva coincide completamente con el Alamouti 2x1. En el caso de MIMO, la ganancia de matriz también entra en juego, por lo que las curvas se separan.
De una forma u otra, y se espera que el DET (o Tx-MRC) supere al Alamouti en calidad.
Así: ¡el conocimiento es poder!
Literatura
Paulraj, Arogyaswami, Rohit Nabar y Dhananjay Gore. Introducción a las comunicaciones inalámbricas espacio-temporales. Cambridge University Press, 2003.
Bakulin M. G., Varukina L. A., Kreindelin V. B. Tecnología MIMO: principios y algoritmos // M.: Línea directa - Telecom. - 2014 .-- T. 244.
Tarokh, V., Jafarkhani, H. y Calderbank, AR (1999). Códigos de bloques espacio-temporales de diseños ortogonales. IEEE Transactions on Information teoría, 45 (5), 1456-1467.
PS
¡Al personal docente y a la fraternidad estudiantil de mi profesión nativa les saludo!