Introducción al aprendizaje automático

El curso completo en ruso se puede encontrar en este enlace .
El curso de inglés original está disponible en este enlace .



Nuevas conferencias están programadas cada 2-3 días.

Entrevista con Sebastian Trun, CEO de Udacity

"Hola de nuevo, soy Paige y tú eres mi invitado hoy, Sebastián".
- Hola, soy Sebastian!
- ... un hombre que tiene una carrera increíble, ¡que logró hacer muchas cosas increíbles! Usted es cofundador de Udacity, fundó Google X, es profesor en Stanford. Has estado haciendo una investigación increíble y un aprendizaje profundo a lo largo de tu carrera. ¿Qué le trajo la mayor satisfacción y en cuáles de las áreas recibió más recompensas por el trabajo realizado?
- Francamente, ¡me encanta estar en Silicon Valley! Me gusta estar al lado de personas que son mucho más inteligentes que yo, y siempre he considerado la tecnología como una herramienta que cambia las reglas del juego de varias maneras, desde educación hasta logística, atención médica, etc. Todo esto cambia muy rápido, y existe un deseo increíble de participar en estos cambios, de observarlos. Miras a tu alrededor y entiendes que la mayoría de lo que ves a tu alrededor no funciona como debería, ¡siempre puedes inventar algo nuevo!
- Bueno, esta es una visión muy optimista de la tecnología. ¿Cuál fue el mayor eureka a lo largo de tu carrera?
- ¡Señor, había tantos! Recuerdo uno de los días en que Larry Page me llamó y me sugirió crear autos piloto automático que pudieran conducir por todas las calles de California. En ese momento me consideraban un experto, me clasificaban entre ellos y era la misma persona que decía "no, esto no se puede hacer". Después de eso, Larry me convenció de que, en principio, es posible hacer esto, solo tienes que comenzar y probar. Y lo hicimos! Este fue el momento en que me di cuenta de que incluso los expertos están equivocados y diciendo "no" somos 100% pesimistas. Creo que deberíamos estar más abiertos a lo nuevo.
"O, por ejemplo, si Larry Page te llama y te dice:" Oye, haz algo genial como Google X ", ¡y obtienes algo genial!
- Sí, eso es seguro, no hay necesidad de quejarse! Quiero decir, todo esto es un proceso que pasa por muchas discusiones sobre el camino a la implementación. Tengo mucha suerte de trabajar y estoy orgulloso de ello, en Google X y en otros proyectos.
- Impresionante! Entonces, este curso se trata de trabajar con TensorFlow. ¿Tiene experiencia en el uso de TensorFlow o tal vez está familiarizado (escuchado) con él?
- si! ¡Literalmente amo TensorFlow, por supuesto! En mi propio laboratorio, lo usamos a menudo y mucho, uno de los trabajos más importantes basado en TensorFlow se lanzó hace unos dos años. Aprendimos que iPhone y Android pueden ser más efectivos para detectar el cáncer de piel que los mejores dermatólogos del mundo. Publicamos nuestra investigación en Nature y esto creó una especie de conmoción en la medicina.
- Eso suena increíble! ¡Así que conoces y amas TensorFlow, que es genial en sí mismo! ¿Ya has trabajado con TensorFlow 2.0?
- No, lamentablemente aún no he tenido tiempo.
- ¡Será simplemente increíble! Todos los estudiantes en este curso trabajarán con esta versión.
- Los envidio! ¡Definitivamente lo intentaré!
- Genial! En nuestro curso hay muchos estudiantes que en su vida nunca se han dedicado al aprendizaje automático, por la palabra "completamente". Para ellos, el campo puede ser nuevo, quizás para alguien que la programación en sí sea nueva. ¿Qué consejo tienes para ellos?
- Me gustaría que permanecieran abiertos - a nuevas ideas, técnicas, soluciones, posiciones. El aprendizaje automático es en realidad más fácil que la programación. En el proceso de programación, debe tener en cuenta cada caso en los datos de origen, adaptar la lógica del programa y las reglas para ello. En este mismo momento, usando TensorFlow y el aprendizaje automático, esencialmente entrena a la computadora usando ejemplos, permitiendo que la computadora encuentre las reglas por sí misma.
- ¡Esto es increíblemente interesante! ¡No puedo esperar para contarles a los estudiantes en este curso un poco más sobre el aprendizaje automático! Sebastian, ¡gracias por tomarte el tiempo de venir hoy!
- gracias! Mantente en contacto!

¿Qué es el aprendizaje automático?

Entonces, comencemos con la siguiente tarea: valores de entrada y salida dados.



Cuando tiene el valor 0 como valor de entrada, luego 32 como valor de salida Cuando tiene 8 como valor de entrada, luego 46.4 como valor de salida. Cuando tiene 15 como valor de entrada, luego 59 como valor de salida, y así sucesivamente.

Eche un vistazo más de cerca a estos valores y permítame hacerle una pregunta. ¿Puedes determinar cuál será la salida si obtenemos 38 en la entrada?



Si respondiste 100.4, ¡tenías razón!



Entonces, ¿cómo podríamos resolver este problema? Si observa de cerca los valores, puede ver que están relacionados por la expresión:



Donde C - grados Celsius (valores de entrada), F - Fahrenheit (valores de salida).

Lo que acaba de hacer su cerebro: comparó valores de entrada y valores de salida y encontró un modelo común (conexión, dependencia) entre ellos: esto es lo que hace el aprendizaje automático.

Según los valores de entrada y salida, los algoritmos de aprendizaje automático encontrarán un algoritmo adecuado para convertir los valores de entrada en valores de salida. Esto se puede representar de la siguiente manera:



Veamos un ejemplo. Imagine que queremos desarrollar un programa que convierta grados Celsius a grados Fahrenheit usando la fórmula F = C * 1.8 + 32 .



La solución, cuando se aborda desde el punto de vista del desarrollo de software tradicional, se puede implementar en cualquier lenguaje de programación utilizando la función:



Entonces, ¿qué tenemos? La función toma un valor de entrada de C, luego calcula el valor de salida de F usando un algoritmo explícito y luego devuelve el valor calculado.



Por otro lado, en el enfoque de aprendizaje automático, solo tenemos valores de entrada y salida, pero no el algoritmo en sí:



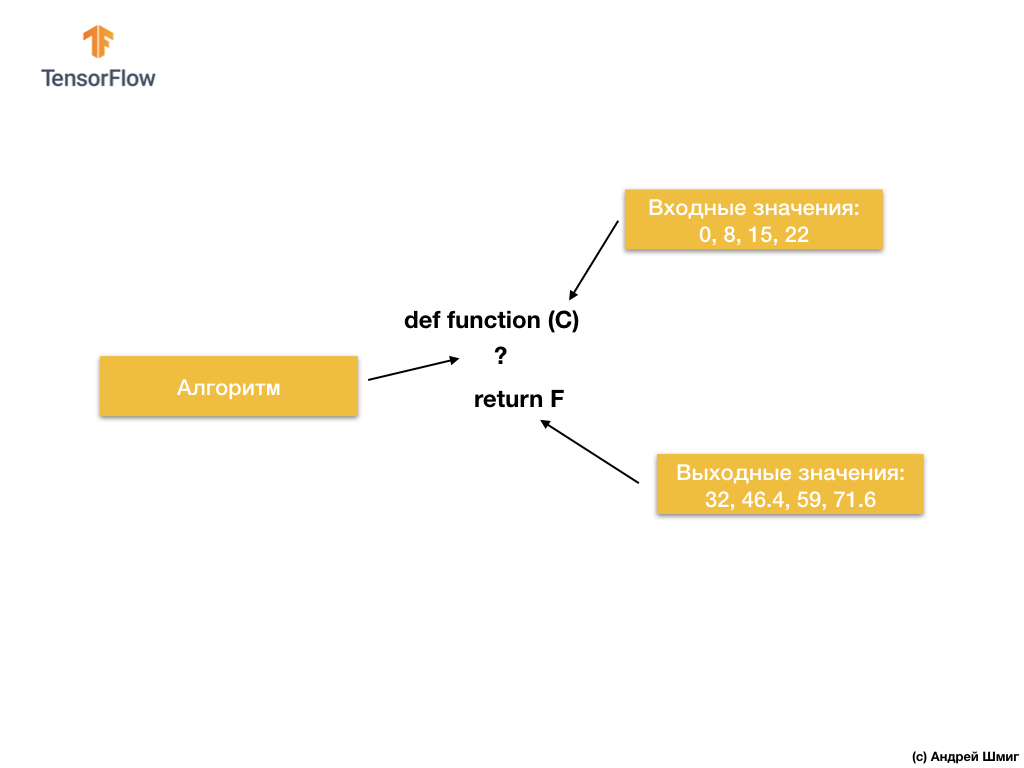
El enfoque de aprendizaje automático se basa en el uso de redes neuronales para encontrar la relación entre los valores de entrada y salida.



Puede pensar en las redes neuronales como una pila de capas, cada una de las cuales consiste en matemáticas (fórmulas) previamente conocidas y variables internas. El valor de entrada ingresa a la red neuronal y pasa a través de una pila de capas de neuronas. Al pasar por las capas, el valor de entrada se convierte de acuerdo con las matemáticas (fórmulas dadas) y los valores de las variables internas de las capas, produciendo un valor de salida.

Para que la red neuronal pueda aprender y determinar la relación correcta entre los valores de entrada y salida, necesitamos entrenarla, entrenar.

Entrenamos la red neuronal a través de intentos repetidos de unir los valores de entrada con los de salida.



En el proceso de entrenamiento, el “ajuste” (selección) de los valores de las variables internas en las capas de la red neuronal ocurre hasta que la red aprende a generar los valores de salida correspondientes a los valores de entrada correspondientes.

Como veremos más adelante, para entrenar una red neuronal y permitirle seleccionar los valores más adecuados de variables internas, se realizan miles o decenas de miles de iteraciones (entrenamientos).



Como una versión simplificada de la comprensión del aprendizaje automático, puede imaginar los algoritmos de aprendizaje automático como funciones que seleccionan los valores de las variables internas para que los valores de entrada correctos correspondan a los valores de salida correctos.

Existen muchos tipos de arquitecturas de redes neuronales. Sin embargo, no importa qué arquitectura elija, las matemáticas internas (qué cálculos se realizan y en qué orden) permanecerán sin cambios durante el entrenamiento. En lugar de cambiar las matemáticas, las variables internas (pesos y compensaciones) cambian durante el entrenamiento.

Por ejemplo, en la tarea de convertir de grados Celsius a Fahrenheit, el modelo comienza multiplicando el valor de entrada por un cierto número (peso) y agregando otro valor (desplazamiento). El entrenamiento modelo consiste en encontrar valores adecuados para estas variables, sin cambiar las operaciones realizadas de multiplicación y suma.

¡Pero una cosa genial para pensar! Si resolvió el problema de convertir grados Celsius a Fahrenheit, que se indica en el video y en el texto a continuación, probablemente lo resolvió porque tenía alguna experiencia o conocimiento previo sobre cómo realizar este tipo de conversión de grados Celsius a Fahrenheit. Por ejemplo, es posible que sepa que 0 grados Celsius corresponden a 32 grados Fahrenheit. Por otro lado, los sistemas basados ​​en el aprendizaje automático no tienen conocimientos previos de respaldo para resolver el problema. Aprenden a resolver estos problemas no basándose en conocimientos previos y en su ausencia total.

Suficiente charla: ¡pase a la parte práctica de la conferencia!

CoLab: convierta grados Celsius a grados Fahrenheit

La versión rusa del código fuente de CoLab y la versión en inglés del código fuente de CoLab .

Lo básico: aprender el primer modelo

¡Bienvenido a CoLab, donde formaremos nuestro primer modelo de aprendizaje automático!

Intentaremos mantener la simplicidad del material presentado e introducir solo los conceptos básicos necesarios para el trabajo. CoLabs posteriores contendrán técnicas más avanzadas.

La tarea que resolveremos es la conversión de grados Celsius a grados Fahrenheit. La fórmula de conversión es la siguiente:

$$

$$f = c \ veces 1.8 + 32$$

Por supuesto, sería más fácil escribir una función de conversión en Python o cualquier otro lenguaje de programación que realizaría cálculos directos, pero en este caso no sería aprendizaje automático :)

En cambio, introducimos en la entrada de TensorFlow nuestros grados de entrada disponibles en grados Celsius (0, 8, 15, 22, 38) y sus grados Fahrenheit correspondientes (32, 46, 59, 72, 100). Luego entrenaremos el modelo de tal manera que corresponda aproximadamente a la fórmula anterior.

Dependencias de importación

Lo primero que importamos es TensorFlow . Aquí y en lo siguiente lo llamamos abreviadamente tf . También configuramos el nivel de registro, solo errores.

A continuación, importe NumPy como np . Numpy nos ayuda a presentar nuestros datos como listados de alto rendimiento.

 from __future__ import absolute_import, division, print_function, unicode_literals import tensorflow as tf tf.logging.set_verbosity(tf.logging.ERROR) import numpy as np 

Preparación de datos de entrenamiento

Como vimos anteriormente, la técnica de aprendizaje automático con el profesor se basa en la búsqueda de un algoritmo para convertir los datos de entrada en salida. Dado que la tarea de este CoLab es crear un modelo que pueda producir el resultado de convertir grados Celsius a grados Fahrenheit, crearemos dos listas: celsius_q y fahrenheit_a , que usaremos al entrenar nuestro modelo.

 celsius_q = np.array([-40, -10, 0, 8, 15, 22, 38], dtype=float) fahrenheit_a = np.array([-40, 14, 32, 46, 59, 72, 100], dtype=float) for i,c in enumerate(celsius_q): print("{}   = {}  ".format(c, fahrenheit_a[i])) 

-40.0 = -40.0
-10.0 = 14.0
0.0 = 32.0
8.0 = 46.0
15.0 = 59.0
22.0 = 72.0
38.0 = 100.0

Algunos términos de aprendizaje automático:

• La propiedad es el valor o valores de entrada de nuestro modelo. En este caso, el valor unitario es grados Celsius.
• Las etiquetas son los valores de salida que predice nuestro modelo. En este caso, el valor unitario es grados Fahrenheit.
• Un ejemplo es un par de valores de entrada-salida utilizados para el entrenamiento. En este caso, este es un par de valores de celsius_q y fahrenheit_a bajo un cierto índice, por ejemplo, (22,72).

Crear un modelo

Luego creamos un modelo. Utilizaremos el modelo más simplificado: el modelo de una red totalmente conectada (red Dense ). Dado que la tarea es bastante trivial, la red también consistirá en una sola capa con una sola neurona.

Construyendo una red

tf.keras.layers.Dense la capa l0 ( l ayer y cero) y la crearemos inicializando tf.keras.layers.Dense con los siguientes parámetros:

• input_shape=[1] : este parámetro determina la dimensión del parámetro de entrada: un valor único. Matriz 1 × 1 con un solo valor. Dado que esta es la primera (y única) capa, la dimensión de los datos de entrada corresponde a la dimensión de todo el modelo. El único valor es un valor de coma flotante que representa grados Celsius.
• units=1 : este parámetro determina el número de neuronas en la capa. El número de neuronas determina cuántas variables de capa interna se utilizarán para entrenar en la búsqueda de una solución al problema. Como esta es la última capa, su dimensión es igual a la dimensión del resultado, el valor de salida del modelo, un único número de punto flotante que representa grados Fahrenheit. (En una red multicapa, el tamaño y la forma de la capa input_shape deben coincidir con el tamaño y la forma de la siguiente capa).

 l0 = tf.keras.layers.Dense(units=1, input_shape=[1]) 

Convertir capas a modelo

Una vez que se definen las capas, deben convertirse en un modelo. Sequential modelo Sequential toma como argumentos la lista de capas en el orden en que deben aplicarse, desde el valor de entrada hasta el valor de salida.

Nuestro modelo tiene una sola capa: l0 .

 model = tf.keras.Sequential([l0]) 

Nota
Muy a menudo, encontrará la definición de capas directamente en la función del modelo, en lugar de su descripción preliminar y uso posterior:

 model = tf.keras.Sequential([ tf.keras.layers.Dense(units=1, input_shape=[1]) ]) 

Compilamos un modelo con una función de pérdida y optimización.

Antes de entrenar, el modelo debe ser compilado (ensamblado). Al compilar para la capacitación, necesita:

• función de pérdida : una forma de medir qué tan lejos está el valor predicho del valor de salida deseado (una diferencia medible se llama "pérdida").
• Función de optimización : una forma de ajustar las variables internas para reducir las pérdidas.

 model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) 

La función de pérdida y la función de optimización se utilizan durante el entrenamiento del modelo ( model.fit(...) mencionado a continuación) para realizar cálculos iniciales en cada punto y luego optimizar los valores.

La acción de calcular las pérdidas actuales y la mejora posterior de estos valores en el modelo es exactamente lo que es el entrenamiento (una iteración).

Durante el entrenamiento, la función de optimización se utiliza para calcular los ajustes a los valores de las variables internas. El objetivo es ajustar los valores de las variables internas de tal manera en el modelo (y esto, de hecho, es una función matemática) para que reflejen lo más fielmente posible la expresión existente para convertir grados Celsius a grados Fahrenheit.

TensorFlow utiliza análisis numérico para realizar este tipo de operaciones de optimización, y toda esta complejidad está oculta a nuestros ojos, por lo que no entraremos en detalles en este curso.

Lo que es útil saber sobre estas opciones:

La función de pérdida (error estándar) y la función de optimización (Adam) utilizadas en este ejemplo son estándar para estos modelos simples, pero hay muchos otros disponibles además de ellos. En esta etapa, no nos importa cómo funcionan estas funciones.

Lo que debe prestar atención es la función de optimización y el parámetro es el coeficiente de learning rate , que en nuestro ejemplo es 0.1 . Este es el tamaño de paso utilizado al ajustar los valores internos de las variables. Si el valor es demasiado pequeño, se necesitarán demasiadas iteraciones de entrenamiento para entrenar el modelo. Demasiado: la precisión cae. Encontrar un buen valor para el coeficiente de tasa de aprendizaje requiere un poco de prueba y error; generalmente se encuentra en el rango de 0.01 (por defecto) a 0.1 .

Nosotros entrenamos el modelo

El entrenamiento del modelo se lleva a cabo por método de fit .

Durante el entrenamiento, el modelo recibe grados Celsius en la entrada, realiza transformaciones utilizando los valores de las variables internas (llamadas "pesos") y devuelve valores que deben corresponder a grados Fahrenheit. Como los valores iniciales de los pesos se establecen arbitrariamente, los valores resultantes estarán lejos de los valores correctos. La diferencia entre el resultado deseado y el real se calcula utilizando la función de pérdida, y la función de optimización determina cómo se deben ajustar los pesos.

Este ciclo de cálculos, comparaciones y ajustes se controla dentro del método de fit . El primer argumento es el valor de entrada, el segundo argumento es el valor de salida deseado. El argumento de las epochs determina cuántas veces se debe completar este ciclo de entrenamiento. El argumento verbose controla el nivel de registro.

 history = model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) print("  ") 

En los siguientes videos, profundizaremos en los detalles de cómo funciona todo esto y cómo exactamente las capas completamente conectadas (capas Dense ) "debajo del capó".

Mostrar estadísticas de entrenamiento

El método de fit devuelve un objeto que contiene información sobre los cambios en las pérdidas con cada iteración posterior. Podemos usar este objeto para construir un programa de pérdidas apropiado. La pérdida alta significa que los grados Fahrenheit predichos por el modelo están lejos de los valores verdaderos en la matriz fahrenheit_a .

Para la visualización, usaremos Matplotlib . Como puede ver, nuestro modelo mejora muy rápidamente al principio, y luego llega a una mejora estable y lenta hasta que los resultados se vuelven "casi" perfectos al final del entrenamiento.

 import matplotlib.pyplot as plt plt.xlabel('Epoch') plt.ylabel('Loss') plt.plot(history.history['loss']) 

Usamos el modelo para las predicciones.

Ahora tenemos un modelo que ha sido entrenado en los valores de entrada celsius_q y valores de salida fahrenheit_a para determinar la relación entre ellos. Podemos usar el método de predicción para calcular los grados Fahrenheit por los cuales previamente no conocíamos los grados Celsius correspondientes.

Por ejemplo, ¿cuánto es 100.0 grados Celsius Fahrenheit? Intenta adivinar antes de ejecutar el siguiente código.

 print(model.predict([100.0])) 

Conclusión

[[211.29639]]


La respuesta correcta es 100 × 1.8 + 32 = 212, ¡así que nuestro modelo funcionó bastante bien!

Revisar

• Creamos un modelo usando la capa Dense .
• La entrenamos con 3.500 ejemplos (7 pares de valores, 500 iteraciones de entrenamiento)

Nuestro modelo ajustó los valores de las variables internas (pesos) en la capa Dense de tal manera que devolviera los valores correctos de grados Fahrenheit a un valor de entrada arbitrario de grados Celsius.

Nos fijamos en los pesos

Vamos a mostrar los valores de las variables internas de la capa Dense .

 print("   : {}".format(l0.get_weights())) 

Conclusión

    : [array([[1.8261501]], dtype=float32), array([28.681389], dtype=float32)] 

El valor de la primera variable está cerca de ~ 1.8, y el segundo de ~ 32. Estos valores (1.8 y 32) son valores directos en la fórmula para convertir grados Celsius a grados Fahrenheit.

¡Esto está realmente muy cerca de los valores reales en la fórmula! Consideraremos este punto con más detalle en los videos posteriores, donde mostraremos cómo funciona la capa Dense , pero por ahora solo necesita saber que una neurona con una sola entrada y salida contiene matemáticas simples: y = mx + b (como una ecuación directo), que no es más que nuestra fórmula para convertir grados Celsius a grados Fahrenheit, f = 1.8c + 32 .

Dado que las representaciones son las mismas, los valores de las variables internas del modelo deben converger a los presentados en la fórmula real, que sucedió al final.

Con la presencia de neuronas adicionales, valores de entrada y valores de salida adicionales, la fórmula se vuelve un poco más complicada, pero la esencia sigue siendo la misma.

Un poco de experimentación

Por diversión! ¿Qué sucede si creamos más capas Dense con más neuronas, que a su vez contendrán más variables internas?

 l0 = tf.keras.layers.Dense(units=4, input_shape=[1]) l1 = tf.keras.layers.Dense(units=4) l2 = tf.keras.layers.Dense(units=1) model = tf.keras.Sequential([l0, l1, l2]) model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) print("  ") print(model.predict([100.0])) print(" ,  100    {}  ".format(model.predict([100.0]))) print("    l0: {}".format(l0.get_weights())) print("    l1: {}".format(l1.get_weights())) print("    l2: {}".format(l2.get_weights())) 

Conclusión

    [[211.74748]]  ,  100    [[211.74748]]       l0: [array([[-0.5972079 , -0.05531882, -0.00833384, -0.10636603]], dtype=float32), array([-3.0981746, -1.8776944, 2.4708805, -2.9092448], dtype=float32)]     l1: [array([[ 0.09127654, 1.1659832 , -0.61909443, 0.3422218 ], [-0.7377194 , 0.20082018, -0.47870865, 0.30302727], [-0.1370897 , -0.0667181 , -0.39285263, -1.1399261 ], [-0.1576551 , 1.1161333 , -0.15552482, 0.39256814]], dtype=float32), array([-0.94946504, -2.9903848 , 2.9848468 , -2.9061244 ], dtype=float32)]     l2: [array([[-0.13567649], [-1.4634581 ], [ 0.68370366], [-1.2069695 ]], dtype=float32), array([2.9170544], dtype=float32)] 

Como habrás notado, el modelo actual también es capaz de predecir bastante bien los grados correspondientes de Fahrenheit. Sin embargo, si observamos los valores de las variables internas (pesos) de las neuronas por capas, entonces no veremos ningún valor similar a 1.8 y 32. La complejidad adicional del modelo oculta la forma "simple" de convertir grados Celsius a grados Fahrenheit.

Manténgase conectado y en la siguiente parte veremos cómo funcionan las capas densas "debajo del capó".

Resumen breve

Felicidades Acabas de entrenar a tu primer modelo. En la práctica, vimos cómo, mediante los valores de entrada y salida, el modelo aprendió a multiplicar el valor de entrada por 1.8 y agregarle 32 para obtener el resultado correcto.



Esto fue realmente impresionante, considerando cuántas líneas de código necesitábamos escribir:

 l0 = tf.keras.layers.Dense(units=1, input_shape=[1]) model = tf.keras.Sequential([l0]) model.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.1)) history = model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False) model.predict([100.0]) 

El ejemplo anterior es un plan general para todos los programas de aprendizaje automático. Utilizará construcciones similares para crear y entrenar redes neuronales y para resolver problemas posteriores.

Proceso de entrenamiento

El proceso de capacitación (que tiene lugar en el método model.fit(...)) consiste en una secuencia muy simple de acciones, cuyo resultado deben ser los valores de las variables internas que dan los resultados lo más cerca posible del original. El proceso de optimización mediante el cual se logran tales resultados, llamado descenso de gradiente , utiliza el análisis numérico para encontrar los valores más adecuados para las variables internas del modelo.

Para participar en el aprendizaje automático, usted, en principio, no necesita comprender estos detalles. Pero para aquellos que todavía están interesados ​​en aprender más: el descenso de gradiente a través de iteraciones cambia un poco los valores de los parámetros, "jalándolos" en la dirección correcta, hasta obtener los mejores resultados. En este caso, "mejores resultados" (mejores valores) significan que cualquier cambio posterior en el parámetro solo empeorará el resultado del modelo. Una función que mide qué tan bueno o malo es el modelo en cada iteración se denomina "función de pérdida", y el objetivo de cada "atracción" (ajuste de valores internos) es reducir el valor de la función de pérdida.

El proceso de entrenamiento comienza con el bloque de "distribución directa", en el que los parámetros de entrada van a la entrada de la red neuronal, siguen las neuronas ocultas y luego van al fin de semana. Luego, el modelo aplica transformaciones internas en los valores de entrada y variables internas para predecir la respuesta.

En nuestro ejemplo, el valor de entrada es la temperatura en grados Celsius y el modelo predijo el valor correspondiente en grados Fahrenheit.



Tan pronto como se predice el valor, se calcula la diferencia entre el valor predicho y el correcto. La diferencia se llama "pérdida" y es una forma de medición de qué tan bien funcionó el modelo. El valor de pérdida se calcula mediante la función de pérdida, que determinamos mediante uno de los argumentos al llamar al método model.compile(...).

Después de calcular el valor de pérdida, las variables internas (pesos y desplazamientos) de todas las capas de la red neuronal se ajustan para minimizar el valor de pérdida con el fin de aproximar el valor de salida al valor de referencia inicial correcto.



Este proceso de optimización se llama descenso de gradiente . Se utiliza un algoritmo de optimización específico para calcular un nuevo valor para cada variable interna cuando se llama al método model.compile(...). En el ejemplo anterior, utilizamos un algoritmo de optimización Adam.

No es necesario comprender los principios del proceso de capacitación para este curso, sin embargo, si tiene curiosidad, puede encontrar más información sobre el Curso acelerado de Google(La traducción y la parte práctica de todo el curso se establecen en los planes de publicación del autor).

En este punto, ya debería estar familiarizado con los siguientes términos:

• Propiedad : valor de entrada de nuestro modelo;
• Ejemplos : pares de entrada + salida;
• Etiquetas : valores de salida del modelo;
• Capas : una colección de nodos unidos dentro de una red neuronal;
• Modelo : representación de su red neuronal;
• Denso y totalmente conectado : cada nodo en una capa está conectado a cada nodo de la capa anterior.
• Pesos y compensaciones : variables internas del modelo;
• Pérdida : la diferencia entre el valor de salida deseado y el valor de salida real del modelo;
• MSE : , , , .
• : , - ;
• : ;
• : «» ;
• : ;
• : ;
• : ;
• Propagación inversa : calcular los valores de las variables internas de acuerdo con un algoritmo de optimización que comienza desde la capa de salida y hacia la capa de entrada a través de todas las capas intermedias.

Capas sensoriales

En la parte anterior, creamos un modelo que convierte grados Celsius a grados Fahrenheit, utilizando una red neuronal simple para encontrar la relación entre grados Celsius y grados Fahrenheit.

Nuestra red consta de una sola capa totalmente conectada. Pero, ¿qué es una capa totalmente conectada? Para resolver esto, creemos una red neuronal más compleja con 3 parámetros de entrada, una capa oculta con dos neuronas y una capa de salida con una sola neurona.



Recuerde que una red neuronal se puede imaginar como un conjunto de capas, cada una de las cuales consiste en nodos llamados neuronas. Las neuronas en cada nivel se pueden conectar a las neuronas de cada capa posterior. El tipo de capas en las que cada neurona de una capa está conectada entre sí a la neurona de la siguiente capa se denomina capa completamente conectada (completamente conectada) o densa (capa Dense).



Por lo tanto, cuando usamos capas completamente conectadas keras, informamos que las neuronas de esta capa deben estar conectadas a todas las neuronas de la capa anterior.

Para crear la red neuronal anterior, las siguientes expresiones son suficientes para nosotros:

 hidden = tf.keras.layers.Dense(units=2, input_shape=[3]) output = tf.keras.layers.Dense(units=1) model = tf.keras.Sequential([hidden, output]) 

Entonces, descubrimos qué son las neuronas y cómo están relacionadas. Pero, ¿cómo funcionan realmente las capas completamente conectadas?

Para comprender lo que realmente está sucediendo allí y lo que están haciendo, debemos mirar "bajo el capó" y desarmar las matemáticas internas de las neuronas.



Imagine que nuestro modelo recibe tres parámetros 1, 2, 3, y 1, 2 3- las neuronas de nuestra red. ¿Recuerdas que dijimos que una neurona tiene variables internas? Por lo tanto, de w * , y b * son la neurona variables más interna, también conocido como el peso y el desplazamiento. Son los valores de estas variables los que se ajustan en el proceso de aprendizaje para obtener los resultados más precisos de comparar los valores de entrada con la salida.



Lo que definitivamente debes tener en cuenta es que las matemáticas internas de la neurona se mantienen sin cambios . En otras palabras, durante el proceso de entrenamiento, solo cambian los pesos y los desplazamientos.

Cuando comienzas a aprender el aprendizaje automático, puede parecer extraño: el hecho de que realmente funciona, ¡pero así es como funciona el aprendizaje automático!

Volvamos a nuestro ejemplo de convertir grados Celsius a grados Fahrenheit.



Con una sola neurona, tenemos solo un peso y un desplazamiento. ¿Sabes que? Esto es exactamente lo que parece la fórmula para convertir grados Celsius a grados Fahrenheit. Si sustituimos el w11valor 1.8, y en lugar de b1- 32, ¡obtenemos el modelo de transformación final!

Si volvemos a los resultados de nuestro modelo desde la parte práctica, prestaremos atención al hecho de que los indicadores de peso y desplazamiento fueron "calibrados" de tal manera que corresponden aproximadamente a los valores de la fórmula.

Creamos a propósito un ejemplo práctico para mostrar claramente la comparación exacta entre pesos y compensaciones. Al poner en práctica el aprendizaje automático, nunca podemos comparar los valores de las variables con el algoritmo de destino de esta manera, como en el ejemplo anterior. ¿Cómo podemos hacer esto? ¡De ninguna manera, porque ni siquiera conocemos el algoritmo objetivo!

Al resolver los problemas del aprendizaje automático, probamos varias arquitecturas de redes neuronales con diferentes números de neuronas en ellas: por ensayo y error encontramos las arquitecturas y modelos más precisos y esperamos que resuelvan el problema en el proceso de aprendizaje. En la siguiente parte práctica, podremos estudiar ejemplos específicos de este enfoque.

Manténgase en contacto, porque ahora comienza la diversión!

Resumen

En esta lección aprendimos enfoques básicos en el aprendizaje automático y aprendimos cómo funcionan las capas completamente conectadas (capas Dense). Entrenó a su primer modelo para convertir grados Celsius a grados Fahrenheit. También aprendió los términos básicos utilizados en el aprendizaje automático, como propiedades, ejemplos, etiquetas. Usted, entre otras cosas, escribió las principales líneas de código en Python, que son la columna vertebral de cualquier algoritmo de aprendizaje automático. Viste que en unas pocas líneas de código puedes crear, entrenar y solicitar una predicción de una red neuronal usando TensorFlowy Keras.

... y un llamado a la acción estándar: regístrese, ponga un plus y comparta :)


YouTube: https://youtube.com/channel/ashmig
Telegram: https://t.me/ashmig
VK: https://vk.com/ashmig