Es bien sabido que la mayoría de las series temporales con las que un investigador tiene que lidiar no son estacionarias, y su análisis es significativamente más complicado que el estudio de procesos estacionarios. Dado que el interés en las wavelets parece haber disminuido, es útil discutir algunos otros instrumentos "no estacionarios" que son principalmente adecuados para estimar frecuencias instantáneas, así como para evaluar espectros instantáneos.
En primer lugar, tiene sentido recordar la "señal analítica". A continuación, el "modelo An" se refiere a la impedancia instantánea y la potencia de la señal de prueba después de completar su parte imaginaria (desplazada en fase por π / 2).
Pero no siempre es posible jugar con la transformación de Gilbert. Anteriormente, ya se
mencionó un método de estimación espectral autorregresiva adecuado para trabajar con secuencias cortas. Aquí, el "modelo AR" se entenderá como el estudio de fragmentos superpuestos cortos (de 5 muestras) de la señal original para determinar los coeficientes de autorregresión de segundo orden, encontrar los "polos" del modelo a partir de ellos, etc.
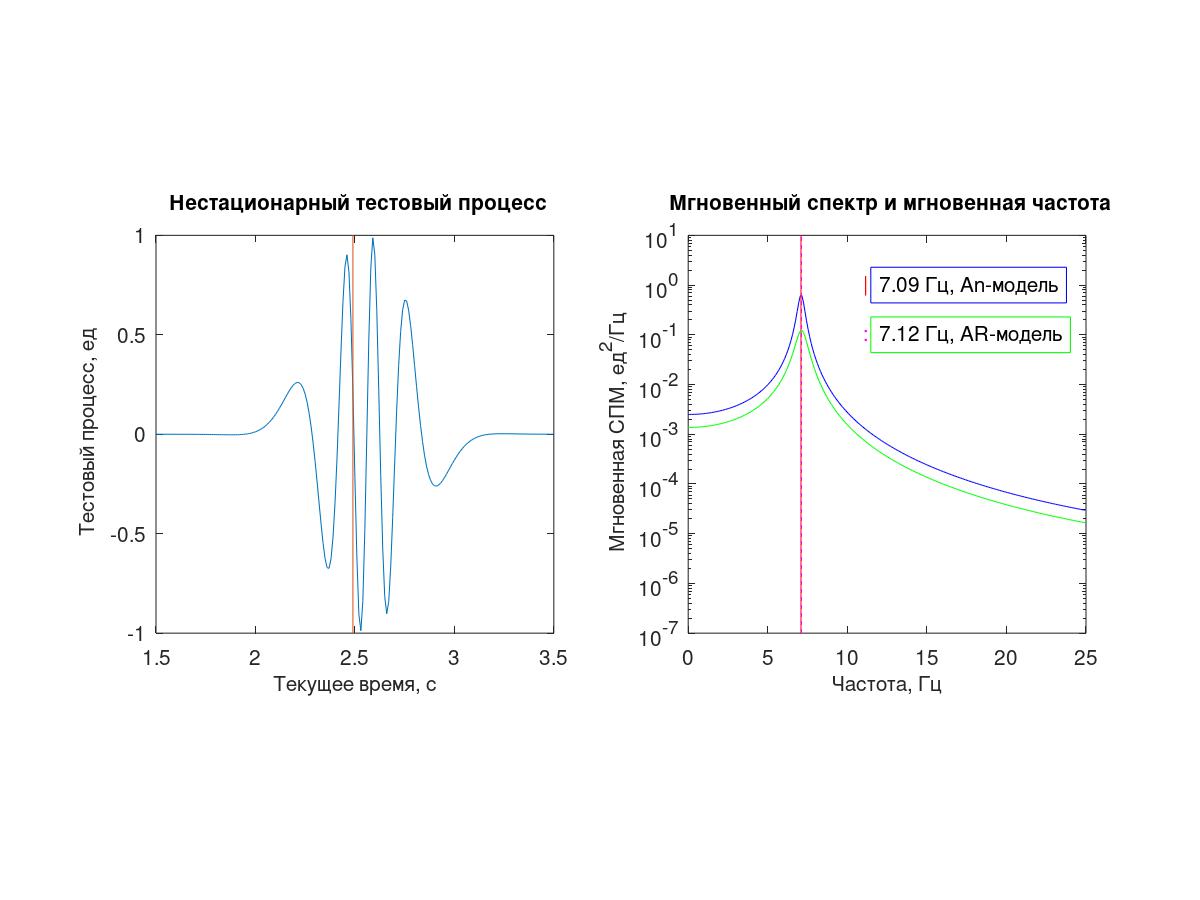

Ambos métodos descritos aquí se basan en un principio: la suposición de que en un pequeño vecindario del momento seleccionado el proceso en estudio puede aproximarse mediante una secuencia "exponencial": un complejo (An) o la suma de dos exponenciales conjugados complejos (AR).
Como proceso de prueba, se utilizó una secuencia de 512 muestras con un intervalo de muestreo condicional Δt = 0.01 s, obtenido de un proceso determinista continuo (1).
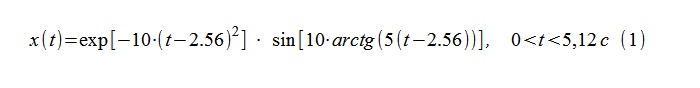
Mediante el "logaritmo" y la posterior diferenciación del relleno de alta frecuencia y la envolvente, respectivamente, de (1), se obtienen expresiones teóricas para la frecuencia y la disminución (instantáneas) (2)

Para el modelado An por el método del periodograma (transformada de Fourier directa e inversa), se genera una señal analítica y [i] a partir de la secuencia inicial x [i].
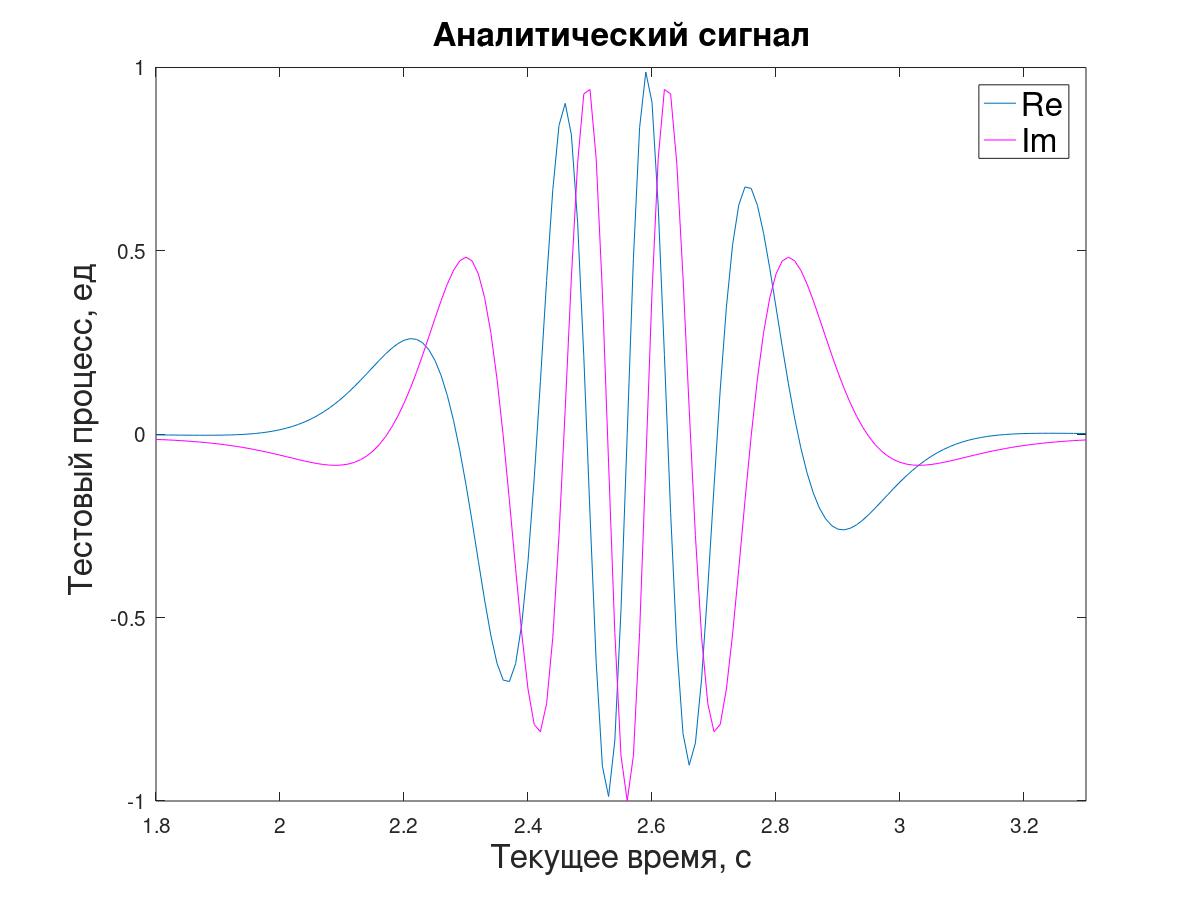
La relación de dos muestras consecutivas de dicha señal, en principio, le permite determinar la impedancia instantánea λ, pero para simplificar esta tarea de demostración, para no molestarse en crear muestras intermedias o explicar el cambio de la estimación en Δt / 2, se decidió trabajar con muestras "a través de una", calculando λ
i con respecto a los valores de señal y [i + 1] posteriores a los y [i-1] anteriores (3).

Para el modelado AR (un modelo de segundo orden), se usó el procedimiento estándar para calcular los coeficientes de autocorrelación 1, a
1i , a
2i usando las ecuaciones de Yule-Walker, y las secuencias de 5 muestras x [i-2], x [i -1], ... x [i + 2] (4).
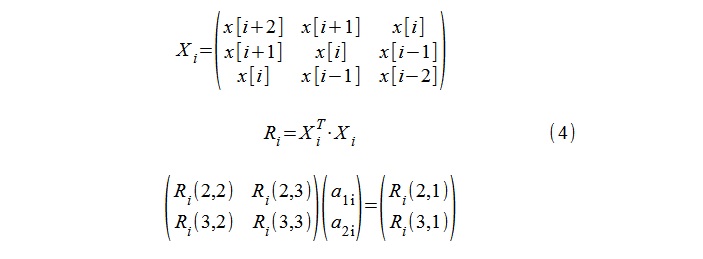
Los "polos" del modelo λ
i se calculan fácilmente mediante el logaritmo de las raíces de la ecuación cuadrática (5).
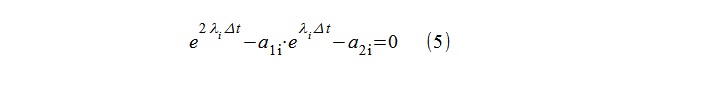

La construcción de estimaciones espectrales a partir de "polos" conocidos hasta un factor de escala
no es
difícil . Siguiente El "poder instantáneo" para el modelo An se define obviamente como | y [i] |
2 , y la cuestión de escalar esta estimación parece estar resuelta. Para el modelo AR, la técnica habitual asociada con la determinación de la potencia del ruido blanco convencional, en el caso de una señal inestable, "no funciona". Por falta de mejores ideas, se aplicó la escala basada en el cuadrado promedio de las 5 muestras correspondientes. Parece que no se puede hacer nada más analizando solo la secuencia de 5 muestras. La animación muestra cómo el gráfico AR de SPM a veces "falla" notablemente en relación con la puntuación An. Debe entenderse que los momentos de la transición "a través de cero" para el modelo AR pueden ser difíciles no solo en términos de errores con frecuencia instantánea, sino también con amplitud instantánea, especialmente en la región de baja frecuencia.
Algunos comentarios al final.
- Por experiencia, ambos métodos generalmente dan buenos resultados para estimar la frecuencia instantánea, al menos en el rango de frecuencia promedio (basado en la frecuencia de muestreo).
- La calidad relativamente alta de los resultados del método An, su simplicidad y facilidad de comprensión e implementación están más que "compensadas" por las posibles dificultades para transformar el proceso según Gilbert. Un filtro digital Gilbert de buena calidad, especialmente en un amplio rango de frecuencia, puede tener un orden inaceptablemente alto. Al implementar un método de periodograma alternativo de esta transformación, se debe tener en cuenta que la transformación de Fourier implica implícitamente la finalización del proceso a periódico. Como resultado, puede ser necesaria una finalización significativa significativa del proceso con ceros. La alta calidad de los resultados del método An se explica por el uso de información en un vecindario muy vasto del instante de tiempo seleccionado (estrictamente hablando, sobre la implementación temporal completa del proceso), y esta misma propiedad dificulta la implementación del método (por ejemplo, cuando se trabaja en tiempo real).
- Si es necesario, se pueden recomendar las siguientes medidas para mejorar los resultados del método AR:
- Reducción de datos (a una frecuencia de muestreo excesivamente alta)
- Un aumento en el número de promedios, una extensión del "momento del tiempo" involucrado en el modelo del vecindario, la construcción de una matriz de pistas X con un gran número de filas.
- Aumentar el orden del modelo AR.