En la ciencia asincrónica, el lugar central está ocupado por la propiedad de los circuitos, llamada independencia de la velocidad, en inglés, independiente de la velocidad (en adelante, SI). Se cree que esta propiedad es un análogo de la independencia de los circuitos asincrónicos de los retrasos de los elementos lógicos. No es sorprendente que el término SI se mencione en casi todos los trabajos sobre asincronía. Pero periódicamente surgen algunas vagas dudas con respecto a este término. No es casualidad que este término sea reemplazado cada vez más por otro término llamado auto-sincronización. Una apelación a la fuente ayudará a aclarar esta situación. Este es el
segundo volumen del libro de La teoría de los circuitos de conmutación de R. Miller, o más precisamente, el Capítulo 10, llamado Teoría de los circuitos de conmutación, independiente de la velocidad.
Entonces, aquí está la definición de circuitos independientes de la velocidad.

Una clase (equivalencia) es un conjunto completo de estados admisibles de un circuito de tal manera que para cualquier estado de este conjunto existe una secuencia de estados admisibles a partir de un estado dado y que contiene todos los estados de un conjunto dado. En otras palabras, desde cualquier estado de una clase puede entrar en cualquier estado de la misma clase.
Una clase (equivalencia) es final si es imposible pasar de los estados de una clase dada a un estado que pertenece a otra clase.
Por ejemplo, todos los patrones de vida (comportamientos) son independientes de la velocidad. Además, no dependen de la velocidad del circuito, que eventualmente se detiene necesariamente, y en un solo estado.
Además, el autor establece una conexión entre los esquemas de SI por un lado, y con los esquemas de distribución semi-modulares y secuenciales por el otro. Y en conclusión, cita una lista de propiedades notables de los circuitos que son independientes de la velocidad.

El primer punto es especialmente interesante. Simplemente dice que los circuitos independientes de la velocidad no dependen de los retrasos de los elementos lógicos. Lamentablemente, el texto no establece explícitamente los motivos de esta conclusión. Tal vez esta sea la razón de los malentendidos posteriores sobre el término SI. En realidad, esta conclusión es completamente cierta. Al comienzo del capítulo 10, el autor proporciona reglas para calcular estados posteriores.

La transición del circuito al siguiente estado es el resultado de cambiar la salida de algún elemento lógico (o las salidas de varios elementos). Es decir, el intervalo de tiempo entre la creación de condiciones para cambiar un elemento lógico (excitación) y su cambio en sí no está limitado por nada. Y ese período de tiempo es un retraso del elemento lógico. Es decir, desde el principio, el autor parte del supuesto de que los retrasos de los elementos lógicos pueden ser arbitrariamente grandes. De hecho, lo siguiente está escrito un poco más.

Bueno, para disipar todas las dudas, una cita de la primera página del capítulo 10.

Por lo tanto, se estableció un hecho indiscutible: la independencia de los retrasos de los elementos lógicos no es una propiedad de un circuito, sino una propiedad del modelo en el que se investiga este circuito. Es decir, cualquier circuito, SI o no SI, investigado de la misma manera descrita por R. Miller, es independiente de los retrasos de los elementos lógicos. Al mismo tiempo, cualquier circuito puede investigarse en un modelo con un retraso limitado. En dicho modelo, el conjunto de estados admisibles es un subconjunto del conjunto de estados admisibles cuando se considera el mismo esquema en un modelo con retraso de elemento ilimitado. Cuando se examina un circuito en un modelo con un retardo de elemento limitado, el circuito puede ser independiente de la velocidad y al mismo tiempo depender de los retrasos del elemento.
Por lo tanto, resulta que la independencia del circuito de los retrasos de los elementos lógicos no está relacionada de ninguna manera con la propiedad SI. Entonces surge la pregunta: ¿cuál es el punto de introducir una definición de independencia de la velocidad? De hecho, considere dos patrones y su comportamiento.
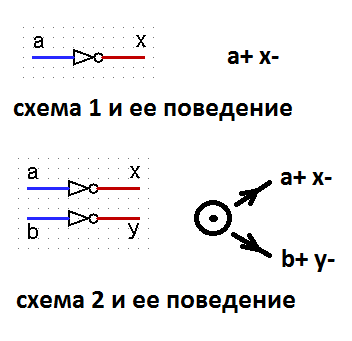
Las señales a, b para ambos circuitos son de entrada, las señales x, y son de salida. Ambos esquemas implementan comportamientos perfectamente razonables. Pero al mismo tiempo, el circuito 1 no depende de la velocidad, y el circuito 2 no tiene esa propiedad. Sí, podemos decir que la definición de SI se introdujo sin dividir las señales en entrada y salida. Pero tal separación de señales por parte del autor estaba implícita, y hay un comentario en el texto sobre esto.
El significado y la razonabilidad de la introducción de la definición de la propiedad SI se revela solo en relación con la propiedad de semi-modularidad. Para circuitos con la propiedad de semi-modularidad, cada señal puede eliminar su excitación solo a través de su conmutación. Los esquemas no semi-modulares durante la implementación física están plagados de fallas y estados metaestables. Solo los esquemas semi-modulares pueden considerarse estables.
Pero la conexión entre las propiedades de semi-modularidad y la independencia de la velocidad es unilateral. Es decir, los esquemas semi-modulares son independientes de la velocidad, pero lo contrario no es cierto. Los circuitos SI pueden no ser semi-modulares. Es decir, una propiedad realmente importante que divide los circuitos según la estabilidad es la semi-modularidad. Es importante comprender que los circuitos semi-modulares también pueden depender de los retrasos de los elementos lógicos, si los consideramos en un modelo con un retraso limitado.
Pero eso no es todo. La propiedad de semi-modularidad también se define para circuitos autónomos, es decir, sin dividir las señales en entrada y salida. Debido a esto, los esquemas de libre elección (comportamientos) no cumplen con los criterios de semi-modularidad. Mientras tanto, estos esquemas pueden ser tan estables como semi-modulares. Por ejemplo, el esquema 2 anterior no es semi-modular, pero en términos de estabilidad, no es de ninguna manera inferior al esquema 1, que es semi-modular.
Hay una salida de este callejón sin salida. El libro J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev "Síntesis lógica para controladores asíncronos e interfaces" define la definición de propiedad de persistencia de salida (OP).

Es la propiedad OP la propiedad real que separa los esquemas (comportamientos) en estable y no estable. Es la propiedad OP la que debe tomar el lugar de la propiedad SI. No debe olvidarse que la independencia de los retrasos de los elementos lógicos es una propiedad del modelo en el que se estudian los circuitos (comportamientos). Y los circuitos OP también pueden depender de los retrasos de los elementos si se consideran en un modelo de retraso limitado.
A pesar de todas las críticas anteriores, no hay quejas contra R. Miller. No hay errores lógicos en su trabajo. La culpa de más de medio siglo de error recae más en los lectores que malinterpretaron el trabajo de R. Miller.
Y finalmente, una conclusión agradable de lo anterior. El modelo de comportamiento STG proporciona un retraso ilimitado para elementos lógicos. Las reglas para cambiar las marcas, extraer la tabla de verdad se formulan a partir del supuesto de elementos de retraso ilimitados. Por lo tanto, cualquier circuito obtenido mediante el cálculo de funciones lógicas usando STG (ya sea usando una tabla de verdad o directamente usando un gráfico) es obviamente independiente de los retrasos de los elementos lógicos. Es cierto que debe entenderse que nuevas manipulaciones con el esquema resultante pueden conducir a la pérdida de esta valiosa calidad.