Todas las descripciones de los cambios son una mezcla única de azar y determinismo, de acuerdo con la prueba radical de la "hipótesis débil" de Pinsker
Imagine un jardín donde crecen todas las flores del mundo: orquídeas delicadas, imponentes girasoles, flores de cera del cactus Carnegie e inflorescencias apestosas del
amorfofalo titánico . Ahora imagine que toda esta diversidad de plantas se ha reducido a solo dos opciones, y que al cruzarlas, puede producir todas las demás.
Esta es la naturaleza de una de las pruebas más radicales obtenidas en los últimos años. Fue hecho por
Tim Austin , un matemático de la Universidad de California en Los Ángeles. Pero en lugar de flores, el trabajo de Austin está asociado con uno de los objetos más estudiados en matemáticas: una descripción matemática de los cambios.
Estas descripciones, conocidas como
sistemas dinámicos , se aplican a todo, desde movimientos planetarios hasta fluctuaciones del mercado de valores. Donde sea que surja un sistema dinámico, los matemáticos quieren entender sus fundamentos. Y uno de los hechos básicos es que cualquier sistema dinámico arbitrariamente complejo puede dividirse en elementos aleatorios y deterministas.
Esta pregunta es el tema de la "hipótesis débil" de Pinsker, que se formuló por primera vez en la década de 1970. La prueba de la hipótesis presentada por Austin proporciona un método elegante e intuitivo de pensar sobre todo tipo de fenómenos oscuros. Mostró que, en esencia, cada uno de estos sistemas dinámicos es una mezcla de azar y determinismo.
Destino y oportunidad
Un sistema dinámico comienza con algunos datos de entrada, por ejemplo, con la posición del péndulo, aplica ciertas reglas, por ejemplo, las leyes de movimiento de Newton, y produce un cierto resultado, por ejemplo, la posición del péndulo en un segundo. Lo que es importante, los sistemas dinámicos le permiten repetir este proceso: puede tomar una nueva posición del péndulo, aplicar las mismas reglas y obtener su posición en otro segundo.
Los sistemas dinámicos también son puramente matemáticos. Puede seleccionar el número inicial, aplicar la regla "multiplique el número por dos" y obtenga uno nuevo. Este sistema también le permite ingresar el número total nuevamente en el controlador de reglas y obtener aún más números.
Ciertos tipos de sistemas dinámicos se pueden expresar como una combinación de dos sistemas dinámicos más simples. Estos dos sistemas funcionan independientemente el uno del otro, pero se pueden combinar para formar uno más complejo. Por ejemplo, imagine un sistema dinámico que mueve un punto a lo largo de la superficie de un cilindro. Usted ingresa la posición del punto, aplica las reglas y obtiene otro punto.
Este sistema se puede desmontar en dos simples. El primero es un sistema dinámico que mueve un punto alrededor de un círculo. El segundo es un sistema que mueve un punto hacia arriba y hacia abajo verticalmente. Al combinar dos sistemas, movimiento circular y movimiento recto, obtenemos un movimiento puntual más complejo a lo largo del cilindro.
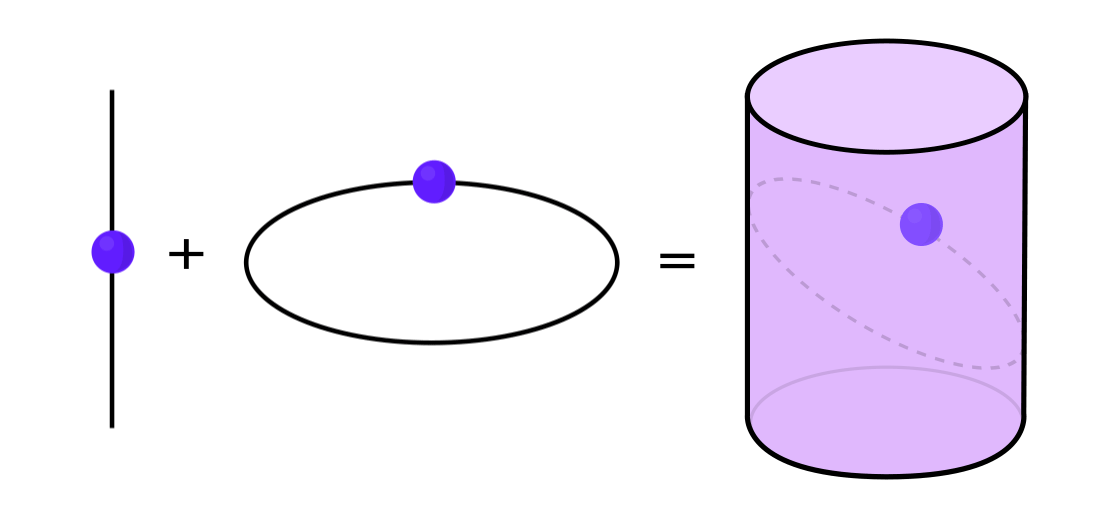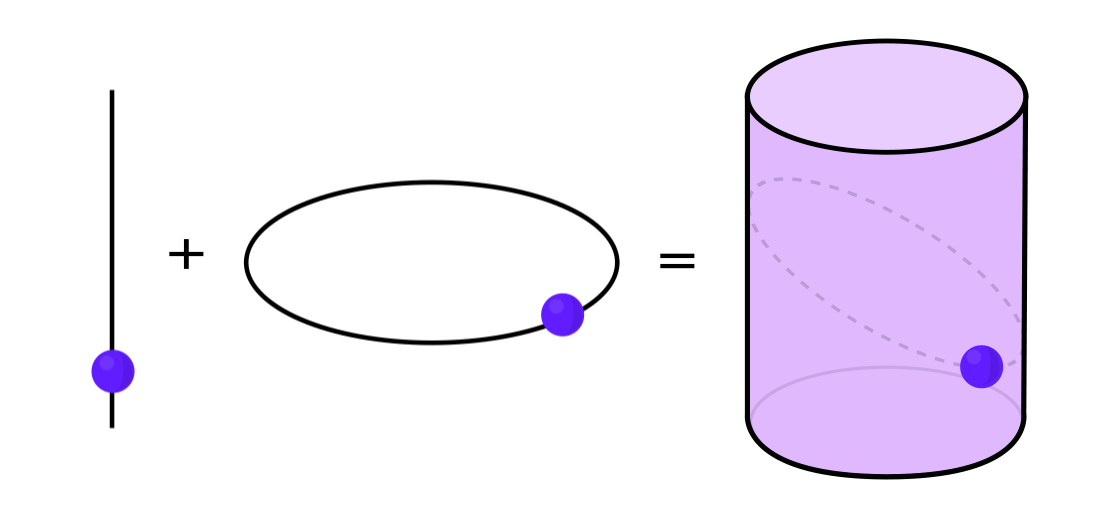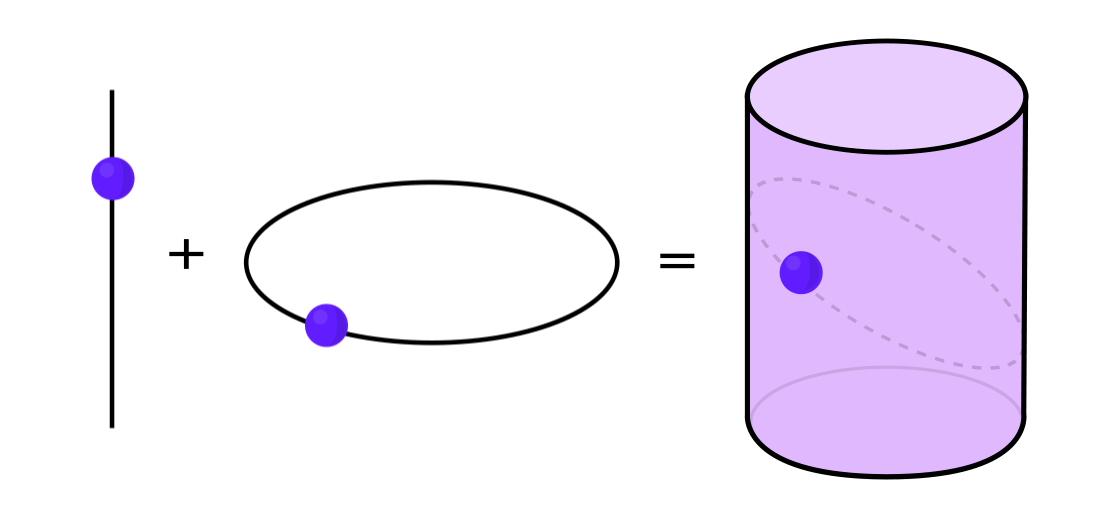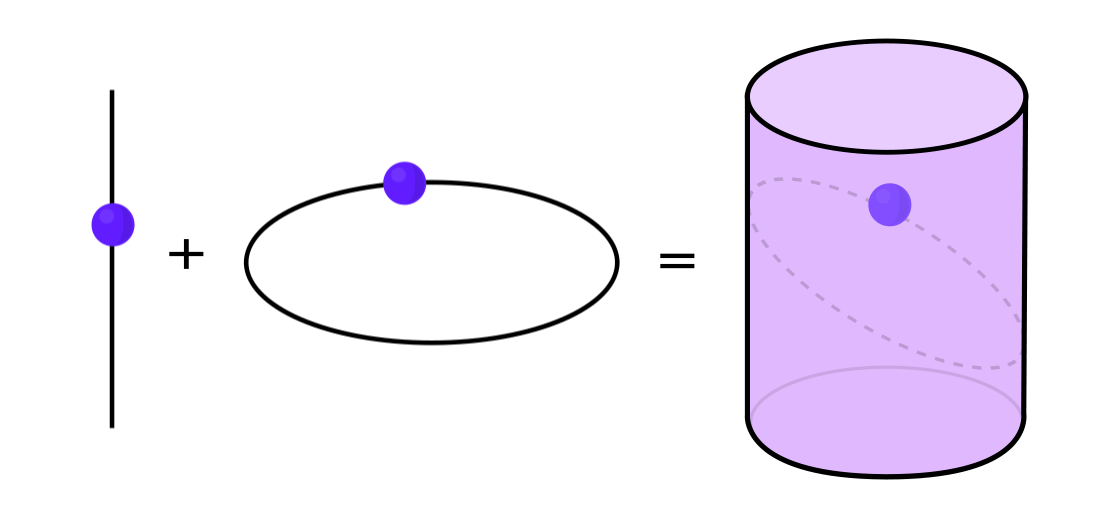
"En lugar de estudiar todo el sistema dinámico en su totalidad, debe dividirlo en partes, pequeñas partes que tengan sentido para estudiar", dijo
Catherine Lindsay , matemática del Boston College.
Hay dos candidatos naturales para el papel de estos bloques de construcción. Los primeros son sistemas dinámicos totalmente deterministas, como nuestro ejemplo de péndulo. Si conoce la posición del péndulo en algún momento, puede predecirlo en cualquier momento en el futuro.
 Jean-Paul Tuveno en 1975, dos años antes de la formulación de la débil hipótesis de Pinsker
Jean-Paul Tuveno en 1975, dos años antes de la formulación de la débil hipótesis de PinskerEl segundo tipo de sistemas dinámicos es completamente aleatorio. Por ejemplo, imagine un sistema dinámico con esta regla: lanzar una moneda. Si hay un águila, da un paso a la izquierda; Si las colas, a la derecha. La ruta final será completamente aleatoria, es decir, incluso si sabe todo sobre la ruta anterior, esta información no lo ayudará a predecir el siguiente paso.
Algunos sistemas dinámicos son completamente aleatorios, otros son completamente deterministas y la mayoría están en algún punto intermedio: son un híbrido de ambos. Por ejemplo, imagine una versión ligeramente modificada de nuestra caminata aleatoria. Caminamos por un camino a lo largo del borde del cual se plantan flores, y sus colores también son aleatorios. La regla sigue siendo la misma: si cae un águila, ve a la izquierda; Si las colas, a la derecha. ¿Cuál será la secuencia de colores de flores?
Primero dices al azar. Después de todo, los colores mismos fueron elegidos al azar, y tu movimiento también es aleatorio. Sin embargo, después de haber pasado una sola flor, aumenta la probabilidad de que la pase en el futuro, simplemente porque no está lejos de ella. La secuencia de colores de las flores no será completamente al azar.
"Si te paras al lado del rojo, aumenta las posibilidades de que en dos pasos te encuentres con el rojo nuevamente, porque puede suceder que pises a la izquierda, luego a la derecha y regreses al mismo lugar", dijo Austin.
Tal "paseo aleatorio a través de un paisaje aleatorio" produce resultados, una secuencia de colores, en parte aleatoria y en parte no. En 1960, el matemático Mark Pinsker sugirió que cierta clase grande de sistemas dinámicos tiene la siguiente propiedad: son una mezcla de un sistema dinámico aleatorio con uno determinista.
La conjetura de Pinsker es aplicable a la clase de sistemas dinámicos que tienen una propiedad común importante. Los puntos en ellos no se alejan entre sí y no se reducen durante el desarrollo del sistema. Más precisamente, si dibuja un bucle alrededor de un conjunto de puntos en su espacio (el espacio puede ser algo así como una superficie cilíndrica), comience el desarrollo de un sistema dinámico durante un largo período de tiempo y luego dibuje un bucle alrededor del conjunto de puntos resultante, luego el área en la que los puntos final, coincide con el área que ocuparon al principio. Dichos sistemas se denominan "preservación de medidas"
"Si la hipótesis original de Pinsker fuera cierta, sería una descripción sorprendente del mundo", dijo
Assaf Naor , matemático de la Universidad de Princeton. Pero Pinsker estaba equivocado. En 1973,
Donald Ornstein refutó su hipótesis. "La redacción era demasiado ambiciosa", dijo
Brina Kra , matemática de la Universidad Northwestern.
En matemáticas, a menudo sucede que después de que se refuta la hipótesis general, los matemáticos intentan formular una versión más modesta de la misma. En 1977, el matemático Jean-Paul Tuveno propuso la débil hipótesis de Pinsker. Suavizó la formulación original, sugiriendo que los sistemas dinámicos que Pinsker tenía en mente eran el resultado de combinar un sistema puramente aleatorio con un sistema que era casi completamente determinista.
El refinamiento "casi" distingue la hipótesis de Tuveno de la hipótesis de Pinsker. Se refería a que un sistema determinista simple debería tener alguna posibilidad de azar. Este rastro puede estar desapareciendo pequeño, pero debería estar allí. Y mientras lo esté, dijo Tuveno, la idea de Pinsker funcionará.
"Estaba cerca de la hipótesis original, y Tuveno demostró que si es así, entonces la hipótesis tendrá una gran cantidad de excelentes aplicaciones", dijo Naor.
En las décadas siguientes, los matemáticos no lograron mucho éxito al probar la débil hipótesis de Pinsker. La falta de progreso hizo que Tuveno pensara que incluso su redacción debilitada resultaría estar equivocada. "En un momento, pensé que todo sería lo contrario, que no sería universal", dijo.
Y entonces apareció Tim Austin.
Solución escalonada
Para probar la débil hipótesis de Pinsker, era necesario encontrar una forma exacta de examinar un sistema dinámico, uno que le permitiera separar sus partes aleatorias y casi deterministas. El trabajo previo ha establecido que será más difícil aislar elementos con un poco de aleatoriedad.
"Los factores aleatorios pequeños son mucho más difíciles de atrapar, y la parte central de la evidencia es encontrar una forma de detectar una estructura aleatoria pequeña", dijo Tuveno.
 Tim Austin, matemático de la Universidad de California, Los Ángeles.
Tim Austin, matemático de la Universidad de California, Los Ángeles.Austin logró lidiar con pequeños elementos aleatorios de un sistema dinámico cambiando las perspectivas. Los sistemas dinámicos operan en un espacio continuo, como un punto que se mueve a lo largo de la superficie de un cilindro o un péndulo que se balancea en el espacio. En estos espacios, los puntos se mueven a lo largo de arcos continuos de acuerdo con las reglas de un sistema dinámico. Además, estos sistemas funcionan en un número infinito de pasos: pueden actuar para siempre.
Pero en su prueba, Austin abandonó el espacio continuo continuo y se olvidó del trabajo eterno de los sistemas dinámicos. En cambio, comenzó a analizar qué sucedería si se les permitiera trabajar en momentos discretos, como un millón de pasos. Así aplicó el método inventado por Tuveno.
"La principal contribución de Tuveno fue que se dio cuenta de que si realiza los pasos matemáticos correctos con líneas finitas largas, puede probar las propiedades de un sistema dinámico", dijo Austin. "Mi contribución principal fue que probé lo que se necesitaba para las líneas finales largas".
Austin imaginó un sistema dinámico emitiendo una secuencia de unos y ceros. Si el sistema dinámico está lanzando una moneda, entonces es fácil de imaginar: las colas serán 1 y las cabezas serán 0. Pero cualquier sistema dinámico puede usarse para generar una secuencia binaria simplemente dividiendo el espacio en el que funciona en dos (no necesariamente igual) partes
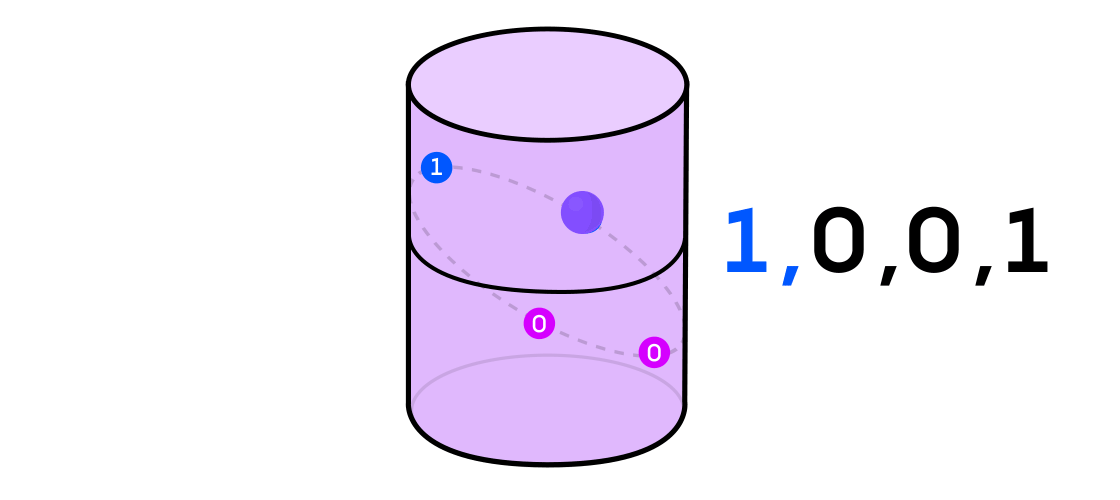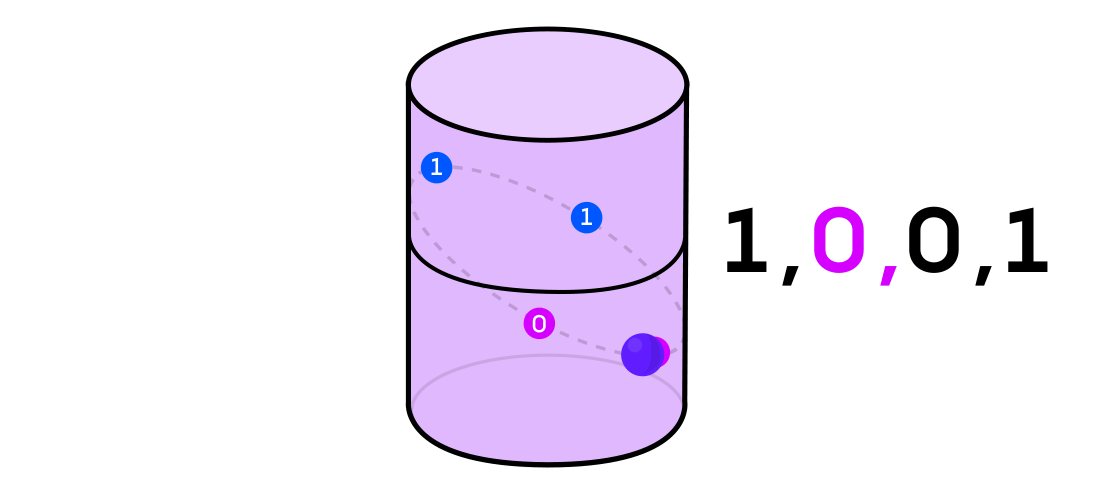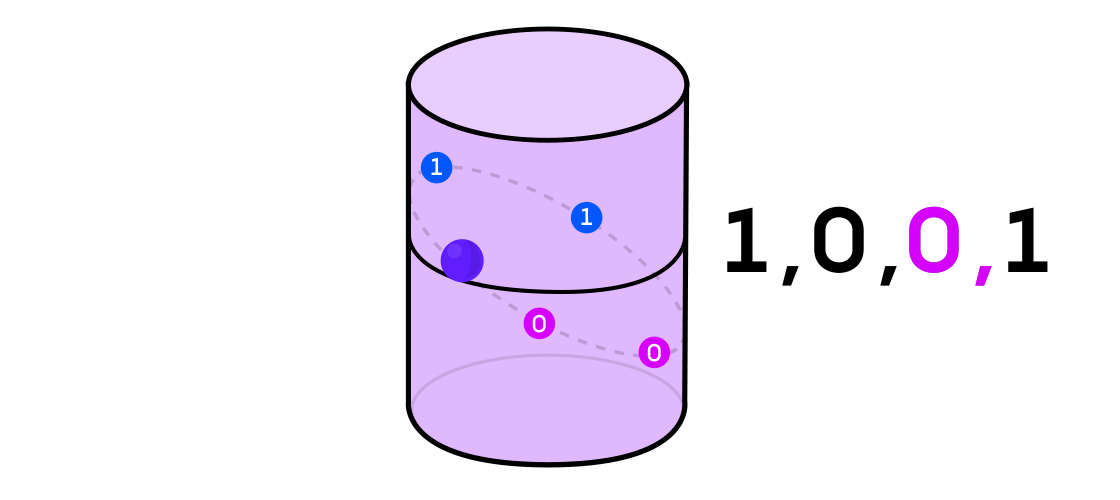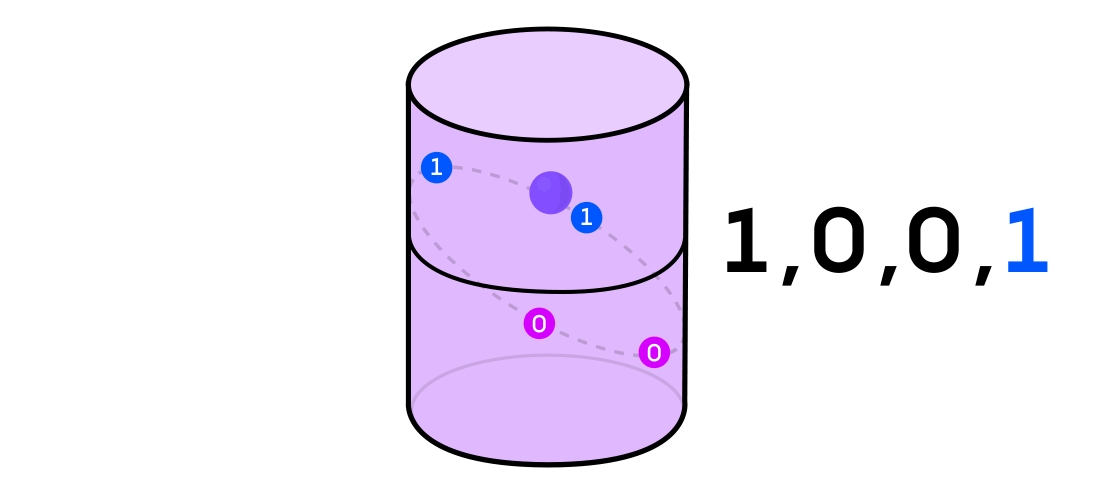
Volviendo al ejemplo de un sistema dinámico en un cilindro, si el punto está en una parte del cilindro, denota el valor de salida del sistema 1, y si en la otra, entonces 0.
Austin analizó estas secuencias binarias usando una herramienta de
teoría de la información llamada
Hamming Cubes . Imagina un cubo de vértices conectados por bordes. Se asignan números binarios a cada vértice, por ejemplo, 001 o 101. Cada vez, al cambiar de un vértice a otro, cambia uno de los tres dígitos.
Los cubos de Hamming pueden ser mucho más complicados que los nuestros, pueden tener tantos bordes y vértices más en más dimensiones que tres, pero todos tienen la propiedad, debido a que la distancia entre dos vértices, o la cantidad de bordes que necesita recorrer ir de un vértice a otro es igual al número de lugares en los que se distinguen las líneas de información correspondientes a estos vértices. Por lo tanto, 000 se encuentra a la distancia de un borde desde 001, dos bordes desde 011 y tres desde 111.

Para aislar los elementos aleatorios y deterministas que conforman un sistema dinámico complejo, Austin pensó en la frecuencia con que un sistema dinámico puede producir una secuencia dada de ceros y unos representados en un cubo de Hamming. Él demostró que estas secuencias se distribuyen en un cubo de cierta manera. Se acumulan en un pequeño número de subregiones de cubos, y este grupo refleja el determinismo del sistema, sin embargo, se distribuyen aleatoriamente entre las secuencias dentro de estos grupos, lo que refleja la aleatoriedad del sistema.
Tal rotonda era necesaria para resolver un problema que no cedía a los ataques directos.
"Lo que me sorprendió no fue tanto la verdad o la falsedad de la débil hipótesis de Pinsker, sino cómo resultó probar, porque esta tarea parecía tan insidiosa", dijo Lewis Bowen, matemático de la Universidad de Texas en Austin. "Antes de que apareciera la evidencia, nosotros, en general, no teníamos idea de si esto podía hacerse en absoluto".
El resultado de Austin da la estructura básica a una amplia gama de sistemas dinámicos. Para los matemáticos, que a menudo giran entre objetos que parecen interconectados, no está claro cómo la prueba proporciona su geografía exacta. Ahora tienen una guía para estos sistemas dinámicos, aunque aún se desconoce a qué tipo de descubrimientos llevará esto.
"Los matemáticos siempre están interesados en los componentes básicos que componen cualquier cosa", dijo Lindsay. "La prueba de Austin es un resultado excelente, que probablemente tenga muchas aplicaciones en matemáticas puras, pero no puedo decir cuáles serán".