👩🏾‍🤝‍👨🏿 👨🏼‍🎤 🐳 Análisis de wavelet. Parte 3 🤦🏻 🔹 🚂

Introduccion

Cuando se realiza un análisis CWT utilizando la biblioteca PyWavelets (un software gratuito de código abierto lanzado bajo la licencia MIT), existen problemas para visualizar el resultado. El programa de prueba de visualización propuesto por los desarrolladores se muestra en la siguiente lista:

Listado

import pywt import numpy as np import matplotlib.pyplot as plt t = np.linspace(-1, 1, 200, endpoint=False) sig = np.cos(2 * np.pi * 7 * t) + np.real(np.exp(-7*(t-0.4)**2)*np.exp(1j*2*np.pi*2*(t-0.4))) widths = np.arange(1, 31) cwtmatr, freqs = pywt.cwt(sig, widths, 'cmor1-1.5') plt.imshow(cwtmatr, extent=[-1, 1, 1, 31], cmap='PRGn', aspect='auto', vmax=abs(cwtmatr).max(), vmin=-abs(cwtmatr).max()) # doctest: +SKIP plt.show() # doctest: +SKIP

Cuando se trabaja con wavelets complejas, por ejemplo con 'cmor1-1.5', el programa produce un error:

 File"C:\Users\User\AppData\Local\Programs\Python\Python36\lib\site-packages\matplotlib\image.py", line 642, in set_data raise TypeError("Image data cannot be converted to float") TypeError: Image data cannot be converted to float

Este error, así como las dificultades para elegir la escala (anchos) para proporcionar la resolución de tiempo necesaria, dificultan, especialmente para los usuarios novatos, estudiar el análisis de CWT, lo que me llevó a escribir este artículo de naturaleza educativa.

El propósito de esta publicación es considerar el uso del nuevo módulo de visualización de escalagrama para el análisis de señales simples y especiales, así como cuando se utilizan métodos de normalización, escalamiento logarítmico y síntesis, que proporcionan información adicional en el análisis de series de tiempo.

El artículo utilizó información de la publicación "Una introducción suave a wavelet para el análisis de datos" . En los listados de ejemplos dados en la publicación, los errores se corrigen y cada listado del ejemplo se lleva a su forma final, lo que le permite usarlo sin familiarizarse con los anteriores. Para el análisis wavelet de señales especiales, se utilizaron datos de la base de datos de muestra PyWavelets.

Un escalograma wavelet es una representación bidimensional de datos unidimensionales. El tiempo se traza en el eje X, y se muestra una escala en el eje Y, el resultado de la transformada wavelet de la señal correspondiente a la amplitud de la señal en el tiempo X. El valor analítico de tal visualización gráfica de la señal es que la resolución del tiempo se muestra en el eje Y, que proporciona información adicional sobre las propiedades dinámicas de la señal.

Wavelet - Escalogramas de señal simple

1. Onda cosenoidal con una envoltura gaussiana (Reemplazo de wavelets. Puede estudiar la dependencia de la resolución del tiempo en la escala)

Listado

 from numpy import* from pylab import* import scaleogram as scg import pywt #  ,        #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) p1=10; periodic1 = cos(2*pi/p1*time) * exp(-((time-ns/2)/200)**2) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(periodic1); ax1.set_xlim(0, len(time)) ax1.set_title("   ") fig1.tight_layout() ax2 = scg.cws(periodic1, scales=scales, figsize=(6.9,2.9)); txt = ax2.annotate("p1=%s"%p1, xy=(100, 10), bbox=dict(boxstyle="round4", fc="w")) tight_layout() print("    :", scg.get_default_wavelet(), "(", pywt.ContinuousWavelet(scg.get_default_wavelet()).family_name, ")") show()

Función wavelet para conversión de señal: cmor1-1.5 (wavelets complejas de Morlet)

La señal periódica ahora aparece como una franja continua horizontal en el punto Y = p1, cuya intensidad varía según la amplitud de la señal periódica.

Hay algo de confusión en la detección, ya que el ancho de banda no es igual a cero, esto se debe al hecho de que las wavelets no detectan una frecuencia, sino más bien una banda. Este efecto está asociado con el ancho de banda de wavelet.

2. Se agregan tres pulsos secuencialmente con un período creciente (para considerar variaciones periódicas a diferentes escalas: análisis de resolución múltiple):

Listado

 from numpy import* import pandas as pd from pylab import* import scaleogram as scg #          #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) pulses = zeros(ns, dtype=float32) steps = linspace(0, ns, 8) periods = [10, 20, 40] for i in range(0,3): step_mask = (time > steps[i*2+1]) & (time < steps[i*2+2]) pulses += cos(2*pi/periods[i]*time) * step_mask fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(pulses); ax1.set_xlim(0, len(time)); ax1.set_title("     "); ax1.set_xlabel("Time") fig1.tight_layout() ax2 = scg.cws(pulses, scales=scales, figsize=(7,3)) for i in range(0, 3): txt = ax2.annotate("p%d=%ds"%(i+1,periods[i]), xy=(steps[i*2]+20, periods[i]), bbox=dict(boxstyle="round4", fc="w")) ax2.plot(steps[i*2+1]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) ax2.plot(steps[i*2+2]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) tight_layout() show()

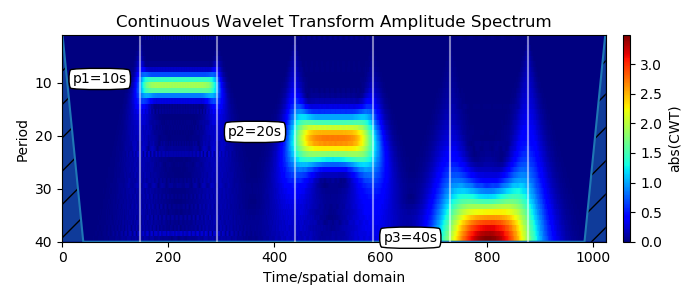
Los impulsos aparecen en el lugar esperado Y, correspondiente a su periodicidad, se localizan en frecuencia y tiempo. El comienzo de la tira y el final corresponden al impulso.
El ancho de banda se escala con la duración del período. Esta es una propiedad bien conocida de la transformada wavelet: cuando la escala aumenta, la resolución del tiempo disminuye. Esto también se conoce como el equilibrio entre tiempo y frecuencia. Cuando miras un espectrograma de este tipo, haces muchos análisis de resolución.

3. Tres oscilaciones periódicas de diferentes frecuencias al mismo tiempo (Wavelet: el análisis puede distinguir los componentes de la señal por frecuencia, si sus diferencias son significativas):

Listado

 from numpy import* import pandas as pd from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) allwaves = np.zeros(ns, dtype=np.float32) periods = [10, 20, 40] for i in range(0,3): allwaves += cos(2*np.pi/periods[i]*time) fig1, ax1 = subplots(1, 1, figsize=(6.5,2)); lines = ax1.plot(allwaves); ax1.set_title("  ") ax1.set_xlim(0, len(time)); ax1.set_xlabel("") fig1.tight_layout() ax2 = scg.cws(allwaves, scales=scales, figsize=(7,2)) tight_layout() show()

4. Una señal periódica no sinusoidal (se considera la diferencia en las transformaciones de wavelet de una señal de onda triangular con un período de 30 segundos de las consideradas anteriormente):

Listado

 from numpy import* from pylab import* import scipy.signal import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) ptri = 30.0 # period in samples raising = 0.8 # fraction of the period raising triangle = scipy.signal.sawtooth(time/ptri*2*pi, raising) # plot the signal fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(triangle); ax1.set_xlim(0, len(time)) ax1.set_title("triangle wave increasing 80% of the time with a 30s period") fig1.tight_layout() # and the scaleogram ax2 = scg.cws(triangle, scales=scales, figsize=(7,3)); txt = ax2.annotate("first harmonic", xy=(100, 30), bbox=dict(boxstyle="round4", fc="w")) txt = ax2.annotate("second harmonic", xy=(100, 15), bbox=dict(boxstyle="round4", fc="w")) tight_layout() show()

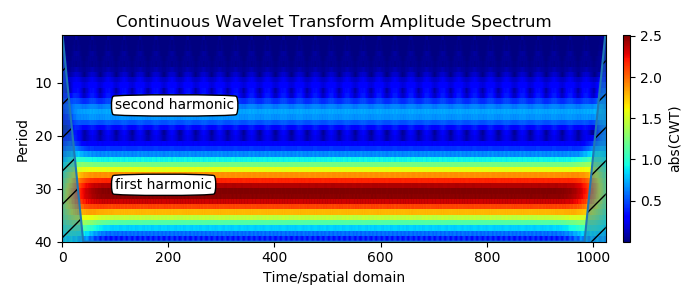
Una banda grande es el primer armónico. El segundo armónico es visible exactamente a la mitad del valor del período del primer armónico. Este es el resultado esperado para señales periódicas no sinusoidales. Aparecen elementos verticales difusos alrededor del segundo armónico, que es más débil y tiene una amplitud de 1/4 del primero para una forma de onda triangular.

5. Los impulsos suaves (gaussianos) son similares a las estructuras de datos reales. (Este ejemplo muestra cómo usar el análisis wavelet para detectar cambios de señal localizados a lo largo del tiempo):

Una serie de pulsos suaves con diferentes valores sigma:

$2 \ cdot \ sigma _ {1} = 2$
$2 \ cdot \ sigma _ {2} = 10$
$2 \ cdot \ sigma _ {3} = $ 2$

Ancho de pulso:

$\ omega _ {1} = 2$
$\ omega _ {2} = $ 2$
$\ omega _ {3} = $ 10$

Listado

 from numpy import* from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) #       s1=1; s2=5; s3=10 events = [ns*0.1, ns*0.3, ns*0.7] bumps = exp(-((time-events[0])/s1)**2) + exp(-((time-events[1])/s2)**2) + \ exp(-((time-events[2])/s3)**2) #      w1=1; w2=5; w3= 50 steps = ((time > events[0]-w1) & (time < events[0]+w1)) + \ ((time > events[1]-w2) & (time < events[1]+w2)) + \ ((time > events[2]-w3) & (time < events[2]+w3)) #   fig1, (ax1, ax2) = subplots(1, 2, figsize=(11, 2)); ax1.set_title("Bumps"); ax2.set_title("Steps") lines = ax1.plot(bumps); ax1.set_xlim(0, len(time)) lines = ax2.plot(steps); ax2.set_xlim(0, len(time)) fig1.tight_layout() #   scales_bumps = scg.periods2scales(arange(1, 120, 2) ) fig2, (ax3, ax4) = subplots(1, 2, figsize=(14,3)); ax3 = scg.cws(bumps, scales=scales_bumps, ax=ax3) ax4 = scg.cws(steps, scales=scales_bumps, ax=ax4) for bmpw, stepw in [(2*s1, 2*w1), (2*s2,2*w2), (2*s3, 2*w3)]: ax3.plot(ax3.get_xlim(), bmpw*ones(2), 'w-', alpha=0.5) ax4.plot(ax4.get_xlim(), stepw*ones(2), 'w-', alpha=0.5) fig2.tight_layout() show()

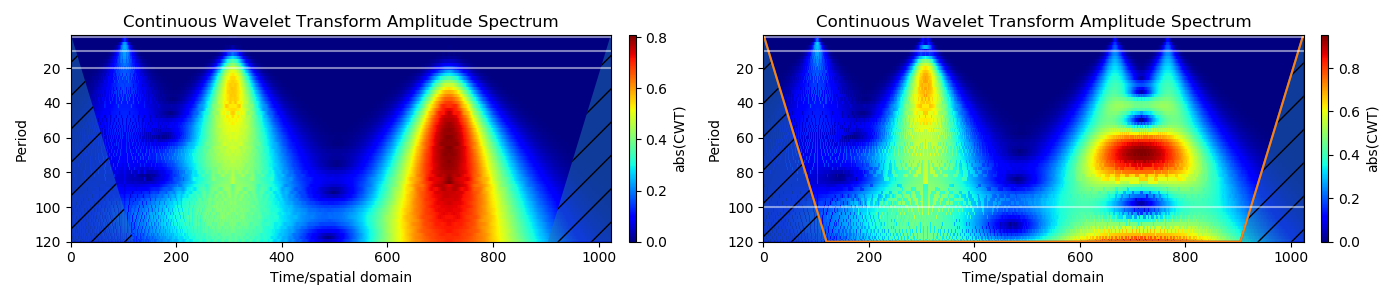
Los pulsos discretos crean estructuras cónicas en el sialograma, que también se conocen como el cono de influencia. Los impulsos suaves (gaussianos) son similares a las estructuras de datos reales y crean conos que se expanden hacia grandes escalas. Las líneas de guía horizontales corresponden aproximadamente a períodos de tiempo (2 s, 10 s, 20 s). Por lo tanto, el pulso es similar a una señal periódica con un período.

6. Ruido (ruido de pantalla en el sialograma):

Listado

 from numpy import* from pylab import* import scaleogram as scg import random scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) noise =random.sample(range(ns), ns) fig1, ax1 = plt.subplots(1, 1, figsize=(6.2,2)); ax1.set_title("  ") lines = ax1.plot(time, noise) ax1.set_xlim(0, ns) fig1.tight_layout() ax2 = scg.cws(noise, scales=scales, figsize=(7,2)) tight_layout() show()

El ruido generalmente se muestra como un conjunto de elementos, y algunas irregularidades pueden parecer objetos de datos reales, por lo que al usar datos reales, debe tener cuidado y, si es necesario, verificar el nivel de ruido. El horario superior será diferente cada vez que se inicie el programa.

Escalogramas Wavelet de Señales Especiales

La base de datos PyWavelets contiene veinte señales especiales de transformación wavelet que serán útiles tanto para el estudio como para el desarrollo. Por lo tanto, le daré una lista que le permite realizar un análisis wavelet de las veinte señales:

Listado

 #!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from pylab import* import scaleogram as scg import pywt signals = pywt.data.demo_signal('list') signal_length=1024 for signal in signals: if signal in ['Gabor', 'sineoneoverx']: x = pywt.data.demo_signal(signal) else: x = pywt.data.demo_signal(signal, signal_length) times=[] signals=[] for time, sig in enumerate(x.real): times.append(time) signals.append(sig) scg.set_default_wavelet('cmor1-1.5') scales = scg.periods2scales( arange(1, 40) ) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(signals); ax1.set_xlim(0, len(times)) ax1.set_title("%s"%signal) fig1.tight_layout() ax2 = scg.cws(signals, scales=scales, figsize=(6.9,2.9)); tight_layout() show()

Solo daré un resultado de la transformada wavelet de la señal Doppler:

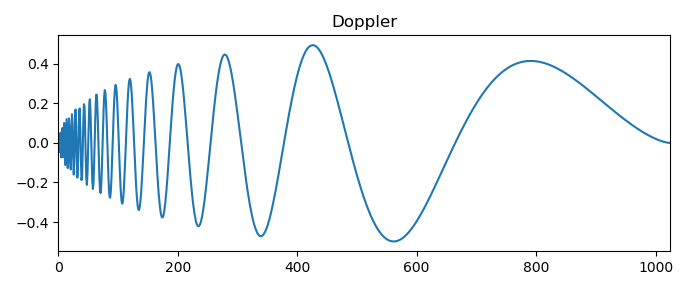
Se consideran las variedades más comunes de señales simples y especiales, lo que nos permite pasar a usar un escalograma para resolver algunos problemas de análisis de series temporales.

Escalogramas de línea de tiempo de wavelet

1. Datos de fertilidad de los CDC en los Estados Unidos 1969-2008 (los datos de fertilidad contienen características periódicas, tanto en una escala anual como en una más pequeña):

Listado

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) fig = figure(figsize=(12,2)) lines = plot(births.index, births.values/1000, '-') xlim(datetime_lim) ylabel("Nb of birthes [k]"); title("Total births per day in the US (CDC)"); xlim = xlim() ax = scg.cws(births, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()

Aparece una línea horizontal con una frecuencia de aproximadamente 7 días. Los valores altos aparecen cerca de los bordes de la escala, que es el comportamiento normal del procesamiento de wavelets. Estos efectos son bien conocidos como un cono de influencia, por lo que una máscara (opcional) se superpone a esta área.

2. Normalización (Eliminar el valor promedio - births_normed = births-births.mean () es obligatorio, de lo contrario, los límites de datos se consideran etapas que crean muchas detecciones falsas en forma de cono):

Listado

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() ax = scg.cws(births_normed, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()

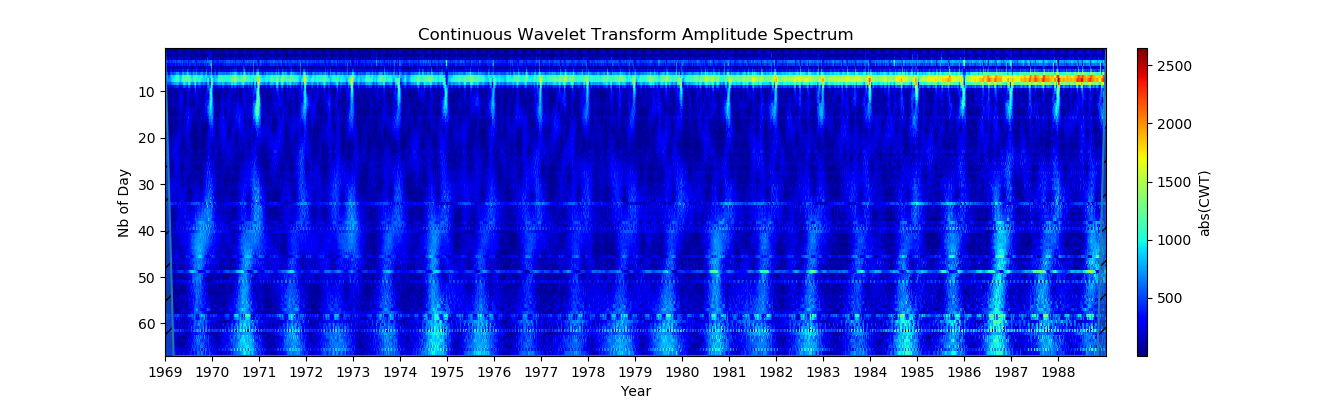
3. Cambio de escala en amplitud (para ver objetos anuales, usando period2scales () se especifica la escala a lo largo del eje Y).

Listado

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 5), xlabel="Year", ylabel="Nb of Day", clim=(0, 2500)) set_x_yearly(ax, len(births)) show()

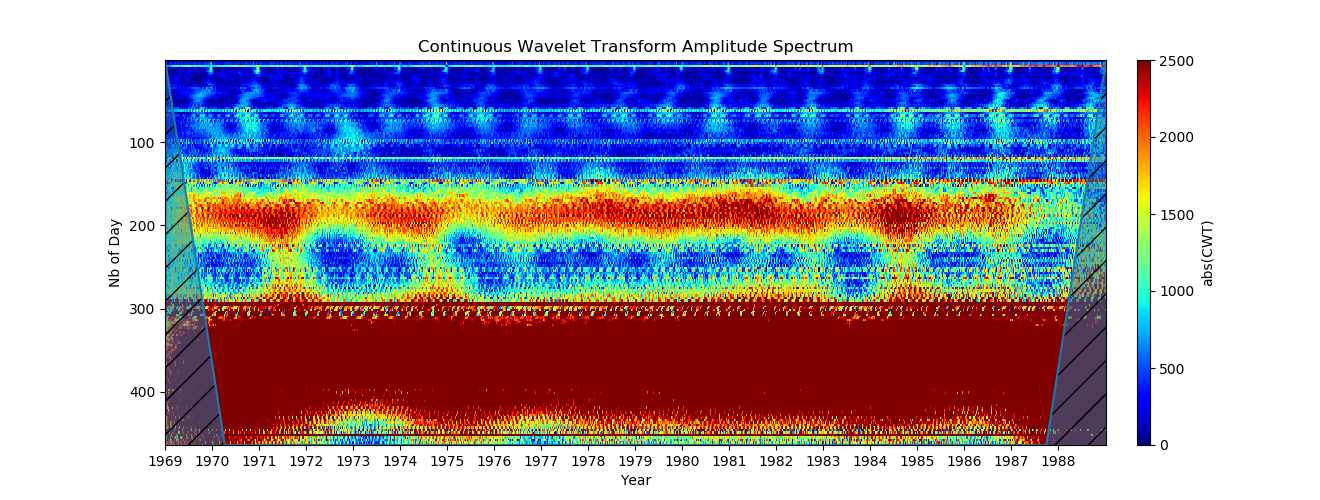
El rango de amplitud del mapa de color (eje Y) ahora se establece mediante clim = (0.2500). El valor exacto de la amplitud de oscilación depende de la wavelet, pero permanecerá cerca del orden del valor real. Esto es mucho mejor, ahora vemos muy bien la variación anual, ¡así como alrededor de 6 meses!

4. Uso de la escala logarítmica (para poder ver períodos pequeños y grandes al mismo tiempo, es mejor usar la escala logarítmica en el eje Y. Esto se logra usando la opción xscale = log).

Listado

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) print("Number of available days:", len(births_normed)) show()

El resultado es mucho mejor, pero ahora los píxeles en valores bajos de períodos se alargan a lo largo del eje Y.

5. Distribución uniforme en una escala logarítmica (para obtener una distribución uniforme en una escala, los valores del período deben distribuirse uniformemente y luego convertirse a valores de escala, como se muestra a continuación :):

Listado

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #  CWT  ,       cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bboxf = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowpropsf = dict(facecolor='yellow', shrink=0.05) text = ax.annotate("unusual\nfeature", xy=(365*6, 15), xytext=(365*3, 50), bbox=bboxf, arrowprops=arrowpropsf) show()

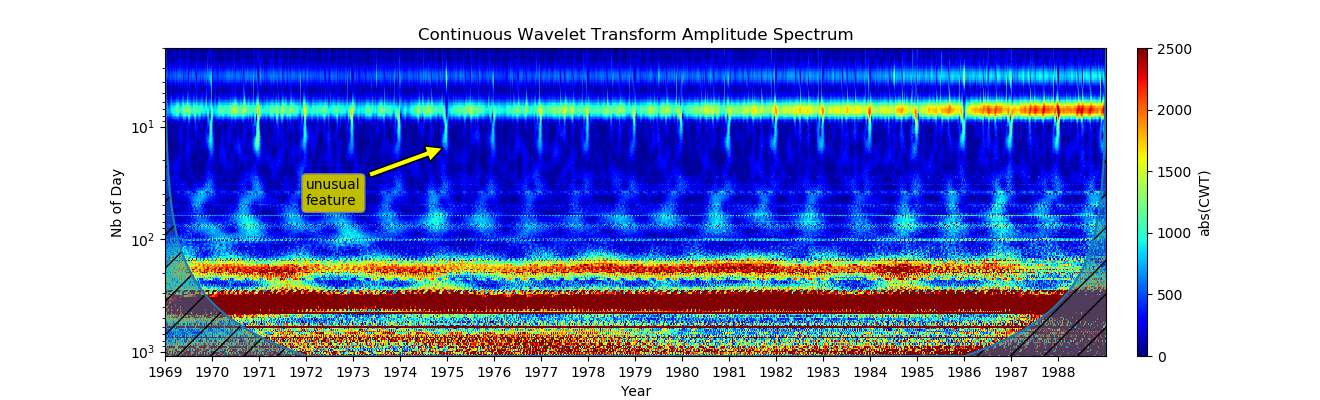
Podemos ver cambios de señal en todas las escalas. El sialograma muestra cada año en períodos iguales.

6. Resaltando parte de la línea de tiempo (Comprobación de datos intermedios entre las marcas de la línea de tiempo en busca de artefactos o datos faltantes):

Listado

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) #    : 1974-1976 fig = figure(figsize=(12,4)) lines =plot(births.index, births.values/1000, '-') xlim(pd.to_datetime("1974-01-01"), pd.to_datetime("1976-01-01")) ylabel("Nb of birthes [k]"); title("Total births per day bw 1974 and 1976"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1974-1969)*365, (1976-1969)*365 ) show()

, , - , :

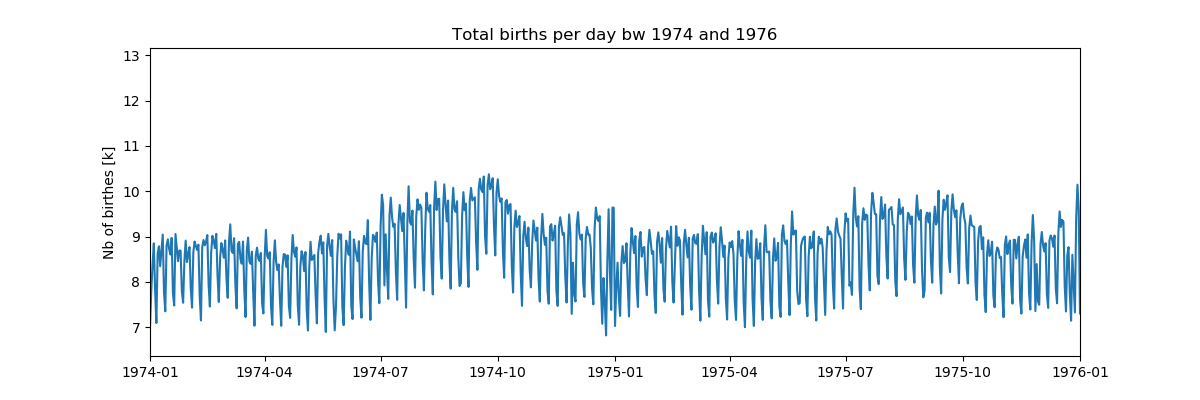
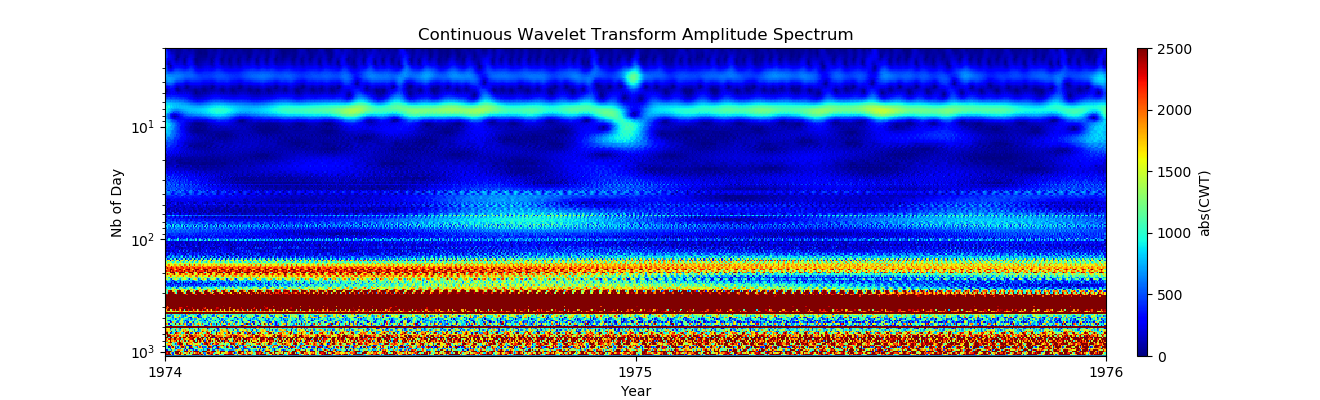
 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) # :  1975    1976  fig = figure(figsize=(12,4)) lines = plot(births.index, births.values/1000, '.-') xlim(pd.to_datetime("1974-12-01"), pd.to_datetime("1975-02-01")) ylabel("Nb of birthes [k]"); title("Total births per day : 2 monthes zoom"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1975-1969)*365-30, (1975-1969)*365+30 ) show()

, :

: 23/24/25 , ;
, 1- 2- ,

7. ( , ):

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bbox = dict(boxstyle="round", facecolor="w", edgecolor="0.5") bbox2 = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowprops = dict(facecolor='white', shrink=0.05) arrowprops2 = dict(facecolor='yellow', shrink=0.05) for period, label in [ (3.5, "half a week"), (7, "one week"), (365/2, "half a year"), (365, "one year"), (365*2.8, "long trends")]: text = ax.annotate(label, xy=(365*5.5, period), xytext=(365*2, period), bbox=bbox, arrowprops=arrowprops) text = ax.annotate("end of year\neffect", xy=(365*6, 15), xytext=(365*3, 50), bbox=bbox2, arrowprops=arrowprops2) text = ax.annotate("increase in\nvariations *amplitude*", xy=(365*18.5, 7), xytext=(365*14, 50), bbox=bbox2, arrowprops=arrowprops2) show()

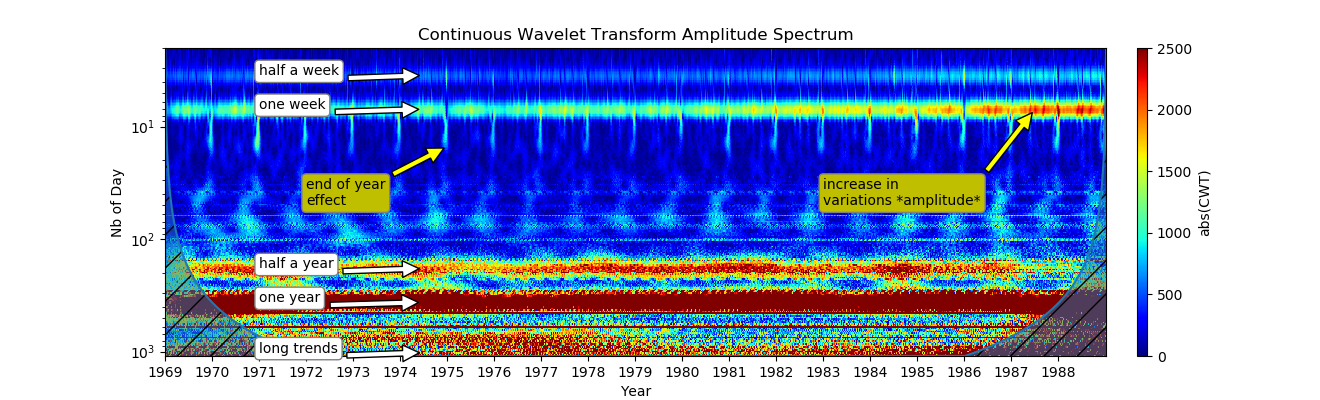
CWT :

, , ;

80- , , ;

— . 3 1 , , . ;

1 . , , .

:

, . , , CWT .

. CWT — , .

, , . – , , mexh gaus5. 1 :

PS :

 >>> import scaleogram; print(scaleogram .__version__) 0.9.5 >>> import pandas; print(pandas .__version__) 0.24.1 >>> import numpy; print(numpy .__version__) 1.16.1 >>> import matplotlib; print(matplotlib .__version__) 3.0.2

*.csv ( ):
year,month,day,gender,births
1969,1,1,F,4046
1969,1,1,M,4440
1969,1,2,F,4454
1969,1,2,M,4548
...
0.24.1 pandas matplotlib.

:

 from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()

Análisis de wavelet. Parte 3

Introduccion

Wavelet - Escalogramas de señal simple

Escalogramas Wavelet de Señales Especiales

Escalogramas de línea de tiempo de wavelet

:

More articles: