ARA: algoritmo para encontrar el número máximo de puntos en una línea recta

Recientemente, me encontré con un problema clásico para las entrevistas: buscar el número máximo de puntos en una línea recta (en un plano, coordenadas enteras). La idea de una búsqueda exhaustiva se me ocurrió de inmediato, lo que tiene una complejidad de tiempo obvia en O (n ^ 2), pero me pareció que debería haber algo más, al menos alguna alternativa en O (n * log (n)) . Después de media hora, ¡incluso se encontró algo mejor!



_{Una declaración más detallada del problema con ejemplos de entrada-salida está en GeeksForGeeks y LeetCode}

Al principio noté que puede resolver fácilmente el problema solo para líneas horizontales o verticales, agregando la X / Y de cada punto en el diccionario. ¿Y cuál es la diferencia entre las otras líneas? ¿Solo una pendiente? ... ¡Pero es reparable!

Por lo tanto, decidí que era posible recorrer la lista completa de puntos varias veces rotándolos. ¡Y se obtiene la solución en O (n)! Aunque con un gran coeficiente. Realmente espero no haber inventado una bicicleta :)

# ***  *** #   #    = 180/ROT_COUNT  # #      12, #  180*4    (6% ), #  180*20   (0% ). # ó    . #     - . ROT_COUNT = 180*10 #  #        , #       1 / MULT_COEF. #    4  . #   MULT_COEF   ROT_COUNT. # ó    - . #     - . MULT_COEF = 2 ** 3 angles = list(map(lambda x: x*180.0/ROT_COUNT, range(ROT_COUNT))) def mnp_rotated(points, angle): """Returns Maximum Number of Points on the same line with given rotation""" #   rad = math.radians(angle) co = math.cos(rad) si = math.sin(rad) #      counts = {} for pair in points: #    nx = pair[0]*co - pair[1]*si #       , #      #       #      nx = int(nx * MULT_COEF) #   if nx in counts: counts[nx] += 1 else: counts[nx] = 1 #    return max(counts.values()) def mnp(points): """Returns Maximum Number of Points on the same line""" res = 0 best_angle = 0 #      for i in angles: current = mnp_rotated(points, i) #  ,     if current > res: res = current best_angle = i return res 

Visualizado, se ve más o menos así:
_{mi primer GIF casero, no me regañes :)}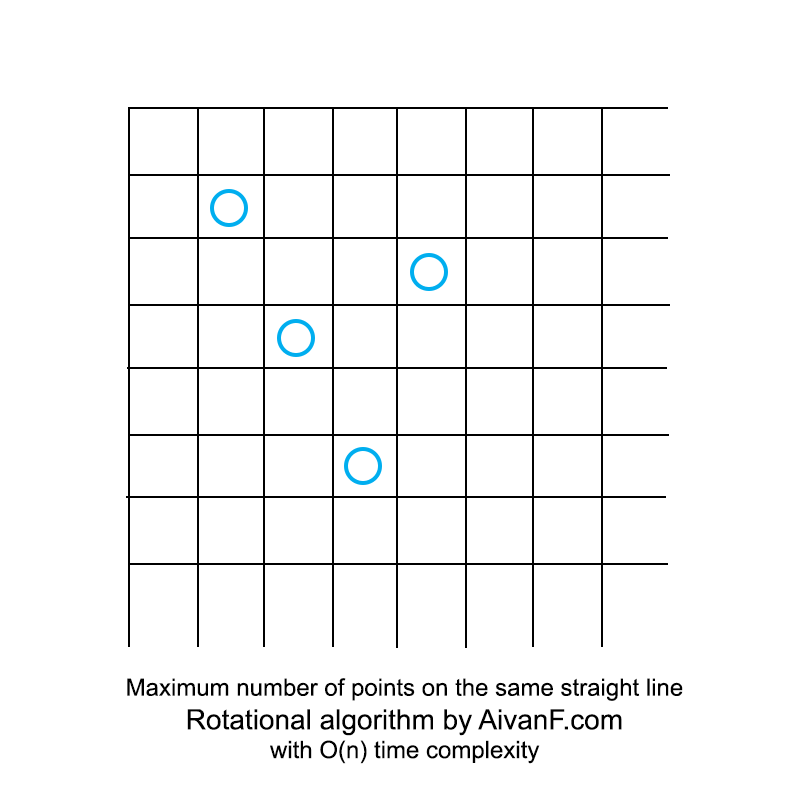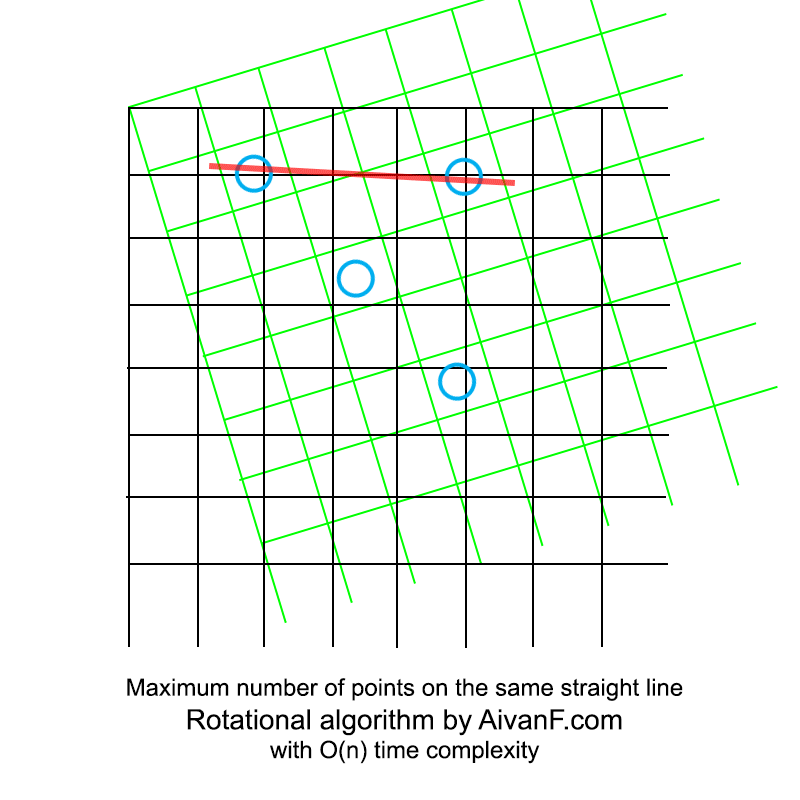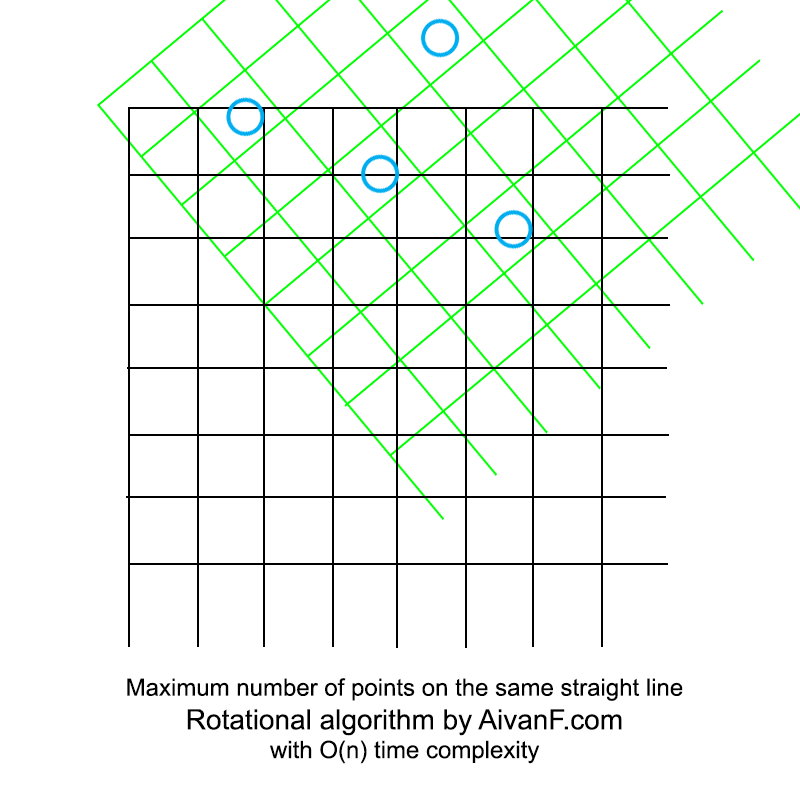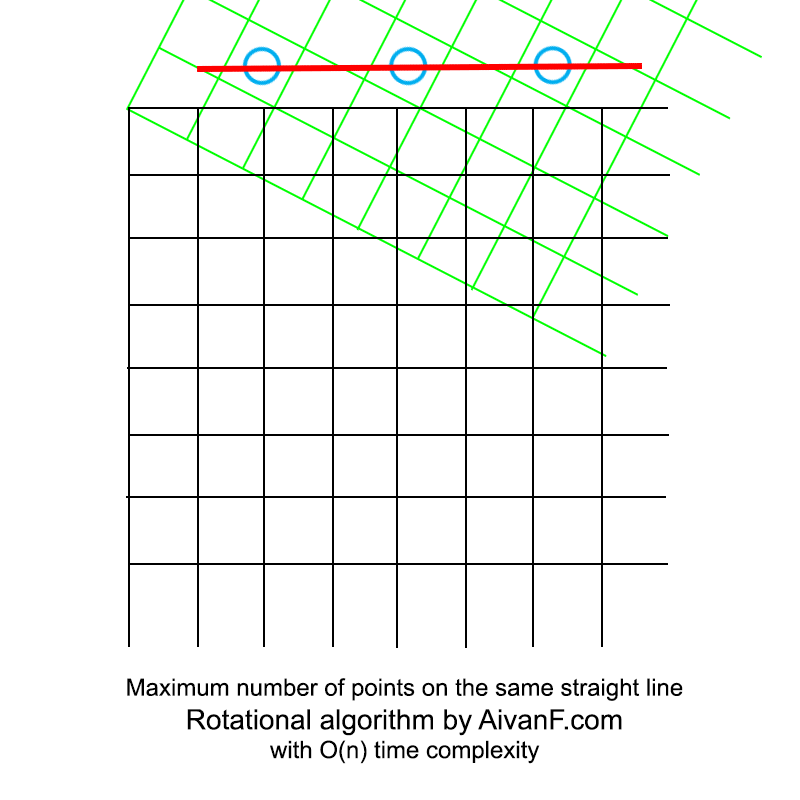



Es interesante observar que la implementación posterior de una búsqueda exhaustiva tomó más líneas de código.

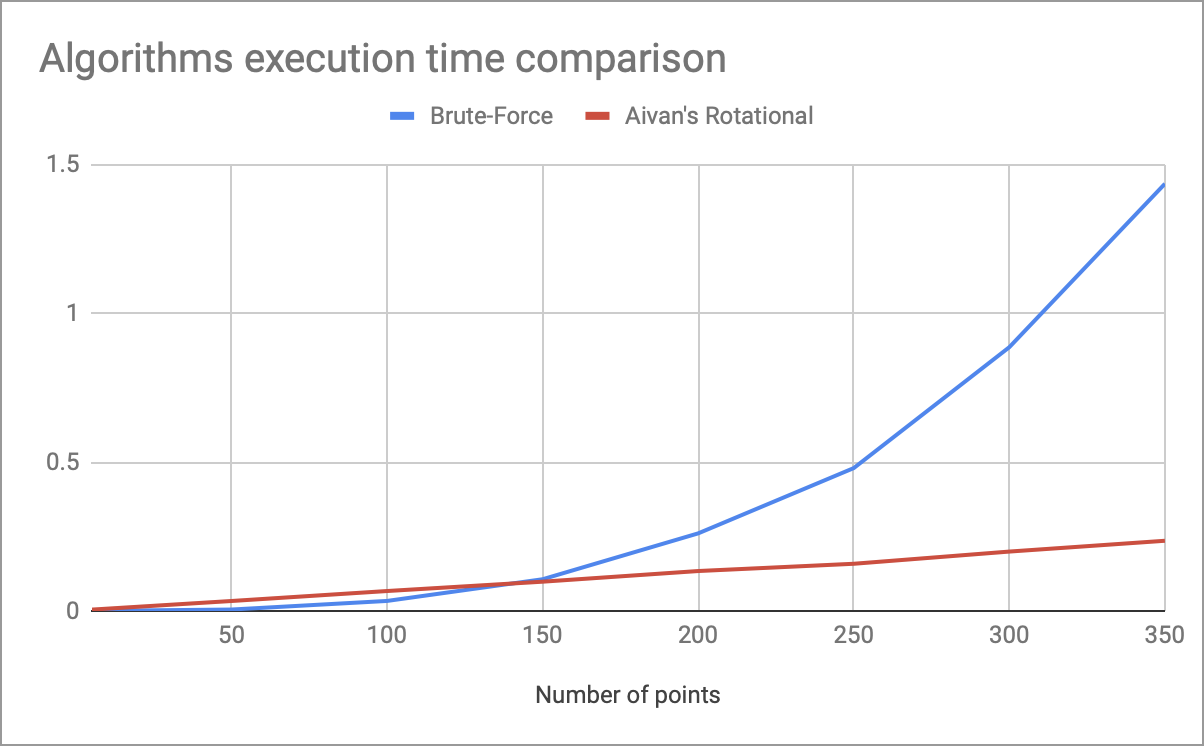
El gráfico con las mediciones del tiempo de ejecución de mi algoritmo de rotación y la enumeración completa según el número de puntos se encuentra en el encabezado.


Aproximadamente 150 puntos muestran la ventaja de la complejidad lineal en el tiempo (con los coeficientes utilizados en el código anterior). Como resultado, este algoritmo tiene las siguientes desventajas:

• La precisión no es absoluta.
• El tiempo de ejecución en pequeños conjuntos de puntos es largo.
  _{En general, esto se corrige fácilmente mediante una selección competente de coeficientes: para conjuntos simples, ROT_COUNT = 36 en lugar de 2000 es suficiente, lo que acelera el código más de 50 veces.}

Y tales ventajas:

• Funciona con calma con coordenadas fraccionarias.
• La complejidad temporal es lineal, lo que se nota en grandes conjuntos de datos.

Una tabla con medidas está disponible aquí . El código fuente completo del proyecto con ambos algoritmos y varias comprobaciones está en GitHub .

Actualización Quiero señalar una vez más que este algoritmo tiene ventajas y desventajas, no lo defiendo como un reemplazo ideal para la fuerza bruta, acabo de describir una posible alternativa interesante, que en algunos casos puede ser más apropiada.