Bandas de bits de hardware CortexM3 / M4 (ARM), arquitectura de kernel, ensamblador, C / C ++ 14 y una gota de metaprogramación

Introduccion

Atención, este no es otro artículo de "Hola mundo" sobre cómo parpadear un LED o entrar en su primera interrupción en STM32. Sin embargo, traté de dar explicaciones completas sobre todos los problemas planteados, por lo que el artículo será útil no solo para muchos profesionales y soñando con convertirse en tales desarrolladores (como espero), sino también para programadores novatos de microcontroladores, ya que este tema, por alguna razón, circula en innumerables sitios / blogs "profesores de programación MK".

¿Por qué decidí escribir esto?

Aunque exageré, habiendo dicho antes que la banda de bits de hardware de la familia Cortex-M no se describe en recursos especializados, todavía hay lugares donde se cubre esta característica (e incluso conocí un artículo aquí), pero este tema claramente necesita ser complementado y modernizado. Observo que esto también se aplica a los recursos en inglés. En la siguiente sección, explicaré por qué esta característica del núcleo puede ser extremadamente importante.

Teoría

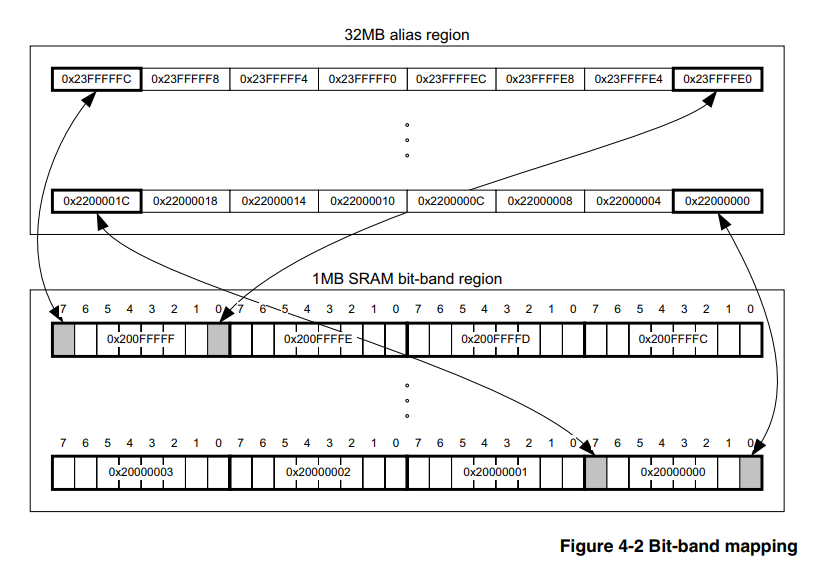
(y aquellos que la conocen pueden comenzar a practicar de inmediato)
Las bandas de bits de hardware son una característica del núcleo en sí y, por lo tanto, no dependen de la familia y la compañía del fabricante de microcontroladores, lo principal es que el núcleo es adecuado. En nuestro caso, que sea Cortex-M3. Por lo tanto, la información sobre este tema debe buscarse en un documento oficial sobre el núcleo mismo, y existe dicho documento, aquí está , la sección 4.2 describe en detalle cómo usar esta herramienta.

Aquí me gustaría hacer una pequeña digresión técnica para los programadores que no están familiarizados con el ensamblador, de los cuales la mayoría lo están ahora, debido a la complejidad propagandizada y la inutilidad del ensamblador para microcontroladores "serios" de 32 bits como STM32, LPC, etc. Además, a menudo se pueden encontrar intentos censura por el uso de ensamblador en esta área, incluso en el Habr. En esta sección, quiero describir brevemente el mecanismo de escritura en la memoria MK, que debería aclarar las ventajas de las bandas de bits.

Explicaré un ejemplo simple específico para la mayoría de STM32. Supongamos que necesito convertir PB0 en una salida de uso general. Una solución típica se vería así:

GPIOB->MODER |= GPIO_MODER_MODER0_0; 

Obviamente, usamos el "OR" bit a bit para no sobrescribir los bits restantes del registro.

Para el compilador, esto se traduce en el siguiente conjunto de 4 instrucciones:

1. Descargue GPIOB-> MODER al registro de propósito general (RON)
2. Cargue los valores al otro RON en la dirección indicada en el RON de p1.
3. Haga un OR bit a bit de este valor con GPIO_MODER_MODER0_0.
4. Descargue el resultado de nuevo a GPIOB-> MODER.

Además, no se debe olvidar que este núcleo utiliza el conjunto de instrucciones thumb2, lo que significa que pueden ser diferentes en volumen. También noto que en todas partes estamos hablando del nivel de optimización O3.

En lenguaje ensamblador, se ve así:



Se puede ver que la primera instrucción no es más que una seudoinstrucción con un desplazamiento, encontramos la dirección del registro en la dirección de la PC (dada la cinta transportadora) + 0x58.



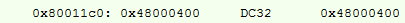
Resulta que tenemos 4 pasos (y más ciclos de reloj) y 14 bytes de memoria ocupada por operación.
Si quieres saber más sobre esto, te recomiendo el libro [2], por cierto, también está en ruso.

Pasamos al método bit_banding.

La esencia, según el campesino, es que el procesador tiene un área de memoria especialmente asignada, escribiendo los valores en los que no cambiamos otros bits del registro periférico o RAM. Es decir, no necesitamos cumplir con los puntos 2) y 3) descritos anteriormente, y para esto es suficiente contar la dirección de acuerdo con las fórmulas de [1].



Estamos tratando de hacer una operación similar, su ensamblador:



Dirección recalculada:



Aquí agregamos una instrucción de escritura # 1 en el RON, pero de todos modos, el resultado es 10 bytes, en lugar de 14, y un par de ciclos de reloj menos.

Pero, ¿y si la diferencia es ridícula?

Por un lado, los ahorros no son significativos, especialmente en ciclos cuando ya es un hábito hacer overclocking del controlador a 168 MHz. En un proyecto promedio, los momentos en los que puede aplicar este método serán de 40 a 80, respectivamente, en bytes, el ahorro puede alcanzar los 250 bytes si las direcciones difieren. Y si consideramos que programar MK directamente en los registros ahora se considera "zashkvar", y es "genial" usar todo tipo de cubos de dados, entonces los ahorros pueden ser mucho más.

Además, la cifra de 250 bytes está distorsionada por el hecho de que las bibliotecas de alto nivel se usan activamente en la comunidad, el firmware se infla a tamaños indecentes. Cuando se programa a un nivel bajo, esto es al menos del 2 al 5% del volumen del software para un proyecto promedio, con arquitectura competente y optimización de O3.

Nuevamente, no quiero decir que esta es una especie de herramienta super-duper-mega cool que todo programador de MK que se precie debería usar. Pero si puedo reducir los costos incluso en una parte tan pequeña, ¿por qué no?

Implementación

Todas las opciones se darán solo para configurar los periféricos, ya que no encontré una situación en la que fuera necesario para la RAM. Estrictamente hablando, para RAM, la fórmula es similar, solo cambie las direcciones base para el cálculo. Entonces, ¿cómo implementas esto?

Ensamblador

Vayamos desde abajo, desde mi amado Ensamblador.

En los proyectos de ensamblador, generalmente asigno un par de RON de 2 bytes (de acuerdo con las instrucciones que funcionan con ellos) bajo # 0 y # 1 para todo el proyecto, y los uso también en macros, lo que me reduce otros 2 bytes de forma continua. Observación, no encontré CMSIS en Assembler para STM, porque puse el número de bit en la macro de inmediato, y no su valor de registro.


Ejemplos:


La ventaja indudable de esta opción es que tenemos control total, lo que no se puede decir sobre otras opciones. Y como lo mostrará la última sección del artículo, además esta es muy significativa.

Sin embargo, nadie necesita proyectos para MK en Assembler, desde aproximadamente el final del cero, lo que significa que debe cambiar a SI.

Llanura c

Honestamente, encontré una opción simple de Sishny al comienzo del camino, en algún lugar de la vasta red. En ese momento, ya implementé las bandas de bits en Assembler, y accidentalmente tropecé con un archivo C, funcionó de inmediato y decidí no inventar nada.


Como puede ver, un código muy simple y directo escrito en el lenguaje del procesador. El trabajo principal aquí es la traducción de los valores de CMSIS a un número de bit, que estaba ausente como una necesidad de una versión de ensamblador.

Oh sí, usa esta opción así:


Sin embargo, las tendencias modernas (masivamente, según mis observaciones, aproximadamente a partir de 2015) están a favor de reemplazar C con C ++ incluso para MK. Y las macros no son la herramienta más confiable, por lo que la próxima versión estaba destinada a nacer.

Cpp03

Aquí, una herramienta muy interesante y discutida, pero poco utilizada en vista de su complejidad, con un ejemplo trillado de factorial, la herramienta es la metaprogramación.

Después de todo, la tarea de traducir el valor de una variable a un número de bit es ideal (ya hay valores en CMSIS), y en este caso es práctico para el tiempo de compilación.

Implementé esto de la siguiente manera usando plantillas:


Puedes usarlo de la misma manera:


¿Y por qué quedó la macro? El hecho es que no conozco otra forma de insertar esta operación sin tener que ir a otra área del código del programa. Me alegraría mucho si me incitaran en los comentarios. Ni las plantillas ni las funciones en línea ofrecen tal garantía. Sí, y la macro aquí hace frente a su tarea perfectamente bien, no tiene sentido cambiarla solo porque el conformista alguien considera que esto "no es seguro".

Sorprendentemente, el tiempo aún no se detuvo, los compiladores admitieron cada vez más C ++ 14 / C ++ 17, por qué no aprovechar las innovaciones, haciendo que el código sea más comprensible.

Cpp14 / cpp17

Como puede ver, acabo de reemplazar las plantillas con una función constexpr recursiva, que, en mi opinión, es más clara para el ojo humano.

Use de la misma manera. Por cierto, en C ++ 17, en principio, puede usar la función recursiva lambda constexpr, pero no estoy seguro de que esto conduzca al menos a algunas simplificaciones, y tampoco complicará el orden del ensamblador.

En resumen, las tres implementaciones de C / Cpp proporcionan un conjunto igualmente correcto de instrucciones, de acuerdo con la sección Teoría. He estado trabajando con todas las implementaciones en IAR ARM 8.30 y gcc 7.2.0 durante mucho tiempo.

La practica es una perra

Eso es todo, al parecer, sucedió. Se calcularon los ahorros de memoria, se eligió la implementación, listos para mejorar el rendimiento. No aquí, fue solo un caso de una divergencia de teoría y práctica. ¿Y cuándo fue diferente?

Nunca lo habría publicado si no lo hubiera probado, pero cuánto se reduce de manera realista el volumen ocupado en los proyectos. Específicamente, en un par de proyectos antiguos, reemplacé esta macro con una implementación regular sin máscara, y miré la diferencia. El resultado sorprendió desagradablemente.

Al final resultó que, el volumen permanece prácticamente sin cambios. Elegí específicamente proyectos donde se usaban exactamente 40-50 de tales instrucciones. Según la teoría, tenía que guardar bien al menos 100 bytes, y como máximo 200. En la práctica, la diferencia resultó ser de 24 a 32 bytes. Pero por que?

Por lo general, cuando configura periféricos, configura 5-10 registros casi seguidos. Y a un alto nivel de optimización, el compilador no organiza las instrucciones exactamente en el orden de los registros, sino que las organiza como parece correcto, interfiriendo a veces en lugares aparentemente inextricables.

Veo dos opciones (aquí están mis especulaciones):

1. O el compilador es tan inteligente que sabe por usted cómo será mejor optimizar el conjunto de instrucciones
2. O el compilador aún no es más inteligente que una persona, y se confunde a sí mismo cuando se encuentra con tales construcciones.

Es decir, resulta que este método en lenguajes de "alto nivel" con un alto nivel de optimización solo funciona correctamente si no hay operaciones similares cerca de una de esas operaciones.

Por cierto, en el nivel O0, la teoría y la práctica convergen en cualquier caso, pero este nivel de optimización no me interesa.

Resumo

Un resultado negativo también es un resultado. Creo que todos sacarán conclusiones por sí mismos. Personalmente, continuaré usando esta técnica, ciertamente no será peor.

Espero que haya sido interesante y quiero expresar un gran respeto a aquellos que han leído hasta el final.

Lista de literatura

1. "Manual de referencia técnica de Cortex-M3", Sección 4.2, ARM 2005.
2. La guía definitiva para el ARM Cortex-M3, Joseph Yiu.

PD: Tengo en mi cartera una pequeña cobertura de temas relacionados con el desarrollo de la electrónica integrada. Avíseme, si está interesado, los recibiré lentamente.

PPS De alguna manera resultó torcido insertar secciones del código, por favor dígame cómo mejorar, si es posible. En general, puede copiar un código de interés en el bloc de notas y evitar emociones desagradables en el análisis.

UPD:

A petición de los lectores, indico que la operación de banda de bits en sí misma es atómica, lo que nos da cierta seguridad al trabajar con registros. Esta es una de las características más importantes de este método.