
Cómo hacer un solucionador de nonogramas para Python, vuelva a escribirlo en Rust para ejecutarlo directamente en el navegador a través de WebAssembly.
TL; DR
Inicio
Sobre los crucigramas japoneses (nonogramas) en el Habré ya había varias publicaciones. Ejemplo
y uno mas
Las imágenes se cifran con números ubicados a la izquierda de las filas, así como arriba de las columnas. El número de números muestra cuántos grupos de celdas negras (o su color, para crucigramas de color) hay en la fila o columna correspondiente, y los números mismos: cuántas celdas combinadas contiene cada uno de estos grupos (por ejemplo, un conjunto de tres números: 4, 1 y 3 significa que en esta fila hay tres grupos: el primero, de cuatro, el segundo, de uno, el tercero, de tres celdas negras). En un crucigrama en blanco y negro, los grupos deben estar separados por al menos una celda vacía; en el crucigrama de color, esta regla se aplica solo a grupos de un color, y los grupos de varios colores pueden estar muy separados (las celdas vacías también pueden estar a lo largo de los bordes de las filas). Es necesario determinar la ubicación de los grupos celulares.
Uno de los puntos de vista más generalmente aceptados es que los crucigramas "correctos" solo pueden llamarse aquellos que se resuelven de manera "lógica". Esto generalmente se llama el método de solución, en el que las dependencias entre diferentes filas y / o columnas no se tienen en cuenta. En otras palabras, una solución es una secuencia de decisiones independientes de filas o columnas individuales hasta que se llenen todas las celdas (más sobre el algoritmo a continuación). Por ejemplo, solo dichos nonogramas se pueden encontrar en el sitio web http://nonograms.org/ ( http://nonograms.ru/ ). Los nonogramas de este sitio ya se han citado como ejemplo en el artículo Resolver crucigramas japoneses a la velocidad de la luz . Para fines de comparación y verificación, mi solucionador también agregó soporte para descargar y analizar crucigramas de este sitio (gracias a KyberPrizrak por el permiso para usar materiales de su sitio).
Sin embargo, el concepto de nonogramas puede extenderse a un problema más general, cuando el método "lógico" habitual conduce a un callejón sin salida. En tales casos, uno debe hacer una suposición sobre el color de una celda y, después de probar que este color conduce a una contradicción, marcar el color opuesto para esta celda. La secuencia de tales pasos puede (si tiene paciencia) darnos todas las soluciones. Este artículo tratará principalmente de resolver un caso tan general de crucigramas.
Pitón
Hace aproximadamente un año y medio, accidentalmente me topé con un artículo que describía un método para resolver una sola línea (como resultó más tarde, el método fue bastante lento).
Cuando implementé este método en Python (mi lenguaje de trabajo principal) y agregué una actualización secuencial de todas las líneas, vi que todo esto no se estaba resolviendo muy rápidamente. Después de estudiar el material, resultó que en este tema hay muchos trabajos e implementaciones que ofrecen diferentes enfoques para esta tarea.
Me pareció que el trabajo más ambicioso sobre el análisis de varias implementaciones de solucionador fue realizado por Jan Wolter, que publicó en su sitio (que, hasta donde yo sé, sigue siendo el mayor repositorio público de nonogramas en Internet), un estudio detallado que contiene una gran cantidad de información y enlaces que pueden ayudar en creando tu propio solucionador.
Al estudiar numerosas fuentes (estarán al final del artículo), gradualmente mejoré la velocidad y la funcionalidad de mi solucionador. Como resultado, era adicto y estaba involucrado en la implementación, refactorización y depuración de algoritmos durante aproximadamente 10 meses en un tiempo libre del trabajo.
Algoritmos centrales
El solucionador resultante se puede representar en forma de cuatro niveles de decisión:
( línea ) solucionador lineal: en la entrada, una línea de celdas y una línea descriptiva (pistas), en la salida, una línea parcialmente resuelta. En la solución de Python, implementé 4 algoritmos diferentes (3 de ellos están adaptados para crucigramas en color). El más rápido resultó ser el algoritmo BguSolver, llamado así por la fuente original . Este es un método muy efectivo y prácticamente estándar para resolver cadenas de nonogramas utilizando programación dinámica. El pseudocódigo de este método se puede encontrar, por ejemplo, en este artículo .
( propagación ) colocamos todas las filas y columnas en una cola, la revisamos con un solucionador lineal, cuando recibimos nueva información al resolver una fila (columna), actualizamos la cola, respectivamente, con nuevas columnas (filas). Continúe hasta que la línea esté vacía.
Ejemplo y códigoTomamos la siguiente tarea para resolver desde la cola. Sea una cadena vacía (no resuelta) de longitud 7 (la denotamos como ??????? ) con una descripción de los bloques [2, 3] . El solucionador lineal producirá una cadena parcialmente resuelta ?X??XX? donde X es la celda llena. Al actualizar la fila, vemos que las columnas con los números 1, 4, 5 han cambiado (la indexación comienza en 0). Esto significa que ha aparecido nueva información en las columnas indicadas y que pueden devolverse al solucionador "lineal". Ponemos estas columnas en la cola de tareas con mayor prioridad (para luego darlas al solucionador lineal).
def propagation(board): line_jobs = PriorityDict() for row_index in range(board.height): new_job = (False, row_index) line_jobs[new_job] = 0 for column_index in range(board.width): new_job = (True, column_index) line_jobs[new_job] = 0 for (is_column, index), priority in line_jobs.sorted_iter(): new_jobs = solve_and_update(board, index, is_column) for new_job in new_jobs:
( sondeo ) para cada celda no resuelta, clasificamos todas las opciones de color e intentamos la propagación con esta nueva información. Si obtenemos una contradicción, descartamos este color de las opciones de color para la celda e intentamos beneficiarnos nuevamente utilizando la propagación. Si se resuelve hasta el final, agregamos la solución a la lista de soluciones, pero continuamos experimentando con otros colores (puede haber varias soluciones). Si llegamos a una situación en la que es imposible resolverlo más, simplemente ignoramos y repetimos el procedimiento con un color / celda diferente.
CódigoDevuelve True si se recibe una contradicción como resultado de la muestra.
def probe(self, cell_state): board = self.board pos, assumption = cell_state.position, cell_state.color
( retroceso ) si durante el sondeo no ignora un rompecabezas parcialmente resuelto, pero continúa invocando recursivamente el mismo procedimiento, obtenemos un retroceso (en otras palabras, una caminata completa en la profundidad del árbol de decisión potencial). Aquí, comienza a jugar un papel importante, cuál de las células se elegirá como la próxima extensión de la solución potencial. Buena investigación sobre este tema se encuentra en esta publicación .
CódigoRetroceder es bastante complicado conmigo, pero estas dos funciones describen aproximadamente lo que sucede durante una búsqueda recursiva
def search(self, search_directions, path=()): """ Return False if the given path is a dead end (no solutions can be found) """ board = self.board depth = len(path) save = board.make_snapshot() try: while search_directions: state = search_directions.popleft() assumption, pos = state.color, state.position cell_colors = board.cell_colors(pos) if assumption not in cell_colors: LOG.warning("The assumption '%s' is already expired. " "Possible colors for %s are %s", assumption, pos, cell_colors) continue if len(cell_colors) == 1: LOG.warning('Only one color for cell %r left: %s. Solve it unconditionally', pos, assumption) try: self._solve_without_search() except NonogramError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The path %s is invalid", assumption, pos, path) return False if board.is_solved_full: self._add_solution() LOG.warning( "The only color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True continue rate = board.solution_rate guess_save = board.make_snapshot() try: LOG.warning('Trying state: %s (depth=%d, rate=%.4f, previous=%s)', state, depth, rate, path) success = self._try_state(state, path) finally: board.restore(guess_save) if not success: try: LOG.warning( "Unset the color %s for cell '%s'. Solve it unconditionally", assumption, pos) board.unset_color(state) self._solve_without_search() except ValueError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The whole branch (depth=%d) is invalid. ", assumption, pos, depth) return False if board.is_solved_full: self._add_solution() LOG.warning( "The negation of color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True finally:
Entonces, comenzamos a resolver nuestro crucigrama desde el segundo nivel (el primero solo es adecuado para el caso degenerado, cuando en todo el crucigrama solo hay una fila o columna) y gradualmente subimos los niveles. Como puede suponer, cada nivel causa el nivel subyacente varias veces, por lo que para una solución efectiva es imperativo tener un primer y segundo nivel rápidos, que se pueden invocar millones de veces para acertijos complejos.
En esta etapa, resulta (bastante esperado) que Python no es la herramienta adecuada para el máximo rendimiento en una tarea tan intensiva de CPU: todos los cálculos son extremadamente ineficientes en comparación con los lenguajes de nivel inferior. Por ejemplo, el solucionador BGU más cerrado algorítmicamente (en Java), según los resultados de las mediciones, resultó ser 7-17 (a veces hasta 27) veces más rápido en una variedad de tareas.
Más detalles pynogram_my BGU_my speedup
Bailarina 0.976 0.141 6.921986
Gato 1.064 0.110 9.672727
Patín 1.084 0.101 10.732673
Dólares 1.116 0.118 9.457627
Borde 1.208 0.094 12.851064
Humo 1.464 0.120 12.200000
Nudo 1.332 0.140 9.514286
Swing 1.784 0.138 12.927536
Mamá 2.108 0.147 14.340136
DiCap 2.076 0.176 11.795455
Trágico 2.368 0.265 8.935849
Merka 2.084 0.196 10.632653
Petro 2.948 0.219 13.461187
M&M 3.588 0.375 9.568000
Firmado 4.068 0.242 16.809917
Luz 3.848 0.488 7.885246
Por siempre 111.000 13.570 8.179808
Centro 5.700 0.327 17.431193
Caliente 3.150 0.278 11.330935
Karate 2.500 0.219 11.415525
9-Dom 510.000 70.416 7.242672
Bandera 149.000 5.628 26.474769
León 71.000 2.895 24.525043
Marley 12.108 4.405 2.748695
Cosa 321.000 46.166 6.953169
Nature inf 433.138 inf
Sierp inf inf NaN
Gettys inf inf NaN
Las mediciones se realizaron en mi automóvil, los rompecabezas se toman del conjunto estándar que Jan Wolter usó en su comparación
¡Y esto ya es después de que comencé a usar PyPy, y en CPython estándar el tiempo de cálculo fue más largo que en PyPy 4-5 veces! Podemos decir que el rendimiento de un solucionador de Java similar resultó ser 28-85 veces mayor que el código CPython.
Los intentos de mejorar el rendimiento de mi solucionador mediante la creación de perfiles (cProfile, SnakeViz, line_profiler) condujeron a cierta aceleración, pero, por supuesto, no dieron un resultado sorprendente.
+ solucionador puede resolver todos los rompecabezas de los sitios https://webpbn.com , http://nonograms.org y su propio formato (basado en ini)
+ resuelve nonogramas en blanco y negro y en color con cualquier número de colores (el número máximo de colores que se reunieron es 10)
+ resuelve acertijos con bloques faltantes (borrados). Un ejemplo de tal rompecabezas .
+ puede hacer rompecabezas a la consola / a las maldiciones / ventana en el navegador (al instalar la opción web-pynogram adicional). Para todos los modos, se admite la visualización del progreso de la solución en tiempo real.
- cálculos lentos (en comparación con las implementaciones descritas en la comparación de artículos de solucionadores, ver tabla ).
- retroceso ineficiente: algunos acertijos se pueden resolver durante horas (cuando el árbol de decisión es muy grande).
Herrumbre
A principios de año, comencé a estudiar Rust. Comencé, como siempre, con The Book , aprendí sobre WASM, revisé el tutorial propuesto . Sin embargo, quería una tarea real en la que pueda participar en las fortalezas del lenguaje (principalmente su súper rendimiento), y no algunos ejemplos inventados por alguien. Entonces volví a los nonogramas. Pero ahora ya tenía una versión funcional de todos los algoritmos en Python, se dejó "reescribir".
La buena noticia me esperaba desde el principio: resultó que Rust, con su sistema de tipos, describe perfectamente las estructuras de datos para mi tarea. Por ejemplo, una de las correspondencias básicas BinaryColor + BinaryBlock / MultiColor + ColoredBlock le permite separar permanentemente nonogramas en blanco y negro y en color. Si en algún lugar del código tratamos de resolver una cadena de color utilizando bloques de descripción binaria ordinarios, obtenemos un error de compilación sobre la falta de coincidencia de tipos.
Los tipos básicos se parecen a esto pub trait Color { fn blank() -> Self; fn is_solved(&self) -> bool; fn solution_rate(&self) -> f64; fn is_updated_with(&self, new: &Self) -> Result<bool, String>; fn variants(&self) -> Vec<Self>; fn as_color_id(&self) -> Option<ColorId>; fn from_color_ids(ids: &[ColorId]) -> Self; } pub trait Block { type Color: Color; fn from_str_and_color(s: &str, color: Option<ColorId>) -> Self { let size = s.parse::<usize>().expect("Non-integer block size given"); Self::from_size_and_color(size, color) } fn from_size_and_color(size: usize, color: Option<ColorId>) -> Self; fn size(&self) -> usize; fn color(&self) -> Self::Color; } #[derive(Debug, PartialEq, Eq, Hash, Clone)] pub struct Description<T: Block> where T: Block, { pub vec: Vec<T>, }
Al portar el código, algunos puntos indican claramente que un lenguaje estáticamente escrito como Rust (bueno, o, por ejemplo, C ++) es más adecuado para esta tarea. Más precisamente, los genéricos y los rasgos describen un dominio mejor que las jerarquías de clase. Entonces, en el código Python, tuve dos clases para un BguSolver lineal, BguSolver y BguColoredSolver que resolvieron una línea en blanco y negro y una línea de color, respectivamente. En el código Rust, todavía tengo la única struct DynamicSolver<B: Block, S = <B as Block>::Color> genérica struct DynamicSolver<B: Block, S = <B as Block>::Color> , que puede resolver ambos tipos de tareas, dependiendo del tipo pasado durante la creación ( DynamicSolver<BinaryBlock>, DynamicSolver<ColoredBlock> ). Esto, por supuesto, no significa que no se pueda hacer algo similar en Python, solo en Rust, el sistema de tipos me indicó claramente que si no seguías este camino, tendrías que escribir una tonelada de código repetido.
Además, cualquiera que haya intentado escribir en Rust, sin duda notó el efecto de "confianza" en el compilador, cuando el proceso de escribir código se reduce al siguiente algoritmo pseudo-meta:
escribir_código_inicial
while (compiler_hints = $ (carga check))! = 0; hacer
fix_errors (compiler_hints)
fin
Cuando el compilador deja de emitir errores y advertencias, su código será coherente con el sistema de tipos y el verificador de préstamos y le avisará con anticipación de un montón de posibles errores (por supuesto, siempre que los tipos de datos estén cuidadosamente diseñados).
Daré un par de ejemplos de funciones que muestran cuán conciso puede ser el código Rust (en comparación con las contrapartes de Python).
unsighved_neighboursDa una lista de "vecinos" no resueltos para un punto dado (x, y)
def unsolved_neighbours(self, position): for pos in self.neighbours(position): if not self.is_cell_solved(*pos): yield pos
fn unsolved_neighbours(&self, point: &Point) -> impl Iterator<Item = Point> + '_ { self.neighbours(&point) .into_iter() .filter(move |n| !self.cell(n).is_solved()) }
sumas parcialesPara un conjunto de bloques que describe una línea, dé sumas parciales (teniendo en cuenta los espacios requeridos entre los bloques). Los índices resultantes indicarán la posición mínima en la que puede terminar el bloque (esta información se usa más adelante para un solucionador lineal).
Por ejemplo, para tal conjunto de bloques [2, 3, 1] tenemos en la salida [2, 6, 8] , lo que significa que el primer bloque se puede desplazar al máximo hacia la izquierda para que su borde derecho ocupe la segunda celda, de manera similar para el resto bloques:
1 2 3 4 5 6 7 8 9
_ _ _ _ _ _ _ _ _ _
2 3 1 | _ | _ | _ | _ | _ | _ | _ | _ | _ |
^ ^ ^
El | El | El |
final de 1 bloque | El | El |
final del bloque 2 -------- |
final del bloque 3 ------------
@expand_generator def partial_sums(blocks): if not blocks: return sum_so_far = blocks[0] yield sum_so_far for block in blocks[1:]: sum_so_far += block + 1 yield sum_so_far
fn partial_sums(desc: &[Self]) -> Vec<usize> { desc.iter() .scan(None, |prev, block| { let current = if let Some(ref prev_size) = prev { prev_size + block.0 + 1 } else { block.0 }; *prev = Some(current); *prev }) .collect() }
Al portar, hice varios cambios
Herramientas utiles
- Clippy es un analizador estático estándar que a veces incluso puede dar consejos que aumentan ligeramente el rendimiento del código.
- valgrind es una herramienta para el análisis dinámico de aplicaciones. Lo utilicé como generador de perfiles para buscar botneks (
valrgind --tool=callgrind ) y particularmente secciones de código con valrgind --tool=massif ( valrgind --tool=massif ). Consejo: establezca [profile.release] debug = true en Cargo.toml antes de iniciar el generador de perfiles. Esto dejará caracteres de depuración en el ejecutable. - kcachegrind para ver archivos callgrind. Una herramienta muy útil para encontrar los lugares más problemáticos en términos de rendimiento.
Rendimiento
Eso por lo que se inició la reescritura en Rust. Tomamos los crucigramas de la tabla de comparación ya mencionada y los ejecutamos a través de los mejores solucionadores descritos en el artículo original. Resultados y descripción de las ejecuciones aquí . Tomamos el archivo resultante y construimos un par de gráficos sobre él. Dado que el tiempo de solución varía de milisegundos a decenas de minutos, el gráfico se hace con una escala logarítmica.
correr en la computadora portátil jupyter import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline
solucionador de python
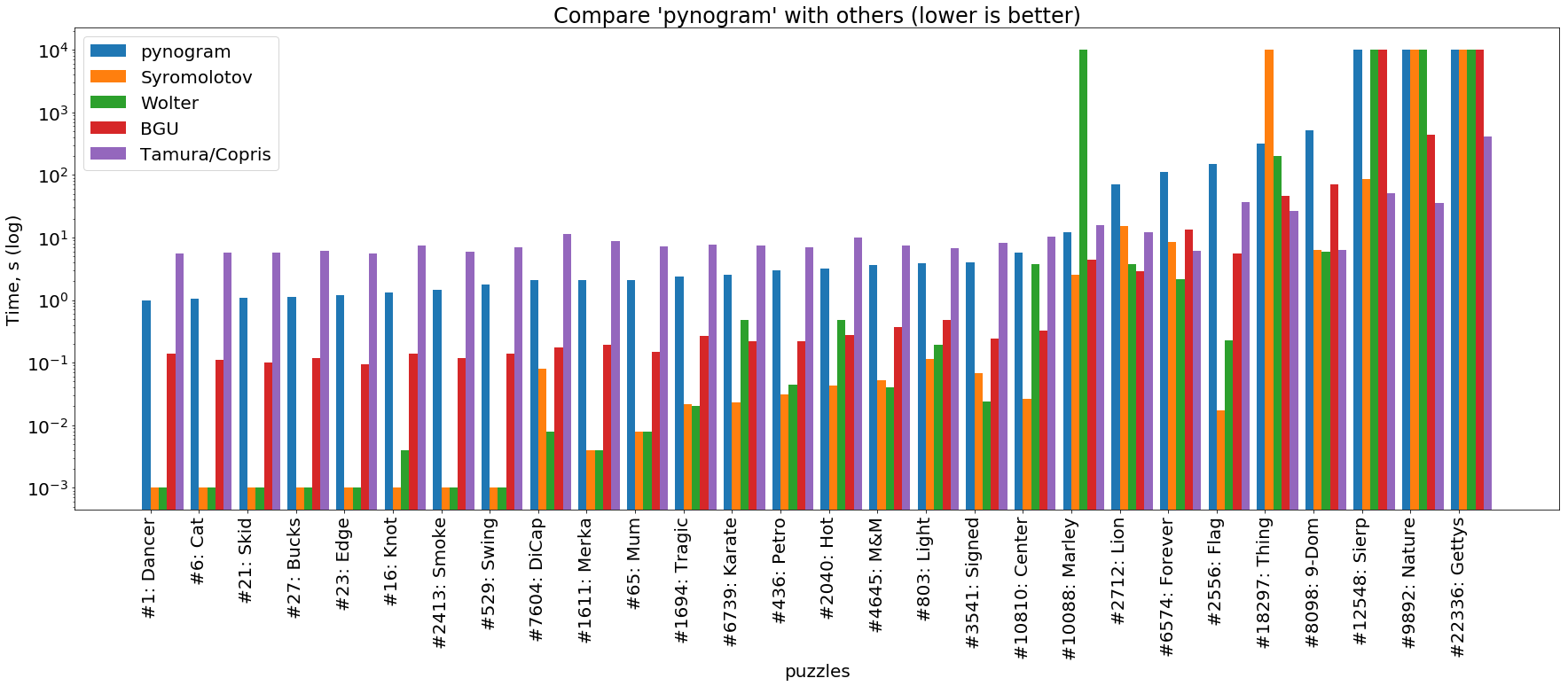
( se puede hacer clic en la imagen )
Vemos que el pynogram aquí es más lento que todos los solucionadores presentados. La única excepción a esta regla es el solucionador Tamura / Copris basado en SAT, que resuelve los acertijos más simples (la parte izquierda del gráfico) por más tiempo que el nuestro. Sin embargo, esta es una característica de los solucionadores de SAT: están diseñados para crucigramas súper complejos en los que un solucionador regular se atasca en el retroceso durante mucho tiempo. Esto es claramente visible en el lado derecho del gráfico, donde Tamura / Copris resuelve los acertijos más difíciles decenas y cientos de veces más rápido que todos los demás.
solucionador de óxido
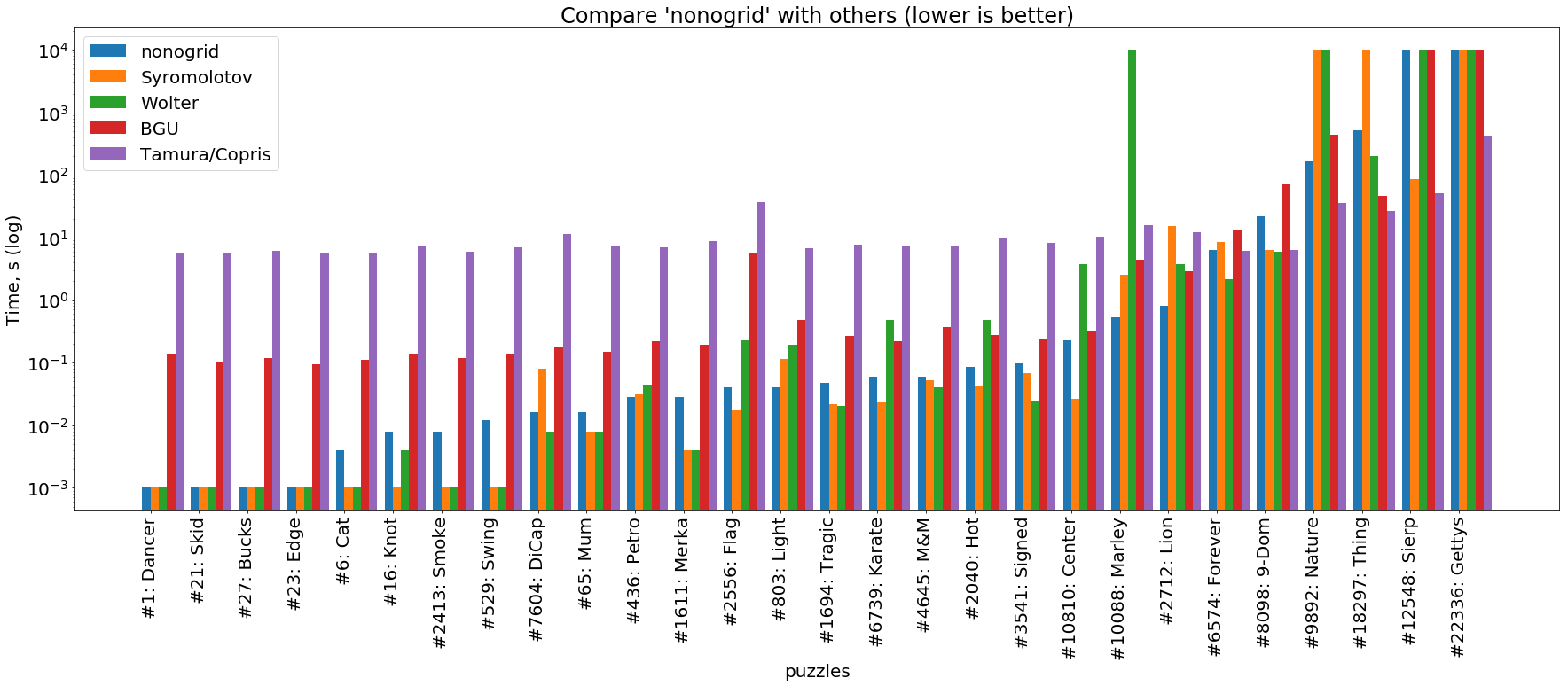
( se puede hacer clic en la imagen )
Este gráfico muestra que la no cuadrícula en tareas simples también hace frente o es un poco peor que los solucionadores de alto rendimiento escritos en C y C ++ ( Wolter y Syromolotov ). Con la complicación de las tareas, nuestro solucionador repite aproximadamente la trayectoria del solucionador BGU (Java), pero casi siempre por delante en un orden de magnitud. En las tareas más difíciles, Tamura / Copris siempre está por delante de todos.
óxido vs pitón
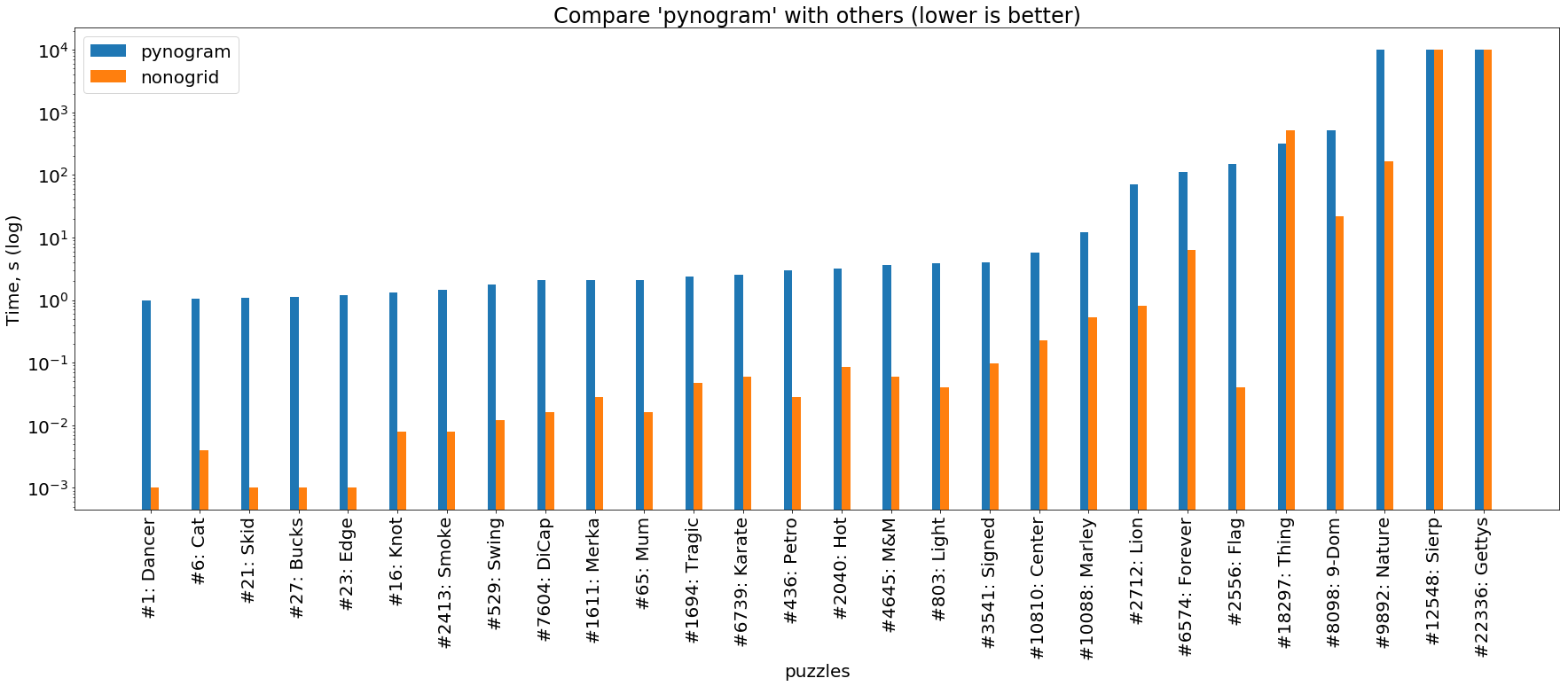
( se puede hacer clic en la imagen )
Y finalmente, una comparación de nuestros dos solucionadores descritos aquí. Se puede ver que el solucionador de óxido casi siempre tiene 1-3 órdenes de magnitud por delante del solucionador de pitón.
+ solucionador puede resolver todos los rompecabezas de los sitios https://webpbn.com (excepto los borrados, con tamaños de bloque parcialmente ocultos), http://nonograms.org y su propio formato (basado en TOML)
+ resuelve nonogramas en blanco y negro y en color con cualquier cantidad de colores
+ puede hacer rompecabezas en la consola (color c webpbn.com dibuja color real)
+ funciona rápido (en comparación con las implementaciones descritas en la comparación de artículos de solucionadores, ver tabla).
- el retroceso ha permanecido ineficaz, como en la solución de Python: algunos acertijos (por ejemplo , un inofensivo 20x20 ) se pueden resolver durante horas (cuando el árbol de decisión es muy grande). Quizás en lugar de retroceder vale la pena usar los solucionadores SAT ya mencionados en el hub Es cierto que el único solucionador de SAT que encontré en Rust a primera vista parece inacabado y abandonado.
Montaje web
Por lo tanto, reescribir el código en Rust ha valido la pena: el solucionador se ha vuelto mucho más rápido. Sin embargo, Rust nos ofrece otra característica increíblemente genial: compilación en WebAssembly y la capacidad de ejecutar su código directamente en el navegador.
Para implementar esta función, hay una herramienta especial para Rust que proporciona los aglutinantes necesarios y genera una plantilla repetitiva para que pueda ejecutar sin problemas las funciones de Rust en el código JS: este paquete wasm (+ wasm-bindgen ). La mayor parte del trabajo con él y otras herramientas importantes ya se describen en el tutorial Rust and WebAssembly . Sin embargo, hay un par de puntos que tuve que resolver por mi cuenta:
cuando lee, crea la sensación de que el tutorial está escrito principalmente para un desarrollador de JS que quiere acelerar su código con Rust. Bueno, o al menos para alguien familiarizado con npm . Para mí, como persona lejos del front-end, fue sorprendente encontrar que incluso el ejemplo estándar del libro no quiere trabajar con un servidor web de terceros que sea diferente de npm run start .
Afortunadamente, wasm-pack tiene un modo que le permite generar código JS regular (que no es un módulo npm). wasm-pack build --target no-modules --no-typescript en la salida solo generará dos archivos: project-name.wasm - el binario del código Rust compilado en WebAssembly y project-name.js . El último archivo se puede agregar a cualquier página HTML <script src="project-name.js"></script> y usar funciones WASM sin molestarse con npm, webpack, ES6, módulos y otras alegrías del desarrollador JS moderno. El modo no-modules es ideal para desarrolladores que no son front-end durante el desarrollo de una aplicación WASM, así como para ejemplos y demostraciones, ya que no requiere ninguna infraestructura front-end adicional.
WebAssembly es bueno para tareas que son demasiado pesadas para JavaScript. En primer lugar, estas son tareas que realizan muchos cálculos. Y si es así, dicha tarea se puede realizar durante mucho tiempo incluso con WebAssembly y, por lo tanto, viola el principio asincrónico de la web moderna. Estoy hablando de todo tipo de Advertencia: secuencia de comandos que no responde que observé cuando mi solucionador funcionaba. Para resolver este problema, puede utilizar el mecanismo de trabajo web . En este caso, el esquema para trabajar con funciones WASM "pesadas" puede verse así:
- desde el script principal para un evento (por ejemplo, al hacer clic en un botón), envíe un mensaje al trabajador con la tarea de iniciar una función pesada.
- , .
- - ()
WASM- JS, WASM . - ( ), HashMap , . ( JS) , / .
, Mutex , thread-safe. smart- . thread-safe Rc Arc RefCell RwLock . : 30%. --features=threaded thread-safe , WASM-.
6574 8098 ( 10 ):
, - 40..70% , , (32..37%) thread-safe ( cargo build --release --features=threaded ).
Firefox 67.0 Chromium 74.0.
WASM- ( ). https://webpbn.com/ http://www.nonograms.org/
TODO
"" /, / .
, . "" , , . .
( , 3600 ). WASM , ( , (!) , , WASM). , , - , nonogrid .
. : , , WASM . , ( ) , JS , .
JS. backtrace, .
( TOML- )
Resumen
, (, , etc).
Rust 1-3 PyPy 1.5-2 ( ).
Python Rust , Python (, , comprehensions), Rust-.
Rust WebAssembly . Rust , WASM, ( 1.5 ).
- The 'pbnsolve' Paint-by-Number Puzzle Solver by Jan Wolter and the survey
- The BGU Nonograms Project
- Solving Nonograms by combining relaxations
- An Efficient Approach to Solving Nonograms
- Color and black and white Japanese crosswords on-line
- 'Nonolib' library by Dr. Steven Simpson
- Rust and WebAssembly