Juega Tetris en AR

Se me ocurrió una extraña idea de que la casa podría ser una buena plataforma para jugar Tetris. No muy lejos de mí, solo había un edificio adecuado para esto. El resultado se puede ver en el video:


El proyecto se implementa a un nivel bastante bajo, sin utilizar ninguna solución preparada.

Código fuente

La mayoría de las veces usan 2 opciones para implementar la realidad aumentada:

• sin marcador, es decir la posición de la cámara está determinada por el movimiento de los puntos clave de su transmisión de video;
• imagen como marcador relativo a la posición de la cámara.

Estas implementaciones no requieren preparación especial o condiciones especiales.

Hay otra opción de implementación: reconocer un objeto específico y usarlo como marcador. Esto requiere al menos su presencia, pero hace posible controlarlo visualmente. Uno de los métodos de dicho reconocimiento es la detección de un objeto por bordes. Tiene limitaciones: el objeto marcador debe tener bordes claramente definidos, es decir el objeto probablemente debería ser sólido.

O los bordes deben estar claramente delineados, como la iluminación de este edificio:



Se puede ver que la luz de fondo puede separarse fácilmente en la imagen y usarse para la detección.

Implementación

En Qt. Este marco le permite trabajar en diferentes plataformas y al mismo tiempo en C ++. Como el rendimiento es importante para nosotros, los profesionales parecen una opción obvia.

Aunque Qt no funcionó muy bien con Android (lanzamiento prolongado, la depuración se deshabilitó), pero todo se estabilizó por la capacidad de depurar el algoritmo en el escritorio.

Se visualizaron gráficos tridimensionales en el OpenGL sin procesar incrustado en Qt.

El trabajo con la cámara se realizó a través de Qt. Se grabó un video para la depuración, y fue lo suficientemente conveniente como para reemplazar la transmisión de video de la cámara con una transmisión de video de un archivo.

La salida se realizó a través de herramientas qml. Hacer amigos qml y OpenGL no estuvo exento de problemas, pero no nos detendremos en esto.

Para el procesamiento de imágenes, la biblioteca OpenCV está conectada.

Algoritmo de seguimiento

Ahora pasemos a la parte más interesante: el algoritmo para rastrear un objeto a lo largo de sus bordes.
Y comience resaltando los bordes de la imagen. Todos los bordes en nuestro caso tienen la forma de líneas rectas, por lo que el primer pensamiento que viene a la mente es usar un detector de línea. Las transformaciones de Hough podrían usarse como un detector de línea. Sin embargo, esta forma me parece poco cierta, ya que la transformación de Hough es bastante costosa, además, este detector no es muy confiable (esto es subjetivo, tal vez todo depende de la tarea).
En cambio, vamos de una manera diferente y más general. No tendremos en cuenta que nuestras líneas son rectas, pero trabajaremos simplemente en una imagen binaria. La presencia de bordes se codificará en la imagen binaria. Es decir un píxel con un valor de cero significa que hay un borde en este lugar, el valor del píxel es mayor que cero, no hay borde. Dicha imagen se puede obtener usando un detector de límites Canny o usando una transformación de umbral simple. Estos algoritmos se pueden encontrar en OpenCV.

También en OpenCV hay otra función que nos resulta útil ahora: distanceTransform , que toma una imagen binaria en la entrada y proporciona una imagen en la salida, en cuyos píxeles se codifica la distancia al píxel cero más cercano.

Ahora supongamos que ya tenemos la primera buena aproximación de dónde debe ubicarse nuestro modelo. A continuación, describimos la función de error, que describe hasta qué punto los bordes de nuestra aproximación no coinciden con los bordes en la imagen resultante. Usando la imagen de distanceTransform ya podemos hacer esto. Y luego ejecutamos el algoritmo de optimización de funciones, cambiando solo nuestra aproximación de la posición del objeto en el espacio. Como resultado, nuestra aproximación debería describir con bastante precisión la posición real del objeto.
Como resultado, el algoritmo se puede dividir en dos etapas:

1. Preprocesamiento de imágenes: binarización, filtrado y uso de la función distanceTransfrom.
2. Seguimiento: optimización de la función de error.

Preprocesamiento de imagen

En este punto, debe resaltar los bordes de la imagen. Puede usar el detector de límites Canny, pero en nuestro caso la conversión de umbral habitual o su versión adaptativa funciona mejor (en OpenCV estas son funciones de umbral o umbral adaptativo). Está claro que habrá ruido en dicha imagen, por lo que se necesita filtrado. Hagámoslo de la siguiente manera: seleccione el contorno utilizando la función OpenCV findCountours y elimine segmentos que son demasiado pequeños o no lo suficientemente como una línea.

El resultado del procesamiento se puede ver en la imagen:



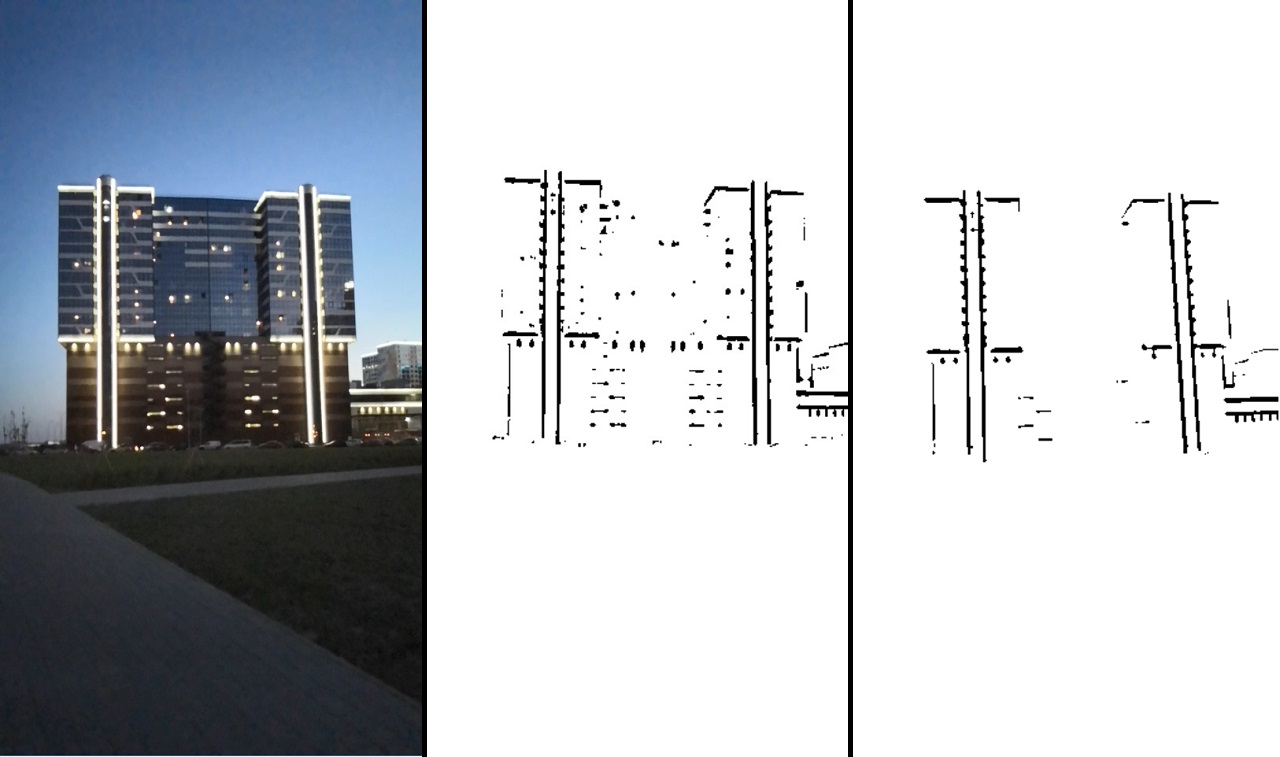
Consistentemente: la imagen original -> después de la transformación del umbral -> después del filtrado.

Esta imagen ya nos dice claramente dónde está el borde derecho y dónde no. Después de eso, usamos la función distanceTransform, y como resultado, tendremos información sobre qué tan lejos está cada punto del borde. La imagen resultante se denota como .

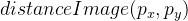
Así es como se ve si se normaliza y visualiza:



A continuación, necesitaremos algunas herramientas matemáticas.

Algoritmo de optimización de funciones

La optimización de funciones es la tarea de encontrar el mínimo de una función.

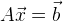
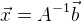
Si estamos tratando con un sistema lineal de ecuaciones, encontrar un mínimo es bastante simple. Imagine el sistema de ecuaciones en forma de matriz: , entonces nuestra solución: . Si tenemos un sistema de ecuaciones sobredeterminado, entonces podemos usar el método de mínimos cuadrados : .

Si nuestra función no es lineal, la tarea se vuelve más complicada. Para encontrar el mínimo, puede usar el algoritmo de Gauss-Newton . El algoritmo funciona de la siguiente manera:

1. Se supone que ya tenemos una aproximación inicial de la solución. que vamos a refinar iterativamente
2. Usando la expansión de Taylor, podemos aproximar nuestra función no lineal lineal en el punto de aproximación actual. Resolvemos el sistema lineal de ecuaciones resultante por el método de mínimos cuadrados, obteniendo 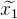. Como resultado, la solución resultante no será una solución, pero estará más cerca que la aproximación actual.
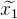3. Reemplazar la aproximación actual decisión recibida y vaya al paso 2. Entonces repita hasta la diferencia entre y No será inferior a un cierto valor.

Analicemos el algoritmo con más detalle.

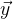
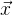
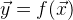
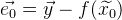
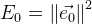
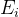
Dejar - función de trabajo, - un vector de valores de función previamente conocido. Con la solución perfecta a la ecuación. la siguiente afirmación es verdadera . Pero solo tenemos su aproximación . Entonces el vector de error de esta aproximación se denota como: . Un error general de la función será: . Ahora encontrando tal en que alcanzará un mínimo, obtendremos una mejor aproximación de la solución .
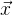
Comenzando desde el enfoque lo aproximaremos iterativamente, obteniendo en cada iteración . Para hacer esto, necesitamos cada iteración para calcular la matriz de Jacobi para la función para la aproximación actual, que consiste en derivados de nuestra función:

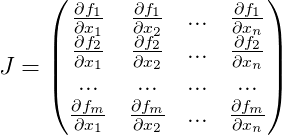
Y la siguiente aproximación se da como: .
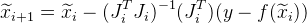
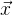
A menudo, las tareas se construyen de tal manera que tenemos una gran cantidad de datos independientes entre sí (solo a partir de los valores ) Como resultado, la matriz general de Jacobi es muy escasa. Hay una manera de optimizar los cálculos.
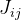
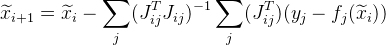
Suponga que una función común se calcula a partir de un conjunto de puntos. Desde el punto j . En lugar de calcular la matriz de Jacobi para toda la función, calculamos la matriz de Jacobi específicamente para y denotarlo como: . Entonces la siguiente aproximación se dará de la siguiente manera: . Además, este cambio le permite paralelizar los cálculos.
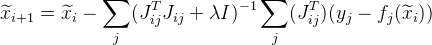
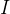
Puede suceder que el siguiente valor dará un error más grande que . Para resolver este problema, puede usar una modificación del algoritmo: el algoritmo Levenberg-Marquardt . Agregar valor en nuestra fórmula: donde Es una matriz unitaria. Valor seleccionado de la siguiente manera:

• primero, tiene un valor bastante pequeño (tal que el algoritmo converge);
• entonces si un error para mas que , luego aumente el valor e intente calcular el error para de nuevo

Cuanto más no lineal es la función cuanto mayor sea el valor . Sin embargo, cuanto mayor sea el valor , más lento converge el algoritmo.

Completamos el algoritmo cuando diferente de lo suficientemente pequeño y tomar como solución

El algoritmo es bastante universal y puede usarse para una variedad de tareas.

Modelo de seguimiento matemático

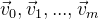
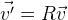
Como estamos tratando con coordenadas en el espacio, está claro que necesitamos poder manipular estas coordenadas. Supongamos que tenemos algún conjunto de puntos . Y necesitamos rotarlos alrededor del punto con coordenadas cero. Probablemente, la forma más fácil sería utilizar la matriz de rotación R , que describe la rotación necesaria: . Si necesitamos cambiar los puntos, simplemente agregue el vector deseado t : .
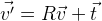
Por lo tanto, puede cambiar arbitrariamente la posición de un objeto en el espacio. Resulta que las coordenadas del objeto están determinadas por la matriz tridimensional R y el vector tridimensional t , es decir. 12 parámetros. Además, estos parámetros no son independientes entre sí, los componentes de la matriz de rotación están interconectados por ciertas condiciones. Por lo tanto, desde el punto de vista del uso de estas funciones en la optimización, estos parámetros no son la mejor solución. Hay más parámetros que grados de libertad, hay una relación entre ellos. Hay otra forma de rotación: la fórmula de rotación de Rodrigue . Esta rotación se especifica mediante tres parámetros, formando un vector tridimensional.

El vector normalizado es el eje de rotación, y la longitud de este vector es el ángulo de rotación alrededor de este eje.

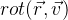
Establecemos la función de rotación del vector v : utilizando los parámetros r de la fórmula Rodrigue. Obtenemos la siguiente fórmula de esto: .
Y al final, podemos establecer las coordenadas de la posición del objeto con un vector de 6 dimensiones:
Obtenemos la siguiente fórmula: .

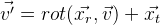
Modelo de cámara estenopeica

Ahora describimos un modelo matemático simple de la cámara utilizada en el proyecto:

$$

$$\ vec {p} = \ begin {pmatrix} p_x & p_y \ end {pmatrix} ^ T = cam (\ vec {v}) = \ begin {pmatrix} f_x \ frac {v_x} {v_z} + c_x & f_y \ frac {v_y} {v_z} + c_y \ end {pmatrix} ^ T$$

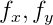
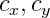
donde - distancia focal en píxeles; - El centro óptico también está en píxeles. Estos son parámetros individuales de la cámara, que se denominan parámetros intrínsecos de la cámara. Típicamente, estos parámetros son conocidos de antemano. En este proyecto, estos parámetros se seleccionan a simple vista.

Este modelo no tiene en cuenta la distorsión del objetivo de las cámaras ( distorsión ). Supongamos que no lo son.

Con este modelo, obtenemos una proyección central, cuyos puntos tienden más hacia el centro óptico, cuanto más lejos están de la cámara. Así obtenemos el efecto de un ferrocarril que se estrecha:



En el espacio, la cámara está alineada con el eje z , el plano de la imagen es paralelo al plano xy . Complementamos nuestro modelo con la capacidad de moverse en el espacio:

$$

$$\ vec {p} _j = cam (rot (\ vec {x} _r, \ vec {v} _j) + \ vec {x} _t)$$

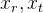
Por lo tanto, obtuvimos un modelo con el que podemos simular en forma algebraica la proyección de puntos del mundo exterior en la imagen de la cámara (desde las coordenadas del mundo a la pantalla). Para nosotros, los parámetros de la posición relativa de la cámara en el espacio siguen siendo desconocidos en este modelo. . Estos parámetros se denominan parámetros extrínsecos de la cámara.

Seguimiento

Implementado ya sin herramientas OpenCV. Primero, necesitamos obtener la función de error para nuestra solución aproximada, que se describió anteriormente. Y escribiremos su cálculo en etapas:

1. Seleccionamos dichos bordes del modelo de seguimiento que son visibles en función de los parámetros de la aproximación actual.
2. Convertimos el conjunto de aristas seleccionado en un conjunto fijo de puntos, para simplificar los cálculos. Es posible, por ejemplo, tomar el enésimo número de puntos de cada borde, o (una opción más correcta) elegir una cantidad tal que haya una distancia fija en píxeles entre los puntos. Los llamaremos puntos de control (en el proyecto: controlPoint - puntos de control y controlPixelDistance - la misma distancia fija en píxeles).
3. Proyectamos puntos de control en la imagen. Gracias a distanceImage, podemos obtener la distancia de la proyección del punto de control al borde de la imagen. En el caso ideal, todos los puntos de control deben estar estrictamente en los bordes de la imagen, es decir. la distancia a la costilla debe ser cero. En base a esto, obtenemos un error para un punto de control específico: .
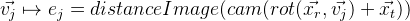4. Obtenemos la siguiente función de error:

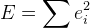
Ahora queda por encontrar un mínimo de E. Para hacer esto, usamos el algoritmo de Levenberg-Marquardt descrito anteriormente. Como ya sabemos, el algoritmo requiere el cálculo de la matriz de Jacobi, es decir. funciones derivadas Puede usar el hallazgo numérico de derivados. También puede usar algunas soluciones listas para este algoritmo. Sin embargo, en este proyecto todo fue escrito manualmente, por lo que describiré la conclusión completa de toda la solución.

Para cada punto de control, obtenemos una ecuación independiente de otros puntos. Ya se ha descrito anteriormente que en este caso es posible considerar estas ecuaciones independientemente una de la otra, calculando la matriz de Jacobi específicamente para cada una. Lo analizaremos en orden, usando las reglas de diferenciación de una función compleja:



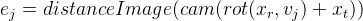
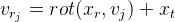
Denotamos entonces



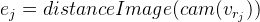
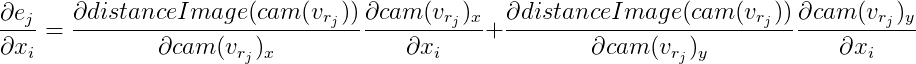
Desde aquí:



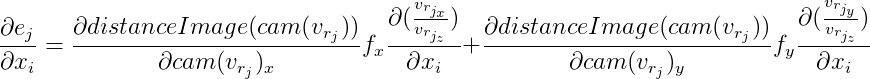
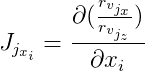
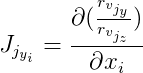
Además denotamos y entonces:


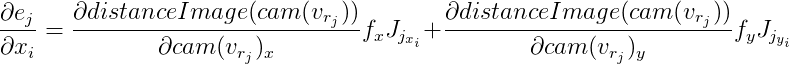
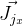
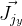
Las derivadas de distanceImage son numéricamente. Y para computar vectores y necesitará encontrar derivados de acuerdo con la fórmula de rotación de Rodrigue. Encontré a Jacobian con esta fórmula en la publicación "Una fórmula compacta para la derivada de una rotación tridimensional en
coordenadas exponenciales »Guillermo Gallego, Anthony Yezzi :

,
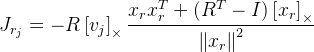
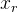
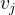
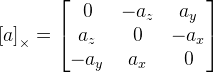
donde R es la matriz de rotación obtenida por la fórmula Rodrigue del vector de rotación ; - el punto que estamos cambiando; I es la matriz de identidad; . Como vemos aquí, tenemos una división por la longitud del vector de rotación, y si el vector es cero, entonces la fórmula ya no funciona. Esto probablemente se deba al hecho de que en el vector cero el eje de rotación no está definido. Si el vector de rotación está muy cerca de cero, entonces usamos esta fórmula: .
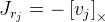
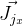
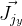
Queda por pintar y (aquí se omite el índice j ):


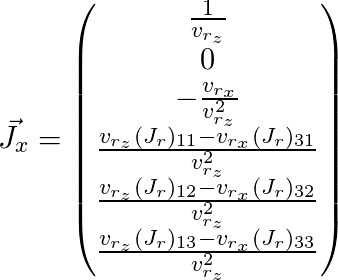
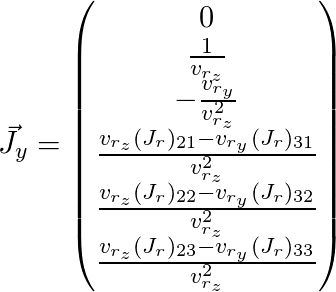
Por lo tanto, obtuvimos la matriz de Jacobi para el punto que necesitamos y podemos usarla para el algoritmo de optimización descrito anteriormente.

Hay varios problemas con este algoritmo. En primer lugar, precisión. Como resultado, la posición global de la cámara salta ligeramente de cuadro a cuadro. Puedes arreglarlo un poco. Tenemos información a priori de que la posición de la cámara no puede cambiar dramáticamente de cuadro a cuadro. Y podemos reducir esta inquietud agregando ecuaciones adicionales a la función.

Debe recordarse que el vector de desplazamiento t no es en nuestro caso la coordenada de la posición global de la cámara. La posición global es un punto local con coordenadas cero, por lo que se puede derivar de la siguiente manera:



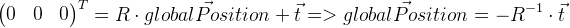
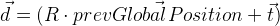
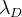
Recordamos la posición del marco anterior en prevGlobalPosition . Ahora la posición anterior debería estar cerca de cero, es decir longitud del vector debería ser lo suficientemente pequeño. Es decir Además de otros valores de discrepancias, el vector d también debe minimizarse. Para determinar el grado de influencia de esta modificación, introducimos el valor y multiplique el vector d sumando por : . 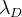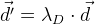Es decir en el algoritmo de optimización, también minimizamos el vector d ' . Por supuesto, para esto será necesario calcular la matriz de Jacobi para ella, que se deriva de la misma manera que ya derivamos anteriormente para la función de error general.

El segundo problema del algoritmo es que puede atascarse en mínimos locales. En otros trabajos, este problema se resuelve utilizando un filtro de partículas. En nuestro caso, esta opción resultó ser, en principio, suficiente.

Bonificaciones por rastrear un objeto

Conociendo la posición y la forma del objeto, puede manipularlos visualmente, lo que intenté demostrar en el video. El objeto fue distorsionado usando sombreadores OpenGL. Con la ayuda de nuestro modelo, proyecté el punto del objeto en la imagen, y así recibí el color de este punto. Luego puede mover este punto, obteniendo efectos interesantes, por ejemplo, morphing. Sin embargo, uno debe recordar que al cambiar el punto, es necesario que algo permanezca en su lugar, de lo contrario las inconsistencias se harán evidentes. Además, dependiendo de la calidad de nuestro seguimiento y la forma del objeto, recibiremos varios efectos indeseables debido a los errores acumulados, que seguirán siendo. Solo debe tenerse en cuenta de alguna manera. En el video presentado anteriormente, quería mostrar que la realidad aumentada puede usarse un poco más que simplemente imponer objetos virtuales en la imagen.

Por cierto, el SDK de Vuforia implementa el seguimiento de un objeto por su forma, aunque no creo que sea posible implementar este proyecto con él, ya que no es posible usar bordes estrictamente definidos y no puede asociarse con la iluminación del edificio.