Un artículo del equipo de Stitch Fix sugiere utilizar un enfoque de investigación clínica de ensayos de no inferioridad en las pruebas A / B de marketing y productos. Este enfoque es realmente aplicable cuando probamos una nueva solución que tiene ventajas que las pruebas no pueden medir.
El ejemplo más simple es la pérdida ósea. Por ejemplo, automatizamos el proceso de asignación de la primera lección, pero no queremos perder mucho la conversión directa. O probamos los cambios que se centran en un segmento de usuarios, al tiempo que nos aseguramos de que las conversiones en otros segmentos no se hundan mucho (al probar varias hipótesis, no se olvide de las correcciones).
Elegir el borde derecho de no menos eficiencia agrega dificultades adicionales en la etapa de diseño de la prueba. La cuestión de cómo elegir Δ en el artículo no está bien revelada. Parece que esta elección no es completamente transparente en ensayos clínicos.
Una revisión de publicaciones médicas sobre informes de no inferioridad indica que en solo la mitad de las publicaciones la elección del borde está justificada y, a menudo, estas justificaciones son ambiguas o no detalladas.
En cualquier caso, este enfoque parece interesante, porque Al reducir el tamaño de muestra requerido, puede aumentar la velocidad de las pruebas y, por lo tanto, la velocidad de la toma de decisiones. -
Daria Mukhina, analista de productos para la aplicación móvil Skyeng.Al equipo de Stitch Fix le encanta probar cosas diferentes. A toda la comunidad tecnológica, en principio, le gusta realizar pruebas. ¿Qué versión del sitio atrae a más usuarios, A o B? ¿La versión A del modelo de recomendación trae más dinero que la versión B? Casi siempre, para probar hipótesis, utilizamos el enfoque más simple de un curso básico de estadística:
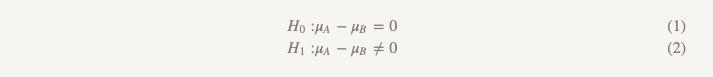
Aunque raramente usamos el término, esta forma de prueba se llama "hipótesis de prueba de superioridad". Con este enfoque, asumimos que no hay diferencia entre las dos opciones. Nos adherimos a esta idea y la rechazamos solo si los datos obtenidos son lo suficientemente convincentes para esto, es decir, demuestran que una de las opciones (A o B) es mejor que la otra.
Probar la hipótesis de la superioridad es adecuado para resolver muchos problemas. Lanzamos la versión B del modelo de recomendación solo si es obviamente mejor que la versión A ya utilizada, pero en algunos casos este enfoque no funciona tan bien. Veamos algunos ejemplos.
1) Utilizamos un servicio de terceros que ayuda a identificar tarjetas bancarias falsas. Encontramos otro servicio que cuesta significativamente menos. Si un servicio más barato funciona tan bien como el que usamos ahora, lo elegiremos. No tiene que ser mejor que el servicio utilizado.
2) Queremos abandonar la fuente de datos A y reemplazarla con la fuente de datos B. Podríamos retrasar el abandono de A si B produce resultados muy pobres, pero no es posible continuar usando A.
3) Nos gustaría pasar del enfoque al modelado A al enfoque B no porque esperemos mejores resultados de B, sino porque nos brinda una gran flexibilidad operativa. No tenemos razones para creer que B será peor, pero no comenzaremos la transición si este es el caso.
4) Hicimos varios cambios cualitativos en el diseño del sitio web (versión B) y creemos que esta versión es superior a la versión A. No esperamos cambios en la conversión ni ningún indicador clave de rendimiento por el cual generalmente evaluamos el sitio web. Pero creemos que hay ventajas en los parámetros que son inconmensurables o que nuestras tecnologías no son suficientes para medir.
En todos estos casos, investigar la excelencia no es la mejor solución. Pero la mayoría de los expertos en estas situaciones lo usan por defecto. Cuidadosamente llevamos a cabo un experimento para determinar correctamente la magnitud del efecto. Si fuera cierto que las versiones A y B funcionan de manera muy similar, existe la posibilidad de que no podamos rechazar la hipótesis nula. ¿Concluimos que A y B generalmente funcionan igual? No! La incapacidad de rechazar la hipótesis nula y la adopción de la hipótesis nula no son lo mismo.
Los cálculos del tamaño de la muestra (que, por supuesto, usted realizó) generalmente se llevan a cabo con límites más estrictos para el primer error amable (probabilidad de rechazo erróneo de la hipótesis nula, a menudo llamada alfa), que para el segundo error amable (probabilidad de no rechazar la hipótesis nula, cuando suponiendo que la hipótesis nula es incorrecta, a menudo llamada beta). El valor típico para alfa es 0.05, mientras que el valor típico para beta es 0.20, que corresponde a una potencia estadística de 0.80. Esto significa que con nosotros no podemos detectar la verdadera influencia del valor que indicamos en nuestros cálculos de potencia con una probabilidad del 20% y esta es una brecha de información bastante seria. Como ejemplo, consideremos las siguientes hipótesis:
H0: mi mochila NO está en mi habitación (3)
H1: mi mochila está en mi habitación (4)Si busqué en mi habitación y encontré mi mochila, bien, puedo rechazar la hipótesis nula. Pero si miré alrededor de la habitación y no pude encontrar mi mochila (Figura 1), ¿qué conclusión debo sacar? ¿Estoy seguro de que no está allí? ¿He buscado lo suficiente? ¿Qué pasa si busqué solo el 80% de la habitación? Llegar a la conclusión de que la mochila definitivamente no está en la habitación será una decisión precipitada. No es sorprendente que no podamos "aceptar la hipótesis nula".
El área que buscamos
No encontramos una mochila, ¿deberíamos aceptar la hipótesis nula?Figura 1. Buscar el 80% de la sala es casi lo mismo que realizar un estudio con una capacidad del 80%. Si no encontró una mochila, después de examinar el 80% de la habitación, ¿es posible concluir que no está allí?Entonces, ¿qué hace un especialista en datos en esta situación? Puede aumentar considerablemente el poder de investigación, pero luego necesitará una muestra mucho más grande y el resultado seguirá siendo insatisfactorio.
Afortunadamente, estos problemas han sido estudiados durante mucho tiempo en el mundo de la investigación clínica. El medicamento B es más barato que el medicamento A; se espera que el medicamento B cause menos efectos secundarios que el medicamento A; el medicamento B es más fácil de transportar porque no necesita almacenarse en el refrigerador y se necesita el medicamento A. Probamos la hipótesis de no menos eficiencia. Esto es necesario para demostrar que la versión B es tan buena como la versión A, al menos dentro de un cierto límite predeterminado de "no menos eficiencia", Δ. Un poco más adelante hablaremos más sobre cómo establecer este límite. Pero ahora suponga que esta es la diferencia más pequeña que es prácticamente significativa (en el contexto de los ensayos clínicos, esto generalmente se llama relevancia clínica).
Las hipótesis de no menos eficiencia vuelven todo al revés:
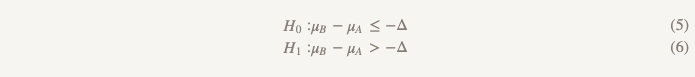
Ahora, en lugar de suponer que no hay diferencia, asumimos que la versión B es peor que la versión A, y mantendremos este supuesto hasta que demostremos que no lo es. ¡Este es exactamente el momento en que tiene sentido usar la prueba de una hipótesis unilateral! En la práctica, esto se puede hacer construyendo un intervalo de confianza y determinando si el intervalo es realmente mayor que Δ (Figura 2).
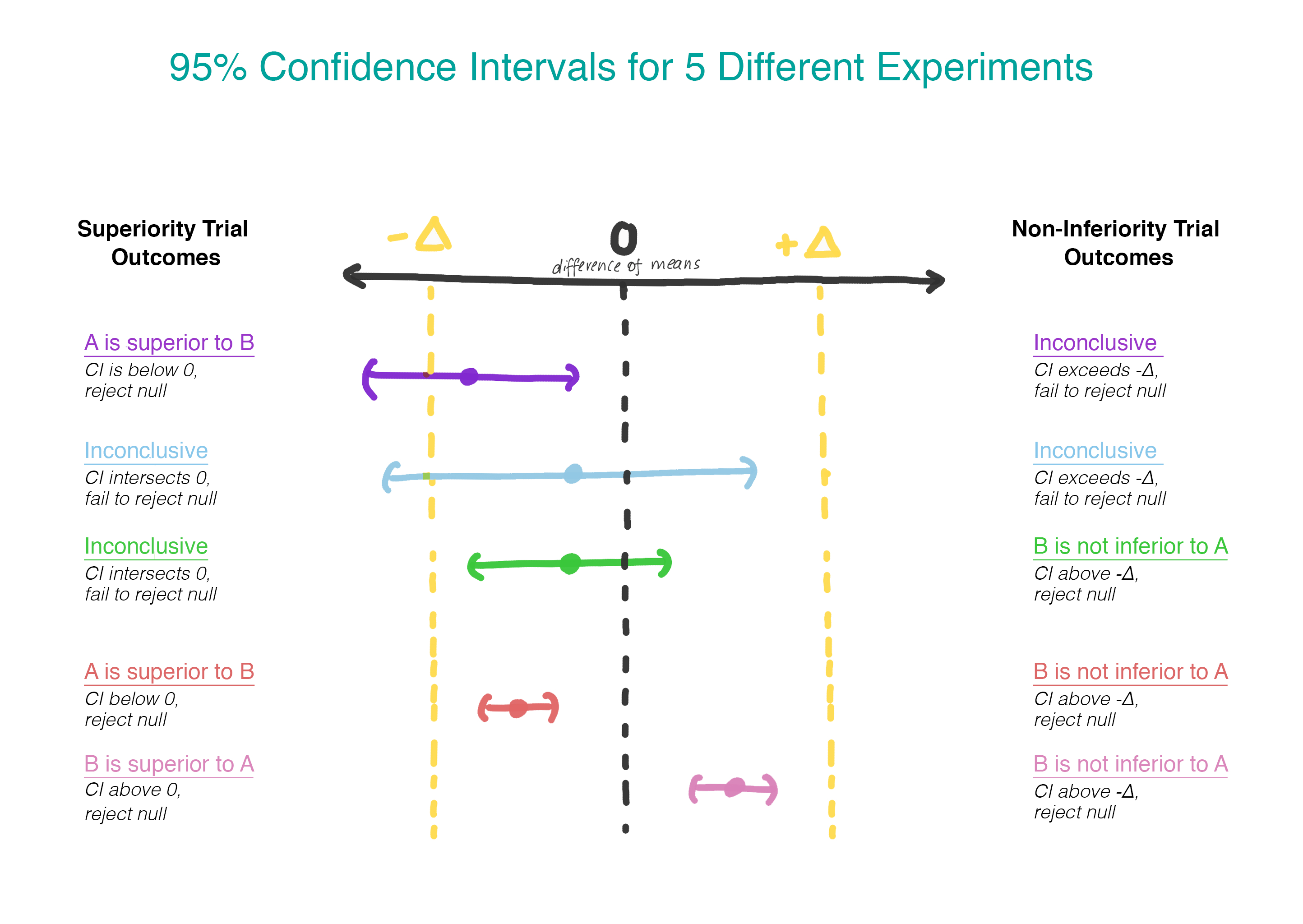
Selección Δ
¿Cómo elegir Δ? El proceso de selección Δ incluye una justificación estadística y una evaluación del tema. Existen recomendaciones normativas en el mundo de los ensayos clínicos, de lo que se deduce que el delta debería ser la diferencia clínicamente más pequeña, una que será relevante en la práctica. Aquí hay una cita de los líderes europeos, con la que puede comprobar usted mismo: “Si la diferencia se eligió correctamente, un intervalo de confianza que se encuentra completamente entre –∆ y 0 ... sigue siendo suficiente para demostrar no menos eficiencia. Si este resultado no parece aceptable, significa que ∆ no se eligió adecuadamente ".
El delta definitivamente no debe exceder la magnitud del efecto de la versión A en relación con el control verdadero (placebo / falta de tratamiento), ya que esto nos lleva a creer que la versión B es peor que el control verdadero, y al mismo tiempo demuestra "no menos eficiencia". Supongamos que cuando se introdujo la versión A, la versión 0 estaba en su lugar o la función no existía (ver Figura 3).
En base a los resultados de probar la hipótesis de superioridad, se reveló la magnitud del efecto E (es decir, presumiblemente μ ^ A - μ ^ 0 = E). Ahora A es nuestro nuevo estándar, y queremos asegurarnos de que B no sea inferior a A. Otra forma de escribir μB - μA≤ - Δ (hipótesis nula) es μB≤μA - Δ. Si suponemos que hacer es igual o mayor que E, entonces μB ≤ μA - E ≤ placebo. Ahora vemos que nuestra estimación para μB excede completamente μA - E, lo que refuta completamente la hipótesis nula y nos permite concluir que B no es inferior a A, pero al mismo tiempo, μB puede ser ≤ μ placebo, pero esto no es que necesitamos (figura 3).
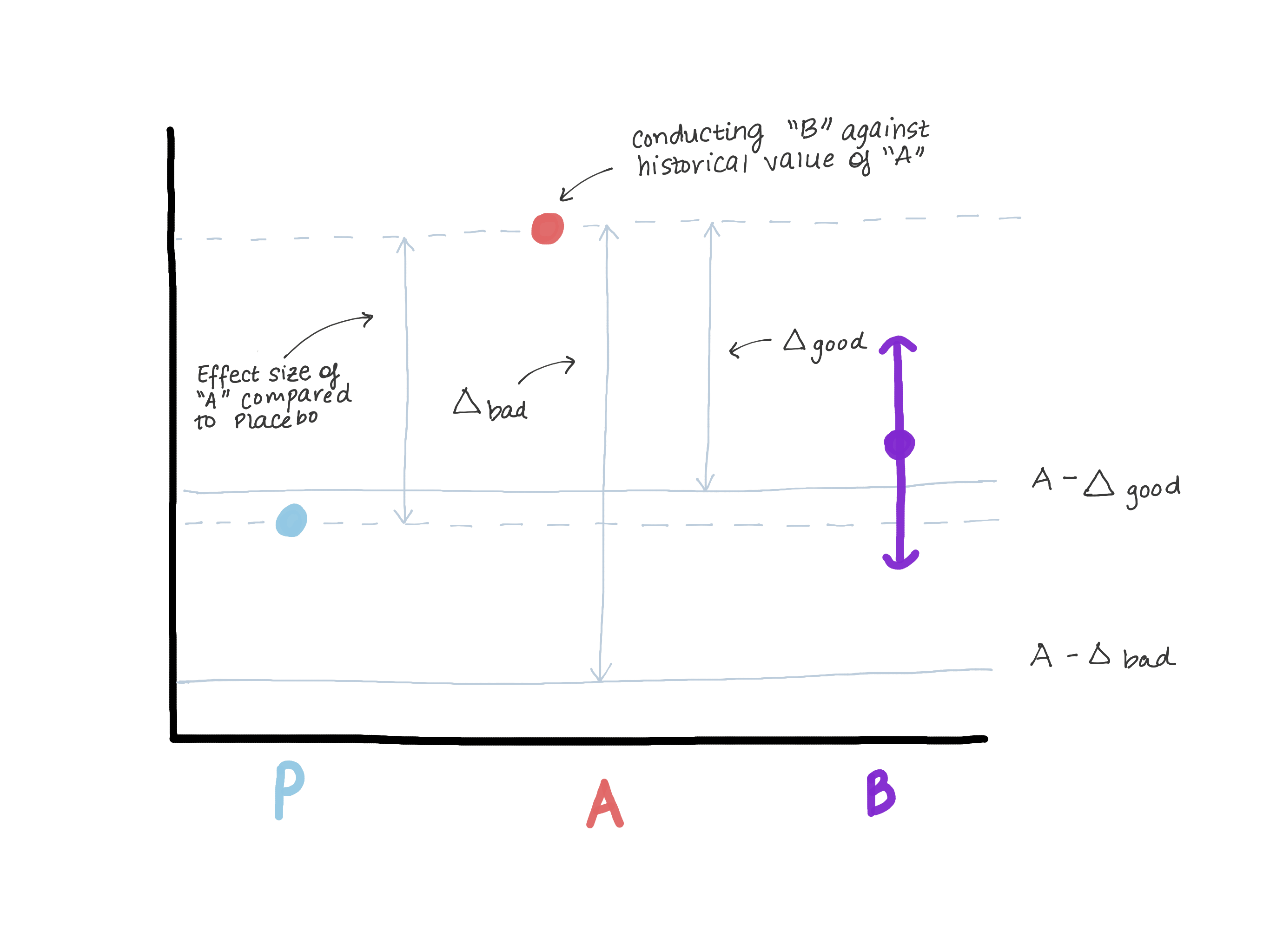Figura 3. Demostración de los riesgos de elegir un borde de no menos eficiencia. Si el límite es demasiado grande, podemos concluir que B no es inferior a A, pero al mismo tiempo es indistinguible del placebo. No cambiaremos el medicamento, que es claramente más efectivo que el placebo (A), en el medicamento, que tiene la misma efectividad que el placebo.Elegir α
Pasamos a la elección de α. Puede usar el valor estándar α = 0.05, pero esto no es del todo honesto. Por ejemplo, cuando compra algo en Internet y usa varios códigos de descuento a la vez, aunque no deben resumirse, el desarrollador simplemente cometió un error y usted se salió con la suya. De acuerdo con las reglas, el valor de α debería ser igual a la mitad del valor de α, que se utiliza para probar la hipótesis de superioridad, es decir, 0.05 / 2 = 0.025.
Tamaño de la muestra
¿Cómo estimar el tamaño de la muestra? Si cree que la verdadera diferencia promedio entre A y B es 0, entonces el cálculo del tamaño de la muestra será el mismo que cuando se prueba la hipótesis de superioridad, excepto que reemplaza el tamaño del efecto con un límite de no menos eficiencia, siempre que use
α no menos eficiencia = 1/2 superioridad (αno-inferioridad = 1/2 superior). Si tiene razones para creer que la opción B puede ser ligeramente peor que la opción A, pero desea demostrar que es peor en no más de Δ, ¡entonces está de suerte! De hecho, esto reduce el tamaño de su muestra, porque es más fácil demostrar que B es peor que A si realmente piensa que es ligeramente peor y no equivalente.
Ejemplo de solución
Suponga que desea actualizar a la versión B, siempre que sea peor que la versión A en no más de 0.1 puntos en una escala de satisfacción del cliente de 5 puntos ... Abordaremos esta tarea utilizando la hipótesis de la superioridad.
Para probar la hipótesis de superioridad, calcularíamos el tamaño de la muestra de la siguiente manera:
Es decir, si tiene 2103 observaciones en su grupo, puede estar 90% seguro de que encontrará un efecto de 0.10 o más. Pero si el valor de 0.10 es demasiado grande para usted, quizás no debería probar la hipótesis de superioridad. Quizás, para mayor confiabilidad, decida realizar un estudio para un tamaño de efecto más pequeño, por ejemplo, 0.05. En este caso, necesitará 8407 observaciones, es decir, la muestra aumentará casi 4 veces. Pero, ¿qué sucede si nos atenemos a nuestro tamaño de muestra original, pero aumentamos la potencia a 0,99 para no dudar si obtenemos un resultado positivo? En este caso, n para un grupo será 3676, que es mejor, pero aumenta el tamaño de la muestra en más del 50%. Y como resultado, de todos modos simplemente no podemos refutar la hipótesis nula y no obtenemos la respuesta a nuestra pregunta.
¿Qué pasa si, en cambio, probamos la hipótesis de no menos efectividad?
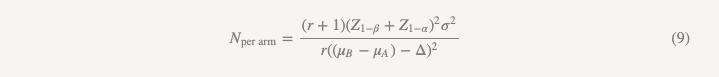
El tamaño de la muestra se calculará utilizando la misma fórmula con la excepción del denominador.
Las diferencias con la fórmula utilizada para probar la hipótesis de superioridad son las siguientes:
- Z1 - α / 2 se reemplaza por Z1 - α, pero si hace todo de acuerdo con las reglas, reemplaza α = 0.05 con α = 0.025, es decir, este es el mismo número (1.96)
- aparece en el denominador (μB - μA)
- θ (magnitud del efecto) se reemplaza por Δ (límite de no menos eficiencia)
Si suponemos que µB = µA, entonces (µB - µA) = 0 y calcular el tamaño de la muestra para un límite de no menos eficiencia es exactamente lo que obtendríamos al calcular la superioridad para el valor del efecto de 0.1, ¡genial! Podemos realizar un estudio de la misma escala con diferentes hipótesis y un enfoque diferente de las conclusiones, y obtendremos una respuesta a la pregunta que realmente queremos responder.
Ahora supongamos que realmente no pensamos que µB = µA y
creemos que µB es un poco peor, quizás 0.01 unidades. Esto aumenta nuestro denominador, reduciendo el tamaño de la muestra por grupo a 1737.
¿Qué sucede si la versión B es realmente mejor que la versión A? Rechazamos la hipótesis nula de que B es peor que A en más de Δ y aceptamos la hipótesis alternativa de que B, si es peor, no es peor que Δ, y podría ser mejor. Intente poner esta conclusión en una presentación multifuncional y vea qué se obtiene (en serio, pruébelo). En una situación en la que necesita concentrarse en el futuro, nadie quiere aceptar "peor por no más de Δ y, posiblemente, mejor".
En este caso, podemos realizar un estudio, que se llama muy brevemente "probar la hipótesis de que una de las opciones es superior a la otra o inferior a ella". Utiliza dos conjuntos de hipótesis:
El primer conjunto (lo mismo que cuando se prueba la hipótesis de no menos eficiencia):
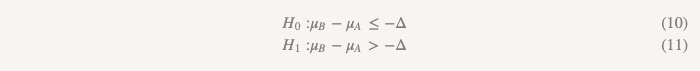
El segundo conjunto (lo mismo que cuando se prueba la hipótesis de superioridad):
Probamos la segunda hipótesis solo si la primera es rechazada. En las pruebas secuenciales, mantenemos el nivel general de errores del primer tipo (α). En la práctica, esto se puede lograr creando un intervalo de confianza del 95% para la diferencia entre las medias y comprobando para determinar si el intervalo completo excede -Δ. Si el intervalo no excede -Δ, no podemos rechazar el valor cero y detenernos. Si todo el intervalo realmente excede −Δ, continuamos y vemos si el intervalo contiene 0.
Hay otro tipo de investigación que no hemos discutido: los estudios de equivalencia.
Los estudios de este tipo pueden ser reemplazados por estudios para probar la hipótesis de no menos efectividad y viceversa, pero de hecho tienen una diferencia importante. Una prueba para probar la hipótesis de no menos eficiencia apunta a demostrar que la opción B es al menos tan buena como A. Y un estudio de equivalencia apunta a mostrar que la opción B es al menos tan buena como A, y la opción A es tan buena como B, que es más complicada. En esencia, estamos tratando de determinar si todo el intervalo de confianza radica en la diferencia de medias entre −Δ y Δ. Dichos estudios requieren un tamaño de muestra mayor y son menos frecuentes. Por lo tanto, la próxima vez que realice un estudio en el que su tarea principal sea asegurarse de que la nueva versión no sea peor, no se conforme con la "incapacidad para refutar la hipótesis nula". Si desea probar una hipótesis realmente importante, considere varias opciones.