El libro "Machine Learning: Algorithms for Business"

Hola habrozhiteli! Marcos López de Prado comparte lo que generalmente esconden: los algoritmos de aprendizaje automático más rentables que ha utilizado durante dos décadas para administrar grandes fondos de los inversores más exigentes.

El aprendizaje automático cambia casi todos los aspectos de nuestras vidas; los algoritmos MO realizan tareas en las que, hasta hace poco, solo confiaban expertos de confianza. En el futuro cercano, el aprendizaje automático dominará las finanzas, la adivinación será cosa del pasado y las inversiones ya no serán sinónimo de juegos de azar.

Aproveche la oportunidad de participar en la "revolución de la máquina", para esto basta con familiarizarse con el primer libro, que proporciona un análisis completo y sistemático de los métodos de aprendizaje automático en relación con las finanzas: comenzando con estructuras de datos financieros, marcando las series financieras, sopesando la muestra, diferenciando las series de tiempo ... y terminando con toda la parte dedicada a la correcta prueba de estrategias de inversión.

Extracto Comprender las estrategias de riesgo

15.1 Relevancia

Las estrategias de inversión a menudo se implementan en términos de posiciones mantenidas hasta que se cumpla una de las dos condiciones: 1) la condición para dejar la posición con ganancias (tomar ganancias) o 2) la condición para dejar la posición con pérdidas (detener la pérdida). Incluso cuando la estrategia no declara explícitamente un tope de pérdida, siempre hay un límite de tope de pérdida implícito en el que el inversor ya no puede financiar su posición (llamada de margen) o incurre en daños causados ​​por un aumento en la pérdida no realizada. Como la mayoría de las estrategias tienen (explícita o implícitamente) estas dos condiciones de salida, tiene sentido modelar la distribución de resultados a través de un proceso binomial. Esto, a su vez, nos ayudará a comprender qué combinaciones de tasas de apuestas, riesgos y pagos no son económicos. El propósito de este capítulo es ayudarlo a evaluar cuándo una estrategia es vulnerable a pequeños cambios en cualquiera de estas cantidades.

Considere una estrategia que produzca n apuestas anualmente distribuidas de forma idéntica e independientes, donde el resultado Xi de la apuesta i ∈ [1, n] representa la ganancia π> 0 con probabilidad P [Xi = π] = p y pérdida –π con probabilidad P [Xi = –Π] = 1 - p. Puede imaginarse p como la precisión de un clasificador binario, en el que un resultado afirmativo significa apostar por la oportunidad, y un resultado negativo significa una oportunidad perdida: las declaraciones verdaderas son recompensadas, las declaraciones falsas son castigadas y los resultados negativos (ya sean verdaderos o falsos) no tienen resultados. Como los resultados de las apuestas {Xi} i = 1, ..., n son independientes, calcularemos los momentos esperados por apuesta. El beneficio esperado de una apuesta es E [Xi] = πp + (–π) (1 - p) = π (2p - 1). 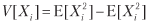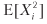La varianza es donde = π2p + (–π) 2 (1 - p) = π2, por lo tanto, V [Xi] = π2 - π2 (2p - 1) 2 = π2 [1– (2p - 1) 2] = 4π2p (1 - p ) Para n tasas de distribución mutuamente independientes e idénticas por año, el índice promedio anual de Sharpe (θ) es


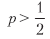
Observe cómo π equilibra la ecuación anterior porque los pagos son simétricos. Como en el caso gaussiano, θ [p, n] puede entenderse como un valor t reescalado1. Esto ilustra el hecho de que incluso para pequeños la relación de Sharpe se puede hacer alta para un n suficientemente grande. Esto sirve como la base económica para el comercio de alta frecuencia, donde p puede ser ligeramente superior a .5, y la clave para una actividad de intercambio exitosa es un aumento en n. La relación de Sharpe es una función de precisión y no de corrección, porque perder una oportunidad (declaración negativa) no se recompensa o castiga directamente (aunque demasiadas declaraciones negativas pueden conducir a una n pequeña, lo que reducirá el coeficiente de Sharpe a cero).

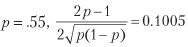
Por ejemplo, para y para alcanzar un promedio anual de Sharpe de 2, se requieren 396 apuestas por año. El listado 15.1 verifica este resultado experimentalmente. La figura 15.1 muestra la relación de Sharpe en función de la precisión para diferentes frecuencias de apuesta.

Listado 15.1. Proporción de Sharpe en función del número de apuestas.

out,p=[],.55 for i in xrange(1000000): rnd=np.random.binomial(n=1,p=p) x=(1 if rnd==1 else -1) out.append(x) print np.mean(out),np.std(out),np.mean(out)/np.std(out) 

Esta ecuación expresa con bastante claridad la compensación entre precisión (p) y frecuencia (n) para un determinado coeficiente de Sharpe (θ). Por ejemplo, para dar un promedio de Sharpe anual de 2 para una estrategia que produce solo tasas semanales (n = 52), se requerirá una precisión bastante alta p = 0.6336.

15.3 Pagos asimétricos

Considere una estrategia que produce n apuestas mutuamente independientes distribuidas de manera idéntica por año, donde el resultado Xi de la apuesta i ∈ [1, n] es π + con probabilidad P [Xi = π +] = p, y el resultado π– (π– <π + ) sucede con probabilidad P [Xi = π_] = 1 - p. El beneficio esperado de una apuesta es E [Xi] = pπ + + (1 - p) π– = (π + - π–) p + π–. La dispersión es V [Xi] =, donde



Finalmente, podemos resolver la ecuación anterior para 0 ≤ p ≤ 1 y obtener


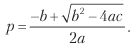
donde:
a = (n + θ2) (π + - π–) 2;
b = [2nπ - θ2 (π + - π -)] (π + - π–);


Nota: El Listado 15.2 verifica estas operaciones simbólicas utilizando el shell Python SymPy Live que se ejecuta en el servicio en la nube de Google App Engine: live.sympy.org .

Listado 15.2. Uso de la biblioteca SymPy para operaciones simbólicas

 >>> from sympy import * >>> init_printing(use_unicode=False,wrap_line=False,no_global=True) >>> p,u,d=symbols('pu d') >>> m2=p*u**2+(1-p)*d**2 >>> m1=p*u+(1-p)*d >>> v=m2-m1**2 >>> factor(v) 

La ecuación anterior responde a la siguiente pregunta: para una regla comercial dada caracterizada por los parámetros {π–, π +, n}, ¿cuál es el grado de precisión p necesario para lograr la relación de Sharpe igual a θ *? Por ejemplo, para obtener θ = 2 para n = 260, π– = –.01, π + = .005, necesitamos p = .72. Debido a la gran cantidad de apuestas, un cambio muy pequeño en p (de p = .7 a p = .72) promovió el coeficiente de Sharp de θ = 1.173 a θ = 2. Por otro lado, esto también nos dice que esta estrategia es vulnerable a pequeños cambios en p. El listado 15.3 implementa la derivación de la precisión esperada. En la fig. 15.2 muestra la supuesta precisión en función de n y π–, donde π + = 0.1 y θ * = 1.5. A medida que el umbral π– se vuelve más negativo para un n dado, se requiere un mayor grado p para lograr θ * para un umbral dado π +. A medida que el número n se hace más pequeño para un umbral dado π–, se requiere un mayor grado de p para lograr θ * para un π + dado.

Listado 15.3. Cálculo de precisión estimada

 def binHR(sl,pt,freq,tSR): ´´´ 

Para una regla comercial determinada caracterizada por los parámetros {sl, pt, freq}, ¿cuál es la precisión mínima requerida para lograr una relación de Sharpe igual a tSR?

1) entradas
sl: umbral de parada de pérdida
pt: umbral de beneficio
freq: el número de apuestas por año
tSR: índice promedio anual de Sharpe
2) Salir
p: precisión mínima p requerida para lograr tSR
´´´
a = (frecuencia + tSR ** 2) * (pt-sl) ** 2
b = (2 * frecuencia * sl-tSR ** 2 * (pt-sl)) * (pt-sl)
c = frecuencia * sl ** 2
p = (- b + (b ** 2-4 * a * c) **. 5) / (2. * a)
volver p


El listado 15.4 resuelve θ [p, n, π–, π +] para la frecuencia estimada de apuestas n. En la fig. 15.3 muestra la frecuencia estimada dependiendo de p y π–, donde π + = 0.1 y θ * = 1.5. A medida que el umbral π– se vuelve más negativo para un grado dado p, se requiere un número mayor n para lograr θ * para un umbral dado π +. A medida que el grado p se hace más pequeño para un umbral dado π–, se requiere un número mayor n para lograr θ * para un umbral dado π +.

Listado 15.4. Cálculo de la frecuencia estimada de apuestas

 def binFreq(sl,pt,p,tSR): ´´´ 

Para una regla comercial dada, caracterizada por los parámetros {sl, pt, freq}, ¿cuántas apuestas por año son necesarias para lograr el coeficiente Sharp tSR con un grado de precisión p?

Nota: ecuación con radicales, verificar soluciones extrañas.

1) entradas
sl: umbral de parada de pérdida
pt: umbral de beneficio
p: grado de precisión p
tSR: índice promedio anual de Sharpe
2) Salir
freq: la cantidad de apuestas necesarias por año
´´´
freq = (tSR * (pt-sl)) ** 2 * p * (1-p) / ((pt-sl) * p + sl) ** 2 # posiblemente extraño
si no np.isclose (binSR (sl, pt, freq, p), tSR): return
devolución de frecuencia



»Se puede encontrar más información sobre el libro en el sitio web del editor
» Contenidos
» Extracto

Cupón de 25% de descuento para vendedores ambulantes - Machine Learning

Tras el pago de la versión en papel del libro, se envía una versión electrónica del libro por correo electrónico.