
Este es un artículo de traducción del taller de Stanford . Pero ante ella hay una pequeña introducción. ¿Cómo se forman los zombies? Todos cayeron en una situación en la que quieres atraer a un amigo o colega a tu nivel, pero no funciona. Además, "no funciona" no tanto con usted como con él: en un lado de la balanza hay un salario normal, tareas, etc., y en el otro, la necesidad de pensar. Pensar es desagradable y doloroso. Rápidamente se da por vencido y continúa escribiendo código, completamente sin incluir el cerebro. Se imagina cuánto esfuerzo necesita gastar para superar la barrera de la impotencia aprendida, y simplemente no lo hace. Así es como se forman los zombies, que aparentemente se pueden curar, pero parece que nadie lo hará.
Cuando vi que Leslie Lampport (sí, esa misma amiga de los libros de texto) venía a Rusia y no daba un informe, sino una sesión de preguntas y respuestas, fui un poco cauteloso. Por si acaso, Leslie es un científico de fama mundial, autor de los trabajos fundamentales en informática distribuida, y también puede conocerlo por las letras La en LaTeX - "Lamport TeX". El segundo factor alarmante es su demanda: todos los que vengan deben (completamente gratis) escuchar con anticipación un par de sus informes, formular al menos una pregunta sobre ellos y solo entonces venir. Decidí ver qué transmitía Lampport allí, ¡y fue genial! Esto es exactamente eso, una píldora de enlace mágico para tratar a un zombie. Te advierto: del texto puede quemarse notablemente para los fanáticos de las metodologías súper flexibles y los no entusiastas para probar lo que está escrito.
Después de habrokat, de hecho, comienza la traducción del seminario. Que tengas una buena lectura!
Independientemente de la tarea que realice, siempre debe seguir tres pasos:
- decide qué objetivo quieres alcanzar;
- decide cómo lograrás tu objetivo;
- ven a tu meta.
Esto también se aplica a la programación. Cuando escribimos el código, necesitamos:
- decidir qué debe hacer el programa;
- determinar exactamente cómo debe cumplir su tarea;
- Escribe el código apropiado.
El último paso, por supuesto, es muy importante, pero hoy no hablaré sobre eso. En cambio, discutimos los dos primeros. Cada programador los realiza antes de comenzar a trabajar. No te sientas a escribir si no has decidido lo que estás escribiendo: un navegador o una base de datos. Una idea definitiva de la meta debe estar presente. Y está seguro de pensar en qué hará exactamente el programa, y no escribirlo de alguna manera con la esperanza de que el código se convierta de alguna manera en un navegador.
¿Cómo tiene lugar exactamente este pensamiento preliminar del código? ¿Cuánto esfuerzo deberíamos gastar en esto? Todo depende de cuán difícil sea el problema que estamos resolviendo. Supongamos que queremos escribir un sistema distribuido tolerante a fallas. En este caso, deberíamos considerar todo correctamente antes de sentarnos para el código. ¿Y si solo necesitamos aumentar la variable entera en 1? A primera vista, todo es trivial aquí, y no se necesitan pensamientos, pero luego recordamos que puede ocurrir un desbordamiento. Por lo tanto, incluso para comprender si un problema es simple o complejo, primero debe pensar.
Si piensa en las posibles soluciones al problema, puede evitar errores. Pero esto requiere que tu pensamiento sea claro. Para lograr esto, debe escribir sus pensamientos. Realmente me gusta la cita de Dick Gindon: "Cuando escribes, la naturaleza te muestra lo descuidado que es tu pensamiento". Si no escribes, solo te parece que piensas. Y necesita escribir sus pensamientos en forma de especificaciones.
Las especificaciones cumplen muchas funciones, especialmente en grandes proyectos. Pero solo hablaré de uno de ellos: nos ayudan a pensar con claridad. Pensar claramente es muy importante y bastante difícil, por lo que aquí necesitamos cualquier ayuda. ¿En qué idioma debemos escribir las especificaciones? Esta es siempre la primera pregunta para los programadores: en qué idioma escribiremos. No hay una respuesta correcta: los problemas que resolvemos son muy diversos. TLA + es útil para algunos: este es el lenguaje de especificación que desarrollé. Para otros, es más conveniente usar chino. Todo depende de la situación.
Otra pregunta es más importante: ¿cómo lograr un pensamiento más claro? Respuesta: debemos pensar como científicos. Esta es una forma de pensar que se ha demostrado en los últimos 500 años. En ciencia, construimos modelos matemáticos de la realidad. La astronomía fue quizás la primera ciencia en el sentido estricto de la palabra. En el modelo matemático utilizado en astronomía, los cuerpos celestes aparecen como puntos con masa, posición e impulso, aunque en realidad son objetos extremadamente complejos con montañas y océanos, mareas. Este modelo, como cualquier otro, está diseñado para resolver ciertos problemas. Es ideal para determinar dónde apuntar el telescopio, si necesita encontrar un planeta. Pero si quieres predecir el clima en este planeta, este modelo no funcionará.
Las matemáticas nos permiten determinar las propiedades de un modelo. Y la ciencia muestra cómo estas propiedades se relacionan con la realidad. Hablemos de nuestra ciencia, informática. La realidad con la que trabajamos son los sistemas informáticos de varios tipos: procesadores, consolas de juegos, computadoras, programas de ejecución, etc. Hablaré sobre ejecutar un programa en una computadora, pero en general, todas estas conclusiones se aplican a cualquier sistema informático. En nuestra ciencia, utilizamos muchos modelos diferentes: una máquina de Turing, conjuntos de eventos parcialmente ordenados y muchos otros.
¿Qué es un programa? Este es cualquier código que se pueda considerar de forma independiente. Supongamos que necesitamos escribir un navegador. Realizamos tres tareas: diseñamos la presentación del programa para el usuario, luego escribimos un esquema de alto nivel del programa y finalmente escribimos el código. A medida que escribimos el código, entendemos que necesitamos escribir una herramienta para formatear el texto. Aquí nuevamente necesitamos resolver tres problemas: determinar qué texto devolverá esta herramienta; elija un algoritmo para formatear; escribir código Esta tarea tiene su propia subtarea: insertar guiones en las palabras correctamente. También resolvemos esta subtarea en tres pasos: como vemos, se repiten en muchos niveles.
Consideremos con más detalle el primer paso: qué problema resuelve el programa. Aquí a menudo modelamos un programa como una función que recibe algo de entrada y da algo de salida. En matemáticas, una función generalmente se describe como un conjunto ordenado de pares. Por ejemplo, la función de cuadratura para números naturales se describe como el conjunto {<0,0>, <1,1>, <2,4>, <3,9>, ...}. El alcance de dicha función es el conjunto de los primeros elementos de cada par, es decir, los números naturales. Para definir una función, necesitamos especificar su alcance y fórmula.
Pero las funciones en matemáticas no son las mismas que las funciones en lenguajes de programación. Las matemáticas son mucho más simples. Como no tengo tiempo para ejemplos complejos, considere uno simple: una función en C o un método estático en Java que devuelve el divisor común más grande de dos enteros. En la especificación de este método, escribimos: calcula GCD(M,N) para los argumentos M y N , donde GCD(M,N) es una función cuyo dominio es el conjunto de pares de enteros, y el valor de retorno es el entero más grande que es divisible por M y N ¿Cómo se relaciona la realidad con este modelo? El modelo funciona con enteros, y en C o Java tenemos un int 32 bits. Este modelo nos permite decidir si el algoritmo GCD es correcto, pero no evitará errores de desbordamiento. Esto requeriría un modelo más complejo, para el cual no hay tiempo.
Hablemos de las limitaciones de la función como modelo. El trabajo de algunos programas (por ejemplo, sistemas operativos) no se reduce a devolver un cierto valor para ciertos argumentos; pueden ejecutarse continuamente. Además, la función como modelo no es adecuada para el segundo paso: planificar un método para resolver el problema. La clasificación rápida y la clasificación de burbujas calculan la misma función, pero estos son algoritmos completamente diferentes. Por lo tanto, para describir la forma de lograr el objetivo del programa, utilizo un modelo diferente, llamémoslo el modelo de comportamiento estándar. El programa en él se presenta como el conjunto de todos los comportamientos permitidos, cada uno de los cuales, a su vez, es una secuencia de estados, y un estado es una asignación de valores a variables.
Veamos cómo será el segundo paso para el algoritmo euclidiano. Necesitamos calcular GCD(M, N) . Inicializamos M como x , y N como y , luego volvemos a restar la más pequeña de estas variables de la más grande hasta que sean iguales. Por ejemplo, si M = 12 y N = 18 , podemos describir el siguiente comportamiento:
[x = 12, y = 18] → [x = 12, y = 6] → [x = 6, y = 6]
¿Y si M = 0 y N = 0 ? El cero es divisible por todos los números, por lo que no hay un divisor mayor en este caso. En esta situación, debemos volver al primer paso y preguntar: ¿realmente necesitamos calcular el MCD para números no positivos? Si esto no es necesario, solo necesita cambiar la especificación.
Aquí se debe hacer una pequeña digresión sobre la productividad. A menudo se mide por la cantidad de líneas de código escritas por día. Pero su trabajo es mucho más útil si se deshace de un cierto número de líneas, porque tiene menos espacio para errores. Y la forma más fácil de deshacerse del código es en el primer paso. Es posible que simplemente no necesite todas esas campanas y silbatos que está tratando de implementar. La forma más rápida de simplificar un programa y ahorrar tiempo es no hacer cosas que no valen la pena. El segundo paso está en segundo lugar en términos de potencial para ahorrar tiempo. Si mide la productividad por la cantidad de líneas escritas, pensar en cómo completar la tarea lo hará menos productivo , ya que puede resolver el mismo problema con menos código. No puedo proporcionar estadísticas exactas aquí, porque no tengo forma de calcular la cantidad de líneas que no escribí porque pasé tiempo en la especificación, es decir, en el primer y segundo paso. Y el experimento tampoco se puede poner aquí, porque en el experimento no tenemos derecho a completar el primer paso, la tarea está predeterminada.
En las especificaciones informales, muchas dificultades se pasan por alto fácilmente. No hay nada complicado en escribir especificaciones estrictas para las funciones; no discutiré esto. En cambio, hablaremos sobre cómo escribir especificaciones rigurosas para modelos de comportamiento estándar. Existe un teorema que establece que cualquier conjunto de comportamientos puede describirse utilizando la propiedad de seguridad y la propiedad de vida . La seguridad significa que no pasará nada malo, el programa no dará la respuesta incorrecta. La vitalidad significa que tarde o temprano sucederá algo bueno, es decir, el programa tarde o temprano dará la respuesta correcta. Como regla general, la seguridad es un indicador más importante; los errores suelen surgir aquí. Por lo tanto, para ahorrar tiempo, no hablaré sobre la supervivencia, aunque, por supuesto, también es importante.
Logramos seguridad prescribiendo, en primer lugar, los muchos estados iniciales posibles. Y en segundo lugar, las relaciones con todos los próximos estados posibles para cada estado. Nos comportaremos como científicos y definiremos los estados matemáticamente. El conjunto de estados iniciales se describe mediante la fórmula, por ejemplo, en el caso del algoritmo euclidiano: (x = M) ∧ (y = N) . Para ciertos valores de M y N solo hay un estado inicial. La relación con el siguiente estado se describe mediante una fórmula en la que las variables del siguiente estado se escriben con un guión y el estado actual sin guión. En el caso del algoritmo euclidiano, trataremos la disyunción de dos fórmulas, en una de las cuales x es el valor más grande, y en la segunda - y :
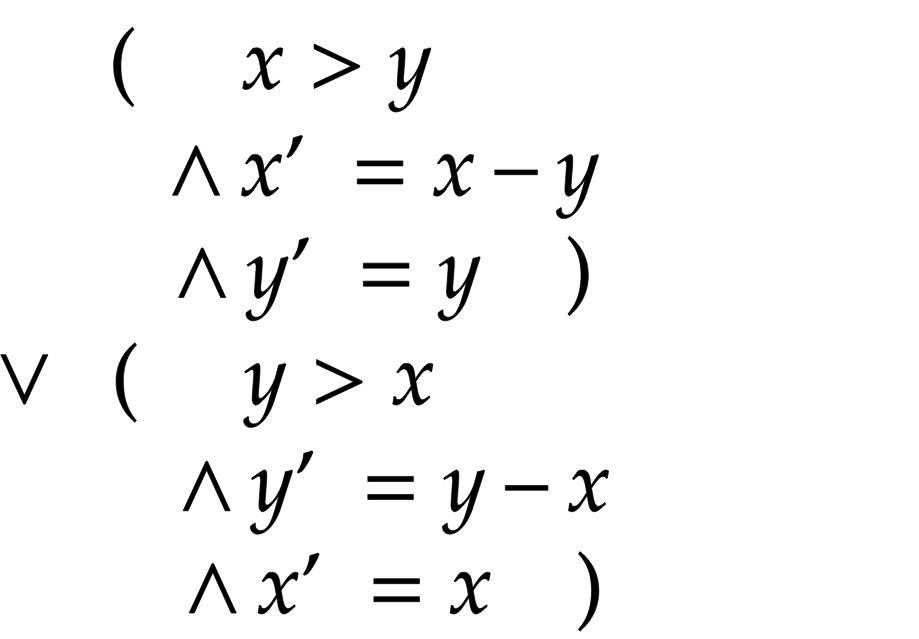
En el primer caso, el nuevo valor de y es igual al valor anterior de y, y obtenemos el nuevo valor de x, restando el más pequeño de la variable más grande. En el segundo caso, hacemos lo contrario.
Volvamos al algoritmo euclidiano. Supongamos nuevamente que M = 12 , N = 18 . Esto determina el único estado inicial, (x = 12) ∧ (y = 18) . Luego sustituimos estos valores en la fórmula anterior y obtenemos:

Aquí la única solución posible: x' = 18 - 12 ∧ y' = 12 , y obtenemos el comportamiento: [x = 12, y = 18] . Del mismo modo, podemos describir todos los estados en nuestro comportamiento: [x = 12, y = 18] → [x = 12, y = 6] → [x = 6, y = 6] .
En el último estado [x = 6, y = 6] ambas partes de la expresión serán falsas, por lo tanto, no tiene el siguiente estado. Entonces, tenemos la especificación completa del segundo paso: como vemos, esta es una matemática bastante común, como la de los ingenieros y científicos, y no extraña, como en la informática.
Estas dos fórmulas se pueden combinar en una fórmula lógica temporal. Es elegante y fácil de explicar, pero ahora no tiene tiempo. La lógica temporal puede que solo necesitemos para la propiedad de vivacidad, por seguridad no es necesaria. La lógica temporal como tal no es agradable, no es matemática del todo ordinaria, pero en el caso de la vivacidad es un mal necesario.
En el algoritmo euclidiano, para cada valor de x e y hay valores únicos de x' e y' que hacen que la relación con el siguiente estado sea verdadera. En otras palabras, el algoritmo euclidiano es determinista. Para simular un algoritmo no determinista, es necesario que el estado actual tenga varios estados futuros posibles, y que cada valor de la variable sin primo tenga varios valores de la variable con un trazo en el que la relación con el siguiente estado sea verdadera. Esto no es difícil de hacer, pero no daré ejemplos ahora.
Para hacer una herramienta de trabajo, necesitas matemática formal. ¿Cómo hacer que la especificación sea formal? Para hacer esto, necesitamos un lenguaje formal, por ejemplo, TLA + . La especificación del algoritmo euclidiano en este lenguaje se verá así:

El símbolo de signo igual con un triángulo significa que el valor a la izquierda del signo se define como igual al valor a la derecha del signo. En esencia, una especificación es una definición, en nuestro caso dos definiciones. Debe agregar declaraciones y alguna sintaxis a la especificación en TLA +, como en la diapositiva anterior. En ASCII, se verá así:

Como puedes ver, nada complicado. La especificación para TLA + se puede verificar, es decir, omitir todos los comportamientos posibles en un modelo pequeño. En nuestro caso, este modelo tendrá ciertos valores de M y N Este es un método de verificación muy eficiente y fácil que se ejecuta de forma completamente automática. Además, puede escribir pruebas formales de la verdad y verificarlas mecánicamente, pero esto lleva mucho tiempo, por lo que casi nadie lo hace.
La principal desventaja de TLA + es que es matemática, y los programadores y los informáticos tienen miedo de las matemáticas. A primera vista, esto suena como una broma, pero, desafortunadamente, lo digo con toda seriedad. Mi colega me contó cómo intentó explicar TLA + a varios desarrolladores. Tan pronto como las fórmulas aparecieron en la pantalla, inmediatamente tuvieron ojos de cristal. Entonces, si TLA + da miedo, puede usar PlusCal , es una especie de lenguaje de programación de juguetes. Una expresión en PlusCal puede ser cualquier expresión TLA +, es decir, en general, cualquier expresión matemática. PlusCal también tiene sintaxis para algoritmos no deterministas. Debido al hecho de que cualquier expresión TLA + se puede escribir en PlusCal, es mucho más expresivo de cualquier lenguaje de programación real. PlusCal se compila aún más en la especificación TLA + fácil de leer. Esto no significa, por supuesto, que la compleja especificación PlusCal se convertirá en una simple en TLA +: solo la correspondencia entre ellos es obvia, no habrá complejidad adicional. Finalmente, esta especificación se puede verificar con las herramientas TLA +. En general, PlusCal puede ayudar a superar la fobia de las matemáticas; es fácil de entender incluso para programadores y científicos informáticos. En el pasado, durante algún tiempo (unos 10 años), publiqué algoritmos sobre él.
Quizás alguien objetará que TLA + y PlusCal son matemáticas, y las matemáticas solo funcionan en ejemplos inventados. En la práctica, necesita un lenguaje real con tipos, procedimientos, objetos, etc. Esto no es asi. Esto es lo que escribe Chris Newcomb, que trabajó en Amazon: “Utilizamos TLA + en diez proyectos grandes, y en cada caso, su uso hizo una contribución significativa al desarrollo, porque pudimos detectar errores peligrosos antes de entrar en producción, y porque nos dio comprensión y confianza necesarias para optimizaciones de rendimiento agresivas que no afectan la verdad del programa " . A menudo se puede escuchar que cuando usamos métodos formales, obtenemos un código ineficiente; en la práctica, todo es exactamente lo contrario. Además, se cree que los gerentes no pueden estar convencidos de la necesidad de métodos formales, incluso si los programadores están convencidos de su utilidad. Y Newcomb escribe: "Los gerentes ahora están presionando en todos los sentidos para escribir especificaciones para TLA +, y específicamente dedican tiempo a esto" . Entonces, cuando los gerentes ven que TLA + está funcionando, están felices de aceptarlo. Chris Newcomb escribió esto hace unos seis meses (en octubre de 2014), pero ahora, hasta donde yo sé, TLA + se usa en 14 proyectos, no en 10. Otro ejemplo se relaciona con el diseño de la XBox 360. Un pasante vino a Charles Thacker y escribió especificación para un sistema de memoria. Gracias a esta especificación, se encontró un error que de otro modo no se habría notado, y por lo que cada XBox 360 se caería después de cuatro horas de uso. Los ingenieros de IBM han confirmado que sus pruebas no habrían detectado este error.
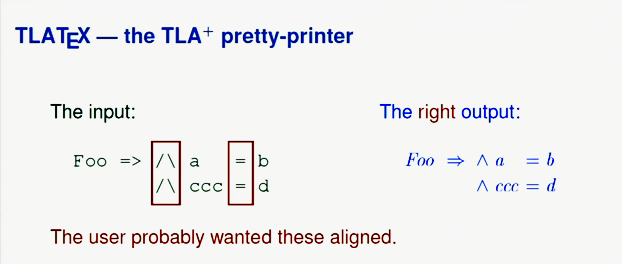
Puede leer más sobre TLA + en Internet y ahora hablemos sobre especificaciones informales. Raramente tenemos que escribir programas que calculen el divisor menos común y similares. Más a menudo, escribimos programas como la herramienta de impresora bonita que escribí para TLA +. Después del procesamiento más simple, el código TLA + se vería así:

Pero en el ejemplo anterior, el usuario probablemente quería que la conjunción y los signos de igualdad estuvieran alineados. Entonces el formato correcto se vería más así:
Considere otro ejemplo:

Aquí, por el contrario, la alineación de signos iguales, suma y multiplicación en la fuente fue aleatoria, por lo que el procesamiento más simple es suficiente. En general, no existe una definición matemática exacta del formato correcto, porque "correcto" en este caso significa "lo que el usuario quiere", y esto no puede determinarse matemáticamente.
Parecería que si no tenemos una definición de verdad, entonces la especificación es inútil. Pero esto no es así. Si no sabemos exactamente qué debe hacer el programa, esto no significa que no necesitemos pensar en su trabajo; por el contrario, deberíamos invertir aún más esfuerzo en esto. La especificación aquí es especialmente importante. Es imposible determinar el programa óptimo para el listado estructural, pero esto no significa que no debamos emprenderlo en absoluto, y escribir código como una corriente de conciencia no es una cosa. Al final, escribí una especificación de seis reglas con definiciones en forma de comentarios en un archivo Java. Aquí hay un ejemplo de una de las reglas: a left-comment token is LeftComment aligned with its covering token . Esta regla está escrita, por ejemplo, en inglés matemático: LeftComment aligned , left-comment y el covering token son términos con definiciones. Así es como los matemáticos describen las matemáticas: escriben definiciones de términos y, sobre la base de ellos, reglas. El beneficio de esta especificación es que comprender y depurar las seis reglas es mucho más simple que 850 líneas de código. Debo decir que escribir estas reglas no fue fácil, se dedicó mucho tiempo a depurarlas. Especialmente para este propósito, escribí un código que informaba qué regla se usaba. Debido al hecho de que verifiqué estas seis reglas con algunos ejemplos, no necesité depurar 850 líneas de código, y los errores resultaron ser bastante fáciles de encontrar. Java tiene algunas herramientas excelentes para esto. Si solo escribiera el código, me llevaría mucho más tiempo y el formato resultaría ser de peor calidad.
¿Por qué era imposible usar una especificación formal? Por un lado, la ejecución correcta no es muy importante aquí. Una lista estructural seguramente no complacerá a nadie, por lo que no necesitaba obtener el trabajo adecuado en todas las situaciones inusuales. Aún más importante es el hecho de que no tenía las herramientas adecuadas. La herramienta para probar modelos TLA + es inútil aquí, por lo que tendría que escribir ejemplos manualmente.
La especificación dada tiene características comunes a todas las especificaciones. Es de un nivel más alto que el código. Puede implementarlo en cualquier idioma. Para escribirlo, cualquier herramienta o método es inútil. Ningún curso de programación te ayudará a escribir esta especificación. Y no hay herramientas que puedan hacer que esta especificación sea innecesaria a menos que, por supuesto, escriba un lenguaje específicamente para escribir programas de listado estructural en TLA +. Finalmente, esta especificación no dice nada sobre exactamente cómo escribiremos el código, solo indica lo que hace este código. Estamos escribiendo una especificación para ayudarnos a pensar en el problema antes de comenzar a pensar en el código.
Pero esta especificación también tiene características que la distinguen de otras especificaciones. El 95% de otras especificaciones son mucho más cortas y simples:

Además, esta especificación es un conjunto de reglas. Esto suele ser un signo de mala especificación. Comprender las implicaciones del conjunto de reglas es bastante difícil, por eso tuve que pasar mucho tiempo depurándolas. Sin embargo, en este caso no pude encontrar una mejor manera.
Vale la pena decir algunas palabras sobre los programas que funcionan continuamente. Como regla, funcionan en paralelo, por ejemplo, sistemas operativos o sistemas distribuidos. Muy pocos pueden entenderlos en sus mentes o en papel, y yo no soy uno de ellos, aunque una vez me lo podía permitir. Por lo tanto, se necesitan herramientas que prueben nuestro trabajo, por ejemplo, TLA + o PlusCal.
¿Por qué necesitabas escribir una especificación si ya sabía qué debía hacer exactamente el código? De hecho, solo me pareció que lo sabía. Además, si hay una especificación, un extraño ya no necesita ingresar al código para comprender exactamente qué está haciendo. Tengo una regla: no debería haber ninguna regla general. Esta regla, por supuesto, tiene una excepción, esta es la única regla general que sigo: la especificación de lo que hace el código debería decirle a las personas todo lo que necesitan saber al usar este código.
Entonces, ¿qué deben saber exactamente los programadores sobre el pensamiento? Para empezar, lo mismo que todos: si no escribes, solo piensas que piensas. Además, debe pensar antes de codificar, lo que significa que debe escribir antes de codificar. Una especificación es lo que escribimos antes de comenzar a codificar. La especificación es necesaria para cualquier código que cualquiera pueda usar o modificar. Y este "alguien" puede llegar a ser el autor del código un mes después de haberlo escrito. La especificación es necesaria para programas y sistemas grandes, para clases, para métodos y, a veces, incluso para secciones complejas de un solo método. ¿Qué se debe escribir exactamente sobre el código? Es necesario describir lo que está haciendo, es decir, algo que puede ser útil para cualquier persona que use este código. A veces también puede ser necesario indicar exactamente cómo el código logra su objetivo. Si pasamos este método en el curso de algoritmos, entonces lo llamamos algoritmo. Si es algo más especial y nuevo, entonces lo llamamos diseño de alto nivel. No hay diferencia formal: ambos son un modelo abstracto del programa.
¿Cómo exactamente se debe escribir una especificación de código? Lo principal: debe ser un nivel más alto que el código en sí. Debe describir estados y comportamientos. Debe ser tan estricto como lo requiera la tarea. Si está escribiendo una especificación de cómo implementar la tarea, puede escribirse en pseudocódigo o usando PlusCal. Aprender a escribir especificaciones es necesario en especificaciones formales. Esto le dará las habilidades necesarias que ayudarán, incluso a aquellos con habilidades informales. ¿Y cómo aprender a escribir especificaciones formales? Cuando aprendimos programación, escribimos programas y luego los depuramos.Lo mismo aquí: debe escribir una especificación, verificarla con la herramienta de verificación de modelos y corregir los errores. TLA + puede no ser el mejor idioma para una especificación formal, y otro idioma probablemente sería mejor para sus necesidades específicas. La ventaja de TLA + es que te enseña un gran pensamiento matemático.
¿Cómo vincular la especificación y el código? Con la ayuda de comentarios que conectan conceptos matemáticos y su implementación. Si trabaja con gráficos, en el nivel del programa tendrá conjuntos de nodos y conjuntos de enlaces. Por lo tanto, debe escribir exactamente cómo se implementa el gráfico mediante estas estructuras de programación.
, . , , . , . . , , . , . , .
— . — Amazon. . ? . , , . , . — , . . .
. - , , . , - , , . . , . , , . , ? -, , , , . , . , . , , . -, , . . , , .
, , . - . , — . , , . , , , , . . , . , , — . , .
TLA+ PlusCal , . , .
, . — , . , Hydra 2019, 11-12 2019 -. .