
Desde su lanzamiento en agosto de 2018, Julia ha ganado popularidad activamente al ingresar a los 10 idiomas principales en Github y las 20 habilidades profesionales más populares según Upwork . Para principiantes, comienzan los cursos y se publican libros . Julia se utiliza para la planificación de misiones espaciales , farmacometría y modelación climática .
Antes de proceder a la computación distribuida en Julia, pasemos a la experiencia de aquellos que ya han probado esta oportunidad de un nuevo PL para problemas aplicados, desde la ecuación de difusión en dos núcleos, hasta mapas astronómicos en una supercomputadora.
Computación paralela y factores que afectan el rendimiento de la computación paralela
La mayoría de las computadoras modernas tienen más de un procesador, y varias computadoras se pueden combinar en un clúster. El uso de la potencia de múltiples procesadores le permite realizar muchos cálculos más rápido. El rendimiento se ve afectado por dos factores principales: la velocidad de los procesadores mismos y la velocidad de acceso a su memoria. En un clúster, esta CPU tendrá el acceso más rápido a la RAM ubicada en la misma computadora o host. Aún más sorprendente, estos problemas son relevantes en una computadora portátil multi-core típica debido a las diferencias en la velocidad de la memoria principal y la memoria caché. Por lo tanto, un buen entorno multiprocesador debería permitirle controlar el uso de parte de la memoria por un procesador específico.
Computación Paralela en Julia
Julia tiene varias primitivas incorporadas para la computación paralela en cada nivel: vectorización (SIMD), multihilo y computación distribuida.
El propio subprocesamiento múltiple de Julia le permite al usuario usar las capacidades de una computadora portátil multinúcleo, mientras que las primitivas de llamada remota y acceso remoto le permiten distribuir el trabajo entre muchos procesos en el clúster. Además de estas primitivas integradas, varios paquetes en el ecosistema de Julia proporcionan un procesamiento paralelo eficiente.
Vectorización automática en Julia
Los chips Intel modernos proporcionan una serie de extensiones de conjunto de comandos. Entre ellos se encuentran varias versiones de Streaming SIMD Extension (SSE) y varias generaciones de extensiones vectoriales (disponibles en las últimas familias de procesadores). Estas extensiones proporcionan programación en el estilo de Datos múltiples de instrucción única (SIMD) , proporcionando una aceleración significativa para el código que se presta a dicho estilo de programación. El potente compilador Julia de LLia puede generar automáticamente códigos de máquina altamente eficientes para funciones básicas y definidas por el usuario en cualquier arquitectura, como SIMD Hardware (compatible con LLVM ), que le permite al usuario preocuparse menos por escribir código especializado para cada una de estas arquitecturas. Otra ventaja de usar el compilador para mejorar el rendimiento, en lugar de codificar manualmente los "bucles activos" en un ensamblaje, es que es significativamente mejor para el futuro. Cada vez que sale la arquitectura del conjunto de instrucciones de próxima generación, el código personalizado de Julia se vuelve más rápido automáticamente.
Multithreading
Multithreading en Julia generalmente toma la forma de bucles paralelos. También hay primitivas para bloqueos y atómicos que permiten a los usuarios sincronizar su código. Las primitivas paralelas de Julia son simples pero poderosas. Se muestra que escalan a miles de nodos y procesan terabytes de datos .
Computación distribuida
Aunque las primitivas incorporadas de Julia son suficientes para implementaciones paralelas a gran escala, hay una serie de paquetes para un trabajo más especializado. ClusterManagers.jl proporciona interfaces para una serie de sistemas de colas de trabajos comúnmente utilizados en clústeres informáticos, como Sun Grid Engine y Slurm . DistributedArrays.jl proporciona una interfaz conveniente para las matrices de datos distribuidas en un clúster. Esto combina los recursos de memoria de varias máquinas, lo que hace posible el uso de matrices que son demasiado grandes para caber en una máquina. Cada proceso se ejecuta por parte de la matriz que posee, proporcionando una respuesta preparada a la pregunta de cómo se debe dividir el programa entre máquinas.
En algunas aplicaciones heredadas, los usuarios prefieren no repensar su modelo paralelo y desean seguir usando simultaneidad al estilo MPI . Para ellos, MPI.jl proporciona una envoltura delgada alrededor de MPI que permite a los usuarios utilizar procedimientos de paso de mensajes al estilo MPI.
Julia en batalla
El Proyecto Celeste es una colaboración entre Julia Computing, Intel Labs, JuliaLabs @ MIT, Lawrence Berkeley National Labs y la Universidad de California en Berkeley.
Celeste es un modelo jerárquico totalmente generativo que utiliza inferencia estadística para determinar matemáticamente la ubicación y las características de las fuentes de luz en el cielo. Este modelo permite a los astrónomos identificar galaxias prometedoras para dirigir espectrógrafos y ayuda a comprender el papel de la energía oscura, la materia oscura y la geometría del universo.

Ejemplo de Sloan Digital Sky Survey (SDSS)
Utilizando las capacidades informáticas paralelas de Julia, el equipo de investigación de Celeste procesó 55 terabytes de datos visuales y clasificó 188 millones de objetos astronómicos en solo 15 minutos, lo que resultó en el primer catálogo completo de todos los objetos visibles de Sloan Digital Sky Survey . Este es uno de los mayores problemas de optimización matemática que la humanidad haya resuelto.

El proyecto Celeste utilizó 9,300 nodos de Knights Landing (KNL) en la supercomputadora NERSC Cori Phase II para ejecutar 1.3 millones de hilos en 650,000 núcleos KNL, que combinaron la lista de aplicaciones con velocidades superiores a 1 petaflops por segundo , haciendo de Julia la única dinámica un lenguaje de alto nivel que alguna vez ha logrado tal hazaña. ?? Pero, ¿la sincronización de telescopios y el procesamiento de datos para una imagen de agujero negro en 10.04.19 rompió este récord? Parece que Python se usó principalmente allí.
Programación paralela con Julia usando MPI
Traducción de material del blog de física de plasma Claudio 2018-09-30
Julia ha existido desde 2012, y después de más de seis años de desarrollo, la versión 1.0 finalmente se lanzó. Esta es una etapa importante que me inspiró a crear una nueva publicación (después de varios meses de silencio). Esta vez veremos cómo hacer programación paralela en Julia usando el paradigma de interfaz de paso de mensajes (MPI) a través de la biblioteca de código abierto Open MPI. Haremos esto resolviendo un problema físico real: difusión de calor a través de una región bidimensional.

Figura 1. Supercomputadora Sequoia en LLNL con casi 1.6 millones de procesadores disponibles para la simulación numérica de armas nucleares. hpc.llnl.gov
Esta será una aplicación MPI bastante avanzada, dirigida a aquellos que ya tienen cierta comprensión de la computación paralela. Debido a esto, no voy a ir paso a paso, sino a centrarme en aspectos específicos que, en mi opinión, son de interés (en particular, el uso de células fantasmas y la transmisión de mensajes en una cuadrícula bidimensional). Siguiendo la tradición de sus publicaciones recientes, el código discutido aquí se presentará solo parcialmente. Esto va acompañado de una solución con todas las funciones que puede encontrar en Github: Diffusion.jl .
La computación paralela ha entrado en el "mundo comercial" en los últimos años. Esta es una solución estándar para aplicaciones ETL (Extraer-Transformar-Cargar), donde el problema en consideración es vergonzosamente paralelo: cada proceso se realiza independientemente de todos los demás, y no se requiere conexión de red (hasta que ocurra el paso final de "reducción", donde cada solución local se ensambla en solución global).
En muchas aplicaciones científicas, es necesario transmitir información a través de una red de clúster. Estos problemas de "compresión paralela" a menudo son simulaciones numéricas: problemas de astrofísica, modelación del clima, biología, sistemas cuánticos, etc. En algunos casos, estas simulaciones se realizan en docenas e incluso millones de procesadores (Fig. 1), y la memoria se distribuye entre diferentes procesadores. Por lo general, estos procesadores interactúan en una supercomputadora a través del paradigma de la interfaz de paso de mensajes (MPI).
Cualquiera que trabaje en informática de alto rendimiento debe estar familiarizado con MPI. Permite el uso de la arquitectura de clúster en un nivel muy bajo. Teóricamente, un investigador puede asignar a cada CPU su propia carga informática. Él / ella puede decidir exactamente cuándo y qué información se debe transferir entre los procesadores, y si esto debería ocurrir de forma síncrona o asíncrona.
Y ahora volvamos al contenido de esta publicación, donde veremos cómo escribir una solución para una ecuación de tipo de difusión usando MPI. Ya hemos discutido un esquema explícito para una ecuación unidimensional de este tipo ( Por cierto, también discutimos esto ). Sin embargo, en esta publicación consideraremos una solución bidimensional.
El código de Julia presentado aquí es esencialmente una traducción del código C / Fortran explicado en esa magnífica publicación de Fabien Durnak.
En esta publicación no analizaré en detalle la velocidad de escala y la cantidad de procesadores. Principalmente porque solo tengo dos procesadores con los que puedo jugar en casa (procesador Intel Core i7 en mi MacBook Pro) ... Sin embargo, todavía puedo decir con orgullo que el código de Julia presentado en esta publicación, muestra una aceleración significativa cuando se usan dos procesadores contra uno. De todos modos: ¡ es más rápido que los códigos Fortran y C equivalentes! (más sobre esto más adelante)
Estos son los temas que vamos a cubrir en esta publicación:
- Julia: mis primeras impresiones
- Cómo instalar Open MPI en tu computadora
- Problema: propagación a través de un dominio bidimensional
- Comunicación entre procesadores: la necesidad de células fantasmas
- Usando MPI
- Visualización de la solución
- Rendimiento
- Conclusiones
1. Primeras impresiones de Julia
De hecho, conocí a Julia recientemente, así que decidí centrarme en un par de "primeras impresiones" aquí.
La razón principal por la que me interesé en Julia es que promete ser un marco de uso general con un rendimiento comparable a C y Fortran , al tiempo que conserva la flexibilidad y la facilidad de uso de los lenguajes de script como Matlab o Python . De hecho, Julia debería poder escribir aplicaciones de Data Science / High-Performance-Computing que se ejecuten en la computadora local, en la nube o en supercomputadoras corporativas.
Un aspecto que no me gusta es el flujo de trabajo, que parece subóptimo para aquellos que, como yo, usan IntelliJ y PyCharm a diario (el complemento IntelliJ Julia es terrible). También probé el Juno IDE , que es probablemente la mejor solución en este momento, pero todavía necesito acostumbrarme.
Un aspecto que demuestra cómo Julia aún no ha alcanzado su "madurez" es lo variada y desactualizada que es la documentación de muchos paquetes ( para los paquetes que se han mantenido a flote, todo se ha abatido desde el año pasado ). Todavía no he encontrado una manera de escribir una matriz de números de punto flotante en el disco en forma formateada ( ahora es fácil de encontrar ). Por supuesto, puede escribir en el disco cada elemento de la matriz en un bucle doble, pero deberían estar disponibles mejores soluciones. Es solo que esta información es difícil de encontrar, y la documentación debe ser completa.
Otro aspecto que se destaca la primera vez que se usa Julia es la opción de usar la indexación de uno para las matrices. Aunque me parece un poco molesto desde un punto de vista práctico, ciertamente no rompe el acuerdo, dado que no es exclusivo de Julia (Matlab y Fortran también usan indexación comenzando con uno).
Ahora, al aspecto bueno y más importante: Julia realmente puede ser muy rápida. Me impresionó ver cómo el código de Julia que escribí para esta publicación puede funcionar mejor que el código Fortran y C equivalente, aunque básicamente lo traduje a Julia. Echa un vistazo a la sección de rendimiento si estás interesado.
2. Instalación de Open MPI
Open MPI es una biblioteca de interfaz de mensajería de código abierto. Otras bibliotecas conocidas incluyen MPICH y MVAPICH. Desarrollado por la Universidad Estatal de Ohio, MVAPICH es actualmente la biblioteca más avanzada porque también puede admitir clústeres de GPU, lo que es especialmente útil para aplicaciones de Aprendizaje profundo (de hecho, existe una estrecha colaboración entre NVIDIA y el equipo MVAPICH).
Todas estas bibliotecas están construidas en una interfaz común: API MPI. Por lo tanto, no importa si usa una u otra biblioteca: el código que escribió puede permanecer igual.
El proyecto MPI.jl en Github es un contenedor para MPI. Debajo del capó, utiliza instalaciones C y Fortran MPI. Funciona muy bien, aunque carece de algunas de las funciones disponibles en estos otros idiomas.
Para ejecutar MPI en Julia, necesitará instalar Open MPI por separado en su computadora. Si tienes una Mac, esta guía me pareció muy útil. Es importante tener en cuenta que también necesitará instalar gcc (el compilador GNU) ya que Open MPI requiere los compiladores Fortran y C. Instalé la versión de Open MPI 3.1.1, que también es confirmada por mpiexec --version en mi terminal.
Después de instalar Open MPI en su computadora, debe instalar cmake . Nuevamente, si tiene una Mac, es tan fácil como escribir brew install cmake en su terminal.
En este momento, está listo para instalar el paquete MPI en Julia. Abra Julia REPL y escriba using Pkg Pkg.add («MPI») . Por lo general, en este punto, debería poder importar el paquete usando MPI para importar. Sin embargo, también tuve que compilar el paquete a través de Pkg.build («MPI») antes de que funcionara.
3. Problema: ecuación de difusión bidimensional
La ecuación de difusión es un ejemplo de una ecuación diferencial parcial parabólica. Describe fenómenos como la difusión del calor o la difusión de la concentración (segunda ley de Fick). En dos dimensiones espaciales, se escribe la ecuación de difusión.
Solución muestra cómo cambia la temperatura / concentración (dependiendo de si estudiamos la distribución del calor o la difusión de sustancias) en el espacio y el tiempo. De hecho, las variables x e y representan las coordenadas espaciales, y el componente de tiempo está representado por la variable t . La cantidad D es el "coeficiente de difusión" y determina qué tan rápido, por ejemplo, el calor se propagará a través de la región física. Similar a lo que se discutió (en más detalle) en una publicación de blog anterior, la ecuación anterior se puede discretizar utilizando el llamado "esquema explícito" de la solución. No entraré en los detalles que puede encontrar en el blog, simplemente escriba una solución numérica en el siguiente formulario:
donde i y k índices que se ejecutan a lo largo de la cuadrícula espacial, j en el tiempo. La primera capa de tiempo se llena desde las condiciones iniciales, y cada una de las siguientes calculado utilizando los valores de la capa anterior. En la figura, los nodos rojos indican los nodos de la capa que son necesarios para calcular el valor en el punto

La ecuación (1) es realmente todo lo que se necesita para encontrar una solución en toda el área en cada paso de tiempo posterior. Es bastante simple implementar código que haga esto secuencialmente con un proceso en la CPU. Sin embargo, aquí queremos discutir una implementación paralela que utiliza varios procesos.
Cada proceso será responsable de encontrar una solución en parte de todo el dominio espacial. Los problemas como la difusión del calor, que no son candidatos claros para la computación distribuida, requieren el intercambio de información entre procesos. Para aclarar este punto, veamos la imagen
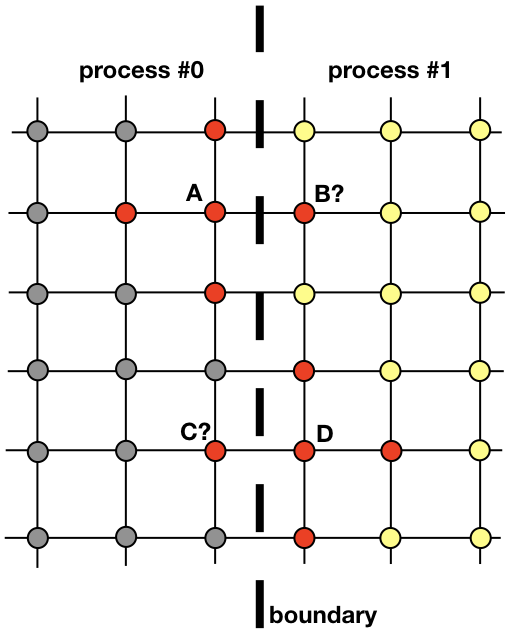
Dos procesos vecinos deben interactuar para encontrar una solución cerca de la frontera. El proceso 0 debe conocer el valor de la solución en B para calcular la solución en el punto de rejilla A. De manera similar, el proceso 1 debe conocer el valor en el punto C para calcular la solución en el punto de rejilla D. Estos valores son desconocidos para los procesos hasta que haya una conexión entre los procesos 0 y 1 .
Muestra cómo los procesos 0 y 1 deberán interactuar para evaluar una solución cerca del límite. Aquí es donde MPI entra en escena. En la siguiente sección, veremos una forma efectiva de mensajería.
4. Comunicación entre procesos: células fantasmas
Un concepto importante en la dinámica de fluidos computacional es el concepto de células fantasmas. Este concepto es útil siempre que un dominio espacial se descompone en varios subdominios, cada uno de los cuales se resuelve mediante un solo proceso.
Para comprender qué son las células fantasmas, veamos nuevamente dos áreas vecinas en la imagen anterior. El proceso 0 es responsable de encontrar la solución en el lado izquierdo, mientras que el proceso 1 la encuentra en el lado derecho del dominio espacial. Sin embargo, debido a la forma de la plantilla (Fig. 2) cerca del borde, ambos procesos tendrán que intercambiar datos entre sí. Aquí está el problema: es muy ineficiente que el proceso 0 y el proceso 1 se comuniquen cada vez que necesitan un nodo de un proceso vecino: esto generaría costos de comunicación inaceptables.
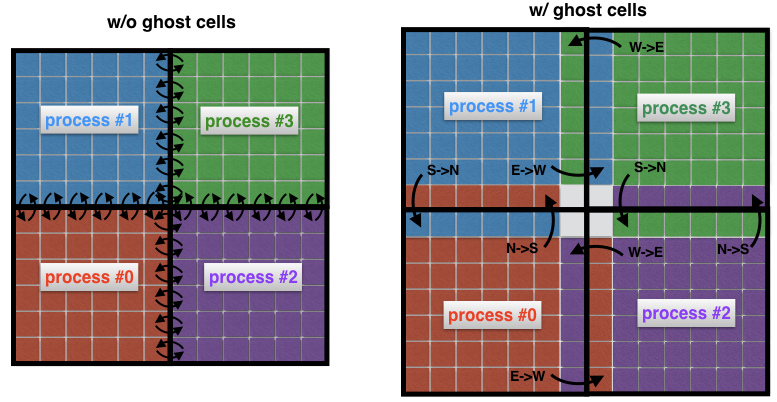
Fig. 4 Conexión entre procesos sin (fantasma) y con (fantasma) células fantasma. Sin celdas intermedias, cada celda en el borde de un subdominio debe transmitir su propio mensaje a un proceso vecino. El uso de celdas fantasmas le permite minimizar la cantidad de mensajes transmitidos, ya que muchas celdas que pertenecen a los límites del proceso intercambian un mensaje a la vez. Aquí, por ejemplo, el proceso 0 transfiere todo el límite norte al proceso 1, y todo el límite este al proceso 2.
En cambio, es una práctica común rodear los subdominios "reales" con celdas adicionales llamadas celdas fantasmas, como se muestra en la Figura 4 (derecha). Estas celdas fantasmas son copias de la solución en los bordes de los subdominios vecinos. En cada paso de tiempo, el límite anterior de cada subdominio se pasa a los vecinos. Esto le permite calcular una nueva solución en el borde de un subdominio con una sobrecarga de comunicación significativamente reducida. El efecto neto es la aceleración del código.
5. Usando MPI
Hay muchos tutoriales de MPI. Aquí solo quiero describir los comandos expresados en el lenguaje de shell MPI.jl para Julia que utilicé para resolver el problema de difusión bidimensional. Estos son algunos comandos básicos que se utilizan en casi todas las implementaciones de MPI.
Comandos MPIMPI.init () - inicializa el tiempo de ejecución
MPI.COMM_WORLD : representa el comunicador, es decir, todos los procesos disponibles a través de la aplicación MPI (cada mensaje debe estar asociado con el comunicador)
MPI.Comm_rank (MPI. COMM_WORLD) : define el rango interno (id) del proceso
MPI.Barrier (MPI.COMM_WORLD) : bloquea la ejecución hasta que todos los procesos hayan alcanzado este procedimiento
MPI.Bcast! (Buf, n_buf, rank_root, MPI.COMM_WORLD) MPI.Bcast! (Buf, n_buf, rank_root, MPI.COMM_WORLD) - transmite mensajes buffer buf con tamaño n_buf desde un proceso con rank rank_root a todos los demás procesos en el comunicador MPI.COMM_WORLD
MPI.Waitall! (reqs) MPI.Waitall! (reqs) : espera la finalización de todas las solicitudes MPI (la solicitud es un descriptor, en otras palabras, un enlace, para la transferencia de mensajes asíncronos)
MPI.REQUEST_NULL : indica que la solicitud no está asociada con ninguna conexión en curso
MPI.Gather (buf, rank_root, MPI.COMM_WORLD) : reduce la variable buf al proceso de obtención de rank_root
MPI.Isend (buf, rank_dest, tag, MPI.COMM_WORL D) : el mensaje buf se envía de forma asíncrona desde el proceso actual al proceso rank_dest, y el mensaje se etiqueta con el parámetro
MPI.Irecv! (Buf, rank_src, tag, MPI.COMM_WORLD) MPI.Irecv! (Buf, rank_src, tag, MPI.COMM_WORLD) : recibe un mensaje con la etiqueta de etiqueta desde el proceso de origen de rank rank_src hasta el almacenamiento intermedio local
MPI.Finalize () - finaliza el tiempo de ejecución de MPI
5.1 Proceso de búsqueda de vecinos
Para nuestra tarea, vamos a descomponer nuestra región bidimensional en muchos subdominios rectangulares, como se muestra en la figura a continuación.

Figura 5. Descomposición cartesiana de una región bidimensional dividida en 12 subdominios. Tenga en cuenta que los rangos MPI (identificadores de proceso) comienzan desde cero.
Tenga en cuenta que los ejes x e y están invertidos en relación con el uso normal para asociar el eje x con filas y el eje y con columnas de la matriz de solución.
Para comunicarse entre diferentes procesos, cada proceso debe conocer a sus vecinos. Hay un comando MPI muy útil que hace esto automáticamente y se llama MPI_Cart_create . Desafortunadamente, el shell Julia MPI no incluye este comando avanzado (y agregarlo no parece trivial), por lo que decidí crear una función que realice la misma tarea. Para hacerlo más compacto, a menudo utilicé el operador ternario . Puede encontrar esta función a continuación.
Código function neighbors(my_id::Int, nproc::Int, nx_domains::Int, ny_domains::Int) id_pos = Array{Int,2}(undef, nx_domains, ny_domains) for id = 0:nproc-1 n_row = (id+1) % nx_domains > 0 ? (id+1) % nx_domains : nx_domains n_col = ceil(Int, (id + 1) / nx_domains) if (id == my_id) global my_row = n_row global my_col = n_col end id_pos[n_row, n_col] = id end neighbor_N = my_row + 1 <= nx_domains ? my_row + 1 : -1 neighbor_S = my_row - 1 > 0 ? my_row - 1 : -1 neighbor_E = my_col + 1 <= ny_domains ? my_col + 1 : -1 neighbor_W = my_col - 1 > 0 ? my_col - 1 : -1 neighbors = Dict{String,Int}() neighbors["N"] = neighbor_N >= 0 ? id_pos[neighbor_N, my_col] : -1 neighbors["S"] = neighbor_S >= 0 ? id_pos[neighbor_S, my_col] : -1 neighbors["E"] = neighbor_E >= 0 ? id_pos[my_row, neighbor_E] : -1 neighbors["W"] = neighbor_W >= 0 ? id_pos[my_row, neighbor_W] : -1 return neighbors end
Hicimos algo similar cuando construimos laberintos
La entrada a esta función es my_id , que es el rango (o identificador) del proceso, el número de procesos nproc , el número de divisiones en la dirección x nx_domains y el número de divisiones en la dirección y ny_domains .
Veamos esta característica ahora. Por ejemplo, nuevamente mirando la fig. 5, podemos verificar la salida para el proceso de rango 4 y el proceso de rango 11. Conduzcamos a REPL:
julia> neighbors(4, 12, 3, 4) Dict{String,Int64} with 4 entries: "S" => 3 "W" => 1 "N" => 5 "E" => 7
y
julia> neighbors(11, 12, 3, 4) Dict{String,Int64} with 4 entries: "S" => 10 "W" => 8 "N" => -1 "E" => -1
Como puede ver, uso las direcciones cardinales "N", "S", "E", "W" para indicar la ubicación de un vecino. Por ejemplo, el proceso 4 tiene el proceso 3 como vecino ubicado al sur de su posición. Puede verificar que todos los resultados anteriores son correctos, dado que "-1" en el segundo ejemplo significa que no se encontraron vecinos en los lados "norte" y "este" del proceso 11.
5.2 Mensajería
Como vimos anteriormente, en cada iteración, cada proceso envía sus límites a los procesos vecinos. Al mismo tiempo, cada proceso recibe datos de sus vecinos. Estos datos son almacenados por cada proceso en forma de "células fantasmas" y se utilizan para calcular la solución cerca del límite de cada subdominio.
MPI tiene un comando muy útil MPI_Sendrecv que le permite enviar y recibir mensajes simultáneamente entre dos procesos. Desafortunadamente, MPI.jl no proporciona esta funcionalidad, sin embargo, aún es posible lograr el mismo resultado utilizando las MPI_Receive MPI_Send y MPI_Receive separado.
¡ updateBound! es lo que se ha hecho en la próxima función updateBound! , que actualiza las celdas fantasmas en cada iteración. La entrada a esta función es una solución 2D global u, que incluye celdas fantasmas, así como toda la información relacionada con un proceso específico que realiza una función (cuál es su rango, cuáles son las coordenadas de su subdominio, cuáles son sus vecinos). La función primero envía sus fronteras a los vecinos y luego recibe sus fronteras. La parte receptora se está finalizando a través del equipo MPI.Waitall! , lo que garantiza que se recibieron todos los mensajes esperados antes de actualizar las celdas laterales para un subdominio de interés particular.
Código function updateBound!(u::Array{Float64,2}, size_total_x, size_total_y, neighbors, comm, me, xs, ys, xe, ye, xcell, ycell, nproc) mep1 = me + 1
5. Visualización de la solución
El dominio se inicializa con un valor constante u = +10 alrededor del límite, que puede interpretarse como la presencia de una fuente de temperatura constante en el límite. La condición inicial u = −10 dentro de la región (Fig. 6 a la izquierda). Con el tiempo, el valor u = 10 en el límite se difunde al centro de la región. Por ejemplo, en el paso j = 15203 solución se parece a la que se muestra en la Fig. 6 a la derecha.
Con el aumento del tiempo t, la solución se vuelve más y más homogénea, mientras que en teoría no se convertirá en u = +10 todo el dominio.

Fig. 6. La condición inicial (izquierda) y la solución en el paso 15203 a tiempo (derecha). Los límites de la región siempre se almacenan en u = +10. Con el tiempo, la solución se vuelve más y más uniforme y tiende a acercarse cada vez más al valor u = +10 en toda la región.
6. Rendimiento
Me quedé muy impresionado cuando probé el rendimiento de la implementación de Julia en comparación con Fortran y C: ¡descubrí que la implementación de Julia es la más rápida!
Antes de profundizar en la comparación, veamos el rendimiento MPI del propio código de Julia. La Figura 7 muestra la relación de tiempo de ejecución cuando se trabaja con procesos 1 a 2 (CPU). Idealmente, le gustaría que este número sea cercano a 2, es decir El trabajo con dos procesadores debe ser el doble de rápido que con un solo procesador. En cambio, se observa que para tareas de pequeño tamaño (una cuadrícula de 128x128 celdas), el tiempo de compilación y la sobrecarga de comunicación tienen un impacto negativo en el tiempo de ejecución general: la aceleración es menor que uno. La ventaja de usar múltiples procesos se hace evidente solo para tareas más grandes.
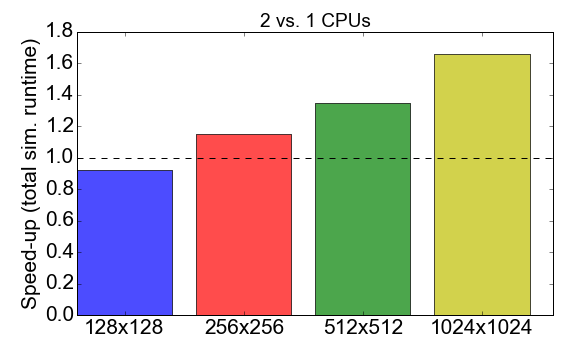
Figura 7. Acelerar la implementación de Julia MPI con dos procesos versus un proceso, dependiendo de la complejidad de la tarea (tamaño de la cuadrícula). "Aceleración" se refiere a la relación del tiempo total de ejecución usando 1 proceso a 2 procesos.
Y ahora un giro inesperado: en la fig. La Figura 8 muestra que la implementación de Julia es más rápida que Fortran y C para tareas de 256x256 y 512x512 (solo las que probé). Aquí solo mido el tiempo requerido para completar el ciclo de iteración principal. Creo que esta es una comparación justa, ya que para simulaciones largas será la mayor contribución al tiempo de ejecución general.
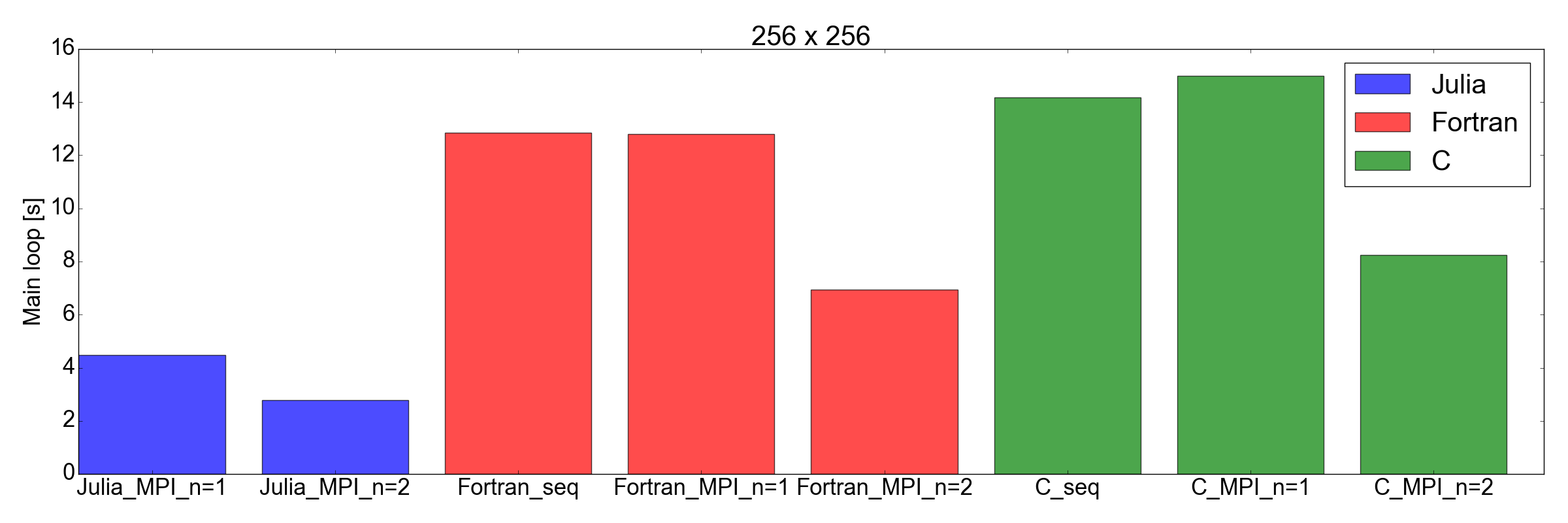

Figura 8. Rendimiento de Julia vs. Fortran vs. C para dos tamaños de cuadrícula: 256x256 (arriba) y 512x512 (abajo) Esto muestra que Julia es el lenguaje con mejor rendimiento. El rendimiento se mide como el tiempo que lleva realizar un número fijo de iteraciones en el bucle de código principal.
Conclusiones
Antes de comenzar esta publicación, era escéptico de que Julia pudiera competir con la velocidad de Fortran y C para aplicaciones científicas. La razón principal fue que anteriormente había traducido el código académico que contenía aproximadamente 2,000 líneas de Fortran a Julia 0.6, y noté una caída en el rendimiento de aproximadamente 3 veces.
Pero esta vez ... estoy muy impresionado. De hecho, acabo de traducir la implementación de MPI existente escrita en Fortran y C a Julia 1.0. Los resultados mostrados en la fig. 8, hablan por sí mismos: Julia parece ser la más rápida hasta la fecha. Tenga en cuenta que no tomé en cuenta el largo tiempo de compilación consumido por el compilador de Julia, ya que esto será un factor insignificante para las aplicaciones "reales" que requieren horas para completarse.
También debo agregar que mis pruebas, por supuesto, no son tan completas como deberían ser para una comparación exhaustiva. De hecho, me gustaría ver cómo funciona el código con más de dos procesadores (estoy limitado a la computadora portátil personal de mi hogar) y con otros equipos (ver Diffusion.jl ).
De todos modos, este ejercicio me convenció de que valdría la pena pasar más tiempo estudiando y usando a Julia para ciencia de datos y aplicaciones científicas. Ir a nuevos logros!
Referencias