Hola Habr!
Como
legisladores de
Unity en el mercado ruso, les ofrecemos leer un estudio interesante sobre el uso práctico del algoritmo WFC (Wave Function Collapse), construido a imagen y semejanza del conocido principio de la mecánica cuántica y muy conveniente para la generación de niveles de procedimientos en juegos. Anteriormente en Habré, la
historia detallada sobre este algoritmo ya estaba publicada. La autora del artículo de hoy, Marian Kleineberg, considera el algoritmo en el contexto de los gráficos tridimensionales y la generación de una ciudad sin fin. Que tengas una buena lectura!
Hablaremos de un juego en el que caminas por una ciudad interminable que se genera procesalmente a medida que te mueves. Una ciudad se construye a partir de un conjunto de bloques utilizando el algoritmo WFC (colapso de la función de onda).
El ensamblaje jugable está disponible para su descarga en el
sitio web
itch.io. También puede tomar el
código fuente en github . Finalmente, propongo un
video en el que camino por la ciudad así generada.
Algoritmo
Llamaré a la palabra "celda" un elemento de malla 3D voxel que puede contener un bloque o estar vacío. La palabra "módulo" llamaré un bloque que puede ocupar dicha celda.
El algoritmo decide qué módulos seleccionar en cada celda del mundo del juego. Una matriz de celdas se considera una función de onda en una forma no observable. Por lo tanto, cada celda corresponde a muchos módulos que pueden aparecer en ella. En términos de mecánica cuántica, se podría decir, "la célula está en una superposición de todos los módulos". La existencia del mundo comienza en una forma completamente inobservable, donde cualquier módulo puede estar en cada celda. Además, todas las células colapsan, una tras otra. Esto significa que para cada celda se selecciona aleatoriamente un módulo de todos los posibles.
El siguiente paso es la propagación de restricciones. Para cada módulo, se selecciona un subconjunto de módulos que pueden estar adyacentes a él. Cada vez que un módulo colapsa, se actualizan los subconjuntos de otros módulos, que aún se permiten como adyacentes. La etapa de propagación de restricciones es la parte del algoritmo que consume más recursos en términos de potencia informática.
Un aspecto importante del algoritmo es determinar qué célula colapsar. El algoritmo siempre colapsa la celda con la
entropía más pequeña . Esta es una celda que permite un número mínimo de opciones (es decir, una celda con la menor aleatoriedad). Si la probabilidad de colapso es la misma para todos los módulos, entonces la celda con el número mínimo de módulos posibles tendrá la entropía más baja. Como regla general, las probabilidades de ser seleccionado son diferentes para los distintos módulos disponibles. Una celda con dos módulos posibles que tienen la misma probabilidad proporciona una opción más amplia (mayor entropía) que la que tiene dos módulos, y para uno de ellos la probabilidad de caer bajo la opción es muy alta, y para el otro es muy pequeña.

(Gif publicado por
ExUtumno en Github)
Aquí se puede encontrar información más detallada sobre el algoritmo de colapso de la función de onda, así como una serie de hermosos ejemplos. Inicialmente, este algoritmo fue propuesto para generar texturas 2D basadas en una sola muestra. En este caso, los indicadores probabilísticos de los módulos y las reglas de adyacencia se determinan según su ocurrencia en el ejemplo. Este artículo proporciona esta información manualmente.
Aquí hay un
video que demuestra este algoritmo en acción.
Sobre bloques, prototipos y módulos
El mundo se genera a partir de un conjunto en el que unos 100 bloques. Los creé usando Blender. Al principio, tenía muy pocos bloques, y los agregué poco a poco cuando lo consideré necesario.

El algoritmo necesita saber qué módulos se pueden ubicar uno al lado del otro. Para cada módulo, hay 6 listas de posibles vecinos, una en cada una de las direcciones. Sin embargo, quería evitar tener que crear dicha lista manualmente. Además, quería generar automáticamente opciones rotadas para cada uno de mis bloques.
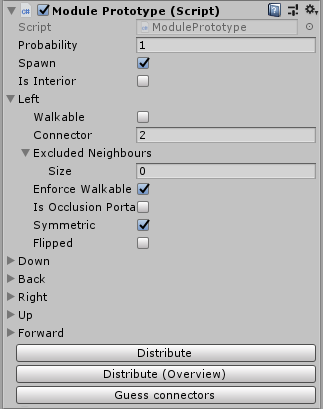
Ambas tareas se resuelven utilizando los llamados módulos prototipo. En esencia, este es
MonoBehaviour , con el cual es conveniente trabajar en el editor de Unity. Los módulos junto con las listas de elementos vecinos válidos y las opciones rotadas se crean automáticamente en función de dichos prototipos.
Surgió un problema complejo con el modelado de información de adyacencia, por lo que este proceso automático funcionó. Esto es lo que obtuve:

Cada bloque tiene 6 contactos, uno para cada cara. El contacto tiene un número. Además, los contactos horizontales pueden estar invertidos, no invertidos o simétricos. Los contactos verticales tienen un índice de rotación en el rango de 0 a 3 o están marcados como
rotacionalmente invariantes .
En base a esto, puedo verificar automáticamente qué módulos pueden encajar juntos. Los módulos adyacentes deben tener los mismos números de pin. Su simetría también debe coincidir (el mismo índice de rotación vertical, un par de contactos horizontales invertidos y no invertidos), o los módulos deben ser simétricos / invariantes.
Existen reglas de exclusión por las cuales puedo prohibir las opciones de vecindario que se permitirían por defecto. Algunos bloques con contactos coincidentes simplemente se ven feos cerca. Aquí hay un ejemplo de un mapa generado sin aplicar reglas de excepción:

Camino al infinito
El algoritmo original de colapso de la función de onda genera mapas de tamaño finito. Quería construir un mundo que se expanda y se expanda a medida que avanzas.
Al principio intenté generar fragmentos de tamaño finito y usar los contactos de fragmentos adyacentes como restricciones. Si se genera un fragmento, y también se genera un fragmento adyacente a él, entonces solo se permiten los módulos que quepan junto a los módulos existentes. Con este enfoque, surge el siguiente problema: cada vez que una celda colapsa, la propagación de restricciones reducirá las oportunidades incluso a una distancia de varias celdas. La siguiente imagen muestra los efectos de colapsar una sola celda:

Si en cada paso del algoritmo solo se genera un fragmento, las restricciones no se aplican a los fragmentos adyacentes. En este caso, dichos módulos se seleccionaron dentro del fragmento que sería inaceptable si se tienen en cuenta otros fragmentos. Como resultado, cuando el algoritmo intentó generar el siguiente fragmento, no pudo encontrar una solución única.
Ahora ya no uso fragmentos, pero almaceno el mapa en un diccionario que muestra la posición de una celda en una celda. La celda se llena solo si es necesario. Algunos elementos del algoritmo deben ajustarse teniendo esto en cuenta. Al elegir una celda que debería colapsar, es imposible tener en cuenta todas las celdas si su número es infinito. En cambio, solo generamos una pequeña porción del mapa a la vez, una vez que el jugador lo alcanza. Fuera de esta área, las restricciones continúan extendiéndose.
En algunos casos, este enfoque no funciona. Considere un conjunto de módulos para una sección recta de un túnel de la figura anterior: no hay entrada al túnel. Si el algoritmo elige dicho módulo de túnel, entonces el túnel será infinito por definición. En la etapa de distribución de restricciones, el programa intentará asignar un número infinito de celdas. Desarrollé un conjunto especial de módulos para solucionar este problema.
Condiciones de contorno
Hay dos condiciones límite importantes. Todas las caras en el nivel superior del mapa deben tener contactos "aéreos". Todas las caras en la base del mapa deben tener contactos "sólidos". Si no se cumplen estas condiciones, en el mapa habrá agujeros en el suelo y algunos edificios estarán sin techo.
En un mapa de tamaño finito, este problema se resolvería fácilmente. Para todas las celdas en el nivel más alto y más bajo, sería necesario eliminar todos los módulos con contactos inapropiados. Luego comience la distribución de restricciones y elimine los módulos restantes que ya no nos convienen.
En un mapa de tamaño infinito, esto no funcionará, porque tanto en el nivel más alto como en el más bajo, tenemos un número infinito de celdas. La solución más ingenua es eliminar todas las celdas inapropiadas inmediatamente a medida que surjan. Sin embargo, cuando se elimina un módulo en el nivel superior, se aplican restricciones a las celdas adyacentes. Hay un efecto de avalancha, que nuevamente conduce a una selección infinita de celdas.
Resolví este problema creando un mapa 1 × n × 1, donde n es la altura. Este mapa utiliza la envoltura mundial para distribuir las restricciones. El mecanismo funciona como en el juego Pacman: yendo más allá del borde derecho del mapa, el personaje vuelve a él debido al borde izquierdo. Ahora puedo aplicar cualquier restricción a mi mapa. Cada vez que crea una nueva celda en un mapa infinito, esta celda se inicializa con un conjunto de módulos que corresponden a una posición específica en el mapa.
Condiciones de error y búsqueda de retorno
A veces, el algoritmo WFC alcanza un estado en el que la celda no corresponde a ningún módulo posible. En las aplicaciones en las que estamos lidiando con un mundo de tamaño finito, simplemente puede restablecer el resultado y comenzar de nuevo. En un mundo infinito, esto no funcionará, ya que parte del mundo ya se muestra al jugador. Primero, me decidí por una solución en la que los lugares donde ocurrían los errores estaban llenos de bloques blancos.
Actualmente estoy usando la búsqueda de retorno. El orden del colapso de las celdas y cierta información sobre la distribución de restricciones se almacena en forma de historial. Si el algoritmo WFC falla, se cancela parte del historial. Como regla, esto funciona, pero a veces los errores pueden reconocerse demasiado tarde, y una búsqueda de retorno cubre muchos pasos. En casos raros, la celda en la que se encuentra el jugador se regenera.
En mi opinión, debido a esta limitación, la aplicación del algoritmo WFC con mundos infinitos no es adecuada para juegos comerciales.
Antecedentes
Comencé a trabajar en esta tarea después de ver una
conferencia de Oscar Stelberg que decía cómo usa el algoritmo para generar niveles en el juego Bad North. En general, mi algoritmo se implementó durante la semana de
procjam .
Tengo algunas ideas para un mayor refinamiento de este algoritmo, pero no estoy seguro de que algún día voy a agregarle jugabilidad. Y si me reúno, seguro que no será una estrategia tan épica como ya la habías imaginado. Sin embargo, si quieres comprobar cómo funciona tu mecánica de juego favorita con este algoritmo, ¡pruébalo tú mismo! Al final, el código fuente está disponible públicamente y tiene licencia del MIT.