Talento vs. Suerte: el papel del azar en el éxito y el fracaso

Recientemente, me encontré con un interesante trabajo de científicos italianos sobre el papel muy subestimado de la suerte y el azar en nuestras vidas. Desafortunadamente, no encontré la versión completa en ruso (¿tal vez me veía mal?), Pero realmente quería compartir lo que leía con mis camaradas de inglés que no hablaban con fluidez. Por lo tanto, arremangándose, se dedicó a su traducción artesanal. Los autores, Alessandro, Alessio y Andrea, amablemente permitieron publicarlo en el dominio público, por lo que si está interesado, bienvenido a cat.

Los autores

• A. Pluchino - Departamento de Física y Astronomía, Universidad de Catania y sucursal de Catania del Instituto Nacional de Física Nuclear, Italia; alessandro.pluchino@ct.infn.it
• A. E. Biondo - Departamento de Economía y Empresa, Universidad de Catania, Italia; ae.biondo@unict.it
• A. Rapisard - Departamento de Física y Astronomía, Universidad de Catania y sucursal de Catania del Instituto Nacional de Física Nuclear, Italia; Centro para el Estudio de Sistemas Complejos, Viena; andrea.rapisarda@ct.infn.it

Anotación

En gran medida, el liderazgo meritocrático dominante (la meritocracia es el principio de gestión, según el cual las personas más capaces, independientemente de su origen social y riqueza financiera ) , el modelo altamente competitivo de las culturas occidentales se origina en la creencia de que el éxito es principalmente, si no completamente, depende de cualidades personales como talento, inteligencia, habilidades, ingenio, trabajo duro, perseverancia, trabajo duro o toma de riesgos. A veces estamos listos para admitir que una cierta cantidad de suerte también puede desempeñar un papel en el logro de un éxito material significativo. Pero, en verdad, la importancia de las fuerzas externas en las historias de éxito individuales a menudo se subestima. Es bien sabido que la inteligencia (o, en general, el talento y las cualidades personales) en una población tiene una distribución gaussiana, mientras que la distribución de valores, a menudo vista como una medida de éxito, generalmente sigue una ley de poder (ley de Pareto) cuando la mayoría es pobre y Hay un número insignificante de multimillonarios. Esta discrepancia entre las entradas distribuidas normalmente que tienen un nivel normal (talento o inteligencia promediados) y una distribución constante en la salida sugiere que en algún lugar detrás de escena hay un componente invisible. En este documento, sobre la base de una simulación extremadamente simple y basada en un agente de juguetes, asumimos que dicho componente es un accidente ordinario. En particular, mostramos que, si bien el éxito en la vida realmente requiere una cierta cantidad de talento, las personas más talentosas casi nunca alcanzan los picos más altos de riqueza, siendo superadas por personalidades mediocres, pero mucho más exitosas. Hasta donde sabemos, este resultado contradictorio de sentido común, aunque implícitamente asumido entre líneas en una gran cantidad de literatura, fue el primero en dar una evaluación cuantitativa. Esto le permite tener una nueva visión de la efectividad de evaluar los méritos en función del nivel de éxito ya alcanzado y enfatiza los riesgos de difundir honores o recursos excesivos a personas que, a la larga, podrían ser más exitosas que otras. Usando este modelo, también consideramos y comparamos varias hipótesis de comportamiento para mostrar las estrategias más efectivas para la financiación de la investigación pública, con el objetivo de mejorar la meritocracia, la diversidad y la innovación.

1. Introducción

La ubicuidad de la dependencia de la ley de poder en muchos sistemas complejos físicos, biológicos o socioeconómicos puede considerarse como una característica matemática distintiva de la estrecha relación de sus características dinámicas con una estructura topológica sin cambios de escala [1, 2, 3, 4]. En el contexto socioeconómico, de acuerdo con el trabajo de Pareto [5, 6, 7, 8, 9], es bien sabido que la distribución de la riqueza tiene el carácter de una dependencia del poder, cuya característica forma alargada refleja la profundidad del abismo existente entre los ricos y los pobres de nuestra sociedad.

Un informe reciente [10] muestra que hoy esta brecha es mucho mayor de lo que temíamos: ocho personas poseen la misma riqueza que 3.600 millones de personas, que constituyen la parte más pobre de la humanidad. En los últimos 20 años, se han desarrollado varios modelos teóricos que calculan la distribución de valores en el contexto de la teoría de probabilidad y las estadísticas físicas, a menudo en forma de modelos de múltiples agentes con una dinámica interna simple [11, 12, 13, 14, 15, 16, 17].

Avanzando en esta dirección, si consideramos la riqueza personal como una medida de éxito, se puede argumentar que su distribución profundamente asimétrica y desigual entre las personas es una consecuencia de sus diferencias naturales en talento, habilidades, competencia, inteligencia, habilidades o la medida de su perseverancia, trabajo duro o determinación Tal suposición, de forma implícita, es la base del llamado paradigma meritocrático: afecta no solo cómo nuestra sociedad brinda oportunidades de empleo, honor y fama, sino también las estrategias adoptadas por los gobiernos para asignar recursos y financiar a quienes se consideran más honorables personalidades

Sin embargo, la conclusión anterior parece ser muy diferente de los datos confirmados de que las propiedades y cualidades de las personas mencionadas anteriormente se distribuyen normalmente en toda la población, es decir, corresponden a una distribución gaussiana simétrica en relación con este promedio. Por ejemplo, la inteligencia, medida por las pruebas de coeficiente intelectual, corresponde al siguiente patrón: el coeficiente intelectual promedio es 100, pero nadie tiene un coeficiente intelectual de 1000 o 10000. Lo mismo se aplica al trabajo contado en horas de trabajo: alguien trabaja más que el promedio, otro menos, pero no hay nadie que trabaje mil millones de horas más que el resto.

Pero en nuestro tiempo hay cada vez más evidencia sobre el papel fundamental del azar, la suerte o, en general, los factores aleatorios, en la determinación del éxito o el fracaso en nuestros asuntos personales y profesionales. En particular, se demostró que todos los científicos tienen la misma oportunidad de publicar trabajos innovadores durante sus carreras [18]; que aquellos con la primera letra del apellido más cerca del comienzo del alfabeto tienen muchas más probabilidades de recibir el cargo de jefe de departamento [19]; que las distribuciones de los indicadores bibliométricos recopilados por los científicos pueden resultar aleatorias y sin sentido debido al creciente fenómeno asociado con el mecanismo inflacionario de "publicar o morir" [20]; que la posición de alguien en una lista ordenada alfabéticamente puede ser importante para determinar el acceso a los servicios públicos limitado por el número de lugares [21]; que la letra inicial de un segundo nombre plantea una evaluación de las habilidades intelectuales [22]; que las personas con nombres fácilmente pronunciados se califican más positivamente que aquellas cuyos nombres son complejos [23]; que aquellos cuyos nombres suenan más aristocráticos con más frecuencia que otros trabajan como líderes y no como subordinados [24]; que las mujeres con apodos masculinos tienen más éxito en la profesión legal [25]; que aproximadamente la mitad de las diferencias de ingresos entre las personas en todo el mundo se explica únicamente por su país de residencia y la distribución de los salarios dentro del país respectivo [26]; que la probabilidad de convertirse en director está muy influenciada por su nombre y mes de nacimiento [27, 28, 29]; que las ideas innovadoras son el resultado de reacciones aleatorias en las células de nuestro cerebro [30]; y que incluso la probabilidad de desarrollar cáncer, posiblemente destruyendo una carrera excelente, en su mayor parte depende del fracaso [31, 32]. Trabajos recientes sobre el tema del éxito reproductivo a lo largo de la vida contribuyen a la confirmación de tales declaraciones, mostrando que si las desviaciones de los rasgos pueden afectar el destino de la población en su conjunto, la vida de individuos específicos a menudo está determinada por la suerte.

En los últimos años, muchos autores, incluidos el estadístico y analista de riesgos Nassim Taleb [35, 36], el estratega de inversiones Michael Mobussin [37] y el economista Robert Frank [38], han investigado en varios libros populares la conexión entre la suerte y la habilidad en las transacciones financieras, negocios, deportes, arte, música, literatura, ciencia y muchas otras áreas. Llegaron a la conclusión de que los eventos aleatorios juegan un papel mucho más importante en la vida de lo que muchos habrían imaginado. De hecho, no asumen que el éxito no depende del talento y los esfuerzos, ya que en áreas o mercados extremadamente competitivos como "el ganador se lo lleva todo", donde vivimos y trabajamos en este momento, las personas más productivas son casi siempre extraordinarias. talentoso y trabajador. Solo concluyeron que el talento y el esfuerzo no son suficientes: también debes estar en el lugar correcto en el momento correcto. En resumen, la suerte también afecta, aunque su papel casi siempre es subestimado por las personas exitosas. Esto se debe al hecho de que la aleatoriedad a menudo funciona de una manera no obvia, por lo que es fácil comparar eventos que muestran el éxito como algo inevitable. Taleb llama a esa inclinación "una falacia fantástica" [36], y el sociólogo Paul Lazarsfeld propuso el término "retrospectiva sesgada". En su último libro, "Everything Is Obvious: When You Know the Answer" [39], el sociólogo y pionero de la ciencia de redes Duncan Watts sugiere que tanto el engaño fabuloso como la atracción retrospectiva sesgada a un fenómeno especial en el que las personas que ven resultados inusualmente exitosos, considérelos como un producto indudable de trabajo duro y talento. Sin embargo, el éxito surge principalmente a través de pasos complejos y entrelazados, cada uno de los cuales depende de los anteriores: si alguno de ellos fuera diferente, toda la carrera o el camino de la vida seguramente también serían diferentes. Este argumento también se basa en los resultados de un innovador estudio experimental realizado varios años antes por el propio Watts en colaboración con otros autores [40], en el que el éxito de canciones previamente desconocidas en el mercado de la música artificial no se correlacionó con la calidad del trabajo en sí. Y esto, por supuesto, complica enormemente cualquier predicción, como se muestra en otro estudio más reciente [41].

En este documento, utilizando un enfoque estadístico basado en agentes, intentaremos determinar prácticamente de manera cuantitativa el papel de la suerte y el talento en carreras exitosas. En la Sección 2, basada en el número mínimo de supuestos, a saber, la naturaleza gaussiana de la distribución del talento [42] y la dinámica multiplicativa de éxitos y fracasos [43], presentamos un modelo simple, que se llamó el modelo “Talento vs. Suerte” (TPU), que imita el desarrollo de carreras profesionales de un grupo de personas durante el período de 40 años de su trabajo. El modelo muestra que, en realidad, la aleatoriedad juega un papel fundamental en la determinación de los individuos más exitosos. Lo cierto es que, como cabría esperar, las personas con talento tienen más probabilidades de hacerse ricas, famosas o importantes en sus propias vidas, en relación con las menos preparadas. Pero, y esta explicación menos intuitiva, las personas comunes con un nivel ordinario de talento están estadísticamente destinadas a tener éxito (es decir, a ubicarse al final de una distribución de poder de éxito) con mucha más frecuencia que los más talentosos, siempre que se conviertan en favoritos de la fortuna para de tu vida Este hecho a menudo se encuentra, como se indica en las referencias [35, 36, 38], pero, hasta donde sabemos, primero se modeló y midió en este trabajo.

El éxito de las personas con talento ordinario pone en tela de juicio el paradigma "meritocrático" y todas esas estrategias y mecanismos que otorgaron más recompensas, oportunidades, honor, fama y recursos a las personas consideradas las mejores en su campo [44, 45]. El hecho es que, en la gran mayoría de los casos, todas las evaluaciones del talento de alguien se realizaron después del hecho, únicamente al observar su actividad o los resultados alcanzados, en un área específica de nuestra sociedad, como deportes, negocios, finanzas, arte , ciencia, etc. Este tipo de evaluación engañosa conduce a una sustitución de causa y efecto, evaluando como las personas más talentosas aquellas que son, simplemente, las más exitosas [46, 47]. De acuerdo con este punto de vista, trabajos anteriores advirtieron sobre tipos similares de "casi meritocracia" y mostraron la efectividad de otras estrategias basadas en muestras aleatorias en muchos entornos diferentes, como la gestión, la política y las finanzas [48, 49, 50, 51, 52, 53, 54, 55]. En la Sección 3, aplicamos nuestro enfoque y describimos cómo es posible la distribución de fondos públicos en el contexto de la investigación científica. Estudiamos las consecuencias de varias estrategias de distribución, entre las cuales hay una "casi" meritocrática, con el objetivo de explorar nuevas formas de aumentar, al mismo tiempo, el nivel mínimo de éxito de las personas más talentosas de la sociedad y la eficiencia total del gasto público. También examinaremos, en general, cómo las oportunidades ofrecidas por el medio ambiente, presentadas en forma de educación y niveles de ingresos (es decir, factores externos que dependen del país y la capa social de donde provienen las personas), son importantes para aumentar la probabilidad de éxito. Las observaciones finales completan el trabajo.

2. Modelo

Además, proponemos un modelo de agente llamado "Talento contra la suerte" (TPU), basado en un pequeño número de suposiciones, y con el objetivo de describir la evolución de las carreras de un grupo de personas bajo la influencia de eventos exitosos y no exitosos que ocurren al azar.


Figura 1: Un ejemplo de los parámetros iniciales para nuestra simulación. Todas las simulaciones presentadas en este documento se llevaron a cabo en el entorno de simulación del agente de NetLogo [56]. N = 1000 personas (agentes), con diversos grados de talento (inteligencia, habilidades, etc.) distribuidos aleatoriamente en posiciones fijas dentro del mundo cuadrado de 201 × 201 secciones con condiciones de límites cíclicos. Durante cada simulación, que abarca varias décadas, se exponen a una cierta cantidad de eventos N _E exitosos (círculos verdes) y no exitosos (círculos rojos) que se mueven alrededor del mundo a lo largo de trayectorias aleatorias (caminata aleatoria). En este ejemplo, N _E = 500.

Consideramos que N individuos con talento T _i (intelecto, habilidades, habilidades, etc.) tienen una distribución normal en el intervalo [0; 1] alrededor de un promedio m m dado con una desviación estándar σ _T colocada aleatoriamente en posiciones fijas dentro del mundo cuadrado (ver Figura 1) con condiciones de límite cíclicas (es decir, con una topología toroidal) y rodeada por un cierto número N _{E de} "movimiento" eventos (marcados con puntos), algunos de los cuales son exitosos, ningún otro (los eventos neutrales en este modelo no se tienen en cuenta, ya que no tienen consecuencias significativas en la vida del individuo). En la Figura 1, mostramos estos eventos en forma de puntos de colores: exitosos en verde y con un porcentaje relativo p _L , y sin éxito en rojo y con un porcentaje ( 100 - p _L ). El número total de puntos de evento N _E se distribuye uniformemente, pero, por supuesto, dicha distribución será idealmente uniforme solo para N _E → ∞ . En nuestras simulaciones, generalmente habrá N _E ≈ N / 2 , por lo tanto, al comienzo de cada simulación, hay una concentración aleatoria significativa de puntos de eventos exitosos o no exitosos en varias regiones del mundo, mientras que otras regiones serán más neutrales. El movimiento aleatorio posterior de puntos dentro de una matriz cuadrada, es decir, el mundo, no cambia esta característica fundamental del modelo, que indica un número diferente de eventos de éxito o fracaso para diferentes personas a lo largo de sus vidas, sin depender de su talento personal.


Figura 2: distribución normal del talento entre la población (con la mediana m _T = 0.6 mostrada por una línea vertical discontinua y la desviación estándar σ _T = 0.1 - los valores m _T ± σ _{T se} muestran como dos líneas verticales punteadas). Esta distribución se asigna en el intervalo [0; 1] y no cambia durante la simulación.

Una ejecución de simulación examina un período de vida laboral P de 40 años (de veinte a sesenta años), con un paso de tiempo δ _t de seis meses. Al comienzo de la simulación, todos los agentes recibieron el mismo capital C _i = C (0) Ɐ _i = 1, ..., N , que representa su nivel inicial de éxito / bienestar. Esta elección tiene el objetivo obvio de no darle a nadie la ventaja inicial. Si bien los talentos de los agentes no dependen del tiempo, su capital está cambiando. Durante el desarrollo de este modelo, es decir, durante el período esperado de la vida de los agentes, todos los puntos de evento se mueven aleatoriamente alrededor del mundo y, al mismo tiempo, pueden cruzarse con la ubicación de algunos agentes. Si entra en detalles, cada vez que cada punto de evento cubre, en una dirección aleatoria, la distancia de 2 secciones. Creemos que hay una intersección con el individuo si el punto de evento representado dentro del círculo con un radio de un segmento está centrado en el agente (los puntos de evento no desaparecen después de la intersección).Dependiendo de tal incidente, en este momento el paso t (es decir, cada seis meses), con un cierto agente A _k , son posibles las siguientes tres opciones posibles:

1. Ningún punto de evento cruza la posición del agente A _k ; esto significa que durante los últimos seis meses no se han producido tales eventos, el agente A _k no realiza ninguna acción.
2. A _k – , ( , [30], , ); , A _k / , T _k . C _k (t) = 2C _k (t − 1) , rand[0; 1] < T _k , .., , .
3. A _k – , ; , A _k / , .. C _k (t) = C _k (t − 1) / 2 .

Las reglas anteriores para los agentes (incluida la opción de dividir el capital inicial a la mitad en caso de eventos fallidos y duplicar en caso de eventos exitosos, en proporción al talento del agente) son intencionalmente simples y pueden considerarse generalizadas, ya que se basan en el hecho obvio de que el éxito en la vida cotidiana tiene la propiedad ambos crecen y disminuyen a un ritmo rápido. Además, estas reglas brindan una ventaja significativa a las personas con mucho talento, ya que pueden beneficiarse más de las oportunidades que presenta la suerte (incluida la capacidad de utilizar una buena idea que se originó en sus cerebros). Por otro lado, por ejemplo, un accidente automovilístico o una enfermedad repentina, siempre son eventos fallidos en los que el talento no importa. En este sentido, podemos derivar una definición más precisa de "talento",definiéndolo como "cualquier cualidad personal que aumenta la posibilidad de aprovechar la oportunidad". En otras palabras, con el término "talento" nosotros, en sentido amplio, queremos decir inteligencia, habilidades, ingenio, tenacidad, determinación, trabajo duro, toma de riesgos, etc. Además, veremos que la ventaja de tener un gran talento es una condición necesaria pero no suficiente para alcanzar picos de éxito muy altos.

2.1. Resultados de una carrera

En esta subsección presentamos los resultados de una ejecución de una simulación típica. En términos generales, estos resultados son bastante estables, por lo tanto, como mostramos a continuación, se puede considerar que son sustancialmente representativos del marco general que deja nuestro modelo.

Imaginemos N = 1000 agentes con una cantidad igual de capital inicial C (0) = 10 (en unidades abstractas) y con un talento fijo T _i ϵ [0; 1], la siguiente distribución normal con una mediana m _T = 0.6 y una desviación estándar σ _T = 0.1 (ver Figura 2). Como se mencionó anteriormente, la simulación cubre un lapso de tiempo realista P= 40 años, desarrollándose en pasos iguales, seis meses cada uno, en total a partir de I = 80 iteraciones. En esta simulación, tomamos N _E = 500 puntos de evento, con la probabilidad de eventos exitosos p _L = 50%.

Al final de la simulación, como se puede ver en el esquema (a) de la Figura 3, encontramos que las reglas de modelos dinámicos simples pueden producir una distribución desigual de capital / éxito, con una gran cantidad de agentes pobres (sin éxito) y una pequeña cantidad de agentes extremadamente ricos (exitosos). Habiendo construido la misma distribución en una escala bilogarítmica, en el esquema (b) de la misma figura vemos la distribución de acuerdo con la función de potencia en el estilo de Pareto, cuya pendiente corresponde a la función y © ≈ C ^−1.27 .

Por lo tanto, a pesar de la distribución normal del talento, el modelo TPU parece haber podido capturar la primera característica importante observada en comparación con los datos reales: la brecha más profunda entre ricos y pobres y la naturaleza invariable de su escala. En particular, en nuestra simulación solo 4 personas recibieron más de 500 unidades de capital, y las 20 personas más exitosas poseen el 44% de todos los valores, mientras que casi la mitad de la población tiene menos de 10 unidades. En general, se observa la regla de Pareto "80/20", ya que el 80% de la población posee solo el 20% del capital total, mientras que el 20% restante de las personas tiene el 80% de la riqueza. Aunque esta desigualdad sin duda parece injusta, sería algo aceptable si la mayoría de las personas exitosas estuvieran entre las más talentosas,ganando así más acumulación / éxito de capital que el resto. ¿Pero esto realmente está sucediendo?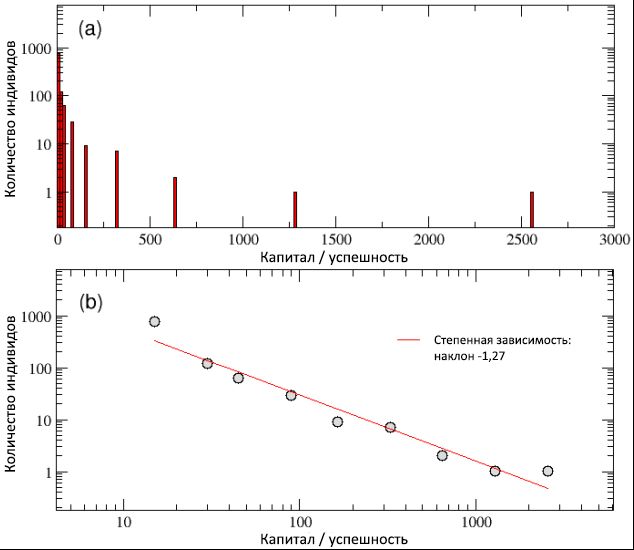


Figura 3: La distribución final de riqueza / éxito entre la población, en una escala logarítmica lineal (a) y bilogarítmica (b). A pesar de la distribución normal del talento, la cola de la distribución del éxito, como puede verse en el esquema (b), puede describirse como una curva de potencia con una pendiente de -1,27. También hemos confirmado que la distribución de capital / éxito sigue la ley Pareto "80/20", ya que el 20% de la población posee el 80% de los valores y viceversa.

En la Fig. 4, los esquemas (a) y (b), respectivamente, el talento se muestra en función del capital / éxito total, y viceversa (tenga en cuenta que en el esquema (a) el capital / éxito solo tiene valores discretos; esto está relacionado con la decisión usar el mismo capital inicial para todos los agentes). Una mirada a ambos esquemas muestra que, por un lado, las personas más exitosas no son las más talentosas y, por el contrario, las personas más talentosas no son las más exitosas. En particular, el individuo más exitoso, con C _max = 2560, tiene el talento T * = 0.61, que es solo un poco más alto que el valor medio m _T = 0.6, mientras que el más talentoso ( T _max= 0.89) tiene una tasa de capital / éxito de menos de 1 unidad ( C = 0.625).

Como aprendemos con más detalle en la siguiente subsección, este resultado no es un caso especial, sino más bien una regla para sistemas de este tipo: el éxito máximo nunca coincide con el talento máximo, y viceversa. Además, esta discrepancia entre el éxito y el talento es desproporcionada y altamente no lineal. De hecho, el capital promedio de todas las personas con talento T> T * es C≈ 20; en otras palabras, el capital / éxito de las personas más exitosas con talentos moderados es 128 veces mayor que el capital / éxito promedio de las personas que tienen mucho más talento que los primeros. Podemos concluir que si un talento excepcional no se oculta detrás de la razón del tremendo éxito de algunas personas, entonces, quizás, haya otro factor. Nuestra simulación muestra claramente que la pura suerte es un factor.


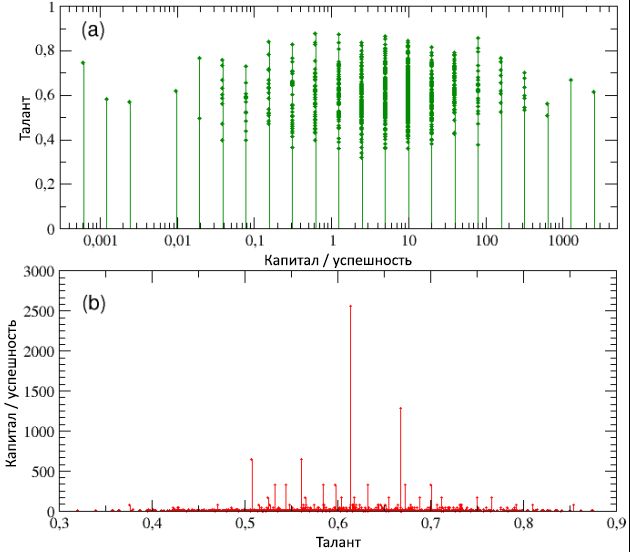Figura 4: en el diagrama (a), el talento se muestra en función del capital / éxito (en una escala logarítmica, para una mejor visualización): indica que los individuos más exitosos no son, al mismo tiempo, los más talentosos. En el diagrama (b), por el contrario, el capital / éxito se muestra en función del talento: aquí puede evaluar mejor el hecho de que el agente más exitoso, con C _max= 2560, tiene un talento que solo excede ligeramente el valor medio m _T = 0.6, mientras que el más talentoso tiene un capital / éxito menor que C = 1 unidad, mucho menos que el capital inicial C (0). Sigue leyendo para más detalles.

En la Figura 5, el número de eventos exitosos y no exitosos que ocurrieron con todas las personas durante el período de su vida laboral se muestra en función de su capital / éxito total. Al considerar el esquema (a), resulta obvio que las personas más exitosas son al mismo tiempo las más exitosas (tenga en cuenta que este diagrama muestra todos los eventos exitosos que les sucedieron a los agentes, y no solo aquellos de los que pudieron beneficiarse, de acuerdo con con tu talento). Por el contrario, cuando observamos el esquema (b), vemos que los que no tienen éxito al mismo tiempo son los que no tienen éxito. En otras palabras, aunque no existe una correlación entre el éxito y el talento, según las simulaciones, existe una fuerte dependencia del éxito en la suerte. Analizando los detalles de las distribuciones de frecuencia del número de eventos exitosos y no exitosos que ocurrieron con individuos, encontramoscomo se muestra en los diagramas © y (d) que ambos valores son exponenciales, con grados de 0,64 y 0,48, y medianas de 1,35 y 1,66, respectivamente, y que se produjeron los números máximos de eventos exitosos y no exitosos, respectivamente, 10 y 15. Además, aproximadamente el 16% tenía una vida "neutral", generalmente sin eventos exitosos y no exitosos, mientras que el 40% de las personas encontraron solo un tipo de evento (exitoso o no exitoso).mientras que el 40% de las personas encontraron solo un tipo de evento (exitoso o no exitoso).mientras que el 40% de las personas encontraron solo un tipo de evento (exitoso o no exitoso).

También es interesante observar el período de desarrollo de éxito / capital tanto para los individuos más exitosos como para los que no tuvieron éxito, en comparación con las secuencias correspondientes de eventos exitosos y no exitosos que ocurrieron durante 40 años (80 intervalos, 6 meses cada uno) de su vida laboral. Los resultados se pueden ver, respectivamente, en las partes izquierda y derecha de la Figura 6. A diferencia del esquema (a) de la imagen 5, los esquemas inferiores de esta figura contienen solo aquellos eventos exitosos de los cuales los agentes, gracias a su talento, pudieron beneficiarse.


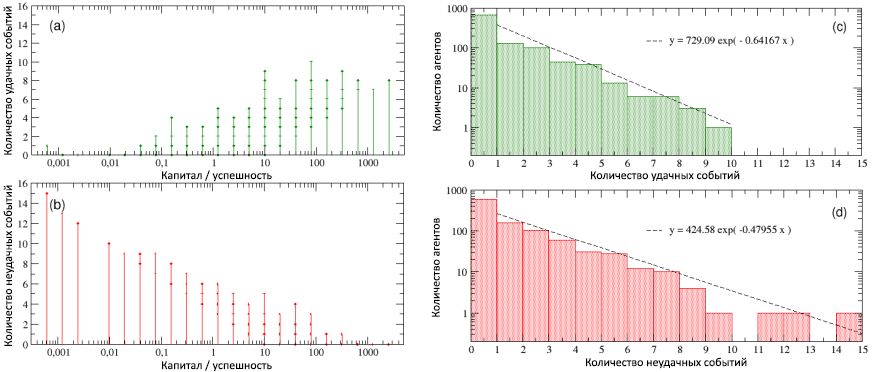Figura 5: número total de eventos exitosos (a) y no exitosos (b), como funciones del éxito del capital / agente. El gráfico muestra una fuerte correlación entre el éxito y el éxito: los individuos más exitosos también son los más exitosos, y viceversa. Nuevamente, debido al uso del mismo capital inicial para todos los agentes, resulta que varios eventos se agrupan en valores discretos de capital / éxito. En los esquemas © y (d), la frecuencia de las distribuciones, respectivamente, del número de eventos exitosos y no exitosos se muestra en una escala logarítmica lineal. Como se puede ver, ambas distribuciones se pueden escribir en forma de dependencias exponenciales con poderes negativos similares).

En los diagramas (superior e inferior) (a) de la Figura 6, sobre un individuo moderadamente talentoso pero más exitoso, se ve claramente que después de aproximadamente la mitad de su vida laboral, acompañado de una manifestación rara de eventos exitosos (diagrama inferior) y un bajo nivel de capital (superior esquema), la concentración repentina de eventos favorables que ocurrieron entre 30 y 40 pasos de tiempo (es decir, justo antes del 40 cumpleaños del agente) condujo a un rápido aumento de capital, que en los últimos 10 pasos (es decir, en los últimos 5 años de la carrera del agente ) se volvió exponencial al pasar de C = 320 a C _máx = 2560.

Por otro lado, al observar los diagramas (superior e inferior) (b) de la misma figura con respecto al individuo menos exitoso, resulta obvio que una segunda mitad de su vida laboral particularmente infructuosa, acompañada de una docena de eventos adversos, reduce constantemente el capital / éxito, lo que lleva al final valor C = 0,00061. Es interesante notar que el talento de este desafortunado agente era T= 0,74, que es más alto que la mayoría de los más exitosos. Obviamente, la creación de la diferencia fue influenciada por la suerte. Y si es cierto que el agente más exitoso mereció beneficiarse de todas las oportunidades que se le brindan (a pesar de su talento mediocre), también es cierto que si su vida está llena de desgracias y no brinda oportunidades, como este segundo agente, entonces incluso el mayor talento se vuelve impotente contra el fracaso violento.


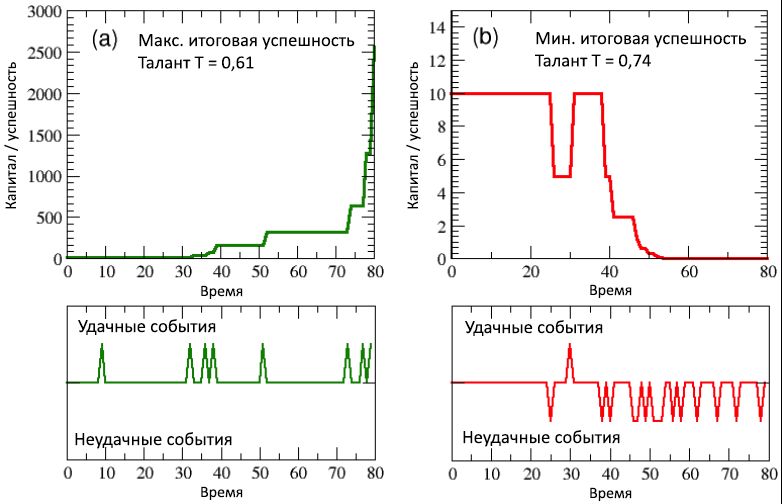Figura 6: (a) el período de desarrollo del éxito / capital del individuo más exitoso y (b) el más desafortunado, en comparación con las secuencias correspondientes de eventos exitosos y no exitosos que ocurrieron durante su vida laboral (de 80 medios años, es decir, 40 años). El tiempo de ocurrencia de tales eventos se observa en los diagramas inferiores en forma de picos ascendentes y descendentes.

Todos los resultados de una sola ejecución (la versión de demostración del código NetLogo del modelo TPU utilizado para esta simulación se puede encontrar en el repositorio Open ABM) presentado en esta subsección son muy estables y, como veremos en la siguiente subsección, se guardan, con ligeras diferencias, con muchas repeticiones de simulaciones que comienzan con la misma distribución de talento, pero con diferentes posiciones aleatorias de los individuos.

2.2. Resultados de ejecución múltiple

En esta subsección, presentamos los resultados de la simulación general de, en promedio, más de 100 corridas, cada una de las cuales comenzó con condiciones iniciales diferentes, seleccionadas al azar. Los valores de los parámetros de control fueron los mismos que en la subsección anterior: N = 1000 individuos, m _T = 0.6 y σ _T = 0.1 para la distribución normal del talento, I = 80 iteraciones (cada una representa δ _t = 6 meses de vida laboral ), C (0) = 10 unidades de capital inicial, N _E = 500 puntos de evento y el porcentaje de eventos exitosos p _L = 50%.

En el diagrama (a) de la Figura 7, la distribución total del capital / éxito total entre todos los agentes recolectados como resultado de 100 corridas se muestra en una escala logarítmica y está bien descrita por una curva de ley de potencia con un coeficiente angular −1.33. La propiedad de la constancia del capital observada en una sola ejecución independientemente de la escala y la alta desigualdad resultante entre los individuos, así como la regla de Pareto "80/20", se conservan en el caso de varias ejecuciones. De hecho, la brecha entre los agentes ricos (exitosos) y pobres (no exitosos) incluso se ha ampliado, ya que la capital de las personas más ricas ha excedido las 40,000 unidades.

Este resultado se puede estimar mejor observando el esquema (b) de la Figura 7, donde la _{Cmax de} capital total _de solo los individuos más exitosos se muestra en función del talento mostrando el mejor resultado en cada una de las 100 carreras. El agente con el talento T _mejor = 0.6048, casi coincidiendo con la mediana de la distribución del talento ( m _T = 0.6), que alcanzó el pico de capital C _mejor = 40960, recibió la mayor cantidad de puntos. Por otro lado, el más talentoso de los individuos más exitosos, con talento T _max = 0.91, capital ganado C _max = 2560, que es solo el 6% de C _mejor .


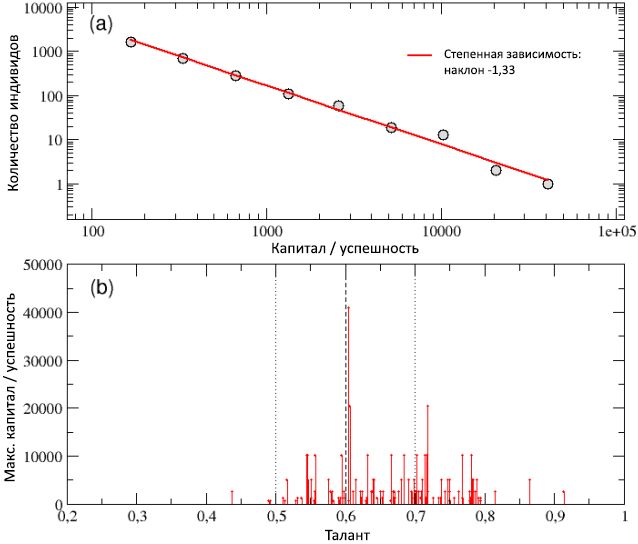
Figura 7: Esquema (a): distribución del capital total / éxito calculado sobre 100 corridas para poblaciones con diferentes condiciones iniciales determinadas al azar. La distribución se puede describir mediante una curva de potencia con una pendiente de -1.33. Esquema (b): la _{Cmax de} capital total _{de las personas} más exitosas en cada una de las 100 carreras, que se muestra en función de su talento. Las personas con talento moderadamente alto, en promedio, son más exitosas que aquellas que tienen talento bajo o moderadamente bajo, y la mayoría de las veces el individuo más exitoso es un agente moderadamente talentoso, y solo ocasionalmente el más talentoso. El valor de m _T , así como los valores de m _T ± σ _T , se muestran, respectivamente, en forma de líneas discontinuas y punteadas verticales.

Para considerar este punto de vista con más detalle, en la Figura 8 (a) trazamos la distribución del talento de los mejores artistas, calculada para 100 carreras. La distribución, obviamente, se desplaza hacia la derecha a lo largo del eje del talento, con un valor promedio de T _av = 0.66> m _T ; esto confirma, por un lado, que para lograr un éxito significativo, a menudo es necesario un talento moderadamente alto; sin embargo, por otro lado, también muestra que esta condición casi nunca es suficiente, ya que los agentes con el talento más alto (es decir, con T > m _T = 2σ _T , o T > 0.8) solo se encuentran entre los mejores. en el 3% de los casos, y su capital / éxito nunca supera el 13% de C _mejor .


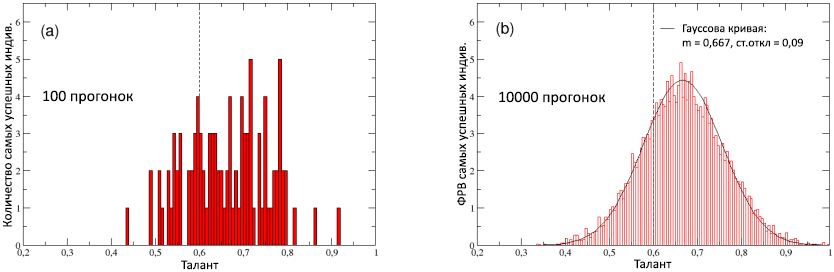
Figura 8: (a) Distribución de talentos de las personalidades más exitosas (mejor desempeño) en cada una de las 100 carreras. (b) La función de distribución de probabilidad (RFF) del talento de los individuos más exitosos, calculada en 10,000 carreras: está bien descrita por la distribución normal con una mediana de 0.667 y una desviación estándar de 0.09 (curva sólida). A modo de comparación, se muestra la mediana m _T = 0.6 de la distribución normal inicial del talento en la población, mostrada en ambos esquemas por una línea vertical discontinua.

En el diagrama (b) de la Figura 8, se calcula la misma distribución (reducida al área total para obtener el FRF) para 10,000 ejecuciones con el fin de comprender su verdadera forma: parece que encaja en la curva Gaussiana G (T) con el promedio T _av = 0.667 y una desviación estándar de 0.09 (línea continua). Esto, por supuesto, confirma que la distribución del talento de los mejores artistas se desplaza hacia la derecha en relación con el eje del talento, en comparación con la distribución inicial. Para ser más precisos, esto significa que la probabilidad condicional P ( C _max | T ) = G (T) dT para encontrar entre los mejores intérpretes una personalidad con talento en el intervalo [ T ; T + dT ] crece con el talento T , alcanza un pico cercano al talento moderado-medio T _av = 0.66, y luego cae bruscamente con grandes valores de talento. En otras palabras, la probabilidad de encontrar un individuo moderadamente talentoso en la cima del éxito es mayor que encontrar allí a una persona muy talentosa. Tenga en cuenta que en un mundo ideal en el que el talento era la razón principal del éxito, se espera que P ( C _max | T ) sea una función creciente de T. Por lo tanto, podemos concluir que la forma gaussiana observada P ( C _max | T ) es evidencia de una mayor importancia de la suerte que el talento para lograr niveles extremadamente altos de éxito.


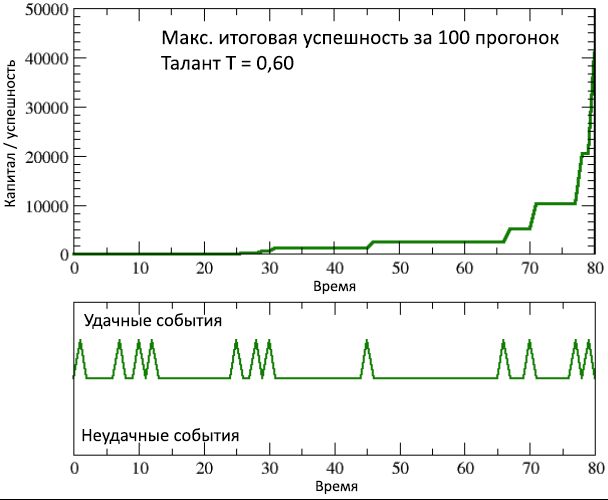
Figura 9: cambio en el tiempo de éxito / capital de la persona más exitosa (pero al mismo tiempo, moderadamente dotada), de 100 ejecuciones de simulación, en comparación con la secuencia inusual correspondiente de eventos exitosos que ocurrieron en su vida.

También es interesante comparar, a partir de 100 carreras, la tasa de capital / éxito promedio C _mt ≈ 63 de las personas más talentosas con el promedio C correspondiente _en ≈ 33 de aquellos cuyo talento está cerca de la mediana m _T. En ambos casos, encontramos indicadores bastante bajos (incluso si es más que el capital inicial C (0) = 10), pero el hecho de que C _mt > C _en indica que aunque la probabilidad de encontrar un individuo moderadamente talentoso en la cima del éxito es mayor, que el que es altamente talentoso, los individuos más talentosos de cada carrera son, en promedio, más exitosos que las personas moderadamente talentosas. Por otro lado, observando el promedio de más de 100 carreras, la proporción de individuos con talento T > 0.7 (es decir, mayor que con una desviación estándar de la mediana) y el éxito final / capital C _final > 10, calculado teniendo en cuenta todos los agentes con talento T > 0.7 (de los cuales, en promedio para cada carrera, ≈ 160), encontramos que esta participación es del 32%, esto significa que el rendimiento combinado de las personas más talentosas de nuestra población es, en promedio, relativamente pequeño, ya que solo un tercio de ellos alcanza un capital total que excede el original.

En cualquier caso, el hecho de que el mejor jugador entre las 100 carreras de simulación sea un agente con el talento T _best = 0.6, que coincide perfectamente con la mediana, y con el éxito final C _best = 40960, que es 650 veces más que C _mt , es _irrefutable . y más de 4,000 veces mayor que el éxito de C _final <10 en 2/3 de las personas más talentosas. Esto sucedió, al final, simplemente porque tuvo más suerte que el resto. Suerte incondicional, como se puede ver en la Figura 9, que muestra el crecimiento de su capital / éxito durante su vida laboral, junto con una impresionante serie de eventos exitosos (y solo exitosos), de los cuales, a pesar de la falta de talento excepcional, pudo obtener ganancias durante su carreras

En resumen, en este punto se descubrió que, a pesar de su simplicidad, el modelo TPU parece ser capaz de tener en cuenta muchas características que caracterizan, como se mencionó en la introducción, la alta desigualdad en la distribución de la riqueza y el éxito en nuestra sociedad, lo que contrasta claramente con la distribución gaussiana del talento entre personas Además, el modelo en forma cuantitativa muestra que un gran talento no es suficiente para una carrera exitosa garantizada y que, por el contrario, las personas menos talentosas a menudo alcanzan el pináculo del éxito; este es otro "hecho condicional" que a menudo se observa en la vida real [35, 36, 38].

Un aspecto clave que explica intuitivamente cómo puede suceder que las personas moderadamente talentosas logren (con tanta frecuencia) un honor y un éxito mucho mayores, en comparación con los más talentosos, es que existe un papel oculto y a menudo subestimado de la suerte, ya que es claramente visto desde nuestras simulaciones. Pero para comprender el verdadero significado de los resultados de nuestra investigación, es importante distinguir entre los puntos de vista macro y micro.

De hecho, a nivel micro, siguiendo las reglas dinámicas del modelo TPU, un individuo dotado es a priori más propenso a alcanzar un alto nivel de éxito que uno moderadamente talentoso, ya que tiene una mayor capacidad para aprovechar la oportunidad. Por lo tanto, desde el punto de vista de un individuo, debemos concluir que, al no poder (por definición) influir en la aparición de eventos exitosos, la mejor estrategia para aumentar la probabilidad de éxito (en cualquier nivel de talento) es expandir la actividad personal, generar ideas, comunicarse con otras personas, la búsqueda de la diversidad y el enriquecimiento mutuo. En otras palabras, convertirse en una persona de mente abierta que está lista para contactar a otros brinda la mayor probabilidad de un evento exitoso (que se realizará en la medida del talento del individuo).

Por otro lado, en el nivel macro, desde el punto de vista de toda la sociedad, la probabilidad de encontrarse con personas moderadamente talentosas en la cima del éxito es mucho mayor que encontrar personas extremadamente talentosas allí, porque las primeras son mucho más grandes y, gracias a la suerte, tienen, en general, estadísticas La ventaja de lograr un tremendo éxito, a pesar de su propia probabilidad personal a priori menor.

En la siguiente sección, consideraremos este punto de vista a nivel macro, explorando las oportunidades que ofrece nuestro modelo para estudiar con más detalle estrategias y políticas más efectivas para mejorar el nivel promedio de desempeño de las personas más talentosas de la población, implementando formas más productivas de distribuir recompensas y recursos. De hecho, esperamos que cualquier política que pueda aumentar el nivel de las personas más talentosas que son el motor del progreso y la innovación en nuestra sociedad tendrá un efecto beneficioso acumulativo.

3. Estrategias efectivas para equilibrar la suerte

Los resultados presentados en la sección anterior son claramente consistentes con la evidencia empírica documentada en la introducción, que cuestiona la suposición meritocrática de que las diferencias naturales en talento, habilidades, habilidades, inteligencia, trabajo duro o perseverancia son las únicas razones para el éxito. Como hemos demostrado, la suerte también tiene un impacto y puede desempeñar un papel crucial. La esencia de la discusión es que, debido a la difícil capacidad de medición (en muchos casos, es difícil determinar en términos exactos) de las cualidades personales, las estrategias meritocráticas a menudo se utilizan para distribuir honores, financiamiento o premios, a menudo basados ​​en resultados privados, medidos en términos de riqueza personal o éxito. Como resultado, tales estrategias influyen en la acción de fortalecimiento adicional y aumentan la riqueza / éxito de las personas más exitosas debido al mecanismo de retroalimentación positiva, que es similar al proceso de "enriquecerse enriquecerse" (también conocido como el "efecto Mateo" [57, 58, 59]) , con un resultado injusto.

Imaginemos, por ejemplo, un consejo de investigación y desarrollo financiado por el gobierno con una cantidad fija de dinero a su disposición. ¿Qué será mucho más efectivo para aumentar la efectividad promedio de la investigación: otorgar grandes subvenciones a solo unos pocos científicos sin duda excelentes o pequeñas subvenciones a muchos científicos obviamente más comunes? Un estudio reciente [44], basado en un análisis de cuatro índices de la importancia científica de publicaciones relacionadas, encontró que la importancia solo tiene una relación positiva débil con la financiación. En particular, la importancia del dólar fue menor para los grandes titulares de subvenciones, y la importancia de los científicos que recibieron aumentos en la financiación no aumentó en un grado apropiado. Los autores del estudio concluyeron que la importancia científica (como se refleja en la publicación) solo limita débilmente con el financiamiento, y sugirieron que las estrategias de financiamiento destinadas a diversificar las ideas en lugar de la "excelencia" probablemente sean más productivas. Una contribución posterior [60] mostró que, tanto en el número de documentos producidos como en su importancia científica, la financiación concentrada de la investigación generalmente conduce a rendimientos marginales decrecientes, y también que los investigadores más financiados no se destacan en términos de efectividad y significado científico. En general, tales conclusiones no deberían sorprender a la luz de otro descubrimiento reciente [18], que establece que la importancia, medida por publicaciones influyentes, se distribuye aleatoriamente en varias publicaciones del científico. En otras palabras, la suerte importa, y si afecta más de lo que queremos admitir, no es sorprendente que las estrategias meritocráticas sean menos efectivas de lo esperado, especialmente si estamos tratando de apreciar el mérito a posteriori. En estudios anteriores [48, 49, 50, 51, 52, 53, 54, 55] ya había una advertencia contra este tipo de "casi meritocracia", que mostraba la efectividad de estrategias alternativas basadas en elecciones aleatorias en las áreas de gestión, política y finanzas. Según este punto de vista, el modelo de TPU muestra cómo se puede aumentar el nivel mínimo de éxito para las personas más talentosas del mundo donde la suerte es importante, y el descubrimiento accidental a menudo conduce a logros importantes.

3.1. Descubrimiento accidental, innovación y estrategias efectivas de financiamiento.

El término "descubrimiento accidental" se usa ampliamente en referencias literarias a hechos históricos, lo que demuestra que los investigadores a menudo hacen descubrimientos inesperados y útiles por pura casualidad, cuando buscan otra cosa [61, 62]. Hay una larga lista de historias de descubrimientos realizados exclusivamente por coincidencia: desde la penicilina de Alexander Fleming hasta la radioactividad de Marie Curie, desde la radiación cósmica de fondo de microondas de los radioastrónomos Arno Penzias y Robert Woodrow Wilson hasta el grafeno Andrei Geim y Konstantin Novosyolov. Aquí hay un ejemplo más reciente: se descubrió por casualidad una red de canales llenos de líquido en el cuerpo humano, un órgano previamente desconocido que aparentemente promueve la propagación de las células cancerosas, durante una endoscopia simple [63]. Por lo tanto, muchas personas piensan que la investigación impulsada por la curiosidad siempre debe financiarse, ya que nadie puede saber de antemano o predecir a qué conducen [64].

¿Es posible cuantificar la importancia del descubrimiento aleatorio? ¿Cuáles son las formas más efectivas de simular el descubrimiento aleatorio? Puede tomar muchas formas diferentes, y es difícil de limitar y cuantificar. Es por eso que, hasta ahora, los estudios académicos han considerado un descubrimiento científico accidental, en su mayor parte, como un concepto filosófico. Pero los tiempos están cambiando. El Consejo Europeo de Investigación recientemente asignó una subvención de $ 1.7 millones al bioquímico Ohid Yakubu para calcular la importancia de un descubrimiento accidental en la ciencia [65]. Yakub descubrió que el descubrimiento aleatorio puede clasificarse en cuatro tipos básicos [66] y que puede haber factores importantes que influyen en su apariencia. Sus hallazgos parecen coincidir con ideas de investigaciones anteriores [67, 68, 69, 70, 71, 72], que sostienen que las estrategias generalmente aceptadas, claramente meritocráticas, que persiguen la superioridad y suplantan la diversidad parecen estar destinadas a perder. e ineficaz. La razón es que a priori rechazan la investigación que inicialmente parecía menos prometedora, pero que, gracias, en particular, a un descubrimiento aleatorio, a posteriori podría ser increíblemente innovadora.

Desde este punto de vista, queremos aplicar el modelo TPU, que naturalmente expresa suerte (y, en consecuencia, descubrimiento aleatorio) como un parámetro cuantitativo de la estrategia, para estudiar la efectividad de varios escenarios de financiamiento en esta subsección. En particular, en situaciones donde, como se mencionó anteriormente, una persona moderadamente talentosa pero afortunada es a menudo más exitosa que las personas más talentosas pero desafortunadas, es importante evaluar la efectividad de las estrategias financieras para la capacidad de mantener un nivel mínimo de éxito, incluso para Las personas más talentosas que se espera que traigan las ideas más innovadoras y progresivas.

Comenzando con los mismos parámetros iniciales que se usaron en la subsección 2.2, es decir N = 1000, m _T = 0.6, σ _T = 0.1, I = 80, δ _t = 6, C (0) = 10, NE = 500, p _L = 50% y 100 corridas de simulación, imaginemos que el capital de financiación total disponible F _{T se} distribuye periódicamente entre el individuo de acuerdo con diversos criterios. Por ejemplo, se pueden emitir finanzas:

1. Igualmente compartido (criterios igualitarios) para fomentar la diversidad de la investigación;
2. Solo un cierto porcentaje de los individuos más exitosos ("mejores") (criterio elitista), que anteriormente se llamaba la meritocracia "cercana", para la distribución de las finanzas entre las personas en función del rendimiento pasado.
3. Distribución "premium" entre una cierta proporción de los individuos más exitosos, y el resto, en pequeñas partes iguales, sobre el resto (criterio mixto);
4. Solo un cierto porcentaje de individuos seleccionados al azar (criterio aleatorio aleatorio).

Asumimos de manera realista que el capital total F _T se asignará cada 5 años, durante el período de 40 años de cada ejecución de simulación, de modo que F _T = 8 unidades de capital se distribuirán de vez en cuando . Mediante inyecciones periódicas de estas finanzas, pretendemos mantener un nivel mínimo de recursos de los agentes más talentosos. Por lo tanto, un buen indicador de la efectividad de la estrategia de financiamiento elegida puede ser el porcentaje P _T , promedio de 100 ejecuciones de simulación, para individuos con talento T > m _T + σ _T , cuyo éxito / capital total excede el nivel inicial, es decir, C _final> C (0).

Este porcentaje ya se ha calculado durante las ejecuciones de simulación presentadas en la sección 2.2. Demuestra que, en ausencia de financiación, los agentes más exitosos con un talento cercano al promedio lograron el mejor desempeño, mientras que el capital / éxito de las personas con más talento siempre sigue siendo extremadamente bajo. En particular, solo una parte de P _T0 ≈ 32% del número total de agentes con talento T > 0.7 fue capaz de lograr, en base a los resultados de la simulación, un capital / éxito superior al valor inicial. Por lo tanto, para comparar la efectividad de diferentes estrategias de financiamiento, se debe calcular el crecimiento del porcentaje promedio P _{T en} relación con P _T0aquellas personas con talento que han aumentado su capital inicial durante sus carreras. Definamos este crecimiento como P ^* _T = P _T - P _T0 . Este valor es un indicador bastante estable: lo verificamos repitiendo a partir de 100 simulaciones, la propagación de _los valores de P ^* _T se mantuvo por debajo del 2%. Finalmente, si calculamos la relación de P ^* _T con respecto al capital total distribuido entre todos los agentes durante 40 años, podemos obtener un índice de eficiencia E , que mide el crecimiento en el número de personas con talento suficientemente exitosas por unidad de capital invertido, definido como E = P ^* _T/ El F _T .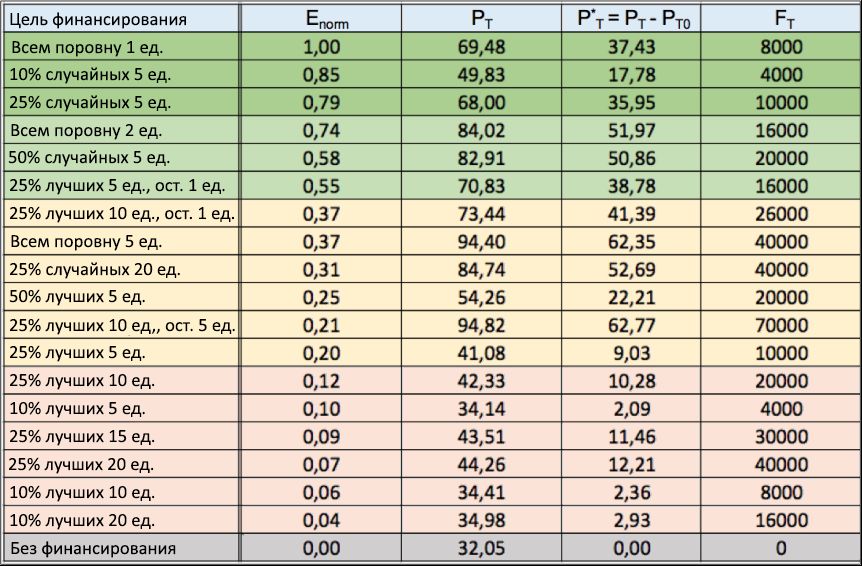


Figura 10: Tabla de estrategias de financiamiento. Se presentan varias estrategias para distribuir las finanzas para diversos fines (1 columna), con los resultados de la _norma E del índice de eficiencia normalizado (2 columnas), en orden descendente. Además, en la tercera y cuarta columnas, respectivamente, se muestran los valores de la participación P _{T de} personas exitosas con talento y el aumento neto en su número P ^* _T , en relación con el escenario "sin financiamiento", en promedio para 100 ejecuciones de simulación. Finalmente, la última columna muestra el capital total F _T invertido en cada ejecución.

En la tabla que se muestra en la Figura 10, mostramos el índice de desempeño (2da columna) obtenido para varias estrategias de distribución de financiamiento, cada una con su propio propósito financiero (1 columna), así como los valores correspondientes de P _T (3ra columna) y P ^* _T (cuarta columna). En la misma columna, en la última columna, se da el capital invertido total F _T para cada ejecución . Índice de Rendimiento E se normalizó con respecto a su valor máximo E _max , y todas las entradas (filas) en el orden de los valores criterio disminuir E _norma = E / E _max. Para el escenario con falta de financiación, por definición, _norma E = 0. Los mismos resultados de la _norma E se muestran en función de las estrategias de financiación adoptadas en forma de histograma en la Figura 11. Debido a la estabilidad estadística P _{T que} muestra desviaciones de menos del 2%, los resultados dados del índice de eficiencia E _{La norma} es estable.

Al considerar la tabla anterior y el histograma correspondiente de la Figura 11, resulta obvio que si el objetivo es recompensar a las personas más talentosas (aumentando así su nivel final de éxito), es mucho mejor asignar periódicamente (incluso una pequeña) cantidad de capital a todas las personas a la vez, en lugar de dar más capital a solo una pequeña parte de ellos, seleccionados de acuerdo con el nivel de éxito alcanzado en el momento de la distribución.


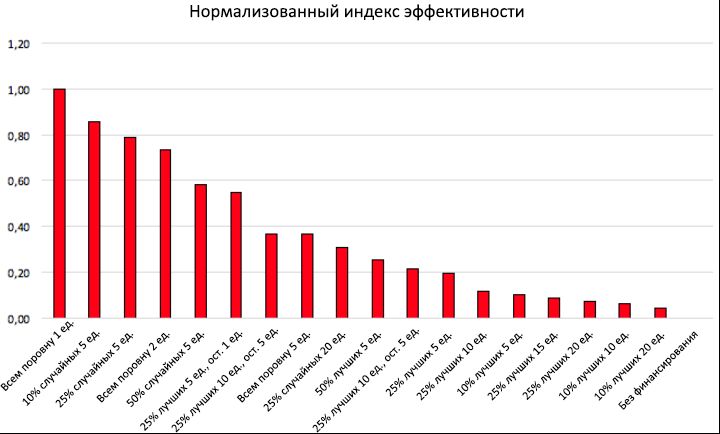Figura 11: Índice de rendimiento normalizado de algunas estrategias de financiación. Los valores de la _norma E del índice de eficiencia normalizado se dan en función de diversas estrategias de financiación. La figura muestra que, para aumentar el éxito de las personas más talentosas con C _final> C (0), es mucho más eficiente distribuir pequeñas cantidades de financiación entre muchas personas que financiar con otras formas más selectivas.

Por un lado, el histograma muestra que el criterio "igualitario", que asigna 1 unidad de capital a cada individuo cada 5 años, es la forma más eficiente de distribuir las finanzas, con la _norma E = 1 (es decir, E = E _max ): por relativamente pequeñas inversiones F _T por la cantidad de 8000 unidades, resulta duplicar el porcentaje de personas exitosas con talento, en comparación con el escenario "sin financiamiento", llevándolo de P _T0 = 32.05% a P _T= 69,48%, con un aumento neto de P ^* _T = 37,43. Cuando se considera aumentar el capital invertido total (por ejemplo, al establecer una cuota de nivelación de 2 o 5 unidades), esta estrategia también garantiza un aumento adicional en el porcentaje final de personas exitosas con talento (de 69.48% a 94.40%), pero la eficiencia normalizada en esto disminuye gradualmente, de la _norma E = 1 a la _norma E = 0.74, y luego a la _norma E = 0.37, respectivamente.

Por otro lado, las estrategias de "élite", distribuyendo cada 5 años por una gran cantidad de finanzas (5, 10, 15 o 20 unidades) solo entre los mejores 50%, 25% o incluso 10% de individuos exitosos, se encuentran en la parte inferior de la tabla, con_Norma E <0.25 en todos estos escenarios, el crecimiento neto P ^* _{T del} número total de personas exitosas con talento, en comparación con el escenario "sin financiamiento", sigue siendo extremadamente bajo (en casi todos los casos, menos del 20%), a menudo a pesar de una inversión mucho mayor capital, en comparación con una estrategia igualitaria similar. Estos resultados refuerzan la suposición de que tal enfoque obviamente no es muy meritocrático.

Vale la pena señalar que la adopción del criterio "mixto", es decir La distribución de la parte financiera "meritocrática" entre un cierto porcentaje de las personas más exitosas, por ejemplo, el 25%, con la distribución de las finanzas restantes en partes iguales a otras personas, da mejores resultados del índice de rendimiento en comparación con el enfoque "no muy meritocrático". Sin embargo, en términos de productividad, esta estrategia no puede alcanzar el criterio "igualitario". Como se ve claramente, por ejemplo, a partir de una comparación de la sexta y cuarta fila de la tabla de financiación: a pesar de la misma inversión total de 16,000 unidades, el valor de P _T obtenido con los criterios mixtos sigue siendo mucho más bajo que con el enfoque de nivelación (70.83% contra 84, 02%), que también se confirma por los valores correspondientes del índice de eficiencia E_norma (0.55 vs 0.74).

Si tenemos en cuenta los factores psicológicos (no modelados en este estudio), la estrategia mixta puede reconsiderarse en comparación con la igualitaria. De hecho, la recompensa de bonificación asignada a las personas más exitosas puede estimular una mayor adherencia entre todos los agentes, mientras que el resto distribuido equitativamente desempeñará un doble papel: a nivel individual, estimulará la diversidad y brindará nuevas oportunidades para que las personas talentosas sin éxito realicen su potencial, y el nivel general apoyará descubrimientos aleatorios, contribuyendo así al desarrollo de la investigación y la comunidad en general.

Mirando nuevamente la tabla de estrategias de financiamiento, vale la pena prestar atención a la increíblemente alta eficiencia de las estrategias aleatorias, que ocupan dos de las tres mejores posiciones en el resultado general. De ello se deduce que, por ejemplo, una recompensa periódica de 5 unidades de solo el 10% de los individuos seleccionados al azar, con una inversión total de solo 4,000 unidades, da un aumento neto de P ^* _T = 17.78%, que es más alto que casi todos los obtenidos mediante ecualización estrategias Además, aumentar al 25% la proporción de personas financiadas al azar y duplicar la inversión total (elevándolas a 10,000 unidades) da un crecimiento neto de P ^* _T= 35.95, comparable a la obtenida por la mejor estrategia de igualación, que ganó el primer lugar en la clasificación general. Llama la atención que este último resultado P ^* _T es aproximadamente cuatro veces el valor ( P ^* _T= 9.03%) obtenida usando el enfoque elitista (ver línea 12 de la tabla), que distribuyó exactamente el mismo capital (10,000 unidades) entre el mismo número de individuos (25% del total). Esto último confirma aún más que en entornos sociales y económicos complejos donde el azar juega un papel importante, la efectividad de otras estrategias basadas en elecciones aleatorias puede pasar fácilmente por alto las estrategias estándar basadas en el enfoque "casi meritocrático". Este fenómeno, contrario al sentido común, ya se ha observado en las áreas de administración, política y finanzas [48, 49, 50, 51, 52, 53, 54, 55], y por lo tanto encuentra otra confirmación en el contexto del estudio de financiamiento.

Para confirmar aún más los datos obtenidos, la Fig. 12 muestra los resultados de otra serie de simulaciones. A diferencia de las simulaciones anteriores, aquí la cantidad total de capital invertido en cada una de las 100 ejecuciones ahora se fija en F _T = 80,000, de modo que F _T / 8 = 10,000 unidades se distribuyen entre los agentes cada 5 años , de acuerdo con las mismas estrategias de financiamiento discutidas anteriormente . Mirando la tabla, vemos que los resultados de la estrategia igualitaria fueron nuevamente los más efectivos en términos de recompensar a las personas más talentosas, con una parte de P _TCerca del 100%. Esto es seguido por una estrategia aleatoria (con el 50% de las personas seleccionadas al azar para financiamiento), y luego mixta, en la que la mitad del capital se distribuye entre el 25% de las personas más exitosas y la otra parte, en partes iguales, entre otras personas. Por el contrario, todas las estrategias de élite se ubicaron nuevamente al final de la calificación, lo que confirma aún más la ineficiencia del enfoque "no muy meritocrático" en la recompensa del verdadero talento.


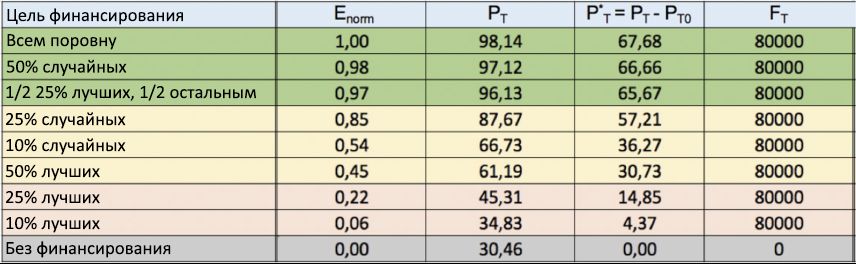Figura 12: Tabla de estrategias fijas de financiación financiera. Los índices de eficiencia normalizados obtenidos, la _norma E para varias estrategias de distribución de financiamiento (1ra columna) se muestran nuevamente en orden descendente, de arriba a abajo. A diferencia de la Figura 10, aquí el capital total invertido en cada ejecución se fija enF _T = 80,000 La estrategia de igualación nuevamente tomó el primer lugar.

Los resultados de las simulaciones del modelo TPU presentado en esta subsección llamaron la atención sobre la importancia de los factores externos (como, de hecho, políticas financieras efectivas) para aumentar las posibilidades de éxito para la mayoría de las personas talentosas que con demasiada frecuencia se ven castigadas por la coincidencia de eventos fallidos. En la siguiente subsección, examinamos en qué medida las nuevas oportunidades deberían provenir de los cambios ambientales, como el nivel de educación u otros incentivos derivados del entorno social en el que viven las personas o de dónde provienen.

3.2. Importancia del medio ambiente.

Para comenzar, analicemos el papel del nivel promedio de educación entre la población. En el marco del modelo TPU, se puede obtener cambiando los parámetros de la distribución normal del talento. En general, si suponemos que el talento y las habilidades de los individuos, cuando son estimulados, pueden ser más efectivos para aprovechar nuevas oportunidades, entonces el aumento de la mediana m _T o la desviación estándar del talento σ _T puede interpretarse como consecuencia de políticas dirigidas, respectivamente, a elevar el nivel promedio de educación o fortalecer la capacitación de las personas más talentosas.

En los dos diagramas de la Figura 13, presentamos el capital total / éxito acumulado por los mejores jugadores de cada una de las 100 carreras en función de su talento. Los parámetros dados corresponden a los utilizados en la subsección 2.2 ( N = 1000, I = 80, δ _t = 6, C (0) = 10, N _E = 500 y p _L = 50%), pero con diferentes momentos de distribución del talento . En particular, en el esquema (a) dejamos sin cambios m _T = 0.6, pero aumentamos σ _T = 0.2, mientras que en el esquema (b) hicimos lo contrario, dejando σ _T = 0.1 y elevando m_T = 0.7. En ambos casos, puede notar un cambio a la derecha de los picos de máximo éxito, pero con una diferencia en los detalles.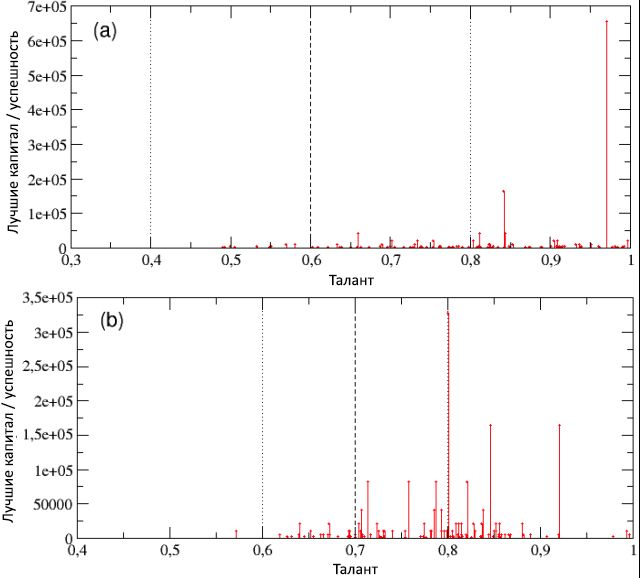


Figura 13: el capital total de los individuos más exitosos en cada una de las 100 carreras, presentado en función de su talento para poblaciones con diferentes parámetros de distribución de talento: (a) m _T = 0.6 y σ _T = 0.2 (que refleja el fortalecimiento de la capacitación capacitar a las personas más talentosas); (b) m _T = 0.7 y σ _T = 0.1 (que representa un aumento en el nivel promedio de educación). También se muestran los valores correspondientes de m _T y m _T ± σ _T., en forma de líneas discontinuas verticales y líneas punteadas, respectivamente.

De hecho, esto lleva al hecho de que un aumento en σ _T , a un valor constante de m _T , como se muestra en el diagrama (a), aumenta las posibilidades de que las personas más talentosas alcancen un éxito muy alto: el mejor actor ahora es un agente muy talentoso, con T = 0, 97, habiendo alcanzado un nivel increíble de capital / éxito C _mejor = 655360. Esto, por un lado, se puede evaluar positivamente, sin embargo, por otro lado, es un caso aislado y también, como contrapeso, hay una brecha creciente entre las personas desafortunadas y afortunadas. Mirando ahora el esquema (b), vemos que el aumento en m _Tsin cambiar σ _T da el mejor desempeño con C _mejor = 327680 y talento T = 0.8, seguido de dos más, con C = 163840 y, en consecuencia, T = 0.85 y T = 0.92. Esto sugiere que, en este caso, las posibilidades de que las personas más talentosas logren un éxito extremadamente alto aumentaron, pero al mismo tiempo, la brecha entre las personas desafortunadas y afortunadas era menor que antes.

Finalmente, en ambos ejemplos considerados, el valor promedio de capital / éxito de las 100 carreras más talentosas de personas aumentó en relación con el valor de C _mt ≈ 63 obtenido en la Subsección 2.2. En particular, tenemos C_mt ≈ 319 en el esquema (a) y C _mt ≈ 122 en el esquema (b), pero estos resultados son muy específicos para una serie particular de ejecuciones de simulación. Un parámetro más confiable para la expresión numérica de la efectividad de las políticas sociales estudiadas aquí es que nuevamente es el indicador P _T presentado en la subsección anterior, es decir. proporción promedio de individuos con talento T > m _T + σ _T y éxito total / capital C _final > 10, en relación con el número total de personas con talento T > m _T + σ _T (tenga en cuenta que aquí, en ambos casos,m _T + σ _T = 0.8). Entonces, obtuvimos P _T = 38% en el esquema (a) y P _T = 37.5% para el esquema (b), con un ligero aumento neto en relación con el valor de referencia P _T0 = 32% (obtenido para la distribución del talento en m _T = 0.6 y σ _T = 0.1).

Para resumir, nuestros resultados muestran que fortalecer la capacitación de las personas más talentosas o elevar el nivel promedio de educación conduce, como es de esperar, a algunos efectos positivos en el sistema social, ya que ambas políticas conducen a un aumento en la probabilidad de que las personas con talento se den cuenta de las oportunidades, les concedió suerte. Por otro lado, las mejoras en el porcentaje promedio de personas altamente talentosas que lograron alcanzar un buen nivel de éxito no parecen ser particularmente significativas para los dos escenarios analizados. Por lo tanto, el resultado de las políticas educativas relevantes parece estar limitado en gran medida a la ocurrencia de casos aislados de éxito excepcional.

Por supuesto, una vez que se estableció este nivel de educación, se hizo evidente que la abundancia de oportunidades que ofrece ese entorno social, es decir, El país donde alguien nació accidentalmente o decidió vivir es otro componente clave que puede influir en el rendimiento global del sistema.

En la Figura 14 presentamos resultados similares a los que eran visibles en la imagen anterior, pero para otra serie de simulaciones, con 100 corridas cada una, con los mismos parámetros establecidos que en la subsección 2.2 ( N = 1000, m _T = 0, 6, σ _T = 0.1, I = 80, C (0) = 10, N _E = 500) pero con diferentes porcentajes p _Leventos exitosos (recuerde que en la subsección 2.2 se tomó el porcentaje p _L = 50%). En el esquema (a), tomamos p _L = 80% para simular un entorno altamente estimulante lleno de oportunidades, típico de los países industrializados ricos como los Estados Unidos [26]. Por otro lado, en el esquema (b), un valor de p _L = 20% reproduce un escenario de un entorno mucho menos alentador, con un número extremadamente pequeño de posibilidades, como, por ejemplo, en los países del Tercer Mundo.


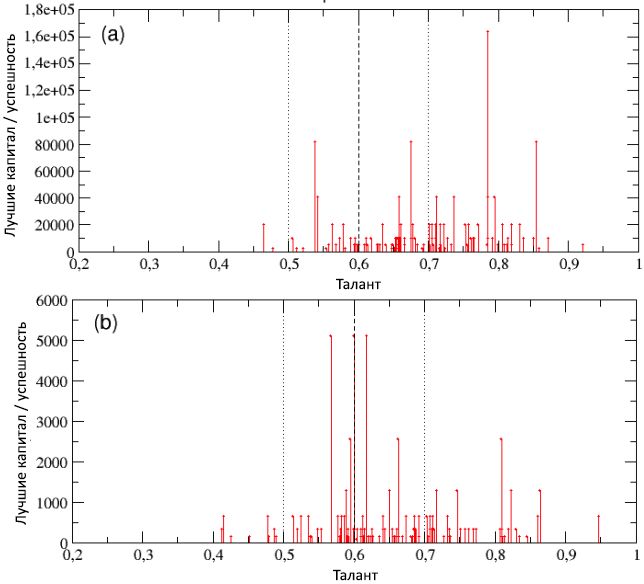Figura 14: el capital total de las personas más exitosas en cada una de las 100 carreras se muestra en función de su talento para las poblaciones que viven en entornos con diferentes porcentajes p _{L de} eventos exitosos: (a) p_L = 80%; (b) p _L = 20%. Además, las líneas punteadas verticales y punteadas marcan, respectivamente, los valores de m _T = 0.6 ym _T ± σ _T , con σ _T = 0.1.

Como se ve en ambos esquemas, la final del éxito / de capital individuos más afortunados que se muestran en función de su talento, son altamente dependientes de p _L .

En p _L = 80%, como en el esquema (a), varios agentes con talento medio-alto lograron mayoresniveles de éxito encomparación con el escenario p _L = 50%, con pico C_best = 163840. Por otro lado, el valor promedio de capital / éxito de las personas con más talento, C _mt ≈ 149, es bastante alto y, lo que es más importante, lo mismo se aplica al indicador P _T = 62.18% (que es aproximadamente el doble valor de referencia P _T0 = 32%), esto significa que, como se esperaba, las personas más talentosas se benefician de un mayor porcentaje de eventos exitosos.

Se obtuvieron resultados completamente diferentes con p _L = 20%. Por supuesto, como se puede ver en el esquema (b), el nivel general de éxito ahora es muy bajo en comparación con lo que se encontró en las simulaciones de la subsección 2.2, con un valor máximo de C _mejorque asciende a solo 5120 unidades, este es un rastro de la reducción de las desigualdades sociales, que es la consecuencia esperada de la igualdad de oportunidades para lograr el éxito. De acuerdo con estos resultados, el indicador P _T también alcanza un valor mínimo, con un porcentaje promedio de personas con talento que lograron aumentar su nivel inicial de éxito, igual a solo 8.75%.

Como resultado, en esta sección se demostró que el entorno alentador y la abundancia de oportunidades asociadas con la estrategia adecuada para asignar las finanzas y los recursos son factores importantes para lograr el potencial de las personas más talentosas, dándoles más oportunidades de lograr el éxito en comparación con los moderadamente dotados, pero más Suerte Desde un punto de vista a nivel macro, cualquier política que pueda influir en estos indicadores y apoyar a personas con talento dará como resultado el progreso colectivo y la innovación.

4. Observaciones finales

En este documento, comenzando con una serie de suposiciones extremadamente simples y racionales, presentamos un modelo de agente que fue capaz de medir cuantitativamente el papel del talento y la suerte en el éxito de las carreras de las personas. Las simulaciones mostraron que aunque el talento tiene una distribución gaussiana entre los agentes, la distribución final de éxito / capital, después de 40 años de vida laboral, sigue una función de poder de acuerdo con el principio de la ley de Pareto "80/20", que corresponde a la naturaleza de la distribución de la riqueza observada en el mundo real. Un resultado importante de las simulaciones es que los agentes más exitosos casi siempre no son los más talentosos, sino aquellos que están cerca del valor promedio de la distribución gaussiana del talento, un hecho ampliamente conocido que a menudo se encuentra en la literatura.El modelo muestra la importancia a menudo subestimada de los eventos exitosos para determinar el nivel final de éxito individual. Dado que las recompensas y los recursos generalmente se distribuyen a aquellos que ya han alcanzado un alto nivel de éxito, utilizados erróneamente como una medida de competencia / talento, esto lleva a un incentivo negativo, lo que provoca una falta de oportunidades para los talentos más altos. Nuestros resultados enfatizan los riesgos de un paradigma que llamamos una "casi meritocracia", que es incapaz de respetar y recompensar a las personas más competentes, ya que subestima el papel del azar entre los principales factores determinantes del éxito. En este sentido, se estudiaron varios escenarios diferentes para identificar las estrategias más efectivas que podrían equilibrar el papel impredecible de la suerte y dar más oportunidades y recursos a los más talentosos: la intención,cuál debería ser el objetivo principal de un enfoque verdaderamente meritocrático. También se demostró que estas estrategias son más beneficiosas para la comunidad en su conjunto, ya que conducen al crecimiento de varias ideas y perspectivas en la investigación, estimulando así la innovación.

Agradecimientos

Queremos agradecer a Robert Frank, Pavel Sobkowitz y Konstantino Tsallis por sus fructíferos debates y comentarios.

Bibliografia

1. Bak, P., Tang, C. y Wiesenfeld, K., Crítica autoorganizada. Phys. Rev. A , 38: 364 {374 (1988).
2. Barab´asi, A.-L., Albert, R., Aparición de escala en redes aleatorias, Science , vol. 286, número 5439, pp. 509 {512 (1999).
3. Newman, MEJ, Leyes de poder, distribuciones de Pareto y la ley de Zipf, Física contemporánea , 46 (5): 323 {351 (2005).
4. Tsallis, C., Introducción a la mecánica estadística no extensiva. Acercarse a un mundo complejo , Springer (2009).
5. Pareto, V., Cours d'Economique Politique , vol. 2 (1897).
6. Steindl, J., Random Processes and the Growth of Firms — A Study of the Pareto Law, Charles Griffin and Company , London (1965).
7. Atkinson, AB, Harrison, AJ, Distribution of Total Wealth in Britain, Cambridge University Press , Cambridge (1978).
8. Persky, J., Retrospectives: Pareto's law, Journal of Economic Perspectives 6, 181{192 (1992).
9. Klass, OS, Biham, O., Levy, M., Malcai, O., Solomon, S., The Forbes 400 and the Pareto wealth distribution, Economics Letters 90, 290{295 (2006).
10. Hardoon, D., An economy for the 99% , Oxfam GB, Oxfam House, John Smith Drive, Cowley, Oxford, OX4 2JY, UK (January 2017).
11. Bouchaud, J.-P., M´ezard, M., Wealth condensation in a simple model of economy, Physica A 282, 536{54 (2000).
12. Dragulescu, A. and Yakovenko, VM, Statistical mechanics of money, Eur. Phys. J. B 17, 723{729 (2000).
13. Chakraborti, A. and Chakrabarti, BK, Statistical mechanics of money: how saving propensity affects its distribution, Eur. Phys. J. B 17, 167{170 (2000).
14. Patriarca, M., Chakraborti, A., Germano, G., Influence of saving propensity on the power law tail of wealth distribution, Physica A 369(2), 723{736 (2006).
15. Scalas, E., Random exchange models and the distribution of wealth. European Physical Journal — Special Topics , 225. pp. 3293-3298. ISSN 1951{6355 (2016).
16. During, B., Georgiou, N. and Scalas, E., A stylised model for wealth distribution. In Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95{117. ISBN 9789811057045 (2017).
17. During, Bertram, Georgiou, Nicos and Scalas, Enrico (2017) A stylised model for wealth distribution. In: Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95-117. ISBN 9789811057045
18. Sinatra, R., Wang, D., Deville, P., Song, C. and Barab´asi, A.-L., Quantifying the evolution of individual scientific impact, Science 354, 6312 (2016).
19. Einav, L. and Yariv, L., What's in a Surname? The Effects of Surname Initials on Academic Success, Journal of Economic Perspective , Vol. 20, n. 1, p.175{188 (2006).
20. Ruocco, G., Daraio, C., Folli, V. and Leonetti, M., Bibliometric indicators: the origin of their log-normal distribution and why they are not a reliable proxy for an individual scholar's talent, Palgrave Communications 3:17064 doi: 10.1057/palcomms.2017.64 (2017).
21. Jurajda, S., Munich, D., Admission to Selective Schools, Alphabetically, Economics of Education Review , Vol. 29, n. 6, p.1100{1109 (2010).
22. Van Tilburg, WAP, Igou, ER, The impact of middle names: Middle name initials enhance evaluations of intellectual performance, European Journal of Social Psychology , Vol. 44, Issue 4, p.400{411 (2014).
23. Laham, SM, Koval, P., Alter, AL, The name-pronunciation effect: Why people like Mr. Smith more than Mr. Colquhoun, Journal of Experimental Social Psychology 48, p.752{756 (2012).
24. Silberzahn, R., Uhlmann, EL, It Pays to be Herr Kaiser: Germans with Noble-Sounding Last Names More Often Work as Managers, Psychological Science 24(12): 2437{44 (2013).
25. Coffey, B. and McLaughlin, P., From Lawyer to Judge: Advancement, Sex, and NameCalling. SSRN Electronic Journal , DOI10.2139/ssrn.1348280 (2009).
26. Milanovic, B., Global Inequality of Opportunity: How Much of Our Income Is Determined by Where We Live?, Review of Economics and Statistics , 97.2 (2015): 452{60.
27. Du, Q., Gao, H., Levi, MD, The relative-age effect and career success: Evidence from corporate CEOs, Economics Letters 117(3):660{662 (2012).
28. Deaner, RO, Lowen, A., Cobley, S., Born at the Wrong Time: Selection Bias in the NHL Draft. PLoS ONE 8(2): e57753 (2013).
29. Brooks, D., The Social Animal. The Hidden Sources of Love, Character, and Achievement, Random House , 424 pp. (2011).
30. Iacopini, I., Milojevic, S. and Latora, V., Network Dynamics of Innovation Processes, Physical Review Letters 120, 048301 (2018).
31. Tomasetti, C., Li, L., Vogelstein, B., Stem cell divisions, somatic mutations, cancer etiology, and cancer prevention, Science 355, 1330{1334 (2017).
32. Newgreen, DF et al., Differential Clonal Expansion in an Invading Cell Population: Clonal Advantage or Dumb Luck?, Cells Tissues Organs 203:105{113 (2017).
33. Snyder, RE and Ellner, SP, We Happy Few: Using Structured Population Models to Identify the Decisive Events in the Lives of Exceptional Individuals, The American Naturalist 188, no. 2 (2016): E28{E45.
34. Snyder, RE and Ellner, SP, Pluck or Luck: Does Trait Variation or Chance Drive Variation in Lifetime Reproductive Success?, The American Naturalist 191, no. 4 (2018): E90{E107.
35. .., . , , (2018).
36. .., . , (2018).
37. Mauboussin, MJ, The Success Equation: Untangling Skill and Luck in Business, Sports, and Investing, Harvard Business Review Press (2012).
38. .., . , (2019).
39. Watts, DJ, Everything Is Obvious: Once You Know the Answer , Crown Business (2011).
40. Salganik, MJ, Dodds PS, Watts DJ, Experimental Study of Inequality and Unpredictability in an Artificial Cultural Market, Science Vol.311 (2006)
41. Travis, M., Hofman, JM, Sharma, A., Anderson,. A., Watts, DJ, Exploring limits to prediction in complex social systems , Proceedings of the 25th ACM International World Wide Web Conference (2016) arXiv:1602.01013 [cs.SI]
42. Stewart, J., The Distribution of Talent, Marilyn Zurmuehlin Working Papers in Art Education 2 : 21-22 (1983).
43. Sinha, S. and Pan, RK, How a «Hit» is Born: The Emergence of Popularity from the Dynamics of Collective Choice, In Econophysics and Sociophysics: Trends and Perspectives (eds BK Chakrabarti, A. Chakraborti and A. Chatterjee), Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany. doi: 10.1002/9783527610006.ch15 (2006).
44. Fortin, J.-M., Curr, DJ, Big Science vs. Little Science: How Scientific Impact Scales with Funding, PLoS ONE 8(6): e65263 (2013).
45. Jacob, BA, Lefgren, L., The impact of research grant funding on scientific productivity, Journal of Public Economics 95 (2011) 1168{1177.
46. O'Boyle, JR. E. and Aguinis, H., The Best and the Rest: revisiting the norm of normality of individual performance, Personnel Psychology , 65: 79-119. doi:10.1111/j.1744-6570.2011.01239.x (2012).
47. Denrell, J. and Liu, C., Top performers are not the most impressive when extreme performance indicates unreliability, Proceedings of the National Academy of Sciences , 109(24):9331{9336 (2012).
48. Pluchino, A., Rapisarda, A., and Garofalo, C., The Peter principle revisited: A computational study, Physica A 389(3):467{472 (2010).
49. Pluchino, A., Garofalo, C., Rapisarda, A., Spagano, S. and Caserta, M., Accidental politicians: How randomly selected legislators can improve parliament efficiency, Physica A 390(21):3944{3954 (2011).
50. Pluchino, A., Rapisarda, A. and Garofalo, C., Efficient promotion strategies in hierarchical organizations, Physica A 390(20):3496{3511 (2011).
51. Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Reducing financial avalanches by random investments, Phys. Rev. E 88(6):062814 (2013).
52. Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Are random trading strategies more successful than technical ones, PLoS One 8(7):e68344 (2013)
53. Biondo, AE, Pluchino, A., Rapisarda, A., The beneficial role of random strategies in social and financial systems, J. Stat. Phys. 151(3-4):607{622 (2013).
54. Biondo, AE, Pluchino, A., Rapisarda, A., Micro and macro benefits of random investments in financial markets, Cont. Phys. 55(4):318{334 (2014).
55. Biondo, AE, Pluchino, A., Rapisarda, A., Modeling financial markets by self-organized criticality, Phys. Rev. E 92(4):042814 (2015).
56. Wilensky, U., NetLogo. ccl.northwestern.edu/netlogo . Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL (1999).
57. Merton, RK, The Matthew effect in science, Science 159, 56-63 (1968).
58. . ., , II: , https://www.hse.ru/data/033/314/1234/3_6_1Merto.pdf .
59. Bol, T., de Vaan, M. and van de Rijt, A., The Matthew effect in science funding, Proceedings of the National Academy of Sciences , DOI: 10.1073/pnas.1719557115 (2018).
60. Mongeon, P., Brodeur, C., Beaudry, C. et al., Concentration of research funding leads to decreasing marginal returns, Research Evaluation 25, 396{404 (2016).
61. Merton, RK, Barber, E., The Travels and Adventures of Serendipity , Princeton University Press, Princeton (2004).
62. Murayama, K. et al., Management of science, serendipity, and research performance, Research Policy 44 (4), 862{873 (2015).
63. Benias, PC et al., Structure and Distribution of an Unrecognized Interstitium in Human Tissues, Scientific Reports , vol. 8, 4947 (2018).
64. Flexner, A, The Usefulness of Useless Knowledge , Princeton University Press, Princeton (2017).
65. Lucky science. Scientists often herald the role of serendipity in research. A project in Britain aims to test the popular idea with evidence. , Nature Editorial, Vol.554, 1 February 2018.
66. Yaqub, O., Serendipity: Towards a taxonomy and a theory, Research Policy 47, 169{179 (2018).
67. Page, SE, The Diversity Bonus. How Great Teams Pay Off in the Knowledge Economy , Princeton University Press (2017).
68. Cimini, G., Gabrielli, A., Sylos Labini, F., The Scientific Competitiveness of Nations, PLoS ONE 9(12): e113470. doi.org/10.1371/journal.pone.0113470 (2014).
69. Curry, S., Let's move beyond the rhetoric: it's time to change how we judge research, Nature 554, 147 (2018).
70. Nicholson, JM and Ioannidis, JPA, Research grants: Conform and be funded, Nature 492, 34{36 (2012).
71. Bollen, J., Crandall, D., Junk, D. et al., An efficient system to fund science: from proposal review to peer-to-peer distributions, Scientometrics 110, 521{528 (2017).
72. Garner, HR, McIver, LJ and Waitzkin, MB, Research funding: Same work, twice the money?, Nature 493,599{601 (2013).

: Talent vs Luck: the role of randomness in success and failure