Árboles de búsqueda binaria equilibrada: implementación en Julia

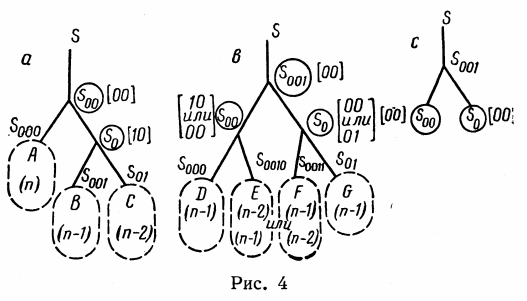
Ilustración del trabajo de G.M. Adelson-Welsky y E.M. Landis 1962

Los árboles de búsqueda son estructuras de datos para el almacenamiento ordenado y la búsqueda simple de artículos. Los árboles de búsqueda binarios son ampliamente utilizados, en los que cada nodo tiene solo dos hijos. En este artículo, consideramos dos métodos para organizar los árboles de búsqueda binarios: los algoritmos de Adelson-Welsky y Landis (árboles AVL) y los árboles AVL debilitados (árboles WAVL).

Comencemos con las definiciones. El árbol binario consta de nodos , cada nodo almacena un registro en forma de pares clave-valor (o, en el caso simple, solo valores) y no tiene más de dos hijos . Los nodos descendientes se distinguen por derecha e izquierda , y se cumple la condición para el orden de las claves: la clave del descendiente izquierdo ya no existe, y la derecha no es menor que la clave del nodo primario. Además, la información de servicio se puede almacenar (y generalmente se almacena) en nodos, por ejemplo, un enlace al nodo principal u otros datos. Los casos especiales son el nodo raíz desde el que entra el árbol y un nodo vacío que no almacena ninguna información. Los nodos en los que ambos descendientes están vacíos se llaman hojas de árbol. Un nodo con todos los descendientes forma un subárbol . Por lo tanto, cada nodo es la raíz de un subárbol o una hoja.

Esta definición le permite construir una estructura simple para almacenar nodos y el árbol en sí. Suponemos que un nodo vacío tiene el valor especial nothing tipo Nothing . Luego, en el nodo, es suficiente almacenar referencias a la descendencia derecha e izquierda y al padre. La estructura para almacenar el árbol contiene solo un enlace al nodo raíz.

 # K -   # V -    mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} end mutable struct BST{K, V} root::BSTNode{K,V} end 

En este caso, surge la pregunta de cómo representar un árbol vacío. Para hacer esto, utilizamos el enfoque del libro "Algorithms: Construction and Analysis" e insertamos como punto de entrada en el árbol, no una raíz, sino un nodo ficticio, que será su propio padre. Para crear dicho nodo, agregue constructores a la descripción de la estructura BSTNode:

 mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} #   function BSTNode{K,V}() where {K,V} node = new{K,V}() node.parent = node node.left = node.right = nothing return node end #    - function BSTNode{K,V}(key, value) where {K, V} node = new{K,V}() node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end BSTNode() = BSTNode{Any, Any}() #     ! struct BST{K, V} entry::BSTNode{K,V} BST{K,V}() where {K,V} = new{K,V}(BSTNode{K,V}()) end BST() = BST{Any, Any}() Base.isempty(bst::BST) = bst.entry.left == nothing 

En este caso, la estructura BST se puede hacer sin cambios, porque ya no será necesario cambiar el enlace al punto de entrada. Además, suponemos que el nodo raíz del árbol es inmediatamente el descendiente derecho e izquierdo del nodo de entrada.

La operación principal para la que se necesitan árboles de búsqueda es, naturalmente, la búsqueda de elementos. Como la clave del elemento secundario izquierdo ya no existe, y la clave correcta no es menor que la clave principal, el procedimiento de búsqueda de elementos se escribe de manera muy simple: a partir de la raíz del árbol, compare la clave de entrada con la clave del nodo actual; si las teclas coinciden, devolvemos el valor; de lo contrario, vaya al subárbol izquierdo o derecho, según el orden de las teclas. Si al mismo tiempo llegaron a un nodo vacío, no hay una clave en el árbol, arroje una excepción.

 #   Base.getindex()    #      tree[key] function Base.getindex(bst::BST{K,V}, key) where {K,V} key = convert(K, key) node = bst.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end 

La búsqueda de un elemento por clave, obviamente, toma tiempo O ( h ), donde h es la altura del árbol, es decir distancia máxima desde la raíz hasta la hoja. Es fácil calcular que un árbol binario de altura h puede contener como máximo 2 ^{h + 1} -1 nodos si está densamente poblado , es decir Todos los nodos, excepto, quizás, la capa muy extrema, tienen ambos descendientes. Además, está claro que cualquier secuencia de teclas por adelantado puede conducir a un árbol tan denso. Esto proporciona un comportamiento asintótico muy optimista de la búsqueda de un elemento en un árbol con su construcción óptima en el tiempo O (log ₂ N ), donde N es el número de elementos.

Naturalmente, el algoritmo para agregar un elemento al árbol de búsqueda debe construirse de tal manera que se cumpla la condición del orden de las claves. Escribamos una implementación ingenua de insertar un elemento por clave:

 #   Base.setindex!()    #       tree[key] = value function Base.setindex!(bst::BST{K,V}, val::SV, key::SK) where {K, V} key, value = convert(K, key), convert(V, val) parent = bst.entry.left #   -     if parent == nothing newnode.parent = bst.entry bst.entry.left = bst.entry.right = newnode return val end key_found = false while !key_found if key < parent.key if parent.left == nothing parent.left = BSTNode{K,V}(key, value) parent.left.parent = parent key_found = true else parent = parent.left end elseif key > parent.key if parent.right == nothing parent.right = BSTNode{K,V}(key, value) newnode.parent = parent key_found = true else parent = parent.right end else key_found = true parent.value = value end end return val end 

Desafortunadamente, la construcción ingenua del árbol dará la estructura deseada solo en datos de entrada aleatorios, pero en realidad a menudo están bastante estructurados. En el peor de los casos, si las claves entrantes están estrictamente ordenadas (al menos en orden ascendente, al menos en orden descendente), la construcción de árboles ingenuos enviará nuevos elementos todo el tiempo en una dirección, recogiendo, de hecho, una lista lineal. Es fácil adivinar que la inserción de elementos, que la búsqueda ocurrirá con dicha estructura durante O ( N ), lo que niega todos los esfuerzos para construir una estructura de datos compleja.

Conclusión: el árbol de búsqueda debe estar equilibrado durante la construcción, es decir alinee la altura del subárbol derecho e izquierdo en cada nodo. Hay varios enfoques para el equilibrio. Lo más simple es especificar un cierto número de operaciones de inserción o eliminación, después de lo cual se reequilibrará el árbol. En este caso, el árbol estará en un estado más bien "en ejecución" antes del balanceo, debido a que el balanceo tomará aproximadamente O ( N ) en el peor de los casos, pero las operaciones posteriores hasta cierto umbral de inserción / eliminación se realizarán en tiempo logarítmico. Otra opción es construir los algoritmos de inserción y eliminación de forma inmediata para que el árbol siempre permanezca equilibrado, lo que proporciona la complejidad de tiempo garantizada O (log ₂ N ) para cualquier operación.

Debido al hecho de que hay algoritmos en los que se permite que el árbol se "vuelva loco", pero después de eso, las operaciones se pueden llevar a cabo durante un tiempo bastante largo en un tiempo logarítmico, antes de que el árbol tenga que volver a un estado equilibrado durante mucho tiempo, se distingue el tiempo garantizado y amortizado de inserción / eliminación de un elemento. Para algunas implementaciones de operaciones con árboles de búsqueda binarios, la complejidad de insertar y eliminar O (log ₂ N ) está garantizada, para algunos se amortiza, con deterioro a O ( N ).

Algoritmo de Adelson-Welsky y Landis (AVL)

La primera implementación de un árbol de búsqueda binaria de equilibrio automático fue propuesta en 1962 por Adelson-Welsky y Landis. En la literatura moderna sobre las letras iniciales de los apellidos, esta estructura se llama árboles AVL . La estructura se describe mediante las siguientes propiedades:

1. Orden: para cualquier nodo, la clave en la parte superior del subárbol izquierdo es menor que la clave en la parte superior del subárbol derecho (si los descendientes no son nodos vacíos).
2. Aumento de altura: la altura del nodo padre es uno más que la altura máxima de sus descendientes. La altura de los nodos vacíos puede considerarse igual a cero.
3. Balance AVL: para cualquier nodo, las alturas de los subárboles derecho e izquierdo difieren en no más de 1.

De estas propiedades se deduce que la altura de todo el árbol es O (log ₂ N ), donde N es el número de registros almacenados en el árbol, lo que significa que el registro se busca en tiempo logarítmico. Para que la condición del equilibrio ABL permanezca después de cada inserción, cada inserción va acompañada de una operación de equilibrio . Para la implementación efectiva de esta operación, cada nodo necesita almacenar información de servicio. Para simplificar, simplemente mantenga la altura del nodo allí.

 mutable struct AVLNode{K,V} # ,       255 # (  10^38 ) height::UInt8 key::K value::V left::Union{Nothing, AVLNode{K,V}} right::Union{Nothing, AVLNode{K,V}} parent::AVLNode{K,V} #   function AVLNode{K,V}() where {K,V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing return node end #    - function AVLNode{K,V}(key::SK, value::SV) where {K, V, SK<:K, SV<:V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end avlheight(node::Union{Nothing,AVLNode}) = node == nothing ? 0 : Int(node.height) 

Insertar registro

La inserción básica se realiza de acuerdo con el algoritmo estándar: baje el árbol hacia abajo, busque dónde puede insertar un nuevo nodo e insertar. Vamos a escribir contenedores para obtener y reemplazar nodos secundarios utilizando los índices -1 y 1 en lugar de izquierda y derecha:

 function child(root::AVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function insert_child!(root::AVLNode{K,V}, newnode::Union{Nothing,AVLNode{K,V}}, side::Signed) where {K,V} newnode == nothing || (newnode.parent = root) if side == -1 root.left = newnode elseif side == 1 root.right = newnode else throw(ArgumentError("Expecting side=-1 for inserting node to the left or side=1 for inserting to the right")) end end 

A continuación, subimos al árbol y buscamos violaciones de las condiciones 2 y 3. A continuación, consideramos las opciones que pueden aparecer (en las figuras, el verde indica el nodo que cambió la altura, el nodo que se está procesando es su padre).

Caso 0
Después de la inserción, la altura del nodo se convirtió en la misma que la de la hermana, y 1 menor que la altura (antigua) del nodo padre.

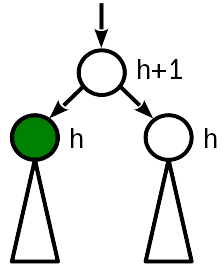
El mejor de los casos, no necesita tocar nada más. Arriba, también, ya no puedes mirar, porque nada cambiará allí.

Caso 1
Antes de la inserción, la altura del nodo era igual a la altura del nodo hermano. La inserción levanta la raíz del subárbol, y la altura del nodo se compara con la altura del padre.

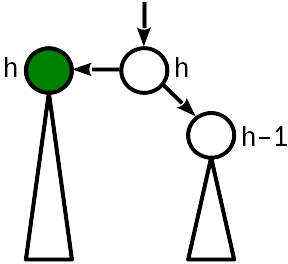
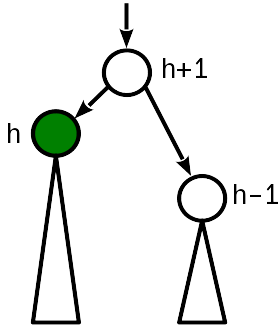
En este caso, es suficiente "elevar" el nodo primario, aumentando su altura en 1. Al mismo tiempo, debe continuar moviéndose a la raíz del árbol, ya que cambiar la altura del nodo primario podría conducir a la violación de la condición 2 un nivel más alto.

 fucntion promote!(nd::AVLNode, by::Integer=1) nd.height += by end fucntion demote!(nd::AVLNode, by::Integer=1) nd.height -= by end 

Caso 2

Después de la inserción, la diferencia de altura con el subárbol hermano se convirtió en 2, y el subárbol izquierdo "empujó" hacia arriba:

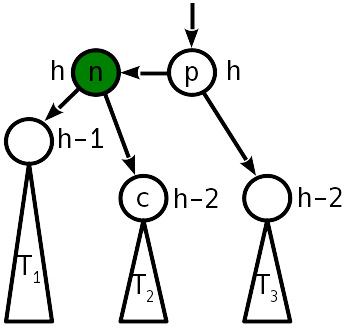
El problema se trata con una operación llamada "rotación simple" que transforma el árbol de la siguiente manera:

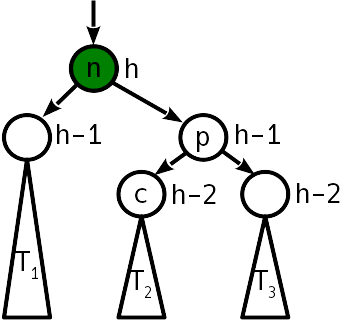
Un giro simple requiere 6 cambios de puntero.

Tenga en cuenta que en la proyección sobre el eje horizontal, el orden de los vértices n , p y los árboles T ₁ - T ₃ antes y después de la rotación sigue siendo el mismo. Este es el cumplimiento de la condición de pedido. Como puede ver, después de subir el árbol, ya no es necesario equilibrar.

 # pivot       function rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) p = pivot.parent g = p.parent p.height = avlheight(child(pivot, dir)) + 1 pivot.height = p.height + 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) c = child(pivot, dir) #  c  p insert_child!(p, c, -dir) #  p  pivot insert_child!(pivot, p, dir) pivot end 

Caso 3
Después de la inserción, la diferencia de altura con el subárbol hermano se convirtió en 2, y el subárbol derecho "empujó" hacia arriba:

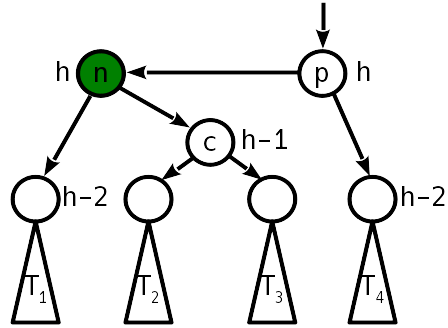
En este caso, un solo giro simple ya no ayudará, pero puede hacer un simple giro a la izquierda alrededor del descendiente derecho, lo que conducirá al caso 2, que ya está siendo tratado con un simple giro a la derecha.

Para reducir el número de "pesas" de nodos, se pueden combinar dos turnos en una sola operación, llamada turno grande o doble. Luego, en lugar de 12 cambios de punteros, solo se necesitarán 10. Como resultado de una doble rotación, el árbol toma la siguiente forma:

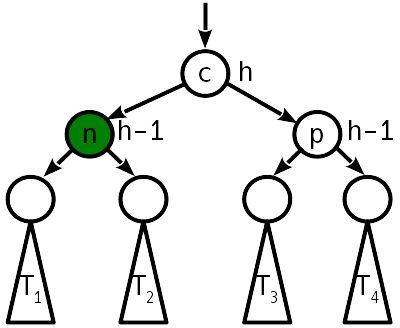
Como puede ver, después de un doble giro, tampoco es necesario equilibrar más el árbol.

 # pivot       funtion double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) #  n  pivot  t2  n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) #  p  pivot  t3  p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end 

Entonces, cuando inserta un registro en el árbol AVL, necesita O (log ₂ N ) cambios en la información sobre la altura de los nodos y no más de dos operaciones de rotación. Combina todo en una función de inserción. Diferirá de la inserción básica solo en que después de la inserción de un nuevo nodo, se fix_insertion!() la función fix_insertion!() , Que pasa del nodo recién insertado a la raíz, comprueba y, si es necesario, corrige el equilibrio.

 function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left #   -     if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 # true == 1, false == 0 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end 

La función fix_insertion!() Verifica la diferencia de altura entre dos nodos secundarios, comenzando desde el nodo principal desde el insertado. Si es igual a 1, estamos en el caso 1, debe elevar la altura del nodo e ir más alto. Si es cero, el árbol está equilibrado. Si es igual a 2, este es el caso 2 o 3, debe aplicar la rotación adecuada y el árbol llega a un estado equilibrado.

 #     -  , #   -  imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) #      0 - ..        while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 #       , # ..   dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end 

Eliminar registro

Quitarlo es un poco más difícil que insertarlo.

Para comenzar, considere la eliminación habitual de una entrada de un árbol de búsqueda binario.

1. Si el registro eliminado está en la hoja, entonces el registro simplemente se elimina, aquí todo es simple.
2. Si el registro eliminado está en un nodo que tiene un solo descendiente, este descendiente, junto con todo su subárbol, se coloca en el lugar del nodo remoto.
3. Si hay dos descendientes, entonces el elemento máximo se busca en el subárbol izquierdo, o el mínimo en el derecho, se extrae del árbol (por la propiedad del árbol de búsqueda, se garantiza que el nodo con el elemento máximo no tendrá un descendiente derecho y con un elemento mínimo a la izquierda, por lo que esta eliminación es fácil) y poner en lugar del registro eliminado.

Pero después de eso, el equilibrio del árbol puede verse alterado, por lo que debe subir desde el padre del nodo remoto y restaurarlo. Tenga en cuenta que al principio se garantiza que uno de los descendientes del padre en cuestión redujo la altura en 1. Teniendo esto en cuenta, debe tener en cuenta las opciones (los nodos que cambiaron la altura se muestran en rojo, el nodo procesado es el padre del rojo):

Caso 1
Cero desequilibrio. Entonces, antes de la eliminación, era 1 módulo, y ahora los nodos hijos son 2 más bajos que el padre.

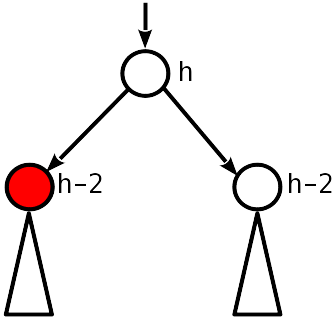
Debe bajar el nodo principal en 1 y continuar subiendo.

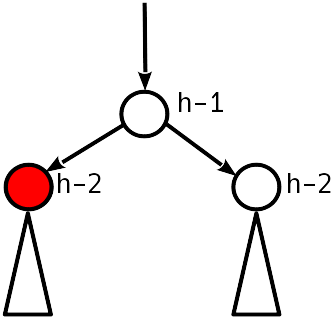
Caso 2
Desequilibrio 1 módulo.

La condición AVL está satisfecha, puede detenerse.

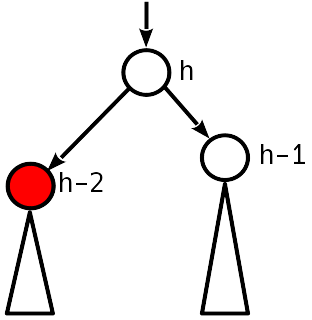
Caso 3
El desequilibrio 2 es módulo, el nodo hermano del descendente tiene un desequilibrio distinto de cero.

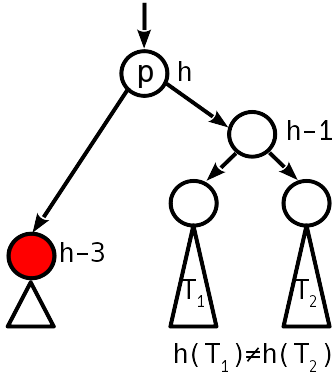
Restauramos el equilibrio por simple (si T _{1 es} menor que T ₂ ) o por doble rotación (de lo contrario), como se hizo durante la inserción. La altura del subárbol disminuye, es decir Una violación puede ocurrir sobre el árbol.

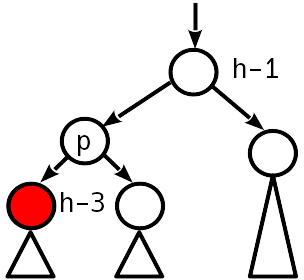
Caso 4
Módulo de desequilibrio 2, el nodo hermano tiene un desequilibrio cero.

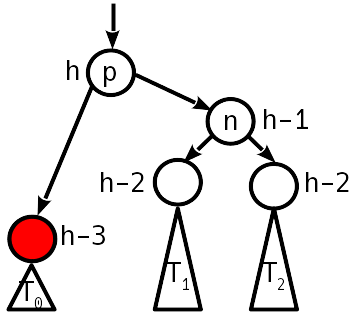
Una simple rotación restaura la condición de equilibrio, mientras que la altura del subárbol no cambia; dejamos de subir.

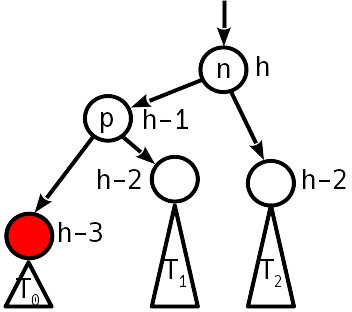
 function next_node(node::AVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::AVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::AVLNode) node = start skew = imbalance(node) while (node !== node.parent) && (abs(skew) != 1) if skew != 0 @assert abs(skew) == 2 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) < 2 if prev_skew == dir node = double_rotate!(child(n, dir), dir) else node = rotate!(n, dir) prev_skew != 0 || break end else node.height -= 1 end node = node.parent skew = imbalance(node) end end 

Ascenso y caída de árboles AVL

Una característica no muy agradable de los árboles AVL clásicos es la dificultad de eliminar un registro: una rotación puede "restablecer" todo el subárbol un nivel hacia abajo, luego, en el peor de los casos, la eliminación requiere rotaciones de árbol O (log ₂ N ), ¡cada vez que sube un nivel en fix_deletion!() .

Debido a este comportamiento asintótico no tan bueno, los árboles AVL dieron paso a los árboles rojo-negros que aparecieron en la década de 1970 y tienen una condición de equilibrio más débil: el camino desde la raíz hasta la hoja más alejada no es más del doble del camino desde la raíz hasta la hoja más cercana. Debido a esto, la altura de los árboles rojo-negros es, en el peor de los casos, 2log ₂ N versus 1.44log ₂ N para árboles AVL, pero eliminar un registro no requiere más de tres rotaciones simples. Por lo tanto, la búsqueda y la inserción debido a una mayor altura de árbol potencialmente pierden rendimiento, pero existe una ganancia potencial si las inserciones a menudo se intercalan con eliminaciones.

AVL contraataca

Resulta que el algoritmo "ideal" para construir árboles de búsqueda binarios debe garantizar una altura pequeña (al nivel del árbol AVL clásico) y un número constante de vueltas tanto al agregar o eliminar un registro. Esto aún no se ha inventado, pero en 2015 se publicó un trabajo que proponía una estructura que mejora las propiedades de los árboles AVL y rojo-negro. La idea se encuentra más cerca de los árboles AVL, pero la condición de equilibrio se relaja para permitir una eliminación más eficiente de los registros. Las propiedades de una estructura llamada “árbol AVL débil” (árbol AVL W (eak)) se formulan de la siguiente manera:

1. Orden: para cualquier nodo, la clave en la parte superior del subárbol izquierdo es más grande que en la parte superior del subárbol derecho que la clave del nodo en sí (si los descendientes no son nodos vacíos).
2. Rango ascendente. A cada nodo se le asigna un rango. El rango de todos los nodos vacíos es cero, el rango de las hojas es 1. El rango del nodo padre es estrictamente mayor que el rango del hijo.
3. Equilibrio ABL débil: el rango de un nodo difiere del rango de los nodos secundarios en no más de 2.

Resulta que dicha estructura incluye las propiedades de los árboles AVL clásicos y los árboles rojo-negros. En particular, si introducimos la condición de que ambos nodos hijos no pueden diferir del padre en rango en 2, obtenemos un árbol AVL regular, y el rango coincidirá exactamente con la altura del subárbol.

¡La belleza de los árboles SAVL es que un ligero debilitamiento de la condición AVL permite que el árbol se equilibre al eliminar un registro en no más de dos turnos! La estimación de la altura del árbol es h <min (1.44log ₂ M , 2log ₂ N ), donde N es el número de entradas en el árbol, M es el número de insertos, en comparación con h <2log ₂ N para árboles rojo-negros. , - , , .

- , . - .

.

-, "" "". , :

 mutable struct WAVLNode rank::UInt8 key::K value::V left::Union{Nothing, WAVLNode{K,V}} right::Union{Nothing, WAVLNode{K,V}} parent::WAVLNode{K,V} #   function WAVLNode{K,V}() where {K,V} node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing return node end #    - function WAVLNode{K,V}(key, value) where {K,V} key, value = convert(K, key), convert(V, value) node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end struct WAVLTree{K, V} entry::WAVLNode{K,V} WAVLTree{K,V}() where {K,V} = new{K,V}(WAVLNode{K,V}()) end function child(root::WAVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function Base.getindex(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) node = avlt.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end 

, -. : 1 , — , 0 ( ) 1 ( ). imbalance() , , .

 wavlrank(node::Union{Nothing,WAVLNode}) = node == nothing ? 0 : Int(node.rank) function imbalance(node::WAVLNode) rr, lr = wavlrank(node.right), wavlrank(node.left) skew = rr - lr diff = node.rank - max(rr, lr) skew, diff end 

, . , , , , -, - .

 # pivot       function rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) p = pivot.parent g = p.parent p.height = avlheight(child(pivot, dir)) + 1 pivot.height = p.height + 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) c = child(pivot, dir) #  c  p insert_child!(p, c, -dir) #  p  pivot insert_child!(pivot, p, dir) pivot end # pivot       function double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) #  n  pivot  t2  n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) #  p  pivot  t3  p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left #   -     if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end 

, — -. .

0
, ..:

1. 1, 1
2. 0, 2 , .
   .

1
2 ( 0, 2 ).
1 .

2
1, 2.

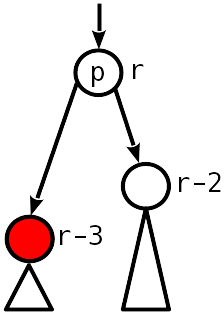
1, .

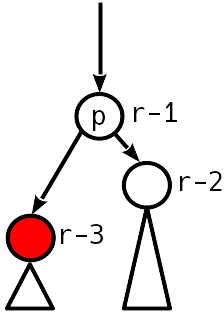
3
2 ( 1, .. ), 2 .

, . .

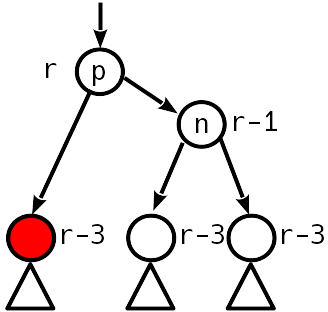
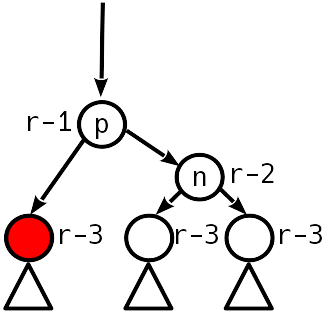
4

.

, , , .. .

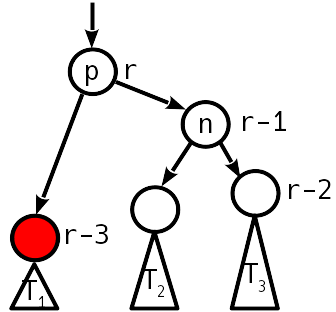
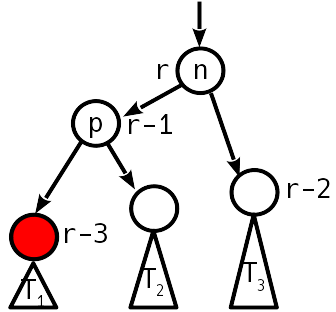
— T ₁ T ₂ , p 2, p 1.

5

.

, , .

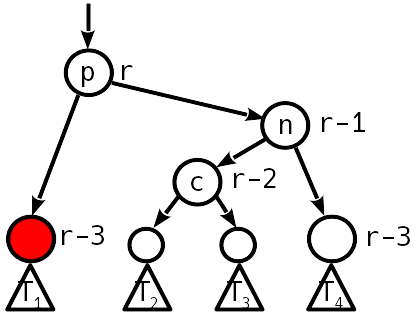
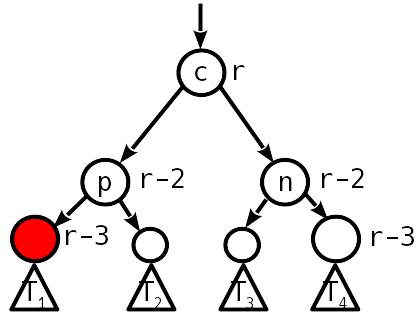
 function next_node(node::WAVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::WAVLNode) node = start skew, diff = imbalance(node) while (node !== node.parent) if skew == 0 if node.right == nothing node.rank = 1 else break end elseif abs(skew) == 1 if diff == 1 break else node.rank -= 1 end else dir = -skew ÷ 2 n = child(node, -dir) prev_skew, prev_diff = imbalance(n) if prev_diff == 2 @assert prev_skew == 0 n.rank -= 1 node.rank -= 1 elseif prev_skew == dir double_rotate!(child(n, dir), dir) break else rotate!(n, dir) break end end node = node.parent skew, diff = imbalance(node) end end 

-.

 julia> const wavl = WAVLTree{Int, Int}() julia> const avl = AVLTree{Int, Int}() julia> const dd = Dict{Int,Int}() julia> x = trues(1_000_000) #       ~  julia> for i = 1:1_000_000; dd[i] = avl[i] = wavl[i] = i * i; end julia> for i=1:500_000 k = rand(1:1_000_000) x[k] = false delete!(avl, k) delete!(wavl, k) delete!(dd, k) end # ,     julia> const y = Int[] julia> for i in eachindex(x); if x[i] push!(y, i); end; end julia> @btime let s = 0.0; for idx in y; s += dd[idx]; end; s; end 57.626 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += wavl[idx]; end; s; end 57.796 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += avl[idx]; end; s; end 53.884 ms (0 allocations: 0 bytes) 2.0238199367708794e17 

, , . , , - , -, .

— ?
— , . , , .

.

— , . n - . , , .. , .

*

— , " ", " ", " -", " ". , , -. . , .

*
** O (1), ...

, " — ". , . — ( ) , , , . .

*
** ,

Conclusión

() — , , , , , . — , .. , , .

Referencias

1. "-" nickme
2. Rank-Balanced Trees by Bernhard Haeupler, Siddhartha Sen, Robert E. Tarjan // ACM Transactions on Algorithms | June 2015, Vol 11(4) pdf
3. Goodrich MT, Tamassia R. Algorithm Design and Applications