Sobre el uso de métodos paramétricos de estimación espectral en radar: el método MUSIC. Adición al artículo.

Me encontré con un buen artículo sobre el método de estimación espectral, que es excelente para una señal corta de la suma de armónicos de bajo ruido. (-copia) Quizás mis comentarios ayudarán al lector a comprender la esencia del método. Lo que me molestó un poco fueron las capacidades implementadas de manera incompleta del método. El método se utiliza para el radar: para determinar rápidamente la dirección de las señales entrantes (ángulo θ) con el objetivo posterior de adaptación automática, debe entenderse, del sistema. Pero, el autor no produce una definición numérica de este ángulo (y esto es extraño en contexto), aunque esta definición es bastante posible. Tenemos solo gráficos hermosos, según los cuales, el sistema todavía necesita "gatear" y "gatear", determinando el número y la ubicación de los máximos, lo que no es del todo bueno.


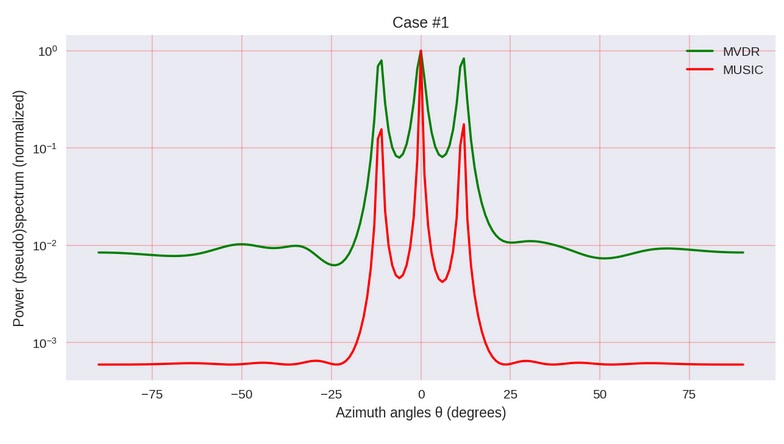Ilustración del autor del artículo mencionado.

"Declaración del problema"

En resumen: necesitamos determinar de alguna manera de dónde (a qué ángulo) proviene la señal de la antena enrejada. Luego, para ajustarlo en la dirección, pero esto ya no está en esta "canción".

"Modelado de la señal recibida"



(no es importante, aparentemente, el "símbolo" debe leerse en todas partes como una "señal")

Aquí, ten cuidado. El autor parece estar trabajando con una cierta señal compleja (espacial). Aunque X , sí, podría ser, como está escrito, una matriz de "amplitudes complejas" (dependiendo no de la coordenada, sino de la frecuencia espacial), pero, por ejemplo, XX ^H son "covarianzas" y no "densidades espectrales".

S es más similar a la matriz de "amplitudes complejas", con la ayuda de la cual se modelan los componentes armónicos (señal útil). Ni los ruidos aditivos, ni, al parecer, incluso los componentes armónicos son una señal analítica aquí. Aunque los armónicos, con reservas, están muy cerca de esto.



"# Fórmula general:
# sqrt (N0 / 2) * (G1 + jG2),
# donde G1 y G2 son procesos gaussianos independientes ".

Lo principal es de dónde proviene el componente imaginario de las mediciones reales, de alguna manera no está claro. Es posible, en principio, calcular la señal analítica.

Es posible que haya una "fuente" donde trabajaron con X real (señal recibida). Por ejemplo, el autor parece haber estado muy interesado en "hacer" que los espectros resultantes sean simétricos (incluso): en todos los casos considerados, las señales de prueba son dadas por las señales que llegan simétricamente a la izquierda y a la derecha.

"Términos"

Determinamos el rango de ángulos θ de llegada de la señal, en el que tiene sentido mirar. Es cierto, entonces creamos los gráficos de todos modos por alguna razón de +90 a -90 grados.

"Una pequeña teoría sobre el método en sí"

Además MUSIC se obtiene de la estimación autorregresiva (de las ecuaciones de Yule-Walker) casi por sí misma, en el caso en que la varianza del ruido blanco condicional es insignificante. Los resultados son casi iguales. La solución SLAE es incluso algo más económica que la búsqueda de vectores propios, pero, por cierto, por una serie de razones, la descomposición espectral de la matriz de covarianza con su condicionalidad pobre sería muy deseable de cualquier manera.

EVD, de hecho, es simplemente = "encontrar valores y vectores propios", y nada más. No es un algoritmo.

¿Por qué escribimos un "pseudo espectro?", Porque el espectro solo puede determinarse a partir de los vectores propios de la matriz de covarianza (correlación) solo hasta un factor de escala, es decir Los valores absolutos resultantes no tienen sentido. Pero necesitamos con precisión y solo la posición de los máximos.



- Esto es lo más interesante. Bueno, en primer lugar, U ₀ ya son vectores propios, solo para la matriz de covarianza, y "guardar" en su búsqueda fallará. Siguiente La búsqueda de soluciones dará lugar a la necesidad de determinar las raíces de la ecuación de potencia, que es absolutamente equivalente a otra descomposición espectral. El autor, aparentemente, confunde los valores propios de matrices completamente diferentes.

Pero ... lo principal ... ahora (!), Finalmente (!), Podríamos logaritmar las raíces y determinar numéricamente las complejas "impedancias" (polos modelo) (en la ecuación, esto es nuevamente θ, que no es muy bueno), que su parte imaginaria mostrará este mismo ángulo en el que llegó la señal. Es muy lamentable que el autor no lo haya hecho.

"Modelado"



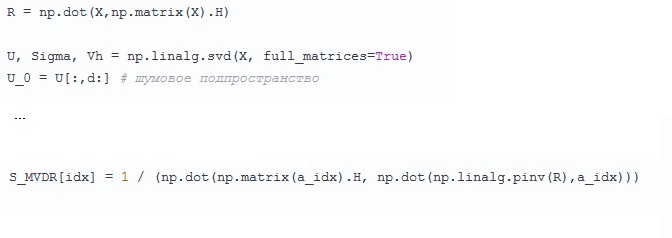
Aquí hay un poco alarmante: al principio ^se calculó la matriz de covarianza R = XX ^H , que por alguna razón se olvidó por un tiempo y comenzó de nuevo, descompuesta en números singulares y vectores X. Prometieron por texto buscar los valores propios y el vector R, que, por supuesto, es el mismo, pero como era más lógico, cuando R ya se ha encontrado. No está claro qué problema encontró el autor.

Recordamos R cuando evaluamos el espectro utilizando el método de dispersión mínima MVDR. Y aquí también es interesante: R , a juzgar por el guión, parece haberse invertido, de acuerdo con este método, de una manera clásica, sin ninguna SVD (pseudoinversión), aunque parece ser de bajo rango (altamente degenerado). Quiero decir, ¿nuestros ruidos son tan pequeños? Bueno tal vez.

Realmente confunde aquí eso. El tamaño del "subespacio de ruido" en el script parece estar asignado por el orden volitivo (igual a d). Pero en el caso real, no sabemos cuántos armónicos hay en la señal y cuántos ruidos. Era necesario analizar estos valores propios, cuáles de ellos son insignificantemente pequeños y cuáles no.

En general, el trabajo es muy interesante, y no solo para el radar. El método, creo, tiene un gran potencial, solo para este tipo de señales. El autor trabajó muy bien, y algunas inconsistencias molestas no son tan difíciles de solucionar. Y lo principal es complementar el artículo con el método RootMUSIC.