Si no está escribiendo un programa, no use un lenguaje de programación

Leslie Lamport es el autor del trabajo fundamental en computación distribuida, y también puede conocerlo por las letras La en La TeX - "Lamport TeX". Esta es la primera vez que presenta el concepto de consistencia consistente en 1979, y su artículo "Cómo hacer una computadora multiprocesador que ejecute correctamente programas multiproceso" ganó el Premio Dijkstra (más precisamente, en 2000 el premio se llamó de la manera antigua: "Premio de papel influyente PODC "). Hay un artículo en Wikipedia sobre él donde puedes obtener algunos enlaces más interesantes. Si está entusiasmado con la resolución de problemas en los eventos anteriores o los problemas de los generales bizantinos (BFT), entonces debe comprender que Lamport está detrás de todo esto.

Esta habrastatia es una traducción del informe de Leslie en el Heateberg Laureate Forum en 2018. La charla se centrará en los métodos formales utilizados en el desarrollo de sistemas complejos y críticos, como la sonda espacial Rosetta o los motores de Amazon Web Services. Ver este informe es imprescindible para la sesión de preguntas y respuestas que Leslie llevará a cabo en la Conferencia Hydra. Esta habrastatia puede ahorrarle una hora de tiempo viendo un video. Una vez completada esta introducción, pasamos la palabra al autor.

Érase una vez, Tony Hoar escribió: "Cada gran programa tiene un pequeño programa que intenta salir". Lo reformularía así: "En cada programa grande, hay un algoritmo que intenta salir". Sin embargo, no sé si Tony estaría de acuerdo con tal interpretación.

Considere, como ejemplo, el algoritmo euclidiano para encontrar el máximo divisor común de dos enteros positivos $$$(M, N)$ . En este algoritmo asignamos $$$x$ valor $$$M$ , $$$N$ - valor $$$y$ , y luego resta el más pequeño de estos valores del más grande, hasta que sean iguales. Significado de estos $$$x$ y $$$y$ y será el mayor factor común. ¿Cuál es la diferencia esencial entre este algoritmo y el programa que lo implementa? En dicho programa habrá muchas cosas de bajo nivel: $$$M$ y $$$N$ habrá un cierto tipo, BigInteger o algo así; será necesario determinar el comportamiento del programa si $$$M$ y $$$N$ no positivo y así sucesivamente. No existe una diferencia clara entre los algoritmos y los programas, pero en el nivel intuitivo sentimos la diferencia: los algoritmos son más abstractos, de nivel superior. Y, como dije, dentro de cada programa vive un algoritmo que intenta salir. Por lo general, estos no son los algoritmos que nos informaron en el curso de algoritmos. Como regla general, este es un algoritmo que es útil solo para este programa en particular. Muy a menudo, será mucho más complicado que los descritos en los libros. Tales algoritmos a menudo se llaman especificaciones. Y en la mayoría de los casos, este algoritmo no funciona, porque el programador no sospecha de su existencia. El hecho es que este algoritmo no se puede ver si su pensamiento se centra en el código, en los tipos, excepciones, bucles while y más, y no en las propiedades matemáticas de los números. Un programa escrito de esta manera es difícil de depurar, entonces, ¿qué significa depurar un algoritmo a nivel de código? Las herramientas de depuración están diseñadas para encontrar errores en el código y no en el algoritmo. Además, dicho programa será ineficaz porque, nuevamente, optimizará el algoritmo a nivel de código.

Como en casi cualquier otro campo de la ciencia y la tecnología, estos problemas pueden resolverse describiéndolos matemáticamente. Hay muchas formas de hacer esto, consideraremos las más útiles. Funciona con algoritmos secuenciales y paralelos (distribuidos). Este método consiste en describir la ejecución del algoritmo como una secuencia de estados, y cada estado como la asignación de propiedades a las variables. Por ejemplo, el algoritmo euclidiano se describe como una secuencia de los siguientes estados: primero, a x se le asigna el valor M (número 12) ey es el valor N (número 18). Luego restamos el valor más pequeño del más grande ( $$$x$ de $$$y$ ), lo que nos lleva al siguiente estado en el que ya estamos quitando $$$y$ de $$$x$ , y la ejecución del algoritmo se detiene en esto: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6], [x \ leftarrow 6, \ leftarrow 6]$ .

Llamamos un comportamiento de secuencia de estados y un par de estados consecutivos un paso. Entonces, cualquier algoritmo puede describirse mediante una variedad de comportamientos que representan todas las variantes posibles del algoritmo. Para cada M y N específicos, solo hay una realización, por lo tanto, un conjunto de un comportamiento es suficiente para describirlo. Los algoritmos más complejos, especialmente los paralelos, tienen muchos comportamientos.

Muchos comportamientos se describen, en primer lugar, por un predicado inicial para estados (un predicado es solo una función con un valor booleano); y, en segundo lugar, un predicado del siguiente estado para pares de estados. Algo de comportamiento $$$s_1, s_2, s_3 ...$ entra en muchos comportamientos solo si el predicado inicial es verdadero para $$$s_1$ , y los predicados del siguiente estado son verdaderos para cada paso $$$(s_i, s_ {i + 1})$ . Tratemos de describir el algoritmo euclidiano de esta manera. El predicado inicial aquí es: $$$(x = M) \ tierra (y = N)$ . Y el predicado del siguiente estado para pares de estados se describe mediante la siguiente fórmula:

No se alarme: solo hay seis líneas; es muy fácil resolverlas si hace esto en orden. En esta fórmula, las variables sin trazos se refieren al primer estado, y las variables con trazos son las mismas variables en el segundo estado.

Como puede ver, la primera línea dice que en el primer caso x es mayor que y en el primer estado. Después de un AND lógico, se afirma que el valor de x en el segundo estado es igual al valor de x en el primer estado menos el valor de y en el primer estado. Después de otro AND lógico, se afirma que el valor de y en el segundo estado es igual al valor de y en el primer estado. Todo esto significa que en el caso de que x sea mayor que y, el programa restará y de x y dejará y sin cambios. Las últimas tres líneas describen el caso cuando y es mayor que x. Tenga en cuenta que esta fórmula es falsa si x es igual a y. En este caso, no hay un estado siguiente y el comportamiento se detiene.

Entonces, acabamos de describir el algoritmo euclidiano en dos fórmulas matemáticas, y no tuvimos que meternos con ningún lenguaje de programación. ¿Qué podría ser más hermoso que estas dos fórmulas? Reemplácelos con una fórmula. Comportamiento $$$s_1, s_2, s_3 ...$ es la ejecución del algoritmo euclidiano solo si:

• $$$Init_E$ cierto para $$$s_1$ ,
• $$$Next_E$ cierto para cada paso $$$(s_i, s_ {i + 1})$ .

Esto se puede escribir como un predicado para comportamientos (lo llamaremos una propiedad) de la siguiente manera. La primera condición se puede expresar simplemente como $$$Init_E$ . Esto significa que interpretamos un predicado de estado como verdadero para el comportamiento solo si es verdadero para el primer estado. La segunda condición se escribe de la siguiente manera: $$$\ square Next_E$ . Un cuadrado significa la correspondencia entre los predicados de pares de estados y los predicados de comportamiento, es decir. $$$Next_E$ cierto para cada paso en el comportamiento. Como resultado, la fórmula se ve así: $$$Init_E \ land \ square Siguiente_E$ .

Entonces, escribimos el algoritmo euclidiano matemáticamente. En esencia, estas son simplemente definiciones o abreviaturas para $$$Init_E$ y $$$Next_E$ . Toda esta fórmula se vería así:

¿No es hermosa? Desafortunadamente, para la ciencia y la tecnología, la belleza no es un criterio determinante, pero sí significa que estamos en el camino correcto.

La propiedad que anotamos es cierta para algunos comportamientos solo si se cumplen las dos condiciones que acabamos de describir. En $$$M = 12$ y $$$N = 18$ son verdaderas para el siguiente comportamiento: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6], [x \ leftarrow 6, \ leftarrow 6]$ . Pero estas condiciones también se cumplen para versiones más cortas del mismo comportamiento: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6]$ . Y no debemos tenerlos en cuenta, ya que estos son solo pasos separados del comportamiento que ya hemos tenido en cuenta. Hay una forma obvia de deshacerse de ellos: simplemente ignore los comportamientos que terminan en un estado para el que al menos un próximo paso es posible. Pero este no es el enfoque correcto, necesitamos una solución más general. Además, esta condición no siempre funciona.

Una discusión sobre este problema nos lleva a los conceptos de seguridad y actividad. La propiedad de seguridad indica qué eventos son válidos. Por ejemplo, el algoritmo puede devolver el valor correcto. La propiedad de actividad indica qué eventos deberían ocurrir tarde o temprano. Por ejemplo, un algoritmo debería devolver algún valor tarde o temprano. Para el algoritmo euclidiano, la propiedad de seguridad es la siguiente: $$$Init_E \ land \ square Siguiente_E$ . Se debe agregar una propiedad de actividad para evitar paradas prematuras: $$$Init_E \ land \ square Siguiente_E \ land L$ . En los lenguajes de programación, en el mejor de los casos, existe una definición primitiva de actividad. En la mayoría de los casos, ni siquiera se menciona la actividad, simplemente se da a entender que el siguiente paso en el programa debe suceder. Y para agregar esta propiedad, necesita un código bastante complejo. Matemáticamente, es muy fácil expresar actividad (solo se necesita ese cuadrado para esto), pero, desafortunadamente, no tengo tiempo para esto, tendremos que limitar nuestra discusión a la seguridad.

Una pequeña digresión solo para matemáticos: cada propiedad es un conjunto de comportamientos para los cuales esta propiedad es verdadera. Para cada conjunto de secuencias, existe una topología natural que crea la siguiente función de distancia:

$$$s = 17, \ sqrt {2}, -2, \ pi, 10, 1/2 \\ t = 17, \ sqrt {2}, -2, e, 10, 1/$

La distancia entre estas dos funciones es de ¼, ya que la primera diferencia entre ellas está en el cuarto elemento. En consecuencia, cuanto más larga sea la porción en la que estas secuencias son idénticas, más cercanas estarán entre sí. Esta función en sí misma no es tan interesante, pero crea una topología muy interesante. En esta topología, las propiedades de seguridad son conjuntos cerrados y las propiedades de actividad son conjuntos densos. En topología, uno de los teoremas fundamentales establece que cada conjunto es la intersección de un conjunto cerrado y un conjunto denso. Si recordamos que las propiedades son conjuntos de comportamientos, de este teorema se deduce que cada propiedad es una conjunción de una propiedad de seguridad y una propiedad de actividad. Esta es una conclusión que también será interesante para los programadores.

La corrección parcial significa que el programa solo puede detenerse si da la respuesta correcta. La corrección parcial del algoritmo euclidiano dice que si completa la ejecución, entonces $$$x = MCD (M, N)$ . Y nuestro algoritmo completa la ejecución si $$$x = y$ . En otras palabras $$$(x = y) \ Rightarrow (x = MCD (M, N))$ . La corrección parcial de este algoritmo significa que esta fórmula es verdadera para todos los estados de comportamiento. Agregue un símbolo a su comienzo $$$\ cuadrado$ que significa "para todos los pasos". Como puede ver, no hay variables con un trazo en la fórmula, por lo que su verdad depende del primer estado en cada paso. Y si algo es cierto para el primer estado de cada paso, entonces esta afirmación es verdadera para todos los estados. La corrección parcial del algoritmo euclidiano se satisface con cualquier comportamiento aceptable para el algoritmo. Como hemos visto, el comportamiento es permisible si la fórmula que se acaba de dar es verdadera. Cuando decimos que una propiedad está satisfecha, simplemente significa que esta propiedad se deriva de alguna fórmula. ¿No es maravilloso? Aquí esta:

$$$Init_E \ land \ square Next_E \ Rightarrow \ square ((x = y) \ Rightarrow (x = MCD (M, N)))$

Pasamos a la invariancia. El cuadrado entre paréntesis después de que se llama la propiedad de invariancia :

$$$Init_E \ land \ square Next_E \ Rightarrow \ color {red} {\ square ((x = y) \ Rightarrow (x = GCD (M, N)))}$

El valor encerrado entre paréntesis después del cuadrado se llama invariante :

$$$Init_E \ land \ square Next_E \ Rightarrow \ square (\ color {red} {(x = y) \ Rightarrow (x = MCD (M, N))})$

¿Cómo probar la invariancia? Para probar $$$Init_E \ land \ square Next_E \ Rightarrow \ square I_E$ , debes probar eso para cualquier comportamiento $$$s_1, s_2, s_3 ...$ la consecuencia $$$Init_E \ land \ square Siguiente_E$ es verdad $$$I_e$ para cualquier condición $$$s_j$ . Podemos probar esto por inducción, para esto necesitamos probar lo siguiente:

1. de $$$Init_E \ land \ square Siguiente_E$ se sigue que $$$I_e$ cierto para el estado $$$s_1$ ;
2. de $$$Init_E \ land \ square Siguiente_E$ se deduce que si $$$I_e$ cierto para el estado $$$s_j$ entonces también
   cierto para el estado $$$s_ {j + 1}$ .

Primero tenemos que demostrar que $$$Init_E$ implica $$$I_e$ . Porque la fórmula afirma que $$$Init_E$ cierto para el primer estado, esto significa que $$$I_e$ cierto para el primer estado. Además, cuando $$$Next_E$ cierto para cualquier paso, y $$$I_e$ fiel a $$$s_j$ , $$$I_e$ cierto para $$$s_ {j + 1}$ porque $$$\ square Next_E$ significa que $$$Next_E$ cierto para cualquier par de estados. Esto se escribe así: $$$Next_E \ land I_E \ Rightarrow I'_E$ donde $$$I'_E$ Es eso $$$I_e$ para todas las variables con un trazo.

Un invariante que cumple con las dos condiciones que acabamos de probar se llama invariante inductivo . La corrección parcial no es inductiva. Para probar su invariancia, necesita encontrar la invariante inductiva que lo implica. En nuestro caso, la invariante inductiva será la siguiente: $$$MCD (x, y) = MCD (M, N)$ .

Cada acción posterior del algoritmo depende de su estado actual y no de acciones pasadas. El algoritmo satisface la propiedad de seguridad, ya que el invariante inductivo se conserva en él. El algoritmo euclidiano puede calcular el denominador común más grande (es decir, no se detiene hasta que se alcanza) debido al hecho de que tiene una invariante $$$MCD (x, y) = MCD (M, N)$ . Para comprender el algoritmo, debe conocer su invariante inductivo. Si estudiaste la verificación de programas, entonces sabes que la prueba de invariante que acabas de dar no es más que un método para probar la corrección parcial de los programas de Floyd-Hoare secuenciales. También es posible que haya oído hablar del método Hoviki - Gris , que es la extensión del método Floyd-Hoar a programas paralelos. En ambos casos, la invariante inductiva se escribe utilizando la anotación del programa. Y si haces esto con la ayuda de las matemáticas, y no con un lenguaje de programación, esto se hace extremadamente simple. Eso es lo que se encuentra en el corazón del método Hoviki Gris. La matemática hace que los fenómenos complejos sean mucho más accesibles para la comprensión, aunque los fenómenos en sí mismos, por supuesto, no serán más simples.

Eche un vistazo más de cerca a las fórmulas. Si en matemáticas escribimos una fórmula con variables $$$x$ y $$$y$ , esto no significa que no existan otras variables. Puedes agregar otra ecuación en la cual $$$y$ colocado en relación a $$$z$ , no cambiará nada. Solo la fórmula no dice nada sobre ninguna otra variable. Ya dije que un estado es una asignación de valores a variables, ahora puede agregar a esto: con todas las variables posibles, comenzando $$$x$ y $$$y$ y terminando con la población de Irán. Debo confesar: cuando dije que la fórmula $$$Init_E \ land \ square Siguiente_E$ describe el algoritmo euclidiano, mentí. En realidad, describe un universo en el que los significados $$$x$ y $$$y$ representar la ejecución del algoritmo euclidiano. La segunda parte de la fórmula ( $$$\ square Next_E$ ) afirma que cada paso cambia $$$x$ o $$$y$ . En otras palabras, describe un universo en el que la población de Irán solo puede cambiar si el significado ha cambiado. $$$x$ o $$$y$ . De ello se deduce que en Irán nadie puede nacer después de que se complete la ejecución del algoritmo euclidiano. Obviamente, esto no es así. Este error puede corregirse si tenemos pasos válidos para los cuales $$$x$ y $$$y$ permanecer sin cambios. Por lo tanto, necesitamos agregar una parte más a nuestra fórmula: $$$Init_E \ land \ square (Next_E \ lor (x '= x) \ land (y' = y))$ . Por brevedad, lo escribimos así: $$$Init_E \ land \ square [Siguiente_E] _ {<x, y>}$ . Esta fórmula describe un universo que contiene el algoritmo euclidiano. Se deben hacer los mismos cambios en la prueba de la invariante:

• Probamos: $$$Init_E \ land \ color {red} {\ square [Next_E] _ {<x, y>}} \ Rightarrow \ square I_E$
• Con la ayuda de:
  
  1. $$$Init_E \ Rightarrow I_E$
  2. $$$\ color {rojo} {\ square [Siguiente_E] _ {<x, y>}} \ land I_E \ Rightarrow I'_E$

Este cambio es responsable de la seguridad del algoritmo euclidiano, ya que ahora son posibles los comportamientos en los que los valores $$$x$ y $$$y$ no cambies Estos comportamientos deben eliminarse utilizando la propiedad de actividad. Esto es bastante simple, pero no voy a hablar de eso ahora.

Habla sobre la implementación. Supongamos que tenemos algún tipo de máquina que implementa el algoritmo euclidiano como una computadora. Representa los números como matrices de palabras de 32 bits. Para operaciones simples de suma y resta, necesita muchos pasos, como una computadora. Si todavía no toca la actividad, también podemos imaginar una máquina de este tipo con la fórmula $$$Init_ {ME} \ land \ square [Siguiente_ {ME}] _ {<...>}$ . ¿Qué queremos decir cuando decimos que la máquina euclidiana implementa el algoritmo euclidiano? Esto significa que la siguiente fórmula es correcta:

No se alarme, ahora lo examinaremos en orden. Dice que nuestra máquina satisface alguna propiedad ( $$$\ Rightarrow$ ) Esta propiedad es la fórmula euclidiana. $$$(Init_E \ land \ square [Siguiente_E] _ {<x, y>}$ , los puntos son expresiones que contienen variables de máquina euclidianas, y $$$CON$ Es una sustitución. En otras palabras, la segunda línea es la fórmula euclidiana en la que $$$x$ y $$$y$ reemplazado por puntos. En matemáticas, no existe una notación universalmente aceptada para la sustitución, así que tuve que proponerla yo mismo. Esencialmente, la fórmula euclidiana ( $$$Init_E \ land \ square [Siguiente_E] _ {<x, y>}$ ) Es una abreviatura de la fórmula:

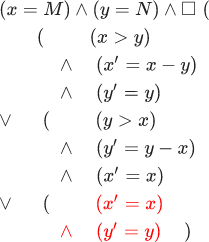
Parte resaltada en rojo de la fórmula, permitiendo $$$x$ y $$$y$ en $$$(Init_E \ land \ square [Next_E] _ {\ color {red} {<x, y>}}$ permanece igual

La expresión descrita establece no solo que la máquina implementa el algoritmo euclidiano, sino que también lo hace teniendo en cuenta las sustituciones especificadas. Si solo toma un par de programas y dice que las variables de estos programas están relacionadas con $$$x$ y $$$y$ - No tiene sentido decir que todo esto "implementa el algoritmo euclidiano". Es necesario indicar exactamente cómo se implementará el algoritmo, por qué, después de todas las permutaciones, la fórmula se hará realidad. Ahora no tengo tiempo para mostrar que la definición descrita anteriormente es correcta, debe aceptar mi palabra. Pero tú, creo, ya has apreciado lo simple y elegante que es. La matemática es realmente hermosa: con ella pudimos determinar qué significa que un algoritmo implemente otro.

Para probar esto, es necesario encontrar un invariante adecuado $$$I_ {ME}$ Autos euclidianos. Para hacer esto, se deben cumplir las siguientes condiciones:

1. $$$Init_ {ME} \ Rightarrow (Init_E, WITH \ thinspace x \ leftarrow ..., y \ leftarrow ...)$
2. $$$I_ {ME} \ land [Next_ {ME}] _ {<...>} \ Rightarrow ([Next_E] _ {<x, y>}, WITH \ thinspace x \ leftarrow ..., y \ leftarrow. ..)$

No profundizaremos en ellos ahora, solo prestemos atención al hecho de que se trata de fórmulas matemáticas ordinarias, aunque no las más simples. Invariante $$$I_ {ME}$ explica por qué la máquina euclidiana implementa el algoritmo euclidiano. Implementación significa sustituir expresiones por variables. Esta es una operación matemática muy común. Pero en el programa, tal sustitución no se puede realizar. No puede sustituir a + b en lugar de x en la expresión de asignación x = … , dicho registro no tendrá sentido. Entonces, ¿cómo determinar que un programa implementa otro? Si solo piensa en términos de programación, esto no es posible. En el mejor de los casos, puede encontrar alguna definición complicada, pero una forma mucho mejor es traducir los programas a fórmulas matemáticas y usar la definición que proporcioné anteriormente. Traducir un programa a una fórmula matemática es darle semántica al programa. Si la máquina euclidiana es un programa, y $$$Init_ {ME} \ land \ square [Siguiente_ {ME}] _ {<...>}$ - su notación matemática, entonces $$$(Init_E \ land \ square [Next_E] _ {<x, y>}, WITH \ thinspace x \ leftarrow ..., y \ leftarrow ...)$ nos muestra que esto significa que "el programa implementa el algoritmo euclidiano". Los lenguajes de programación son muy complejos, por lo que esta traducción del programa a un lenguaje matemático también es complicada, por lo que en la práctica no hacemos eso. Simplemente, los lenguajes de programación no están diseñados para escribir algoritmos en ellos. , , , : , x y , . , , , .

- : , , , . , . — . . , . , — , . :

. $$$DecrementX$ :

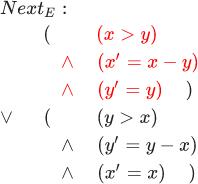
— $$$DecrementY$ :

, :

.

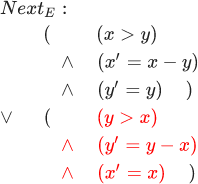
. Rosetta — , . Virtuoso. . TLA+, . , , . , (Eric Verhulst), . , TLA+, : « TLA+ . - C. TLA+ Virtuoso». . . , , , . . TLA+. , .

. Communications of the ACM ] , - Amazon . Amazon Web Services — , Amazon. , — TLA+. . -, , . , , . -, , . , — , , . -, , Amazon , . , 10% TLA+.

— Microsoft. TLA+ 2004 . 2015 TLA+, . . Amazon Web Services. Microsoft , , . : « , ». , Microsoft - . : « ». 2016-17 . TLA+, 150 , Azure ( Microsoft). Azure 2018 , , . : « , . , ». , , . - : , . , , .

, TLA+ . , TLA+, TLA+ Azure, , TLA+. , . , TLA+ , . Microsoft Cosmos DB, , . , . TLA+, , , TLA+.

TLA+ — . . TLA+ . , , . TLA+ , . : TLA+ , .

, . , , . , . Amazon Microsoft , . , .

, . — , . , Hydra 2019, 11-12 2019 -. .