😽 🧔🏽 👵🏼 Filtrado lineal óptimo: desde descenso de gradiente hasta filtros adaptativos 🖖🏼 🏆 ↩️

Desarrollando el tema de los resúmenes en la especialidad de maestría "Procesamiento de comunicación y señal" (TU Ilmenau), me gustaría continuar uno de los temas principales del curso "Procesamiento de señal adaptativo y de matriz" . A saber, los conceptos básicos del filtrado adaptativo.

Para quién se escribió este artículo por primera vez:

1) para una hermandad estudiantil de una especialidad nativa ;
2) para los docentes que preparan seminarios prácticos, pero que aún no han decidido las herramientas: a continuación se muestran ejemplos en python y Matlab / Octave ;
3) para cualquier persona interesada en el tema del filtrado.

Lo que se puede encontrar debajo del corte:

1) información de la teoría, que traté de organizar de la manera más concisa posible, pero me parece informativa;
2) ejemplos del uso de filtros: en particular, como parte del ecualizador para el conjunto de antenas;
3) enlaces a literatura básica y bibliotecas abiertas (en python), que pueden ser útiles para la investigación.

En general, bienvenido y clasifiquemos todo por puntos.

La persona pensativa en la foto es familiar para muchos, creo, Norbert Wiener. En su mayor parte, estudiaremos el filtro de su nombre. Sin embargo, uno no puede dejar de mencionar a nuestro compatriota: Andrei Nikolaevich Kolmogorov, cuyo artículo de 1941 también hizo una contribución significativa al desarrollo de la teoría de filtrado óptima, que incluso en fuentes en inglés se llama la teoría de filtrado de Kolmogorov-Wiener .

¿Qué estamos considerando?

Hoy estamos considerando un filtro clásico con una respuesta de impulso finita (FIR, respuesta de impulso finita), que puede describirse mediante el siguiente circuito simple (Fig. 1).

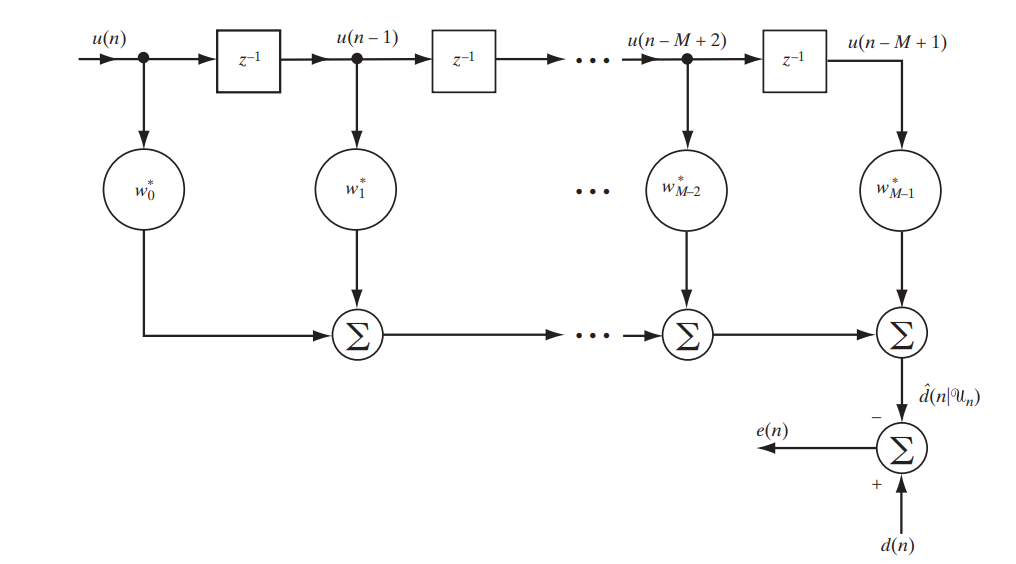
Fig.1. El esquema de filtro FIR para estudiar el filtro Wiener. [1. p.117]

Escribiremos en forma matricial lo que será exactamente a la salida de este stand:

$e (n) = d (n) - \ hat {d} (n | \ mathcal {U} _n) = d (n) - \ mathbf {w} ^ H \ mathbf {u} \ qquad (1)$

Descifrar la notación:

Es la diferencia (error) entre las señales dadas y recibidas
Es alguna señal predefinida
$\ mathbf {u}$ Es un vector de muestras o, en otras palabras, una señal en la entrada del filtro
$\ hat {d} (n | \ mathcal {U} _n)$ ¿Es la señal en la salida del filtro?
$\ mathbf {w} ^ H$ - esta es una conjugación hermitiana del vector de coeficiente de filtro - es en su selección óptima donde radica la adaptabilidad del filtro

Probablemente ya haya adivinado que buscaremos la menor diferencia entre la señal dada y la filtrada, es decir, el error más pequeño. Esto significa que nos enfrentamos a una tarea de optimización.

¿Qué vamos a optimizar?

Para optimizar, o más bien minimizar, no solo nos referiremos al error, el error cuadrático medio ( MSE - Error cuadrático medio ):

$MSE: J (\ mathbf {w}) = E \ {e (n) ^ 2 \} \ qquad (2)$

donde $J (\ mathbf {w})$ denota la función de costo del vector de coeficientes de filtro, y $E \ {* \}$ denota mat. esperando

El cuadrado en este caso es muy agradable, ya que significa que nos enfrentamos con el problema de la programación convexa (busqué en Google solo un análogo de la optimización convexa en inglés), que, a su vez, implica un extremo único (en nuestro caso, un mínimo).

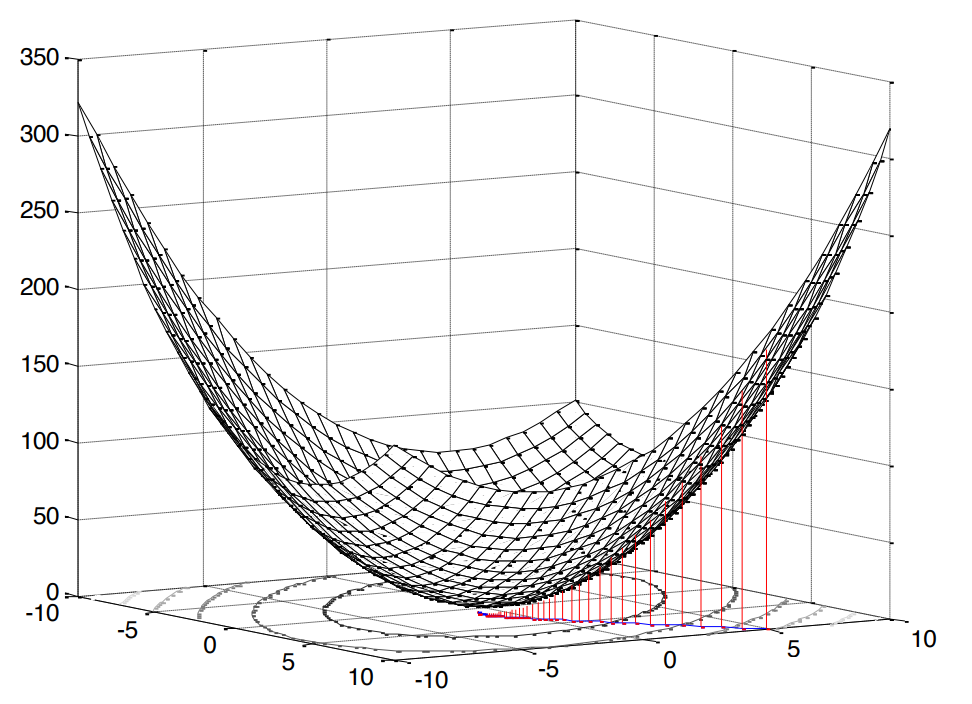
Fig.2. La superficie del error cuadrático medio .

Nuestra función de error tiene una forma canónica [1, p. 121]:

$J (\ mathbf {w}) = \ sigma ^ 2_d - \ mathbf {w} ^ H \ mathbf {p} - \ mathbf {p} ^ H \ mathbf {w} + \ mathbf {w} ^ H \ mathbf { R} \ mathbf {w} \ qquad (3)$

donde $\ sigma ^ 2_d$ Es la varianza de la señal esperada, $\ mathbf {p} = E \ {\ mathbf {u} (n) d ^ * (n) \}$ Es el vector de correlación cruzada entre el vector de entrada y la señal esperada, y $\ mathbf {R} = E \ {\ mathbf {u} (n) \ mathbf {u} ^ H (n) \}$ Es la matriz de autocorrelación de la señal de entrada.

La conclusión de esta fórmula está aquí (lo probé más claramente).

Como señalamos anteriormente, si estamos hablando de programación convexa, tendremos un extremo (mínimo). Entonces, para encontrar el valor mínimo de la función de costo (el mínimo error cuadrático medio), es suficiente encontrar la tangente de la pendiente de la tangente o, en otras palabras, la derivada parcial con respecto a nuestra variable estudiada:

$\ frac {\ delta J (\ mathbf {w})} {\ delta w ^ *} = - \ mathbf {p} + \ mathbf {R} \ mathbf {w} \ qquad (4)$

En el mejor de los casos ( $\ mathbf {w} = \ mathbf {w} _ {opt}$ ), el error debería ser, por supuesto, mínimo, lo que significa que equiparamos la derivada a cero:

$\ mathbf {R} \ mathbf {w} _ {opt} = \ mathbf {p} \ qquad (5)$

En realidad, aquí está, nuestra estufa, desde la cual bailaremos más: delante de nosotros hay un sistema de ecuaciones lineales .

¿Cómo vamos a decidir?

Cabe señalar de inmediato que ambas soluciones, que consideraremos a continuación, en este caso son teóricas y educativas, ya que $\ mathbf {R}$ y $\ mathbf {p}$ conocido de antemano (es decir, teníamos la supuesta capacidad de recopilar estadísticas suficientes para calcularlos). Sin embargo, el análisis de tales ejemplos simplificados aquí es lo mejor que puede pensar para comprender los enfoques básicos.

Solución analítica

Este problema puede resolverse, por así decirlo, en la frente, utilizando matrices inversas:

$\ mathbf {w} _ {opt} = \ mathbf {R} ^ {- 1} \ mathbf {p} \ qquad (6)$

Tal expresión se llama la ecuación de Wiener-Hopf; todavía es útil para nosotros como referencia.

Por supuesto, para ser completamente meticuloso, probablemente sería más correcto escribir este caso de manera general, es decir no con $^ {-}$ y con ( pseudoinvertir ):
$\ mathbf {R} ^ + = \ mathbf {R} ^ H (\ mathbf {R} \ mathbf {R} ^ H) ^ {- 1}$

Sin embargo, la matriz de autocorrelación no puede ser no cuadrada o singular, por lo tanto, con bastante razón, creemos que no hay contradicción.

A partir de esta ecuación, es analíticamente posible deducir cuál será el valor mínimo de la función de costo (es decir, en nuestro caso MMSE - error cuadrado mínimo mínimo):

$J_ {min} = J (\ mathbf {w} _ {opt}) = \ sigma ^ 2_d - \ mathbf {p} ^ H \ mathbf {R} ^ {- 1} \ mathbf {p} \ qquad (7)$

La derivación de la fórmula está aquí (también traté de hacerla más colorida).

Bueno, hay una solución.

Solución iterativa

Sin embargo, sí, es posible resolver un sistema de ecuaciones lineales sin invertir la matriz de autocorrelación de forma iterativa ( para guardar los cálculos ). Para este propósito, considere el método nativo y comprensible de descenso de gradiente ( método de descenso más pronunciado / gradiente ).

La esencia del algoritmo se puede reducir a lo siguiente:

Establecemos la variable deseada en algún valor predeterminado (por ejemplo, $\ mathbf {w} (0) = \ mathbf {0}$ )
Elige un paso $\ mu$ (cómo exactamente elegimos, hablaremos a continuación).
Y luego, por así decirlo, bajamos a lo largo de nuestra superficie original (en nuestro caso, esta es la superficie MSE) con un paso dado $\ mu$ y una cierta velocidad determinada por la magnitud del gradiente.

De ahí el nombre: gradiente - gradiente o más empinado - descenso gradual - descenso.

El gradiente en nuestro caso ya es conocido: de hecho, lo encontramos cuando diferenciamos la función de costo (la superficie es cóncava, compárela con [1, p. 220]). Escribimos cómo se verá la fórmula para la actualización iterativa de la variable deseada (coeficientes de filtro) [1, p. 220]:

$\ mathbf {w} (n + 1) = \ mathbf {w} (n) - \ mu [- \ mathbf {p} + \ mathbf {R} \ mathbf {w} (n)] \ qquad (8)$

donde Es el número de iteración.

Ahora hablemos de elegir un tamaño de paso.

Enumeramos las premisas obvias:

el paso no puede ser negativo o cero
el paso no debe ser demasiado grande, de lo contrario el algoritmo no convergerá (saltará de borde a borde, sin caer en el extremo)
el paso, por supuesto, puede ser muy pequeño, pero esto tampoco es del todo deseable: el algoritmo pasará más tiempo

Con respecto al filtro Wiener, las restricciones, por supuesto, ya se han encontrado hace mucho tiempo [1, p. 222-226]:

$0 <\ mu <\ frac {2} {\ lambda_ {max}} \ qquad (9)$

donde $\ lambda_ {max}$ Es el valor propio más grande de la matriz de autocorrelación. $\ mathbf {R}$ .

Por cierto, los valores propios y los vectores son un tema interesante aparte en el contexto del filtrado lineal. Incluso hay un filtro Eigen completo para este caso (ver Apéndice 1).

Pero esto, afortunadamente, no es todo. También hay una solución óptima y adaptativa:

$\ mu (n) = \ frac {\ mathbf {\ gamma} (n) ^ H \ mathbf {\ gamma} (n)} {\ mathbf {\ gamma} (n) ^ H \ mathbf {R} \ mathbf { \ gamma} (n)} \ qquad (10)$

donde $\ mathbf {\ gamma} (n) = \ mathbf {p} - \ mathbf {R} \ mathbf {w} (n)$ Es un gradiente negativo. Como se puede ver en la fórmula, el paso se relata en cada iteración, es decir, se adapta.

La conclusión de la fórmula está aquí (muchas matemáticas, mira solo a los mismos nerds notorios como yo).

De acuerdo, para la segunda decisión, también preparamos el escenario.

¿Pero es posible con ejemplos?

En aras de la claridad, realizaremos una pequeña simulación. Utilizaremos Python 3.6.4 .

Diré de inmediato que estos ejemplos son parte de una de las tareas asignadas, cada una de las cuales se ofrece a los estudiantes para su solución dentro de dos semanas. Reescribí la parte bajo Python (para popularizar el lenguaje entre los ingenieros de radio). Quizás encuentre otras opciones en la Web de otros antiguos alumnos.

import numpy as np import matplotlib.pyplot as plt from scipy.linalg import toeplitz def convmtx(h,n): return toeplitz(np.hstack([h, np.zeros(n-1)]),\ np.hstack([h[0], np.zeros(n-1)])) def MSE_calc(sigmaS, R, p, w): w = w.reshape(w.shape[0], 1) wH = np.conj(w).reshape(1, w.shape[0]) p = p.reshape(p.shape[0], 1) pH = np.conj(p).reshape(1, p.shape[0]) MSE = sigmaS - np.dot(wH, p) - np.dot(pH, w) + np.dot(np.dot(wH, R), w) return MSE[0, 0] def mu_opt_calc(gamma, R): gamma = gamma.reshape(gamma.shape[0], 1) gammaH = np.conj(gamma).reshape(1, gamma.shape[0]) mu_opt = np.dot(gammaH, gamma) / np.dot(np.dot(gammaH, R), gamma) return mu_opt[0, 0]

Utilizaremos nuestro filtro lineal para el problema de ecualización del canal , cuyo objetivo principal es nivelar los diversos efectos de este canal en la señal útil.

El código fuente se puede descargar en un archivo aquí o aquí (sí, tenía un pasatiempo, editar Wikipedia).

Modelo del sistema

Supongamos que hay un conjunto de antenas (ya lo examinamos en un artículo sobre MÚSICA ).

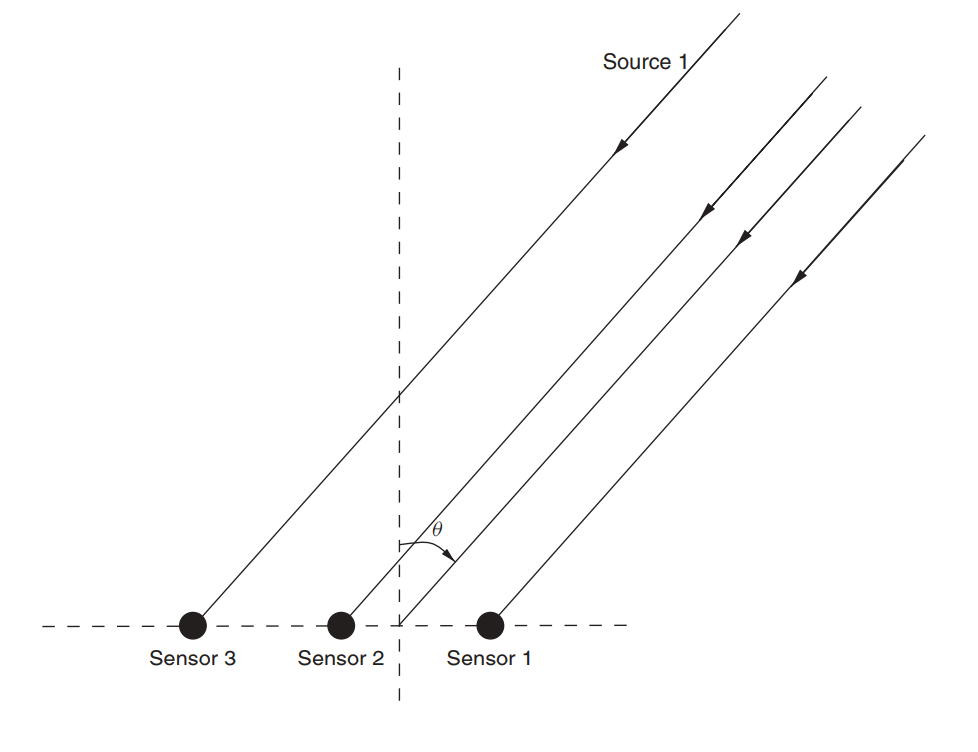
Fig. 3. Conjunto de antenas lineales no direccionales (ULAA - conjunto de antenas lineales uniforme) [2, p. 32]

Defina los parámetros iniciales de la red:

 M = 5 #    (number of sensors)

En este artículo, consideraremos algo así como un canal de banda ancha con desvanecimiento , una característica de la cual es la propagación por trayectos múltiples . Para tales casos, generalmente se aplica un enfoque en el que cada haz se modela utilizando un retraso de cierta magnitud (Fig. 4).

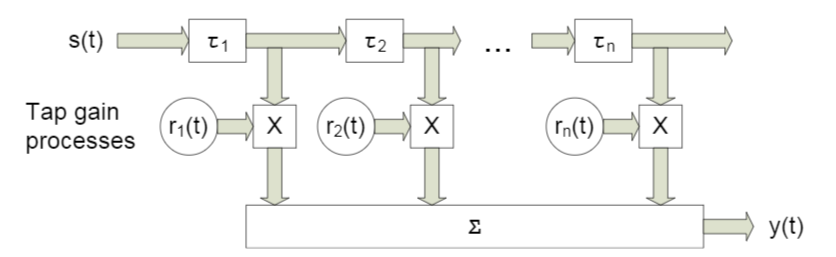
Fig. 4. El modelo del canal de banda ancha con n retrasos fijos. [3, p. 29] Como comprenderá, las designaciones específicas no juegan un papel, en lo que sigue utilizaremos algunas ligeramente diferentes.

El modelo de la señal recibida para un sensor se expresa de la siguiente manera:

$x (n) = \ sum_ {l = 0} ^ Lh (l) s (n-l) + \ nu (n)$

En este caso indica el número de referencia, h (l) Es la respuesta del canal a lo largo del l- ésimo haz, L es el número de registros de retardo, s es la señal transmitida (útil), $\ nu (n)$ - ruido aditivo.

Para varios sensores, la fórmula tomará la forma:

$\ mathbf {x} (n) = \ mathbf {H} \ mathbf {s} (n) + \ mathbf {\ nu} (n)$

donde $\ mathbf {x} (n)$ y $\ mathbf {\ nu} (n)$ - tener dimensión $M \ veces 1$ dimensión $\ mathbf {H}$ es igual a $M \ veces (M-L)$ y la dimensión $\ mathbf {s} (n)$ es igual $(M-L) \ veces 1$ .

Suponga que cada sensor también recibe una señal con cierto retraso, debido a la incidencia de la onda en ángulo. Matriz $\ mathbf {H}$ en nuestro caso, será una matriz convolucional para el vector de respuesta para cada rayo. Creo que el código será más claro:

 h = np.array([0.722-1j*0.779, -0.257-1j*0.722, -0.789-1j*1.862]) L = len(h)-1 # number of signal sources H = convmtx(h,ML) print(H.shape) print(H)

La conclusión será:

 >>> (5, 3) >>> array([[ 0.722-0.779j, 0. +0.j , 0. +0.j ], [-0.257-0.722j, 0.722-0.779j, 0. +0.j ], [-0.789-1.862j, -0.257-0.722j, 0.722-0.779j], [ 0. +0.j , -0.789-1.862j, -0.257-0.722j], [ 0. +0.j , 0. +0.j , -0.789-1.862j]])

A continuación, establecemos los datos iniciales para la señal y el ruido útiles:

 sigmaS = 1 #    (the signal's s(n) power) sigmaN = 0.01 #   (the noise's n(n) power)

Ahora pasamos a las correlaciones.

 Rxx = (sigmaS)*(np.dot(H,np.matrix(H).H))+(sigmaN)*np.identity(M) p = (sigmaS)*H[:,0] p = p.reshape((len(p), 1))

La derivación de las fórmulas aquí (también una hoja para los más desesperados).

Encontramos una solución para Wiener:

 # Solution of the Wiener-Hopf equation: wopt = np.dot(np.linalg.inv(Rxx), p) MSEopt = MSE_calc(sigmaS, Rxx, p, wopt)

Ahora pasemos al método de descenso de gradiente.

Encuentre el valor propio más grande para que el límite superior del paso pueda derivarse de él (vea la fórmula (9)):

 lamda_max = max(np.linalg.eigvals(Rxx))

Ahora establezcamos una serie de pasos que constituirán una cierta fracción del máximo:

 coeff = np.array([1, 0.9, 0.5, 0.2, 0.1]) mus = 2/lamda_max*coeff # different step sizes

Defina el número máximo de iteraciones:

 N_steps = 100

Ejecute el algoritmo:

 MSE = np.empty((len(mus), N_steps), dtype=complex) for mu_idx, mu in enumerate(mus): w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): w = w - mu*(np.dot(Rxx, w) - p) MSE[mu_idx, N_i] = MSE_calc(sigmaS, Rxx, p, w)

Ahora haremos lo mismo, pero para el paso adaptativo (fórmula (10)):

 MSEoptmu = np.empty((1, N_steps), dtype=complex) w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): gamma = p - np.dot(Rxx,w) mu_opt = mu_opt_calc(gamma, Rxx) w = w - mu_opt*(np.dot(Rxx,w) - p) MSEoptmu[:, N_i] = MSE_calc(sigmaS, Rxx, p, w)

Deberías obtener algo como esto:

Dibujo

 x = [i for i in range(1, N_steps+1)] plt.figure(figsize=(5, 4), dpi=300) for idx, item in enumerate(coeff): if item == 1: item = '' plt.loglog(x, np.abs(MSE[idx, :]),\ label='$\mu = '+str(item)+'\mu_{max}$') plt.loglog(x, np.abs(MSEoptmu[0, :]),\ label='$\mu = \mu_{opt}$') plt.loglog(x, np.abs(MSEopt*np.ones((len(x), 1), dtype=complex)),\ label = 'Wiener solution') plt.grid(True) plt.xlabel('Number of steps') plt.ylabel('Mean-Square Error') plt.title('Steepest descent') plt.legend(loc='best') plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()

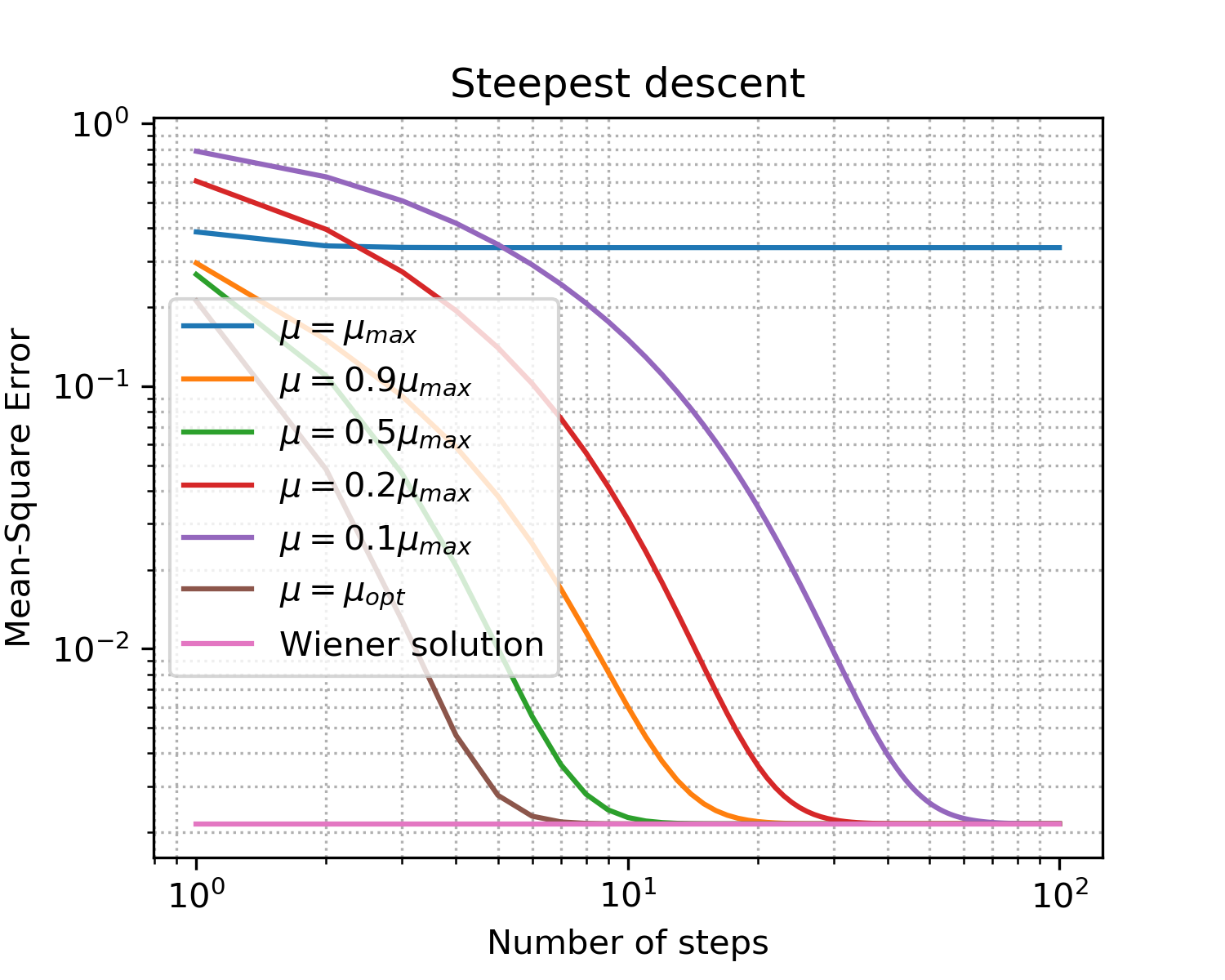
Fig. 5. Curvas de aprendizaje para pasos de diferentes tamaños.

Fijaciones por el simple hecho de hablar los puntos principales sobre el descenso de gradiente:

como se esperaba, el paso óptimo da la convergencia más rápida;
ya no significa mejor: habiendo excedido el límite superior, no hemos alcanzado la convergencia en absoluto.

Así que encontramos el vector óptimo de coeficientes de filtro que nivelará mejor los efectos del canal: hemos entrenado el ecualizador .

¿Hay algo más cercano a la realidad?

Por supuesto! Ya hemos dicho varias veces que recopilar estadísticas (es decir, calcular matrices de correlación y vectores) en sistemas en tiempo real está lejos de ser siempre un lujo asequible. Sin embargo, la humanidad se ha adaptado a estas dificultades: en lugar de un enfoque determinista en la práctica, se utilizan enfoques adaptativos . Se pueden dividir en dos grandes grupos [1, p. 246]:

probabilístico (estocástico) (por ejemplo, SG - Gradiente estocástico)
y basado en el método de mínimos cuadrados (por ejemplo, LMS : mínimos cuadrados mínimos o RLS : mínimos cuadrados recursivos)

El tema de los filtros adaptativos está bien representado en la comunidad de código abierto (ejemplos para python):

En el segundo ejemplo, me gusta especialmente la documentación. Sin embargo, ten cuidado! Cuando probé el paquete padasip , me encontré con dificultades para manejar números complejos (por defecto, float64 está implícito allí). Quizás surjan los mismos problemas al trabajar con otras implementaciones.

Los algoritmos, por supuesto, tienen sus propias ventajas y desventajas, cuya suma determina el alcance del algoritmo.

Echemos un vistazo rápido a los ejemplos: consideraremos los tres algoritmos SG , LMS y RLS que ya hemos mencionado (modelaremos en el lenguaje MATLAB, lo confieso, ya había espacios en blanco y reescribiremos todo para uniformizar Python por el bien de ... bueno ...).

Se puede encontrar una descripción de los algoritmos LMS y RLS , por ejemplo, en el muelle padasip .

La descripción de SG se puede encontrar aquí.

La principal diferencia del descenso de gradiente es un gradiente variable:

$\ mathbf {w} [n] = \ mathbf {w} [n-1] + \ mu \ left (\ mathbf {\ hat {p}} [n] - \ mathbf {\ hat {R}} _ {xx } [n] \ mathbf {w} [n-1] \ right)$

a las

$\ mathbf {\ hat {R}} _ {xx} [n] = \ frac {1} {n} \ left ((n-1) \ mathbf {\ hat {R}} _ {xx} [n-1 ] + \ mathbf {x} [n] \ mathbf {x} [n] ^ H \ right)$

$\ mathbf {\ hat {p}} [n] = \ frac {1} {n} \ left ((n-1) \ mathbf {\ hat {p}} [n-1] + \ mathbf {x} [ n] d [n] ^ * \ derecha)$

1) Un caso similar al considerado anteriormente.

Fuentes (MatLab / Octave).

Las fuentes se pueden descargar aquí .

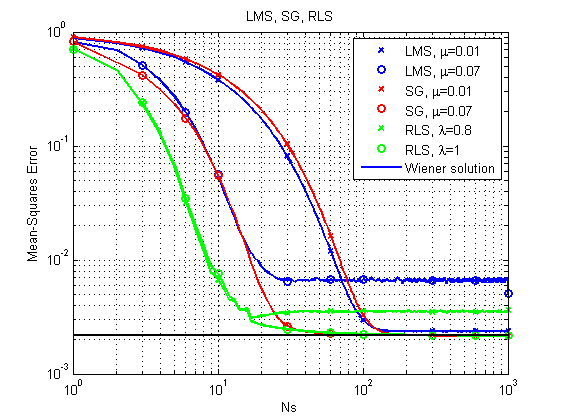
Fig. 6. Curvas de aprendizaje para LMS, RLS y SG.

Se puede notar de inmediato que, con su relativa simplicidad, el algoritmo LMS puede, en principio, no llegar a una solución óptima con un paso relativamente grande. RLS da el resultado más rápido, pero también puede fallar con un factor de olvido relativamente pequeño. Hasta ahora, SG está bien, pero veamos otro ejemplo.

2) El caso cuando el canal cambia en el tiempo.

Fuentes (MatLab / Octave).

Las fuentes se pueden descargar aquí .

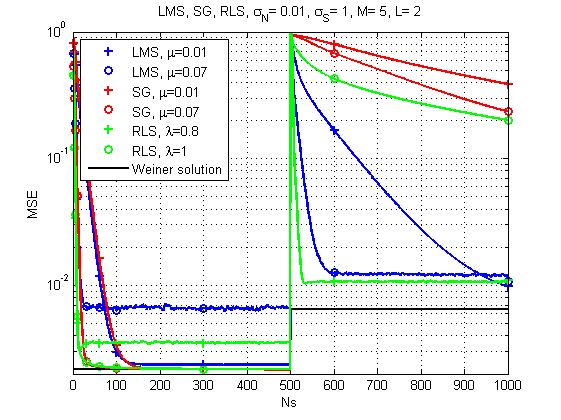
Fig. 7. Curvas de aprendizaje para LMS, RLS y SG (cambios de canal con el tiempo).

Y aquí la imagen ya es mucho más interesante: con un cambio brusco en la respuesta del canal, LMS ya parece ser la solución más confiable. ¿Quién lo hubiera pensado? Aunque RLS con el factor de olvido correcto también proporciona un resultado aceptable.

Algunas palabras sobre el rendimiento.

Sí, por supuesto, cada algoritmo tiene su propia complejidad computacional específica, pero según mis mediciones, mi vieja máquina puede hacer frente a un conjunto de aproximadamente 120 μs por iteración en el caso de LMS y SG y aproximadamente 250 μs por iteración en el caso de RLS. Es decir, la diferencia es, en general, comparable.

Y eso es todo por hoy. Gracias a todos los que miraron!

Literatura

Teoría de filtro adaptativo Haykin SS. - Pearson Education India, 2005.
Haykin, Simon y KJ Ray Liu. Manual sobre procesamiento de matriz y redes de sensores. Vol. 63. John Wiley & Sons, 2010. pp. 102-107
Arndt, D. (2015). Sobre el modelado de canales para la recepción satelital móvil terrestre (disertación doctoral).

Apéndice 1

Filtro Eigen

El objetivo principal de dicho filtro es maximizar la relación señal / ruido (SNR).

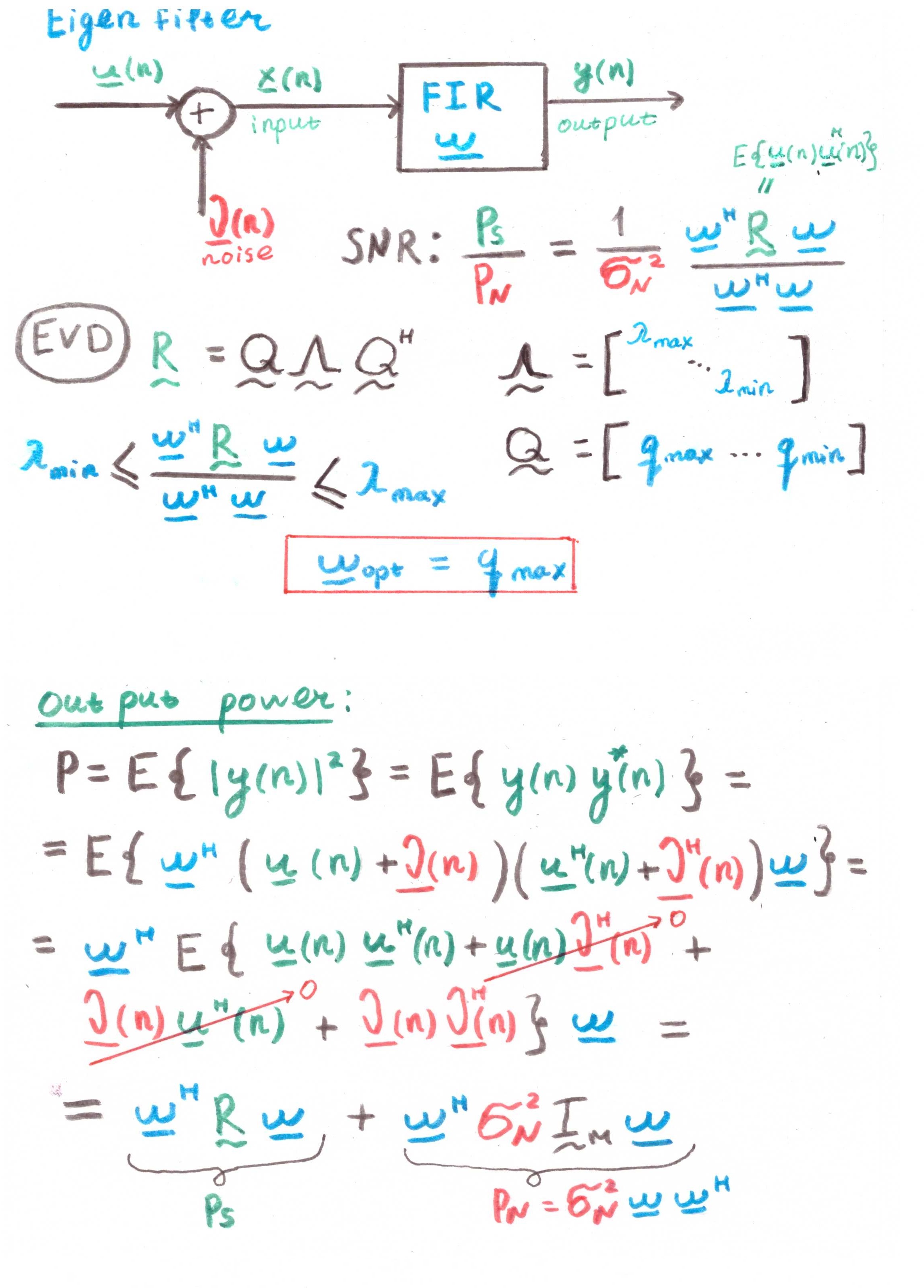
Pero a juzgar por la presencia de correlaciones en los cálculos, esto también es más una construcción teórica que una solución práctica.

Filtrado lineal óptimo: desde descenso de gradiente hasta filtros adaptativos