No es ningún secreto que uno de los pasatiempos favoritos para un desarrollador de software es entrevistar a empleadores. Todos hacemos esto de vez en cuando y por razones completamente diferentes. Y el más obvio de ellos, la búsqueda de empleo, creo que no es el más común. Asistir a una entrevista es una buena manera de mantenerse en forma, repetir conceptos básicos olvidados y aprender algo nuevo. Y si tiene éxito, también aumente la confianza en sí mismo. Nos aburrimos, nos fijamos en el estado de "abierto a ofertas" en algún tipo de red social "empresarial" como
"LinkedIn" , y el ejército de gerentes de recursos humanos ya está atacando nuestras bandejas de entrada para los mensajes entrantes.

En el proceso, mientras todo este caos está ocurriendo, nos enfrentamos a muchas preguntas que, como dicen al otro lado de la cortina colapsada implícitamente, están "sonando una campana", y sus detalles están ocultos detrás de la
niebla de la guerra . La mayoría de las veces se recuerdan en las pruebas mediante algoritmos y estructuras de datos (personalmente, no tenía esos datos en absoluto) y en realidad entrevistas.
Una de las preguntas más comunes en una entrevista para un programador de cualquier especialización son las listas. Por ejemplo, listas individualmente vinculadas. Y algoritmos básicos relacionados. Por ejemplo, un cambio de sentido. Y, por lo general, esto sucede de alguna manera como esta: "Bien, pero ¿cómo expandiría una lista individualmente vinculada?" Lo principal es sorprender al solicitante con esta pregunta.
En realidad, todo esto me llevó a escribir esta breve reseña para recordatorios y edificaciones constantes. Entonces, bromas aparte, ¡he aquí!
Lista vinculada individualmente
Una lista vinculada es una de las
estructuras de datos básicas. Cada elemento (o nodo) consiste en, de hecho, datos almacenados y enlaces a elementos vecinos. Una lista enlazada individualmente solo almacena un enlace al siguiente elemento en la estructura, y una lista
doblemente enlazada contiene el enlace al siguiente y al anterior. Dicha organización de datos les permite ubicarse en cualquier área de memoria (en contraste con, por ejemplo, una
matriz , cuyos elementos deben ubicarse en la memoria uno tras otro).
Hay mucho más que decir sobre las listas, por supuesto: pueden ser circulares (es decir, el último elemento almacena un enlace al primero) o no (es decir, no hay un enlace al último elemento). Las listas se pueden escribir, es decir contener datos del mismo tipo o no. Y así sucesivamente.
Mejor intente escribir algo de código. Por ejemplo, de alguna manera puedes imaginar un nodo de lista:
final class Node<T> { let payload: T var nextNode: Node? init(payload: T, nextNode: Node? = nil) { self.payload = payload self.nextNode = nextNode } }
"Genérico" es un tipo que es capaz de almacenar cargas útiles de cualquier tipo en el campo de
payload .
La lista en sí se identifica exhaustivamente por su primer nodo:
final class SinglyLinkedList<T> { var firstNode: Node<T>? init(firstNode: Node<T>? = nil) { self.firstNode = firstNode } }
El primer nodo se declara opcional, porque la lista puede estar vacía.
En teoría, por supuesto, en la clase debe implementar todos los métodos necesarios: insertar, eliminar, acceder a nodos, etc., pero lo haremos en otro momento. Al mismo tiempo, comprobaremos si usar struct (que Apple nos anima activamente con nuestro ejemplo) es una mejor opción, y quizás recordaremos el enfoque de "Copiar en escritura" .Lista de un solo enlace
La primera manera Ciclo
¡Es hora de comenzar a trabajar para lo que estamos aquí hoy! Y la forma más efectiva de lidiar con esto es de dos maneras. El primero es un bucle simple, desde el primero hasta el último nodo.
El ciclo funciona con tres variables, que antes del comienzo tienen asignado el valor del nodo anterior, actual y siguiente. (En este momento, el valor del nodo anterior está naturalmente vacío.) El ciclo comienza verificando que el siguiente nodo no esté vacío y, de ser así, se ejecuta el cuerpo del ciclo. No ocurre magia en el bucle: en el nodo actual, al campo que se refiere al siguiente elemento se le asigna un enlace al anterior (en la primera iteración, el valor del enlace, respectivamente, se restablece, lo que corresponde al estado del asunto en el último nodo). Bien y además, a las variables correspondientes al nodo anterior, actual y siguiente se les asignan nuevos valores. Después de salir del bucle, al nodo actual (es decir, el último iterable en general) se le asigna un nuevo valor de enlace al siguiente nodo, porque La salida del bucle se produce justo en el momento en que el último nodo de la lista se vuelve actual.
En palabras, por supuesto, todo esto suena extraño e incomprensible, así que mejor ver el código:
extension SinglyLinkedList { func reverse() { var previousNode: Node<T>? = nil var currentNode = firstNode var nextNode = firstNode?.nextNode while nextNode != nil { currentNode?.nextNode = previousNode previousNode = currentNode currentNode = nextNode nextNode = currentNode?.nextNode } currentNode?.nextNode = previousNode firstNode = currentNode } }
Para la verificación, utilizamos una lista de nodos cuyas cargas útiles son identificadores
enteros simples. Crea una lista de diez elementos:
let node = Node(payload: 0)
Todo parece estar bien, pero somos personas, no computadoras, y sería bueno para nosotros obtener una prueba visual de la exactitud de la lista creada y el algoritmo descrito anteriormente. Quizás una simple impresión será suficiente. Para que la salida sea legible, agregue la implementación del protocolo
CustomStringConvertible nodo con un identificador entero:
extension Node: CustomStringConvertible where T == Int { var description: String { let firstPart = """ Node \(Unmanaged.passUnretained(self).toOpaque()) has id \(payload) and """ if let nextNode = nextNode { return firstPart + " next node \(nextNode.payload)." } else { return firstPart + " no next node." } } }
... Y la lista correspondiente para mostrar todos los nodos en orden:
extension SinglyLinkedList: CustomStringConvertible where T == Int { var description: String { var description = """ List \(Unmanaged.passUnretained(self).toOpaque()) """ if firstNode != nil { description += " has nodes:\n" var node = firstNode while node != nil { description += (node!.description + "\n") node = node!.nextNode } return description } else { return description + " has no nodes." } } }
La representación de cadena de nuestros tipos contendrá una dirección en la memoria y un identificador entero. Utilizándolos, organizamos la impresión de la lista generada de diez nodos:
print(String(describing: list))
Expanda esta lista e imprímala nuevamente:
list.reverse() print(String(describing: list))
Puede notar que las direcciones en la memoria de la lista y los nodos no han cambiado, y los nodos de la lista se imprimen en el orden inverso. Las referencias al siguiente elemento del nodo ahora apuntan al anterior (es decir, por ejemplo, el siguiente elemento del nodo "5" ahora no es "6", sino "4"). ¡Y eso significa que lo hicimos!
El segundo camino. Recursividad
La segunda forma conocida de hacer el mismo giro en U se basa en la
recursividad . Para implementarlo, declararemos una función que toma el primer nodo de la lista y devuelve el primer nodo "nuevo" (que fue el último antes).
El parámetro y el valor de retorno son opcionales, porque dentro de esta función se llama una y otra vez en cada nodo posterior hasta que esté vacío (es decir, hasta que se llegue al final de la lista). En consecuencia, en el cuerpo de la función, es necesario verificar si el nodo en el que se llama la función está vacío y si este nodo tiene lo siguiente. De lo contrario, la función devuelve lo que se pasó al argumento.
En realidad, honestamente intenté describir el algoritmo completo en palabras, pero al final borré casi todo, porque el resultado sería imposible de entender. Dibujar diagramas de flujo y describir formalmente los pasos del algoritmo; también, en este caso, creo que no tiene sentido, porque será más conveniente para usted y para mí leer e intentar comprender el código
Swift :
extension SinglyLinkedList { func reverseRecursively() { func reverse(_ node: Node<T>?) -> Node<T>? { guard let head = node else { return node } if head.nextNode == nil { return head } let reversedHead = reverse(head.nextNode) head.nextNode?.nextNode = head head.nextNode = nil return reversedHead } firstNode = reverse(firstNode) } }
El algoritmo en sí está "envuelto" por un método del tipo de la lista real, para la conveniencia de llamar.
Parece más corto, pero, en mi opinión, más difícil de entender.
Llamamos a este método sobre el resultado de la propagación anterior e imprimimos un nuevo resultado:
list.reverseRecursively() print(String(describing: list))
En la salida se puede ver que todas las direcciones en la memoria no han cambiado nuevamente, y los nodos ahora siguen en el orden original (es decir, se "implementan" nuevamente). ¡Y eso significa que lo acertamos de nuevo!
Conclusiones
Si observa los métodos de inversión cuidadosamente (o realiza un experimento con el conteo de llamadas), notará que el bucle en el primer caso y la llamada al método interno (recursivo) en el segundo caso ocurren una vez menos que el número de nodos en la lista (en nuestro caso, nueve tiempos). También puede prestar atención a lo que sucede alrededor del ciclo en el primer caso, la misma secuencia de asignaciones, y a la primera llamada al método, no recursiva, en el segundo caso. Resulta que en ambos casos el "círculo" se repite exactamente diez veces para una lista de diez nodos. Por lo tanto, tenemos una
complejidad lineal para ambos algoritmos:
O (n) .
En términos generales, los dos algoritmos descritos se consideran los más efectivos para resolver este problema. En cuanto a la complejidad computacional, no es posible encontrar un algoritmo con un valor más bajo: de una forma u otra, debe "visitar" cada nodo para asignar un nuevo valor al almacenado dentro del enlace.
Otra característica que vale la pena mencionar es la "complejidad de memoria asignada". Ambos algoritmos propuestos crean un número fijo de nuevas variables (tres en el primer caso y una en el segundo). Esto significa que la cantidad de memoria asignada no depende de las características cuantitativas de los datos de entrada y se describe mediante una función constante: O (1).
Pero, de hecho, en el segundo caso esto no es así. El peligro de recurrencia es que se asigna memoria adicional para cada llamada recursiva en la
pila . En nuestro caso, la profundidad de recursión corresponde a la cantidad de datos de entrada.
Y finalmente, decidí experimentar un poco más: de una manera simple y primitiva medí el tiempo de ejecución absoluto de dos métodos para una cantidad diferente de datos de entrada. Así:
let startDate = Date().timeIntervalSince1970
Y esto es lo que obtuve (estos son los datos sin procesar del
Playground ):
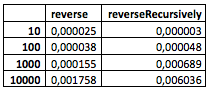
(Desafortunadamente, mi computadora no ha dominado los valores más grandes).
¿Qué se puede ver en la mesa? Nada especial todavía. Aunque ya es notable que el método recursivo se comporta un poco peor con un número relativamente pequeño de nodos, pero en algún lugar entre 100 y 1000 comienza a mostrarse mejor.
También probé la misma prueba simple dentro de un proyecto completo de
"Xcode" . Los resultados son los siguientes:

En primer lugar, vale la pena mencionar que los resultados se obtuvieron después de activar el modo de optimización "agresivo" dirigido a la velocidad de ejecución (
-Ofast ), que es en parte por qué los números son tan pequeños. También es interesante que en este caso el método recursivo se mostró un poco mejor, por el contrario, solo en tamaños muy pequeños de datos de entrada, y ya en una lista de 100 nodos, el método pierde. De 100,000, hizo que el programa terminara anormalmente.
Conclusión
Intenté cubrir un tema bastante clásico desde el punto de vista de mi lenguaje de programación favorito en este momento, y espero que tengas curiosidad por seguir el progreso tan bien como yo. Y estoy muy contento si también lograste aprender algo nuevo, entonces definitivamente perdí mi tiempo en este artículo (en lugar de sentarme y mirar
programas de televisión ).
Si alguien desea seguir mi actividad social, aquí hay un enlace a mi "Twitter" , donde, en primer lugar, hay enlaces a mis nuevas publicaciones y un poco más.