Conecte los autómatas celulares con el algoritmo genético y vea qué sucede.
El artículo contiene GIF (tráfico) e imágenes contrastantes. Los epilépticos pueden tener una crisis epiléptica.Reglas para autómatas celulares
El autómata celular más simple es un autómata celular unidimensional (también hay autómatas de dimensión cero; hablaremos de ellos a continuación). En un autómata celular unidimensional, tenemos una matriz unidimensional, cuyas celdas (celdas) pueden tomar uno de dos estados (1/0, verdadero / falso, blanco / negro, vivo / muerto). El siguiente estado de la celda en la matriz está determinado por el estado actual de la celda y el estado de dos celdas vecinas, de acuerdo con alguna regla.
El total existe
combinaciones de estados celulares y dos células vecinas:

A continuación, para cada una de las combinaciones, anotamos el estado de la celda para la próxima iteración (para el siguiente estado del autómata):
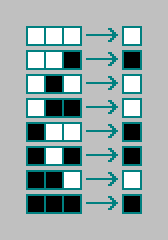
Tengo una regla para un autómata celular. Las reglas para autómatas celulares unidimensionales están codificadas con 8 bits ("código de tungsteno"). El total existe
autómatas celulares elementales:
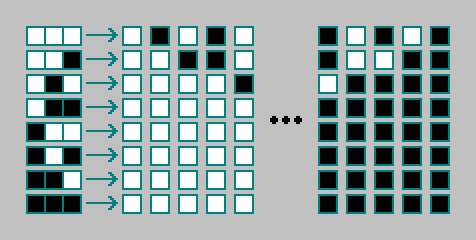
Se pueden clasificar 256 máquinas manualmente. No nos detendremos en ellos. Calculamos el número de reglas existentes para autómatas celulares bidimensionales.
Un autómata celular bidimensional utiliza una matriz bidimensional. Cada celda tiene 8 vecinos en las cercanías de Moore (también hay un vecindario de von Neumann en el que no se tienen en cuenta las celdas diagonales. No lo consideraremos en el artículo):

Por conveniencia, escribimos las celdas en una línea (usaremos el orden seleccionado más adelante en el artículo):
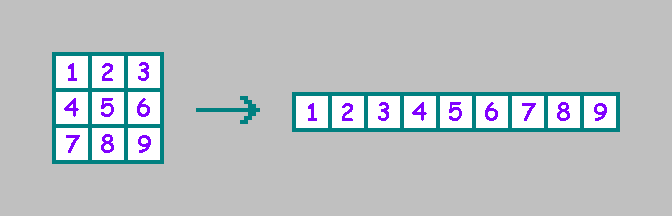
Para un autómata celular bidimensional existe
combinaciones de estados celulares y 8 células vecinas:

La regla para un autómata celular bidimensional está codificada con 512 bits. El total existe
autómatas celulares bidimensionales:
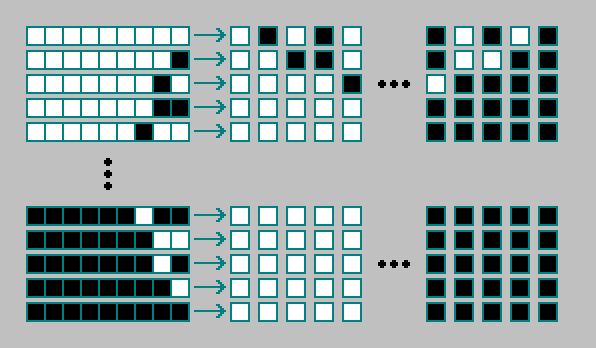
Numero:
más
átomos en el universo observable (
)
Manualmente, este número de máquinas no se puede resolver. Si miramos un autómata cada segundo, durante la existencia del Universo, habríamos logrado mirar todo
Máquinas automáticas.
La enumeración simple no funciona, pero con la ayuda de un algoritmo genético, podemos encontrar autómatas que mejor se ajusten a ciertos criterios predefinidos.
Lo programaremos en JavaScript. Todos los fragmentos de código están ocultos bajo spoilers para no confundir a los lectores que no están familiarizados con los lenguajes de programación.
Autómata celular bidimensional
Escribimos un autómata celular bidimensional con una regla aleatoria. Almacenaremos la regla en la matriz de reglas, cuya longitud de rulesize = 512:
Rellene la matriz de reglasvar rulesize=512; var rule=[]; for(var i=0;i<rulesize;i++) rule[i]=Math.round(Math.random());
A continuación, complete el estado inicial de la máquina con una casa aleatoria:
Rellenamos el estado inicial de la máquina. var sizex=89; var sizey=89; var size=2; var a=[]; for(var x=0;x<sizex;x++){ a[x]=[] for(var y=0;y<sizey;y++){ a[x][y]=Math.round(Math.random()); if(a[x][y]) context.fillRect(x*size, y*size, 1*size, 1*size); } }
(aquí y más adelante en el artículo, como el ancho y la altura de la máquina, se toma un número aleatorio, no muy grande ni muy pequeño número impar 89)La función que calcula el siguiente estado del autómata tiene el siguiente aspecto (para no ensuciarlo, eliminó la inicialización del lienzo):
Consideramos el siguiente estado del autómata function countpoints(){ var temp=[]; var xm, xp, ym, yp, q; for(var x=0;x<sizex;x++){ xm=x-1; if(xm==-1) xm=sizex-1; xp=x+1; if(xp==sizex) xp=0; temp[x]=[]; for(var y=0;y<sizey;y++){ ym=y-1; if(ym==-1) ym=sizey-1; yp=y+1; if(yp==sizey) yp=0; q=''+a[xm][ym]+a[x][ym]+a[xp][ym]+a[xm][y]+a[x][y]+a[xp][y]+a[xm][yp]+a[x][yp]+a[xp][yp]; q=parseInt(q, 2); temp[x][y]=rule[q]; if(temp[x][y]) context.fillRect(x*size, y*size, 1*size, 1*size); } } a=temp; }
Las variables xm y xp almacenan las coordenadas X del vecino a la izquierda y del vecino a la derecha (x menos yx más). Las variables ym e yp almacenan las coordenadas Y correspondientes.
Aquí:
El campo de la máquina se enrolla en un bagel. xm=x-1; if(xm==-1) xm=sizex-1; xp=x+1; if(xp==sizex) xp=0;
definimos condiciones de contorno periódicas (el campo del autómata es la superficie del toro).
Siguiente:
... más allá q=''+a[xm][ym]+a[x][ym]+a[xp][ym]+a[xm][y]+a[x][y]+a[xp][y]+a[xm][yp]+a[x][yp]+a[xp][yp]; q=parseInt(q, 2); temp[x][y]=rule[q];
en el orden anterior, escriba el contenido de las celdas en una cadena. Traducimos la cadena a un número decimal. Para esta combinación, encontramos en la matriz de reglas el estado que debe tomar la celda con las coordenadas x e y.
Opción optimizada q=a[xm][ym]; q=(q<<1)+a[x][ym]; q=(q<<1)+a[xp][ym]; q=(q<<1)+a[xm][y]; q=(q<<1)+a[x][y]; q=(q<<1)+a[xp][y]; q=(q<<1)+a[xm][yp]; q=(q<<1)+a[x][yp]; q=(q<<1)+a[xp][yp]; temp[x][y]=rule[q];
Después de todas las iteraciones, reemplace el estado anterior del autómata con uno nuevo:
reemplazar el estado anterior por uno nuevo Dibujamos un autómata usando la función setInterval:
setInterval timerId = setInterval(function() { countpoints(); }, 1);
Ejecutar en el navegadorRecomiendo iniciar la máquina con reglas aleatorias 10-20 veces antes de continuar leyendo el artículo.
Podemos ejecutar la máquina durante mucho tiempo con diferentes reglas aleatorias. La imagen que obtengamos no diferirá de la imagen en la pantalla del televisor en ausencia de una señal:

A continuación, pasemos a configurar nuestra "TV" utilizando el algoritmo genético.
Algoritmo genético
El tamaño de la población inicial es de 200 máquinas (individuos). Para las reglas, en lugar de una matriz unidimensional de regla, usaremos una matriz bidimensional de población. El primer índice (n) es el número del individuo en la población.
Crea una población var PopulationSize=200; var rulesize=512; var population=[]; var fitness=[]; for(var n=0;n<PopulationSize;n++){ population[n]=[]; fitness[n]=0; for(var i=0;i<rulesize;i++){ population[n][i]=Math.round(Math.random()); } }
La matriz de estado físico contiene los coeficientes de estado físico de cada individuo. Este conjunto se completa en el proceso de selección. Después de la selección, comenzamos el proceso evolutivo.
Proceso evolutivo
De nuestra población tomamos la mitad de los individuos más adaptados (según el coeficiente de aptitud física). La mitad restante está destruida. Luego, tomamos dos individuos sobrevivientes y los cruzamos.

Para cruzar, seleccione una posición aleatoria en los genotipos de dos antepasados. Antes de esta posición, tomamos genes de un antepasado, después de esta posición, de otro. Ponemos los genes seleccionados en el genotipo a un descendiente. Los genes restantes son para otro. Colocamos dos antepasados y dos descendientes en una nueva población. Al mismo tiempo, cada individuo participa en el cruce una vez.
Mutaciones Con una probabilidad del 5%, un gen seleccionado al azar muta (invierte) en cada individuo. Si aumenta la probabilidad de mutaciones, habrá mutantes más exitosos, pero al mismo tiempo, un mutante exitoso puede no tener tiempo para dejar descendencia exitosa antes de que mute nuevamente sin éxito. Volveremos a este tema más tarde.
Función evolutiva (); function evolute(){ var sizehalf=PopulationSize/2; var sizequarter=sizehalf/2; var arrayt=[]; for(var n=0; n<PopulationSize; n++) arrayt[n]=[population[n], fitness[n]]; arrayt.sort(sortf); arrayt.length=sizehalf; population=[]; fitness=[]; for(var i=0; i<sizequarter; i++){ var i0=i*4; var i1=i*4+1; var i2=i*4+2; var i3=i*4+3; var removed1=Math.floor(Math.random()*(arrayt.length)); var parent1f = arrayt.splice(removed1,1); var parent1=parent1f[0][0]; var removed2=Math.floor(Math.random()*(arrayt.length)); var parent2f = arrayt.splice(removed2,1); var parent2=parent2f[0][0]; var child1=[]; var child2=[]; var qen=Math.floor(Math.random()*rulesize); var temp0=parent1; var temp1=parent2; var temp2=temp0.splice(qen,rulesize); var temp3=temp1.splice(qen,rulesize); var parent1=temp0.concat(temp2); var parent2=temp1.concat(temp3); var child1=temp1.concat(temp2); var child2=temp0.concat(temp3); population[i0]=parent1; population[i1]=parent2; population[i2]=child1; population[i3]=child2; fitness[i0]=0; fitness[i1]=0; fitness[i2]=0; fitness[i3]=0; } var mutation=document.getElementById("mutatepercent").value*1; var m=100/mutation; var m2=0;
Selección natural
Antes de comenzar el proceso evolutivo, se debe hacer una selección. La selección puede ser tanto natural como artificial. La selección artificial se realiza manualmente, un poco más tarde. Para la selección natural, estableceremos algunos criterios y seleccionaremos las máquinas que mejor coincidan con los criterios dados.
¿Qué criterios se pueden determinar de antemano? Toma la más fácil. Nuestra "TV" parpadea demasiado. Guardamos dos estados del autómata celular: 99 y 100 iteraciones. Cuente el número de celdas que no han cambiado. El número resultante se usará como coeficiente de aptitud. Obviamente, un criterio no es suficiente para nosotros. Es fácil seleccionar manualmente el autómata que mejor cumpla con el criterio dado: el autómata [0,0,0, ..., 0] y el autómata [1,1,1, ..., 1]. En la primera iteración, estos dos autómatas se rellenan con ceros o unos y dejan de cambiar su estado. Definimos el segundo criterio: la diferencia entre el número de 0 y 1 (celdas) en la máquina no excede de 100 (el número se toma "de la excavadora").
array1: estado del autómata en la 99ª iteración. array2 - en la iteración número 100:
Consideramos function countfitness(array1, array2){ var sum=0; var a0=0; var a1=0; for(var x=0;x<sizex;x++){ for(var y=0;y<sizey;y++){ if(array1[x][y]==array2[x][y]) sum++; if(array1[x][y]==0){ a0++; }else{ a1++; } } } if(Math.abs(a0-a1)<100) return sum; return 0; }
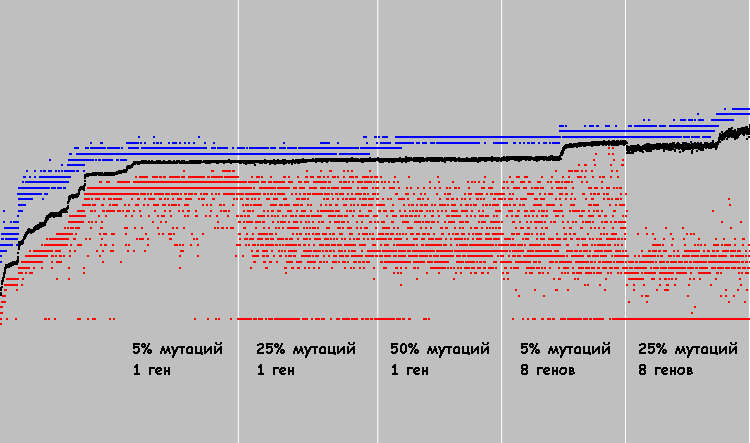
Empezamos La solución óptima se encontró en el 421º ciclo de evolución. En el gráfico puedes ver el progreso:
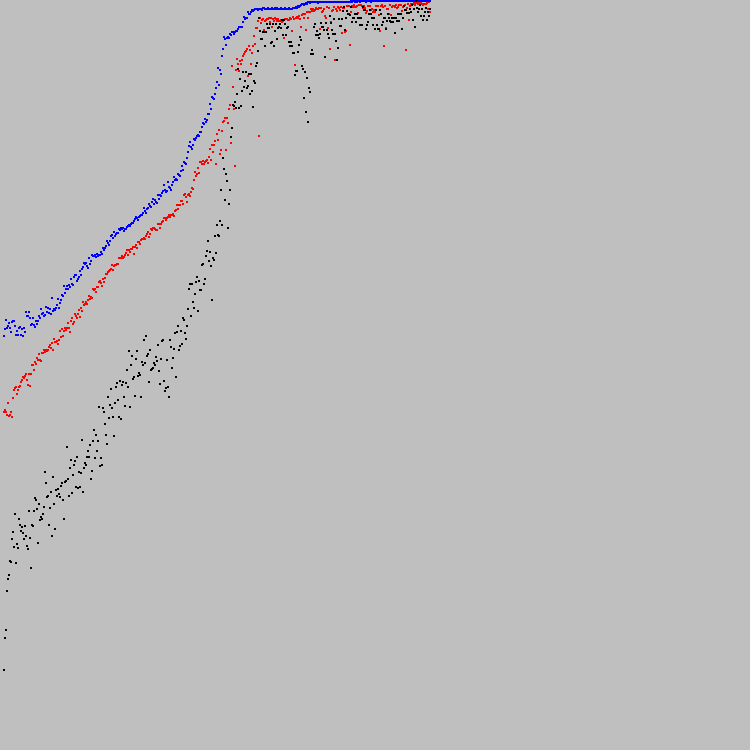
El gráfico se escala a lo largo del eje Y. El punto más bajo es 0, el punto más alto es 7921. Es obvio que 7921 es la solución óptima (todas las celdas de la máquina 89x89 cumplen el criterio especificado). Después de 100 iteraciones, ninguna celda cambia su estado.
Los puntos azules en el gráfico son el mejor individuo de la población. Los rojos son los peores (solo se tienen en cuenta las personas que cumplen con el segundo criterio). Puntos negros: el coeficiente promedio de aptitud para toda la población (teniendo en cuenta las personas que no cumplen con el segundo criterio). El segundo criterio (el equilibrio entre blanco y negro) es muy difícil. Algunos autómatas no cumplen el segundo criterio incluso después de 421 ciclos de evolución. Por lo tanto, los puntos negros están debajo del rojo.
El conjunto de genes de la población (individuos a lo largo del eje Y, genes a lo largo del eje X):

Veamos qué canal capturó nuestra "TV":

La solución encontrada no es la única óptima. Si volvemos a ejecutar la evolución (con genotipos iniciales aleatorios), encontraremos otras soluciones óptimas. Uno de ellos:

Cambiar los criterios de selección.
Consideraremos el número de celdas para las que aparece un patrón en las proximidades de Moore de orden 2. Tomemos el patrón más simple:
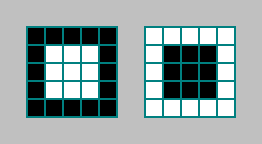
Este criterio es interesante porque verificamos 25 celdas, mientras que el autómata calcula el estado de la celda en función de los estados de 9 celdas.
El criterio es muy estricto. Si tomamos un autómata aleatorio, después de 100 iteraciones se ve así:

Ni una sola celda en un autómata cumple con el criterio dado. Por lo tanto, suavizamos un poco el criterio:
- Vamos a cometer un error en el patrón.
- No buscaremos el patrón en la última iteración, sino en las últimas 50 iteraciones.
El segundo criterio (el equilibrio entre blanco y negro) se elimina.
Empezamos Tabla:
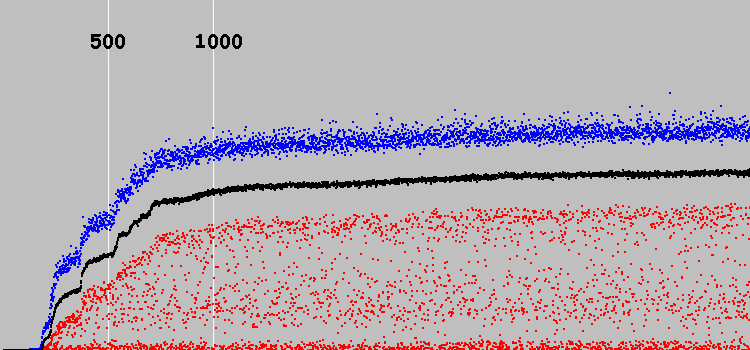
El eje y es arbitrario. (En la máquina anterior, la solución óptima es 7921. En esta máquina, alrededor de 30.)
Eje X - 3569 ciclos de evolución. Dos líneas verticales blancas marcan 500 y 1000 ciclos de evolución.
Puntos azules: el mejor individuo de la población, rojo: el peor, negro: la proporción promedio de toda la población.
La solución se encontró en los primeros 500 ciclos de evolución. Los próximos 500 ciclos, la solución mejora. Y luego el sistema prácticamente deja de evolucionar.
En las tres imágenes a continuación: 500 ciclos, 1000 ciclos y 3569 ciclos de evolución:



Fondo genético (3569):

En dinámica:

En la siguiente imagen, puede ver cómo se forma el oscilador (planeador) en esta máquina:

Podemos iniciar la máquina con el estado inicial en el que se llena una celda. Luego, arregle todas las combinaciones de celdas que se encuentran en las siguientes iteraciones del autómata. Una matriz de genes (genotipo de un autómata) es una matriz de todas las combinaciones posibles. Habiendo aislado solo las combinaciones que ocurren, podemos notar fácilmente todos los genes que están involucrados en la formación del oscilador. Las barras grises son genes que no participan en la formación del oscilador:

Las mutaciones en estos genes no se arraigan debido al hecho de que interrumpen la formación del patrón.
En nuestra máquina, un patrón (cuadrado) se forma solo alrededor de una celda negra. Intentemos iniciar el proceso evolutivo junto con el segundo criterio: la diferencia entre el número de células blancas y negras no excede de 400.
Comenzamos 3569 ciclos de evolución. Tabla:
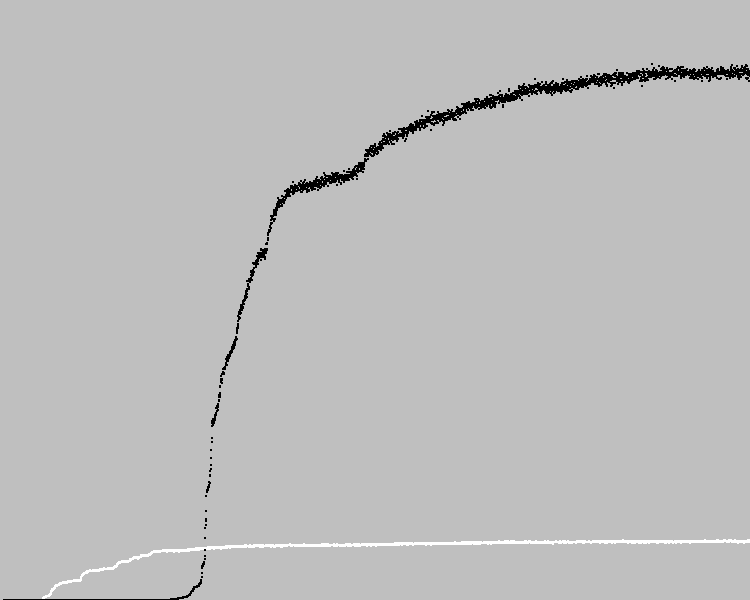
Los puntos negros en el gráfico son el coeficiente de aptitud física promedio en una población. Puntos blancos: el coeficiente promedio de aptitud de la máquina anterior. Encontró una solución con un error en el patrón.
Fondo genético:

100 primeras iteraciones:

Última (100) iteración:

Un poco no el resultado que esperábamos. Hay cuadrados negros, blancos - no. Apriete el segundo criterio: la diferencia entre el número de celdas blancas y negras no excede de 100.
Comenzamos 14865 ciclos de evolución.
El gráfico compara los coeficientes de aptitud promedio de las poblaciones. Los puntos azules son nuestra ametralladora. El blanco y el negro son máquinas anteriores.

Un autómata evoluciona tan vigorosamente que puede parecer que no evoluciona en absoluto. El segundo gráfico se escala a lo largo del eje Y. Dos líneas blancas: 500 y 1000 ciclos.
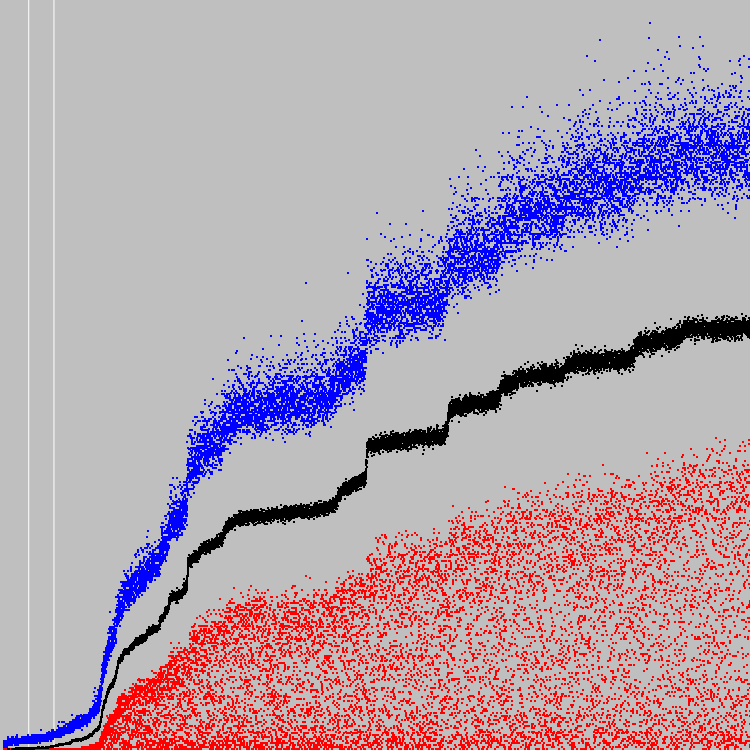
En el mejor individuo, en promedio, 6 celdas corresponden a un criterio dado.
Veamos una máquina aleatoria de una población.
50 iteraciones:

Última (50) iteración:

No se encontraron resultados aceptables. El segundo criterio complica la búsqueda, por lo que lo rechazaremos (no lo usaremos más adelante en el artículo). Dejemos este patrón y busquemos algunos otros patrones.
Patrón:

Empezamos 3000 ciclos de evolución. Tabla:
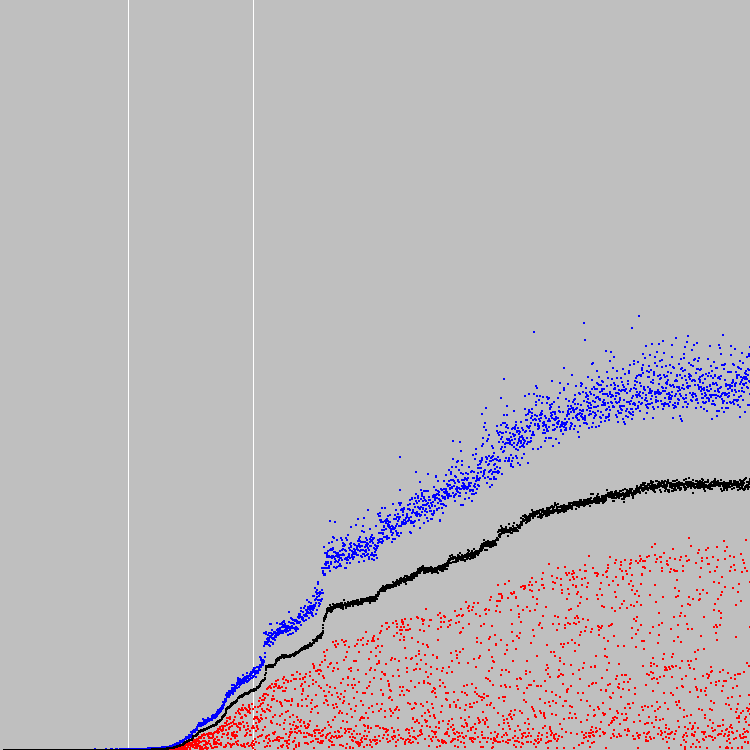
Fondo genético:

En dinámica (100 iteraciones):

Última (100) iteración:

Patrón:

En máquinas anteriores, permitimos cometer un error en el patrón. Esta vez, busquemos el patrón exacto.
Comenzamos 4549 ciclos de evolución. Tabla:
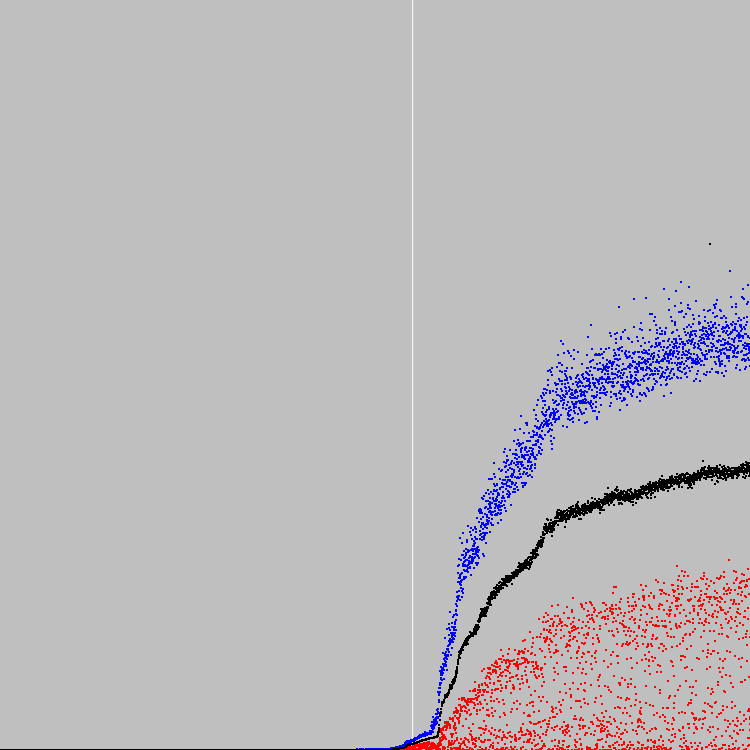
Línea vertical blanca: 2500 ciclos de evolución. En este punto (un poco antes), la aptitud de la población comenzó a crecer rápidamente. Salvó a la población para buscar una solución provisional. La solución intermedia resultó ser mucho más interesante que la solución en el 4549º ciclo de evolución.
Solución encontrada en el ciclo 4549 de evolución:

Hay 100 iteraciones en Gif. Después de un cierto número de iteraciones (aproximadamente 500-2000), el estado del autómata se ordena casi por completo (la altura y el ancho del autómata se eligen especialmente por números impares para que el autómata no se pueda ordenar por completo):

Un autómata con tamaños pares de lados, después de un cierto número de iteraciones, toma un estado completamente ordenado. Automático 90x90, aproximadamente 1200 iteraciones:

Solución intermedia (encontrada en el ciclo 2500 de evolución):

Este autómata también puede procesar un cierto estado caótico inicial en un cierto estado ordenado finito (el estado ordenado final es el desplazamiento del patrón a lo largo del eje X hacia la izquierda + varias celdas osciladoras).
La máquina 16x16 se ha solucionado en aproximadamente 100 iteraciones:

32x32 - aproximadamente 1000 iteraciones:

64x64 - aproximadamente 6000 iteraciones:

90x90 - aproximadamente 370000 iteraciones:

11x11 (dimensiones impares del campo del autómata) - aproximadamente 178700 iteraciones:

El rifle de asalto 13x13 no se racionalizó en un período de tiempo aceptable.
En la imagen a continuación, la máquina en el campo 256x256 en la iteración número 100,000:

Recomiendo mirar este autómata en dinámica en un campo grande: es muy interesante observar el proceso de autoorganización del caos en este autómata:
ejecutar en un navegadorFondo genético de la población intermedia:

Reiniciar el proceso evolutivo le permite encontrar otras soluciones. Uno de ellos:


Otro patrón:
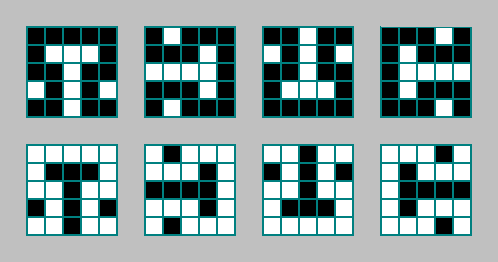
Al buscar un patrón, volvamos a cometer un error (sin errores, el sistema con el patrón seleccionado no evoluciona).
Empezamos 5788 ciclos de evolución. Tabla:
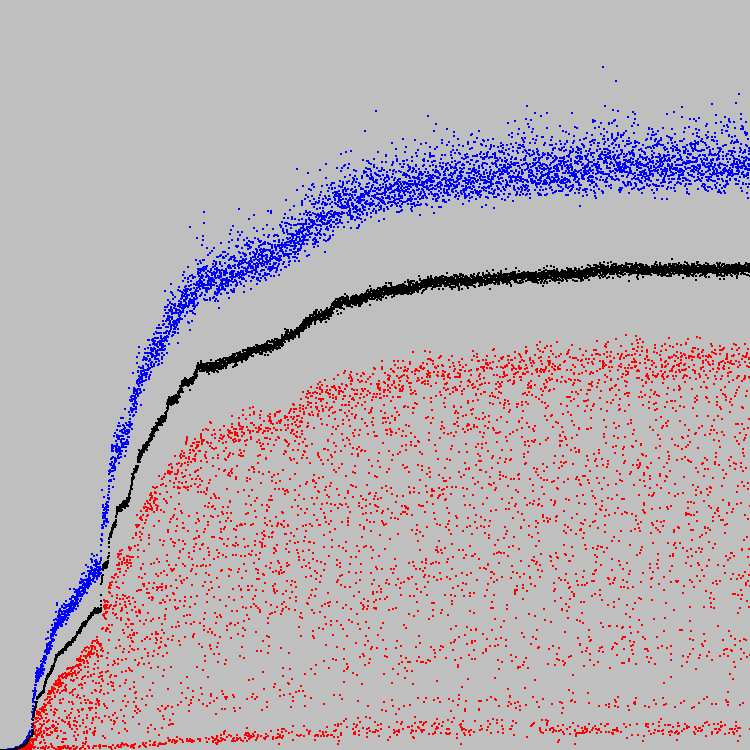
La escala es arbitraria.
Fondo genético:

En dinámica:

El estado ordenado del autómata (desplazamiento del patrón hacia arriba a lo largo del eje Y + varias celdas del oscilador):

Es mucho más interesante observar no la máquina en sí, sino los mutantes que aparecen en esta población:
En Gif, la máquina es 256x256. 200 iteraciones Las iteraciones restantes se pueden
ver en el navegador .
Uno podría terminar con la selección natural y pasar a la artificial, pero quiero mostrar cuánto
Un gran número. Entre este número de autómatas, podemos encontrar un autómata que dibuja cualquier patrón dado (con cierta precisión para patrones más complejos).
El siguiente patrón:

En experimentos anteriores, contamos la suma de celdas alrededor de las cuales se forma un patrón (si con un error, agregue 1 a la suma, si sin errores, agregue 2). La cantidad resultante se usó como un factor de aptitud para el algoritmo genético.
Para un patrón más complejo, este método no funciona. Un autómata en el que un número menor de celdas coincide más estrechamente con un criterio dado (el número de celdas que coinciden con el patrón en la vecindad de la celda) perderá cada vez más a un autómata en el que un mayor número de celdas coincide con menos precisión con un criterio dado. Como en el ejemplo con los cuadrados de arriba:

Para el patrón deseado, en la iteración número 100 de cada autómata en la población, rodeado por cada celda, consideraremos el número de celdas que coinciden con el patrón. Tomaremos solo el mejor resultado para cada máquina. El número de celdas que coincida con el patrón se utilizará como factor de aptitud. El patrón consta de 7x17 = 119 celdas. Este número se considerará la solución óptima. 6000 ciclos de evolución nos permitieron encontrar un autómata que dibuja un patrón con 5 errores (114 celdas coinciden con el patrón).
Gráfico en una escala arbitraria:
Un aumento en el porcentaje de mutaciones no perjudicó la aptitud de la población.
Hay muchos mutantes en el acervo genético de la población:

Un autómata aleatorio de una población en dinámica:

La mejor máquina en la iteración número 100:

Patrones buscados y encontrados:

Después de jugar con los criterios de selección, el tamaño del campo del autómata y el porcentaje de mutaciones, resultó mejorar la población y encontrar un autómata que solo comete 3 errores en el patrón.
Fondo genético:

Máquina en la iteración número 100:

Patrones buscados y encontrados:

2 erroresEn el proceso de escribir el artículo, el sistema continuó evolucionando. Para una búsqueda más precisa, el tamaño del campo de la máquina se ha incrementado a 513x513. Se encontró un autómata que solo comete dos errores en el patrón:

En cuatro gráficos, puede ver cómo evoluciona el sistema con diferentes probabilidades de mutación (1 gen muta):
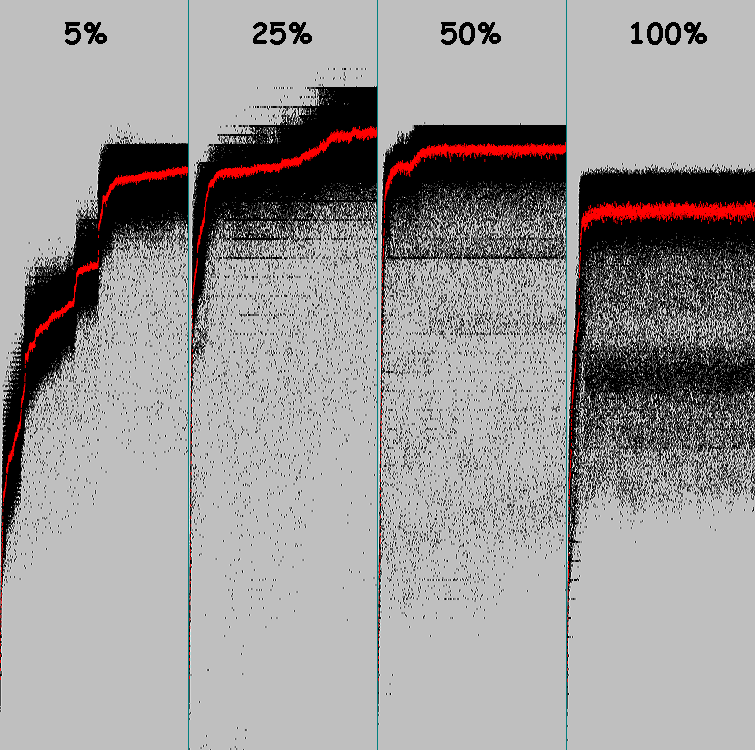
Los puntos rojos son el coeficiente de condición física promedio en una población. Los puntos negros son el coeficiente de aptitud de cada individuo. 3000 ciclos de evolución para cada sistema.
Grupos genéticos de poblaciones (en el mismo orden):




Autómatas en la iteración número 100:




Hagamos otro experimento. El patrón es el mismo. Los genotipos iniciales están llenos de genes aleatorios. La probabilidad de mutaciones es del 5%. De 1 a 8 genes mutan (se toma un número aleatorio de genes mutantes para cada individuo). 100 ciclos de evolución.

El gráfico es un mapa de calor. El tamaño en puntos en el gráfico es de 5 píxeles. El origen es la esquina superior izquierda.
En el eje Y (de 0 a 100) - ciclos de evolución. En el eje X (de 0 a 119), el número de celdas que coinciden con el patrón (para cada individuo de la población tomamos el mejor resultado). El brillo del punto es el número de individuos con el resultado especificado (coordenada X).
Ejecute el algoritmo genético 4 veces con los mismos parámetros (100 ciclos, 5% de mutaciones, hasta 8 genes mutan). En el gráfico, los 5 comienzan:

Los siguientes 5 comienzos: 25% de mutaciones, hasta 8 genes mutan:

La muestra es pequeña, pero podemos sacar conclusiones sobre la efectividad de aumentar el porcentaje de mutaciones.
A continuación, mostraré la ineficiencia del método de cruce utilizado en el artículo.
Método utilizado previamente:

En lugar de dividir el genotipo en dos partes, los descendientes heredarán genes ancestrales aleatorios:
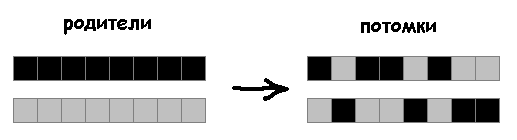
5% de mutaciones:

25%:

A continuación usaremos este método de cruces.
Sobre esto con acabado de selección natural. Si alguien tiene ideas interesantes sobre los criterios para la selección natural, por favor dígalo en los comentarios.
Para la selección artificial usaremos
autómatas celulares de segundo orden .
Autómata celular de segundo orden
Considere un autómata celular de dimensión cero de primer orden (todos los autómatas celulares que consideramos anteriormente son de primer orden). Un autómata celular de dimensión cero consiste en una célula. Una celda puede estar en uno de dos estados. El siguiente estado de la celda (t) está determinado por el estado actual de la celda (t-1). En total, hay 4 autómatas celulares de dimensión cero (entre ellos un oscilador):
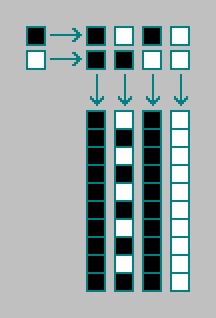
En un autómata celular de segundo orden, el siguiente estado de la celda (t) está determinado por el estado actual (t-1) y el estado anterior de la celda (t-2). En total, hay 4 combinaciones de dos estados celulares.
- el número de autómatas celulares de dimensión cero del segundo orden:

Tales autómatas celulares exhiben osciladores más complejos.
autómatas celulares de tercer orden:

los autómatas celulares de cuarto orden no se pueden mostrar en una imagen.
Búsqueda de autómata celular -o orden con un período de oscilación igual a - La tarea no es trivial y extremadamente interesante. Este tema merece un artículo separado.En autómatas celulares unidimensionales de segunda dimensión, el siguiente estado de una celda está determinado por el estado actual de tres celdas y el estado anterior de una celda:
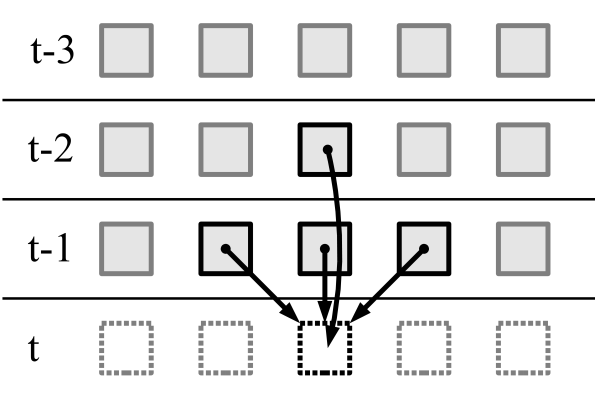
Hay
autómatas celulares unidimensionales de segundo orden.
Código:
var rule=[]; for(var i=0;i<16;i++) rule[i]=Math.round(Math.random()); var a=[]; var b=[]; var temp; for(var x=0;x<sizex;x++){ a[x]=0; b[x]=0; } b[63]=1; var xm, xp, q; for(var y=2;y<sizey;y++){ temp=[]; for(var x=0;x<sizex;x++){ xm=x-1; if(xm<0) xm=sizex+xm; xp=x+1; if(xp>=sizex) xp=xp-sizex; q=b[xm]; q=(q<<1)+b[x]; q=(q<<1)+b[xp]; q=(q<<1)+a[x]; temp[x]=rule[q]; if(temp[x]) context.fillRect(x*size, y*size, size, size); } a=b; b=temp; }
 0101101110011110:
0101101110011110: 0110000110010010:
0110000110010010: 0110011010010110:
0110011010010110: 1110011010010110:
1110011010010110: 0110111010000101:
0110111010000101: 1111101001110110:
1111101001110110: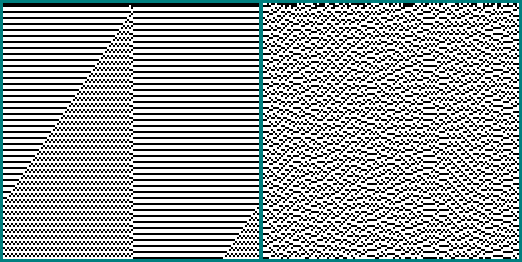 1001010001100000:
1001010001100000: La misma máquina
La misma máquina 256x256 : 512x512 Aquí
256x256 : 512x512 Aquí se pueden ver otras máquinas:Máquina celular unidimensional de segundo orden.Autómata celular unidimensional de tercer orden.Los autómatas celulares unidimensionales de segundo orden se pueden encontrar en el libro de Wolfram A New Kind of Science.
se pueden ver otras máquinas:Máquina celular unidimensional de segundo orden.Autómata celular unidimensional de tercer orden.Los autómatas celulares unidimensionales de segundo orden se pueden encontrar en el libro de Wolfram A New Kind of Science.Selección artificial
Al igual que un autómata celular unidimensional del segundo orden, en un autómata celular bidimensional del segundo orden usaremos una celda adicional del estado anterior (t-2) del autómata.Para mayor comodidad, colocamos esta celda al comienzo de la línea binaria: la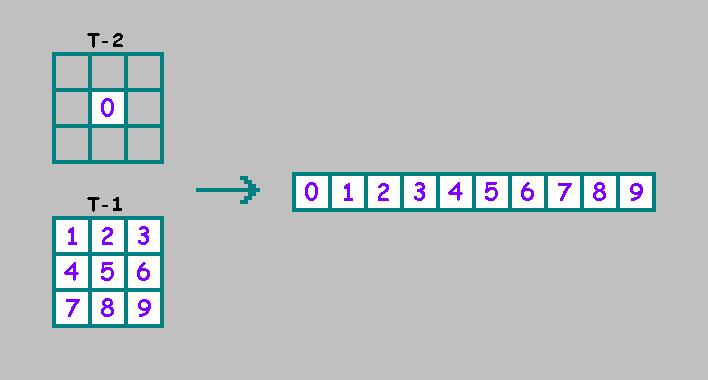 conveniencia radica en el hecho de que cuando la primera y la segunda mitad del genotipo coinciden, el autómata puede considerarse como un autómata de primer orden:
conveniencia radica en el hecho de que cuando la primera y la segunda mitad del genotipo coinciden, el autómata puede considerarse como un autómata de primer orden: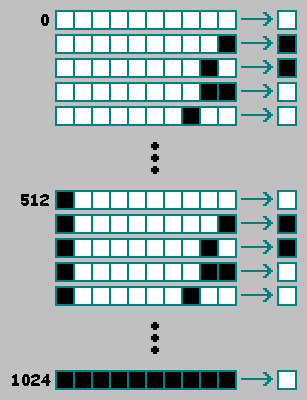 al agregar una celda, aumentamos el número de autómatas existentes en veces.- el número de autómatas bidimensionales existentes de segundo orden. Para la selección natural, determinamos algunos criterios y comparamos los autómatas según este criterio. En el proceso de selección artificial, seleccionamos las máquinas manualmente, utilizando un principio poco claro: "esta máquina es interesante, pero eso no es muy". Este principio no le permite elegir la mejor máquina entre las máquinas aleatorias:hay varias formas de resolver este problema. Propongo considerar cuatro formas.
al agregar una celda, aumentamos el número de autómatas existentes en veces.- el número de autómatas bidimensionales existentes de segundo orden. Para la selección natural, determinamos algunos criterios y comparamos los autómatas según este criterio. En el proceso de selección artificial, seleccionamos las máquinas manualmente, utilizando un principio poco claro: "esta máquina es interesante, pero eso no es muy". Este principio no le permite elegir la mejor máquina entre las máquinas aleatorias:hay varias formas de resolver este problema. Propongo considerar cuatro formas.





1. En el estado inicial de la máquina, se llena una celda
Una forma es observar el desarrollo de un autómata celular, en el estado inicial del cual se llena una célula.Llenamos la población inicial con máquinas aleatorias. Varias máquinas de la población inicial (30 iteraciones para cada una):

 Un pequeño número de autómatas que exhiben un comportamiento menos caótico están presentes en la población. Los seleccionaremos para cruzar:
Un pequeño número de autómatas que exhiben un comportamiento menos caótico están presentes en la población. Los seleccionaremos para cruzar:




 20 máquinas aleatorias de la población inicial (estado de las máquinas en la 30ª iteración):
20 máquinas aleatorias de la población inicial (estado de las máquinas en la 30ª iteración): Después de tres ciclos de evolución:
Después de tres ciclos de evolución: Después de ocho ciclos de evolución:
Después de ocho ciclos de evolución: Ocho ciclos de evolución fueron suficientes para llenar a toda la población con una máquina con cierto rasgo (una máquina que dibuja triángulos) .
Ocho ciclos de evolución fueron suficientes para llenar a toda la población con una máquina con cierto rasgo (una máquina que dibuja triángulos) .2. El genotipo está parcialmente lleno
Si se viola la proporción de unidades y ceros en el genotipo, se viola la proporción de unidades y ceros en el fenotipo.En el genotipo (regla) del autómata, se registran las siguientes condiciones celulares para todas las combinaciones posibles de la célula y las células vecinas. Si hay más ceros (o unos) en el genotipo, entonces los ceros (o unos) se acumulan en los siguientes estados del autómata. Es interesante observar la correlación entre la razón de unos y ceros en el genotipo y la razón de unos y ceros en el fenotipo.Construye un cuadro.Crea una población de 200 máquinas. Rellenamos los genotipos con ceros (1024 genes en el genotipo de un autómata bidimensional de segundo orden). Siguiente genes están llenos de unidades. Para la primera población , para la población 513 .
A lo largo del eje es el número de población. A lo largo del ejeMarque y (con puntos blancos) la proporción de unos y ceros en el conjunto de genes de la población. Tenemos una hipérbola:para cada autómata (con un tamaño de campo de 89x89), consideramos 100 iteraciones. En la iteración número 100, contamos el número de unos y ceros en el estado (fenotipo) de cada autómata. Marcamos en el gráfico la razón de unidades y ceros (el número total de todas las unidades se divide por el número total de todos los ceros). Obtuvimos una curva: enlugar de la razón total de unos y ceros en todos los fenotipos, puede ver la razón de unos y ceros en cada fenotipo:en el lado izquierdo del gráfico hay puntos con la mayor desviación del valor promedio. Se puede suponer que estos son autómatas en cuyos genotipos el gen cero es igual a la unidad. Supuesto - verificado. Establecemos el gen cero siempre igual a cero. Dibujamos un nuevo cuadro: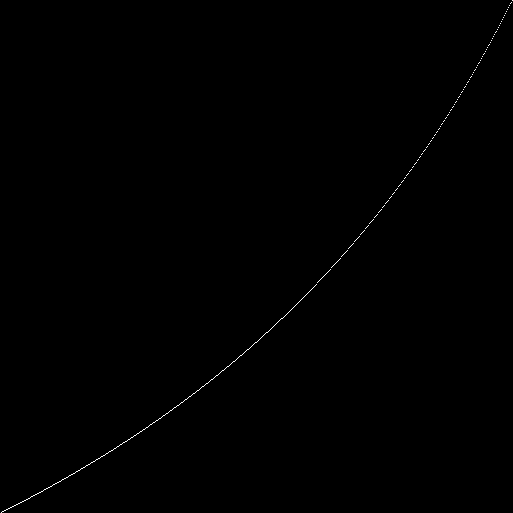
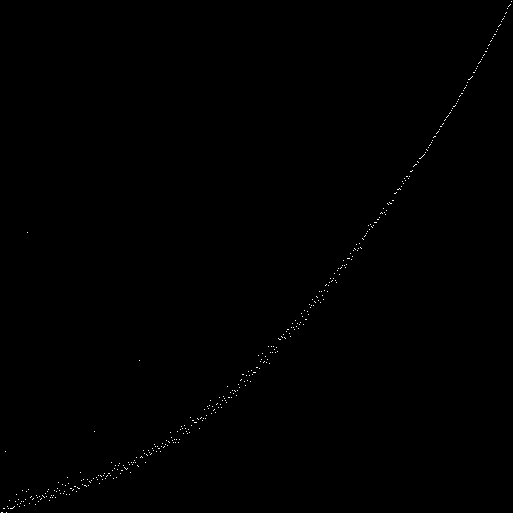

 Compare con máquinas en las que el gen cero siempre es igual a uno:
Compare con máquinas en las que el gen cero siempre es igual a uno: en las máquinas de segundo orden, hay otro gen "cero": el 512. Veamos cómo este gen afecta el fenotipo.Los genes 0 y 512 siempre son cero: el
en las máquinas de segundo orden, hay otro gen "cero": el 512. Veamos cómo este gen afecta el fenotipo.Los genes 0 y 512 siempre son cero: el gen 0 siempre es cero. El gen 512 siempre es igual a uno:
gen 0 siempre es cero. El gen 512 siempre es igual a uno: para no volver a burlarse de nuestros estimados epilépticos, los genes 0 y 512 se llenarán con ceros en la población inicial del algoritmo genético.Veamos las máquinas de las que nos deshacemos al poner ceros en los genes 0 y 512.Los primeros 8 estados de un autómata en el que solo se llena el gen 0 (el gen cero es uno, el resto son ceros): Un
para no volver a burlarse de nuestros estimados epilépticos, los genes 0 y 512 se llenarán con ceros en la población inicial del algoritmo genético.Veamos las máquinas de las que nos deshacemos al poner ceros en los genes 0 y 512.Los primeros 8 estados de un autómata en el que solo se llena el gen 0 (el gen cero es uno, el resto son ceros): Un autómata en el que solo
autómata en el que solo se llena el gen 512: Un autómata en el que solo se llenan los genes 0 y 512:
se llena el gen 512: Un autómata en el que solo se llenan los genes 0 y 512: Señalemos un lugar en el gráfico donde la población comienza a dividirse en grupos:
Señalemos un lugar en el gráfico donde la población comienza a dividirse en grupos: en este lugar, los genotipos están llenos en un 25%.Compara dos poblaciones.Primera población 30 máquinas aleatorias en la iteración número 1000. Los genotipos están llenos al 50% (512 unidades y 512 ceros):
en este lugar, los genotipos están llenos en un 25%.Compara dos poblaciones.Primera población 30 máquinas aleatorias en la iteración número 1000. Los genotipos están llenos al 50% (512 unidades y 512 ceros): la segunda población. 30 máquinas aleatorias en la iteración número 1000. Los genotipos están llenos en un 25% (256 unidades y 768 ceros):
la segunda población. 30 máquinas aleatorias en la iteración número 1000. Los genotipos están llenos en un 25% (256 unidades y 768 ceros): la segunda población es adecuada para la selección artificial. Podemos destacar fácilmente algunos de los signos en tales máquinas. Por ejemplo: "más oscuro", "menos caótico" (autómatas en los que se agrupan los glóbulos blancos), etc.Seleccionamos "más oscuro". La probabilidad de mutaciones es del 10%, hasta 4 genes mutan. Después de la primera selección:
la segunda población es adecuada para la selección artificial. Podemos destacar fácilmente algunos de los signos en tales máquinas. Por ejemplo: "más oscuro", "menos caótico" (autómatas en los que se agrupan los glóbulos blancos), etc.Seleccionamos "más oscuro". La probabilidad de mutaciones es del 10%, hasta 4 genes mutan. Después de la primera selección: Después de la segunda selección:
Después de la segunda selección: Un autómata interesante apareció en la población.256x256, estado de la máquina en la iteración número 1000: la
Un autómata interesante apareció en la población.256x256, estado de la máquina en la iteración número 1000: la máquina llena gradualmente a la población.Después de la octava selección:
máquina llena gradualmente a la población.Después de la octava selección: apareció otra máquina interesante.256x256, estado del autómata en la iteración número 1000:
apareció otra máquina interesante.256x256, estado del autómata en la iteración número 1000: Población después de trece selecciones:
Población después de trece selecciones: Varios autómatas de esta población. 256x256, iteración número 1000 para todos. Debajo de la imagen hay un enlace, haciendo clic en el cual puede ver la máquina en la dinámica:
Varios autómatas de esta población. 256x256, iteración número 1000 para todos. Debajo de la imagen hay un enlace, haciendo clic en el cual puede ver la máquina en la dinámica: Ver en dinámica.
Ver en dinámica. Ver en dinámica.
Ver en dinámica. Ver en dinámica.
Ver en dinámica. Ver en dinámica.
Ver en dinámica. Ver en dinámica.
Ver en dinámica. Ver en dinámica.
Ver en dinámica. Ver en dinámica.
Ver en dinámica. Ver en dinámica.
Ver en dinámica. Ver en dinámica.
Ver en dinámica. Ver en dinámica.
Ver en dinámica.3. Máquina automática Conway y similares.
El autómata celular bidimensional más famoso de primer orden es el autómata Conway Game "Life" .Las reglas para el autómata Conway están escritas de la siguiente manera:si hay 3 células vivas alrededor de una célula muerta, la célula cobra vida (de lo contrario, permanece muerta).Si hay 2 o 3 células vivas alrededor de una célula viva, la célula permanece viva (de lo contrario, muere).Una célula muerta es 0, una célula viva es 1.Alrededor de una célula puede haber de 0 a 8 células vivas. Según 9 opciones en torno a los vivos y alrededor de la celda muerta. Escribimos todas las opciones en la matriz r:matriz r r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ];
La primera mitad de la matriz es para una célula muerta, la segunda para una célula viva.Podemos describir la regla del autómata Conway para todas las combinaciones posibles (512) de una celda y 8 celdas vecinas:Pintar la regla r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ]; var rule=[]; var q1, q2; for(var i=0;i<512;i++){ var ii=i.toString(2); for(var j=ii.length;j<9;j++) ii='0'+ii; q1=1*ii[4]; q2=1*ii[0]+1*ii[1]+1*ii[2]+1*ii[3]+1*ii[5]+1*ii[6]+1*ii[7]+1*ii[8]; if(q1==0) rule[i]=r[q2]; else rule[i]=r[q2+9]; }
Opción optimizada r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ]; var rule=[]; for(var i=0;i<512;i++){ var q=((i>>4)&1)*8; for(var j=0;j<9;j++){ q+=(i>>j)&1; } rule[i]=r[q]; }
Para un autómata de segundo orden, copie la segunda mitad de la matriz de reglas de la primera:Copia for(var i=0;i<512;i++){ if(rule[i]==0) rule[i+512]=0; else rule[i+512]=1; }
Iniciamos la máquina con la regla especificada. Vemos los planeadores y osciladores característicos. Varias iteraciones de este autómata: la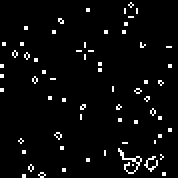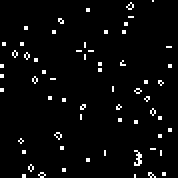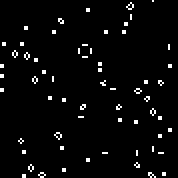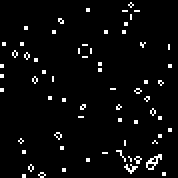 matriz r consta de 18 celdas. Hay autómatas similares al autómata de Conway (que puede escribirse con las mismas reglas: el número de células vivas rodeadas por los muertos, en el que la célula cobra vida y el número de células vivas en el entorno en el que muere la célula).Puede verlosaquí(de manera predeterminada, se inicia el autómata Conway, el botón "Cambiar regla" llena la matriz r al azar).Múltiples máquinas aleatorias (código binario - matriz r):110010011001111111100001100110111110011111000100101110010000110000110010001111010011100111000111001000000110000101100010100001000001111101011111000001100110111111
matriz r consta de 18 celdas. Hay autómatas similares al autómata de Conway (que puede escribirse con las mismas reglas: el número de células vivas rodeadas por los muertos, en el que la célula cobra vida y el número de células vivas en el entorno en el que muere la célula).Puede verlosaquí(de manera predeterminada, se inicia el autómata Conway, el botón "Cambiar regla" llena la matriz r al azar).Múltiples máquinas aleatorias (código binario - matriz r):110010011001111111100001100110111110011111000100101110010000110000110010001111010011100111000111001000000110000101100010100001000001111101011111000001100110111111





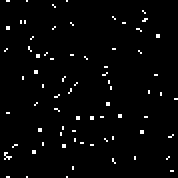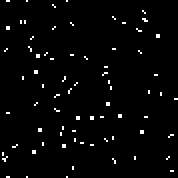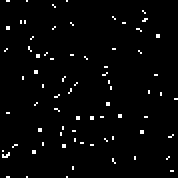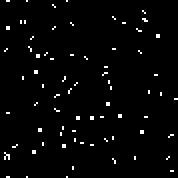

 Para un algoritmo genético, como genotipo, puede usar, como una matriz r ( combinaciones), y la matriz de reglas ( combinaciones de primer orden para el autómata celular y - para un autómata celular de segundo orden).es un número relativamente pequeño. Este número le permite seleccionar la regla para la máquina manualmente, sin usar un algoritmo genético (de hecho, lo que hizo Conway). Si llena la matriz de reglas con máquinas aleatorias de este tipo y utiliza esta matriz como un genotipo, entonces el experimento puede considerarse infructuoso, hasta cierto punto (lo suficiente como para no mostrar los resultados de este experimento en el artículo). En las reglas de autómatas celulares de este tipo, hay simetría. Por ejemplo, para las siguientes combinaciones de celdas:
Para un algoritmo genético, como genotipo, puede usar, como una matriz r ( combinaciones), y la matriz de reglas ( combinaciones de primer orden para el autómata celular y - para un autómata celular de segundo orden).es un número relativamente pequeño. Este número le permite seleccionar la regla para la máquina manualmente, sin usar un algoritmo genético (de hecho, lo que hizo Conway). Si llena la matriz de reglas con máquinas aleatorias de este tipo y utiliza esta matriz como un genotipo, entonces el experimento puede considerarse infructuoso, hasta cierto punto (lo suficiente como para no mostrar los resultados de este experimento en el artículo). En las reglas de autómatas celulares de este tipo, hay simetría. Por ejemplo, para las siguientes combinaciones de celdas: El estado de la celda en la siguiente iteración es el mismo. Después del primer cruce, se rompe la simetría en las reglas de los individuos descendientes. Los individuos ancestrales acumulan mutaciones que también destruyen la simetría. La violación de la simetría en el genotipo causa una violación de la simetría en el fenotipo.Se puede ver la manifestación de esta simetría en el fenotipo si una célula se llena en el estado inicial del autómata.Hagamos un experimento. Para mantener la simetría, utilizaremos la matriz r como genotipo. 5% de mutaciones, 1 gen muta. En el estado inicial, se llena una celda.30 máquinas aleatorias de la población inicial. El estado de los autómatas en la trigésima iteración:
El estado de la celda en la siguiente iteración es el mismo. Después del primer cruce, se rompe la simetría en las reglas de los individuos descendientes. Los individuos ancestrales acumulan mutaciones que también destruyen la simetría. La violación de la simetría en el genotipo causa una violación de la simetría en el fenotipo.Se puede ver la manifestación de esta simetría en el fenotipo si una célula se llena en el estado inicial del autómata.Hagamos un experimento. Para mantener la simetría, utilizaremos la matriz r como genotipo. 5% de mutaciones, 1 gen muta. En el estado inicial, se llena una celda.30 máquinas aleatorias de la población inicial. El estado de los autómatas en la trigésima iteración: intentemos aislar los autómatas que se desarrollan (crecen) más lentamente a partir de una célula.
intentemos aislar los autómatas que se desarrollan (crecen) más lentamente a partir de una célula.



 Después de la primera selección, se deshicieron de los autómatas que no se desarrollan:
Después de la primera selección, se deshicieron de los autómatas que no se desarrollan: en la nueva población hay varios autómatas (que no se desarrollan), estos son descendientes y mutantes sin éxito.A continuación, seleccionaremos principalmente máquinas con un fondo blanco (celdas en las que la máquina no se ha desarrollado).
en la nueva población hay varios autómatas (que no se desarrollan), estos son descendientes y mutantes sin éxito.A continuación, seleccionaremos principalmente máquinas con un fondo blanco (celdas en las que la máquina no se ha desarrollado).Las máquinas expendedoras negras parpadean.( — ) — . ( ) ( ). . — () . ( — , — ). 30- , — . ( 30- ) — ( ).
Población después de la segunda selección: 3 selecciones:
3 selecciones: 5 selecciones:
5 selecciones: 8 selecciones:
8 selecciones: 13 selecciones:
13 selecciones: Las mismas máquinas en la 60ª iteración:
Las mismas máquinas en la 60ª iteración: 21 selecciones. El estado de los autómatas en la 30ª iteración: El
21 selecciones. El estado de los autómatas en la 30ª iteración: El estado de los autómatas en la 60ª iteración:
estado de los autómatas en la 60ª iteración: 34 selecciones. Estado de autómatas en la 30ª iteración:
34 selecciones. Estado de autómatas en la 30ª iteración: Estado de autómatas en la 60ª iteración:
Estado de autómatas en la 60ª iteración: Además, el sistema no evoluciona. Tres autómatas de esta población (100 iteracionescada uno ): [1,0,1,1,1,0,0,1,0,0,1,1,0,1,0,1,1,1]
Además, el sistema no evoluciona. Tres autómatas de esta población (100 iteracionescada uno ): [1,0,1,1,1,0,0,1,0,0,1,1,0,1,0,1,1,1] [1 , 0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1]
[1 , 0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1] [1,0,0,1,1,0,0, 1,1,0,1,0,1,1,0,1,1,1]
[1,0,0,1,1,0,0, 1,1,0,1,0,1,1,0,1,1,1] En comparación, una máquina aleatoria:[1,0,0,1,1,1,0,1,1,1,0, 0,1,1,0,0,0,1]
En comparación, una máquina aleatoria:[1,0,0,1,1,1,0,1,1,1,0, 0,1,1,0,0,0,1]
4. Autómata de Conway y similares (2)
En las máquinas con las reglas del tipo Conway, contamos el número de unidades de células en las cercanías de Moore. Este vecindario se puede dividir en 4 pares y contar el número de células vivas en estos pares: por lo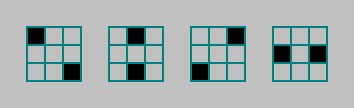 tanto, aumentamos el número de autómatas, pero mantenemos la simetría en el fenotipo.Cada par puede tener de 0 a 2 células vivas. Par 4. Número de combinaciones
tanto, aumentamos el número de autómatas, pero mantenemos la simetría en el fenotipo.Cada par puede tener de 0 a 2 células vivas. Par 4. Número de combinaciones .
De acuerdo con la combinación 81 en torno a los vivos y alrededor de la célula muerta. El total existe máquinas automáticas de este tipo. Numero:
Es completamente astronómico y se ajustará a un algoritmo genético.El tamaño del genotipo de cada individuo es de 162 genes:Llenar la población con máquinas aleatorias. var rulesize=162; for(var n=0;n<PopulationSize;n++){ population[n]=[]; fitness[n]=0; for(var i=0;i<rulesize;i++){ population[n][i]=Math.round(Math.random()); } }
A continuación, pintamos esta regla para todas las combinaciones posibles de una celda y ocho celdas vecinas:Función fillrule (); function fillrule(){ var r; for(var n=0;n<PopulationSize;n++){ rule[n]=[]; r=population[n]; var q1, q2, q3, q4, q5; var q; for(var i=0;i<512;i++){ var ii=i.toString(2); for(var j=ii.length;j<9;j++) ii='0'+ii; q1=1*ii[4]; q2=1*ii[0]+1*ii[8]; q3=1*ii[1]+1*ii[7]; q4=1*ii[2]+1*ii[6]; q5=1*ii[3]+1*ii[5]; q=parseInt(''+q2+q3+q4+q5,3); if(q1==0) rule[n][i]=r[q]; else rule[n][i]=r[q+81]; } } }
Usaremos la matriz de reglas cuando calculemos el siguiente estado del autómata. Llamamos a la función fillrule () después de cargar la página y después de llamar a la función evolute ().La población inicial parece caótica. 30 máquinas aleatorias, iteración número 1000: este caos varía ligeramente en dinámica y las máquinas son bastante adecuadas para la selección, pero hagámoslo más fácil: elegiremos las "más oscuras".Población después de cinco selecciones: a
este caos varía ligeramente en dinámica y las máquinas son bastante adecuadas para la selección, pero hagámoslo más fácil: elegiremos las "más oscuras".Población después de cinco selecciones: a continuación, puede buscar máquinas con los osciladores más complejos. Todo el proceso de diseño no tiene sentido. A continuación se presentan algunos de los autómatas más interesantes que se encuentran utilizando el algoritmo genético.256x256, iteración 10000 para todos. Debajo de la imagen hay un enlace, haciendo clic en el cual puede ver la máquina en la dinámica:
continuación, puede buscar máquinas con los osciladores más complejos. Todo el proceso de diseño no tiene sentido. A continuación se presentan algunos de los autómatas más interesantes que se encuentran utilizando el algoritmo genético.256x256, iteración 10000 para todos. Debajo de la imagen hay un enlace, haciendo clic en el cual puede ver la máquina en la dinámica: Ver en dinámica.
Ver en dinámica. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.?
Y puedes jugar por aquí:autómatas celulares bidimensionales de segundo orden.Interfaz: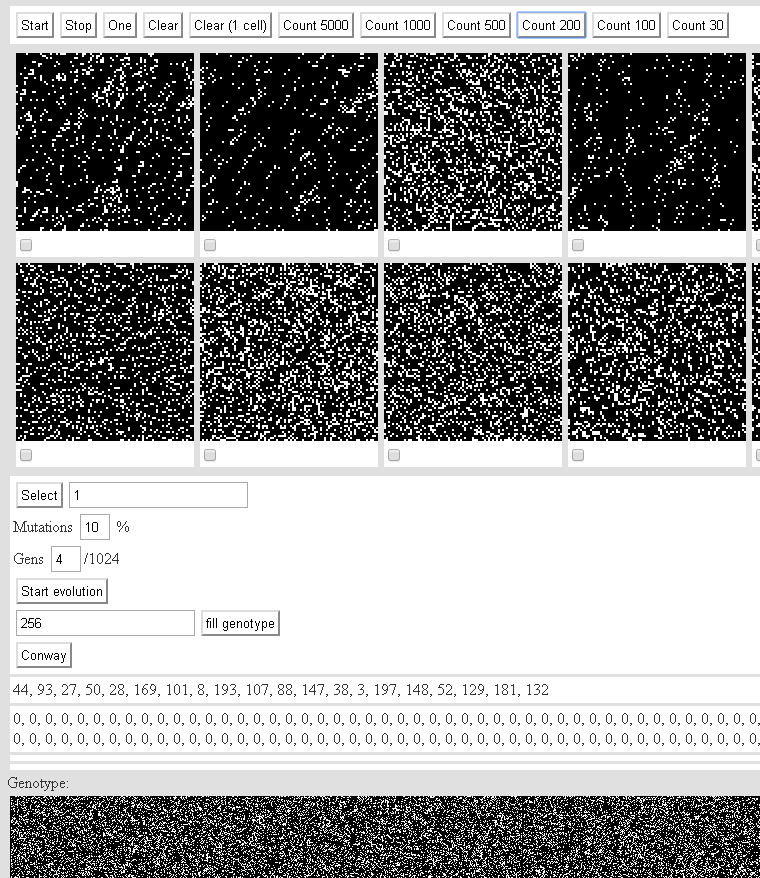 el botón Inicio inicia las máquinas.Stop - se detiene.Uno es una iteración.Borrar: detiene la máquina y llena el estado inicial de forma aleatoria.Borrar (1 celda): detiene la máquina y llena una celda en el estado inicial.Los botones restantes en esta línea cuentan el número especificado de iteraciones para cada autómata.Renderizar un autómata en lienzo consume todo el rendimiento. Si necesita calcular rápidamente 200 iteraciones, haga clic en Count 200. No hacemos clic en el botón Count 5000, el navegador puede colgarlo.Menos de 20 máquinas aleatorias (tamaño de la población - 200 máquinas). Debajo de las máquinas expendedoras casillas de verificación. Marcamos lo más interesante. Presione Seleccionar: el estado físico de la máquina aumentará en el número indicado a la derecha.Mutaciones: la probabilidad de mutaciones.Gens es el número de genes mutantes.Iniciar evolución: lanza el mecanismo de cruces y mutaciones.Rellenar genotipo: rellena el número especificado de genes en el genotipo de cada autómata.Conway: llena la población con máquinas de tipo Konveevsky.A continuación hay dos líneas: losnúmeros de las máquinas que se muestran.El contenido de la matriz fenotipo.El acervo genético de la población es aún más bajo.Todo el progreso se almacena en el almacenamiento local.Puedes jugar con rifles de asalto tipo Konveevsky (con los que se consideraron últimos en el artículo) aquí:4. Autómata de Conway y similares (2).
el botón Inicio inicia las máquinas.Stop - se detiene.Uno es una iteración.Borrar: detiene la máquina y llena el estado inicial de forma aleatoria.Borrar (1 celda): detiene la máquina y llena una celda en el estado inicial.Los botones restantes en esta línea cuentan el número especificado de iteraciones para cada autómata.Renderizar un autómata en lienzo consume todo el rendimiento. Si necesita calcular rápidamente 200 iteraciones, haga clic en Count 200. No hacemos clic en el botón Count 5000, el navegador puede colgarlo.Menos de 20 máquinas aleatorias (tamaño de la población - 200 máquinas). Debajo de las máquinas expendedoras casillas de verificación. Marcamos lo más interesante. Presione Seleccionar: el estado físico de la máquina aumentará en el número indicado a la derecha.Mutaciones: la probabilidad de mutaciones.Gens es el número de genes mutantes.Iniciar evolución: lanza el mecanismo de cruces y mutaciones.Rellenar genotipo: rellena el número especificado de genes en el genotipo de cada autómata.Conway: llena la población con máquinas de tipo Konveevsky.A continuación hay dos líneas: losnúmeros de las máquinas que se muestran.El contenido de la matriz fenotipo.El acervo genético de la población es aún más bajo.Todo el progreso se almacena en el almacenamiento local.Puedes jugar con rifles de asalto tipo Konveevsky (con los que se consideraron últimos en el artículo) aquí:4. Autómata de Conway y similares (2).