Bienvenido a una de las conferencias en CS231n: Redes neuronales convolucionales para el reconocimiento visual .

Contenido

• Descripción de la arquitectura
• Capas en una red neuronal convolucional
  - capa convolucional
  - Submuestreo de capa
  - Capa de normalización
  - capa completamente conectada
  - Convierta capas completamente conectadas en capas convolucionales
• Arquitectura de red neuronal convolucional
  - Plantillas de capa
  - Patrones de tamaño de capa
  - Estudio de caso (LeNet, AlexNet, ZFNet, GoogLeNet, VGGNet)
  - Aspectos computacionales
• Lectura adicional

Redes neuronales convolucionales (CNN / ConvNets)

Las redes neuronales convolucionales son muy similares a las redes neuronales habituales que estudiamos en el último capítulo (refiriéndose al último capítulo del curso CS231n): consisten en neuronas, que, a su vez, contienen pesos y desplazamientos variables. Cada neurona recibe algunos datos de entrada, calcula el producto escalar y, opcionalmente, utiliza una función de activación no lineal. La red completa, como antes, es la única función de evaluación diferenciable: desde el conjunto inicial de píxeles (imagen) en un extremo hasta la distribución de probabilidad de pertenecer a una clase particular en el otro extremo. Estas redes todavía tienen una función de pérdida (por ejemplo, SVM / Softmax) en la última capa (totalmente conectada), y todos los consejos y recomendaciones que se dieron en el capítulo anterior con respecto a las redes neuronales ordinarias también son relevantes para las redes neuronales convolucionales.

Entonces, ¿qué ha cambiado? La arquitectura de las redes neuronales convolucionales implica explícitamente la obtención de imágenes en la entrada, lo que nos permite tener en cuenta ciertas propiedades de los datos de entrada en la propia arquitectura de red. Estas propiedades le permiten implementar la función de distribución directa de manera más eficiente y reducir en gran medida el número total de parámetros en la red.

Descripción de la arquitectura

Recordamos las redes neuronales ordinarias. Como vimos en el capítulo anterior, las redes neuronales reciben datos de entrada (un solo vector) y los transforman "empujando" a través de una serie de capas ocultas . Cada capa oculta consta de un cierto número de neuronas, cada una de las cuales está conectada a todas las neuronas de la capa anterior y donde las neuronas de cada capa son completamente independientes de otras neuronas en el mismo nivel. La última capa completamente conectada se llama "capa de salida" y en problemas de clasificación es la distribución de calificaciones por clase.

Las redes neuronales convencionales no escalan bien para imágenes más grandes . En el conjunto de datos CIFAR-10, las imágenes tienen un tamaño de 32x32x3 (32 píxeles de alto, 32 píxeles de ancho, 3 canales de color). Para procesar dicha imagen, una neurona completamente conectada en la primera capa oculta de una red neuronal normal tendrá 32x32x3 = 3072 pesos. Esta cantidad aún es aceptable, pero se hace evidente que dicha estructura no funcionará con imágenes más grandes. Por ejemplo, una imagen más grande, 200x200x3, hará que el número de pesos se convierta en 200x200x3 = 120,000. Además, necesitaremos más de una neurona, por lo que el número total de pesos comenzará a crecer rápidamente. Se hace obvio que la conectividad es excesiva y una gran cantidad de parámetros conducirán rápidamente a la red a la reentrenamiento.

Representaciones 3D de neuronas . Las redes neuronales convolucionales utilizan el hecho de que los datos de entrada son imágenes, por lo que forman una arquitectura más sensible para este tipo de datos. En particular, a diferencia de las redes neuronales convencionales, las capas en la red neuronal convolucional organizan las neuronas en 3 dimensiones: ancho, altura, profundidad ( Nota : la palabra "profundidad" se refiere a la tercera dimensión de las neuronas de activación, y no a la profundidad de la red neuronal en sí medida en número de capas). Por ejemplo, las imágenes de entrada del conjunto de datos CIFAR-10 son datos de entrada en una representación 3D, cuya dimensión es 32x32x3 (ancho, alto, profundidad). Como veremos más adelante, las neuronas en una capa se asociarán con un pequeño número de neuronas en la capa anterior, en lugar de estar conectadas a todas las neuronas anteriores en la capa. Además, la capa de salida para la imagen del conjunto de datos CIFAR-10 tendrá una dimensión de 1 × 1 × 10, porque al acercarnos al final de la red neuronal reduciremos el tamaño de la imagen a un vector de estimaciones de clase ubicadas a lo largo de la profundidad (tercera dimensión).

Visualización:

Red neuronal estándar	Red neuronal convolucional

Lado izquierdo: red neuronal estándar de 3 capas.
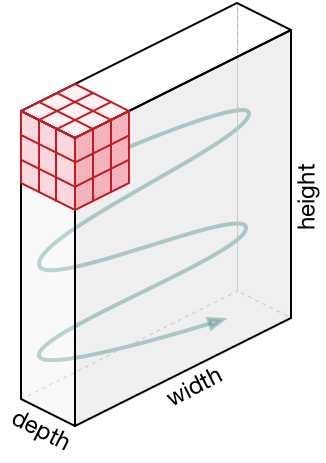
En el lado derecho: la red neuronal convolucional tiene sus neuronas en 3 dimensiones (ancho, alto, profundidad), como se muestra en una de las capas. Cada capa de red neuronal convolucional convierte una representación 3D de la entrada en una representación 3D de la salida como neuronas de activación. En este ejemplo, la capa de entrada roja contiene la imagen, por lo que su tamaño será igual al tamaño de la imagen y la profundidad será 3 (tres canales: rojo, verde, azul).

La red neuronal convolucional consiste en capas. Cada capa es una API simple: convierte la representación 3D de entrada en la representación 3D de salida de una función diferenciable, que puede contener o no parámetros.

Capas usadas para construir redes neuronales convolucionales

Como ya hemos descrito anteriormente, una red neuronal convolucional simple es un conjunto de capas, donde cada capa convierte una representación en otra utilizando una función diferenciable. Utilizamos tres tipos principales de capas para construir redes neuronales convolucionales: una capa convolucional , una capa de submuestreo y una capa totalmente conectada (lo mismo que usamos en una red neuronal normal). Organizamos estas capas secuencialmente para obtener la arquitectura SNA.

Ejemplo de arquitectura: descripción general. A continuación profundizaremos en los detalles, pero por ahora, para el conjunto de datos CIFAR-10, la arquitectura de nuestra red neuronal convolucional puede ser [INPUT -> CONV -> RELU -> POOL -> FC] . Ahora con más detalle:

• INPUT [32x32x3] contendrá los valores originales de los píxeles de la imagen, en nuestro caso la imagen tiene 32px de ancho, 32px de alto y 3 canales de color R, G, B.
• CONV capa CONV producirá un conjunto de neuronas de salida que se asociarán con el área local de la imagen fuente de entrada; cada una de esas neuronas calculará el producto escalar entre sus pesos y esa pequeña parte de la imagen original con la que está asociada. El valor de salida puede ser una representación 3D de 323212 , si, por ejemplo, decidimos usar 12 filtros.
• RELU capa RELU aplicará la función de activación del elemento max(0, x) . Esta conversión no cambiará la dimensión de datos - [32x32x12] .
• POOL capa POOL realizará la operación de muestreo de la imagen en dos dimensiones: altura y ancho, lo que como resultado nos dará una nueva representación 3D [161612] .
• FC capa FC (capa totalmente conectada) calculará las calificaciones por clases, la dimensión resultante será [1x1x10] , donde cada uno de los 10 valores corresponderá a las calificaciones de una clase particular entre 10 categorías de imágenes de CIFAR-10. Como en las redes neuronales convencionales, cada neurona de esta capa estará asociada con todas las neuronas de la capa anterior (representación 3D).

Así es como la red neuronal convolucional transforma la imagen original, capa por capa, desde el valor de píxel inicial hasta la estimación de clase final. Tenga en cuenta que algunas capas contienen opciones y otras no. En particular, las capas CONV/FC llevan a cabo una transformación, que no solo es una función que depende de los datos de entrada, sino que también depende de los valores internos de pesos y desplazamientos en las neuronas mismas. RELU/POOL capas RELU/POOL , RELU/POOL otro lado, usan funciones no parametrizadas. Los parámetros en las capas CONV/FC se entrenarán por gradiente descendente para que la entrada reciba las etiquetas de salida correctas correspondientes.

Para resumir:

• La arquitectura de la red neuronal convolucional, en su representación más simple, es un conjunto ordenado de capas que transforma la representación de una imagen en otra representación, por ejemplo, estimaciones de miembros de clase.
• Hay varios tipos diferentes de capas (CONV - capa convolucional, FC - completamente conectado, RELU - función de activación, POOL - capa de submuestra - el más popular).
• Cada capa de entrada recibe una representación 3D, la convierte en una representación 3D de salida utilizando una función diferenciable.
• Cada capa puede y no tener parámetros (CONV / FC - tiene parámetros, RELU / POOL - no).
• Cada capa puede y no tener hiperparámetros (CONV / FC / POOL - have, RELU - no)

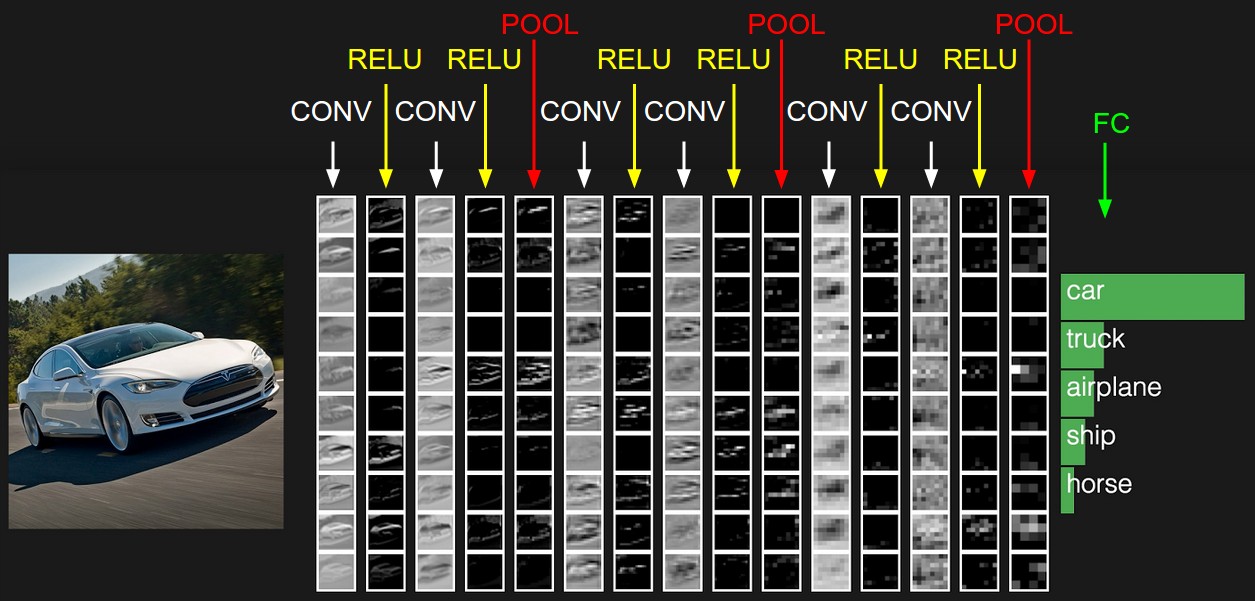
La representación inicial contiene los valores de píxeles de la imagen (a la izquierda) y estimaciones de las clases a las que pertenece el objeto en la imagen (a la derecha). Cada transformación de vista se marca como una columna.

Capa convolucional

La capa convolucional es la capa principal en la construcción de redes neuronales convolucionales.

Descripción general sin sumergirse en las características del cerebro. Primero intentemos averiguar qué sigue calculando la capa CONV sin sumergirnos y tocar el tema del cerebro y las neuronas. Los parámetros de la capa convolucional consisten en un conjunto de filtros entrenados. Cada filtro es una cuadrícula pequeña a lo largo del ancho y la altura, pero se extiende por toda la profundidad de la representación de entrada.

Por ejemplo, un filtro estándar en la primera capa de una red neuronal convolucional puede tener dimensiones de 5x5x3 (5px - ancho y alto, 3 - el número de canales de color). Durante un pase directo, movemos (para ser exactos: colapsamos) el filtro a lo largo del ancho y alto de la representación de entrada y calculamos el producto escalar entre los valores del filtro y los valores correspondientes de la representación de entrada en cualquier punto. En el proceso de mover el filtro a lo largo del ancho y alto de la representación de entrada, formamos un mapa de activación bidimensional que contiene los valores de aplicar este filtro a cada una de las áreas de la representación de entrada. Intuitivamente, queda claro que la red enseñará a los filtros a activarse cuando vean un cierto signo visual, por ejemplo, una línea recta en un cierto ángulo o representaciones en forma de rueda en niveles superiores. Ahora que hemos aplicado todos nuestros filtros a la imagen original, por ejemplo, había 12. Como resultado de la aplicación de 12 filtros, recibimos 12 tarjetas de activación de dimensión 2. Para producir una representación de salida, combinamos estas tarjetas (secuencialmente en la tercera dimensión) y obtenemos una representación dimensión [WxHx12].

Una visión general a la que conectamos el cerebro y las neuronas. Si eres fanático del cerebro y las neuronas, puedes imaginar que cada neurona "mira" una gran sección de la representación de entrada y transfiere información sobre esta sección a las neuronas vecinas. A continuación discutiremos los detalles de la conectividad neuronal, su ubicación en el espacio y el mecanismo para compartir parámetros.

Conectividad local. Cuando se trata de datos de entrada con una gran cantidad de dimensiones, por ejemplo, como en el caso de las imágenes, entonces, como ya hemos visto, no hay absolutamente ninguna necesidad de conectar las neuronas con todas las neuronas de la capa anterior. En cambio, solo conectaremos neuronas a áreas locales de la representación de entrada. El grado espacial de conectividad es uno de los hiperparámetros y se denomina campo receptivo (el campo receptivo de una neurona es del tamaño del mismo núcleo de filtro / convolución). El grado de conectividad a lo largo de la tercera dimensión (profundidad) siempre es igual a la profundidad de la representación original. Es muy importante enfocarse nuevamente en esto, prestar atención a cómo definimos las dimensiones espaciales (ancho y alto) y la profundidad: las conexiones neuronales son locales en ancho y alto, pero siempre se extienden a lo largo de toda la representación de entrada.

Ejemplo 1. Imagine que la representación de entrada tiene un tamaño de 32x32x3 (RGB, CIFAR-10). Si el tamaño del filtro (campo receptivo de la neurona) es 5 × 5, entonces cada neurona en la capa convolucional tendrá pesos en la región 5 × 5 × 3 de la representación original, lo que finalmente conducirá al establecimiento de 5 × 5 × 3 = 75 enlaces (pesos) + 1 parámetro de compensación. Tenga en cuenta que el grado de conexión en profundidad debe ser igual a 3, ya que esta es la dimensión de la representación original.

Ejemplo 2. Imagine que la representación de entrada tiene un tamaño de 16x16x20. Usando como ejemplo el campo receptivo de una neurona de tamaño 3x3, cada neurona de capa convolucional tendrá 3x3x320 = 180 conexiones (pesos) + 1 parámetro de desplazamiento. Tenga en cuenta que la conectividad es local en ancho y alto, pero completa en profundidad (20).

# 1	# 2

Desde el lado izquierdo: la representación de entrada se muestra en rojo (por ejemplo, una imagen de tamaño CIFAR-10 de 32x332) y un ejemplo de la representación de neuronas en la primera capa convolucional. Cada neurona en la capa convolucional está asociada solo con el área local de la representación de entrada, pero completamente en profundidad (en el ejemplo, a lo largo de todos los canales de color). Tenga en cuenta que hay muchas neuronas en la imagen (en el ejemplo - 5) y están ubicadas a lo largo de la 3ª dimensión (profundidad); a continuación se explicarán estas disposiciones.
En el lado derecho: las neuronas de la red neuronal aún permanecen sin cambios: todavía calculan el producto escalar entre sus pesos y datos de entrada, aplican la función de activación, pero su conectividad ahora está limitada por el área local espacial.

La ubicación espacial. Ya hemos descubierto la conectividad de cada neurona en la capa convolucional con la representación de entrada, pero aún no hemos discutido cuántas de estas neuronas o cómo están ubicadas. Tres hiperparámetros afectan el tamaño de la vista de salida: profundidad , paso y alineación .

1. La profundidad de la representación de salida es un hiperparámetro: corresponde a la cantidad de filtros que queremos aplicar, cada uno de los cuales aprende algo más en la representación original. Por ejemplo, si la primera capa convolucional recibe una imagen como entrada, entonces se pueden activar diferentes neuronas a lo largo de la tercera dimensión (profundidad) en presencia de diferentes orientaciones de líneas en un área determinada o grupos de un color determinado. Al conjunto de neuronas que "miran" la misma área de la representación de entrada, llamaremos la columna profunda (o "fibra" - fibra).
2. Necesitamos determinar el paso (tamaño de desplazamiento en píxeles) con el que se moverá el filtro. Si el paso es 1, entonces cambiamos el filtro por 1 píxel en una iteración. Si el paso es 2 (o, que se usa con menos frecuencia, 3 o más), el desplazamiento se produce por cada dos píxeles en una iteración. Un paso más grande da como resultado una representación de salida más pequeña.
3. Como veremos pronto, a veces será necesario complementar la representación de entrada a lo largo de los bordes con ceros. El tamaño de alineación (el número de columnas / filas rellenas con cero) también es un hiperparámetro. Una buena característica del uso de la alineación es el hecho de que la alineación nos permitirá controlar la dimensión de la representación de salida (a menudo mantendremos las dimensiones originales de la vista, preservando el ancho y la altura de la representación de entrada con el ancho y la altura de la representación de salida).

Podemos calcular la dimensión final de la representación de salida presentándola en función del tamaño de la representación de entrada ( W ), el tamaño del campo receptivo de las neuronas de la capa convolucional ( F ), el paso ( S ) y el tamaño de la alineación ( P ) en los bordes. Puede ver por sí mismo que la fórmula correcta para calcular el número de neuronas en la representación de salida es la siguiente (W - F + 2P) / S + 1 . Por ejemplo, para una representación de entrada de tamaño 7x7 y tamaño de filtro de 3x3, paso 1 y alineación 0, obtenemos una representación de salida de tamaño 5x5. En el paso 2, obtendríamos una representación de salida de 3x3. Veamos otro ejemplo, esta vez ilustrado gráficamente:

Ilustración de una disposición espacial. En este ejemplo, solo una dimensión espacial (eje x), una neurona con campo receptivo F = 3 , tamaño de representación de entrada W = 5 y alineación P = 1 . En el lado izquierdo : el campo receptivo de la neurona se mueve con un paso S = 1 , que como resultado da el tamaño de la representación de salida (5 - 3 + 2) / 1 + 1 = 5. En el lado derecho : la neurona usa el campo receptivo de tamaño S = 2 , que en el resultado es el tamaño de la representación de salida (5 - 3 + 2) / 2 + 1 = 3. Tenga en cuenta que el tamaño de paso S = 3 no se puede utilizar, ya que con este tamaño de paso el campo receptivo no capturará parte de la imagen. Si usamos nuestra fórmula, entonces (5 - 3 + 2) = 4 no es múltiplo de 3. Los pesos de las neuronas en este ejemplo son [1, 0, -1] (como se muestra en la imagen de la derecha), y el desplazamiento es cero. Estos pesos son compartidos por todas las neuronas amarillas.

Usando la alineación . Preste atención al ejemplo en el lado izquierdo, que contiene 5 elementos en la salida y 5 elementos en la salida. Esto funcionó porque el tamaño del campo receptivo (filtro) era 3 y utilizamos la alineación P = 1 . Si no hubiera alineación, entonces el tamaño de la representación de salida sería igual a 3, porque precisamente precisamente tantas neuronas encajarían allí. En general, establecer el tamaño de alineación P = (F - 1) / 2 con un paso igual a S = 1 le permite obtener el tamaño de la representación de salida similar a la representación de entrada. Un enfoque similar que usa la alineación a menudo se aplica en la práctica, y discutiremos las razones a continuación cuando hablemos sobre la arquitectura de las redes neuronales convolucionales.

Límites de tamaño de paso . Tenga en cuenta que los hiperparámetros responsables de la disposición espacial también están relacionados por limitaciones. Por ejemplo, si la representación de entrada tiene un tamaño de W = 10 , P = 0 y el tamaño del campo receptivo F = 3 , entonces es imposible usar un tamaño de paso igual a S = 2 , ya que (W - F + 2P) / S + 1 = (10 - 3 + 0) / 2 + 1 = 4.5 , que proporciona un valor entero del número de neuronas. Por lo tanto, dicha configuración de hiperparámetros se considera inválida y las bibliotecas para trabajar con redes neuronales convolucionales generarán una excepción, forzarán la alineación o incluso cortarán la representación de entrada. Como veremos en las siguientes secciones de este capítulo, la definición de los hiperparámetros de la capa convolucional sigue siendo un dolor de cabeza que puede reducirse mediante el uso de ciertas recomendaciones y "buenas reglas de tono" al diseñar la arquitectura de redes neuronales convolucionales.

Ejemplo de la vida real . Arquitectura de red neuronal convolucional Krizhevsky et al. , que ganó el concurso ImageNet en 2012, recibió 227x227x3 imágenes. En la primera capa convolucional, utilizó un campo receptivo de tamaño F = 11 , paso S = 4 y tamaño de alineación P = 0 . Como (227-11) / 4 + 1 = 55, y la capa convolucional tenía una profundidad de K = 96 , la dimensión de salida de la presentación fue 55x55x96. Cada una de las neuronas de 55x55x96 en esta representación se asoció con una región de tamaño 11x11x3 en la representación de entrada. Además, todas las 96 neuronas en la columna profunda están asociadas con la misma región 11x11x3, pero con diferentes pesos. Y ahora un poco de humor: si decide familiarizarse con el documento original (estudio), tenga en cuenta que el documento afirma que la entrada recibe imágenes de 224x224, lo que no puede ser cierto, porque (224 - 11) / 4 + 1 de ninguna manera dar un valor entero. Este tipo de situación a menudo se confunde para las personas en historias con redes neuronales convolucionales. Supongo que Alex usó el tamaño de alineación P = 3 , pero olvidó mencionar esto en el documento.

Opciones para compartir El mecanismo para compartir parámetros en capas convolucionales se usa para controlar el número de parámetros. Preste atención al ejemplo anterior, ya que puede ver que hay 55x55x96 = 290,400 neuronas en la primera capa convolucional y cada una de las neuronas tiene 11x11x3 = 363 pesos + 1 valor de compensación. En total, si multiplicamos estos dos valores, obtenemos 290400x364 = 105 705 600 parámetros solo en la primera capa de la red neuronal convolucional. ¡Obviamente, esto es de gran importancia!

Resulta que es posible reducir significativamente el número de parámetros haciendo una suposición: si alguna propiedad calculada en posición (x, y) nos importa, entonces esta propiedad calculada en posición (x2, y2) también nos importará. En otras palabras, denotando una "capa" bidimensional en profundidad como una "capa profunda" (por ejemplo, la vista [55x55x96] contiene 96 capas profundas, cada una de 55x55 de tamaño), construiremos neuronas en profundidad con los mismos pesos y desplazamiento. Con este esquema de compartir parámetros, la primera capa convolucional en nuestro ejemplo ahora contendrá 96 conjuntos únicos de pesos (cada conjunto para cada capa de profundidad), en total habrá 96x11x11x3 = 34,848 pesos únicos o 34,944 parámetros (+96 compensaciones). Además, todas las neuronas de 55x55 en cada capa profunda ahora usarán los mismos parámetros. En la práctica, durante la propagación hacia atrás, cada neurona en esta representación calculará el gradiente para sus propios pesos, pero estos gradientes se sumarán sobre cada capa de profundidad y actualizarán solo un conjunto único de pesos en cada nivel.

Tenga en cuenta que si todas las neuronas en la misma capa profunda usaran los mismos pesos, entonces para la propagación directa a través de la capa convolucional, se calcularía la convolución entre los valores de los pesos de las neuronas y los datos de entrada. Es por eso que es habitual llamar a un solo conjunto de pesos: un filtro (núcleo) .

Ejemplos de filtros que se obtuvieron al entrenar el modelo Krizhevsky et al. Cada uno de los 96 filtros que se muestran aquí tiene un tamaño de 11x11x3 y cada uno de ellos es compartido por todas las neuronas de 55x55 de una capa profunda. Tenga en cuenta que la suposición de compartir los mismos pesos tiene sentido: si la detección de una línea horizontal es importante en una parte de la imagen, entonces es intuitivamente claro que dicha detección es importante en otra parte de esta imagen. Por lo tanto, no tiene sentido volver a entrenar cada vez para encontrar líneas horizontales en cada uno de los 55x55 lugares diferentes de la imagen en la capa convolucional.

Debe tenerse en cuenta que la suposición de compartir parámetros no siempre tiene sentido. Por ejemplo, si una imagen con una estructura centrada se alimenta a la entrada de una red neuronal convolucional, donde nos gustaría poder aprender una propiedad en una parte de la imagen y otra propiedad en la otra parte de la imagen. Un ejemplo práctico son las imágenes de caras centradas. Se puede suponer que se pueden identificar diferentes signos oculares o capilares en diferentes áreas de la imagen, por lo tanto, en este caso, se usa relajación de pesas y la capa se denomina conectada localmente .

Numpy ejemplos . Las discusiones anteriores deben transferirse al plano de los detalles y a los ejemplos con código. Imagine que la representación de entrada es una matriz numpy de X Entonces:

• La columna profunda ( hilo ) en la posición (x,y) se representará como sigue X[x,y,:] .
• La capa profunda , o como la llamamos anteriormente, el mapa de activación en la profundidad d se representará de la siguiente manera X[:,:,d] .

Un ejemplo de una capa convolucional . , X X.shape: (11,11,4) . , P=1 , () F=5 S=1 . 44, — (11-5)/2+1=4. ( V ), ( ):

• V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
• V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
• V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
• V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

, numpy , * . , W0 b0 . W0 W0.shape: (5,5,4) , 5, 4. . , , 2 ( ). :

• V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
• V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
• V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
• V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
• V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1 (, y )
• V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1 (, )

— W1 b1 . , V . , , , ReLU , . .

. :

• W1 x H1 x D1
• 4 -:
  
  • K ,
  • F ,
  • S ,
  • P .
• W2 x H2 x D2 ,
  
  • W2 = (W1 — F + 2P)/S + 1
  • H2 = (H1 — F + 2P)/S + 1
  • D2 = K
• F x F x D1 , (F x F x D1) x K K .
• , d - ( W2 x H2 ) d - S d -.

- F = 3, S = 1, P = 1 . . " ".

. . 3D- ( — , — , — ), — . W1 = 5, H1 = 5, D1 = 3 , K = 2, F = 3, S = 2, P = 1 . , 33, 2. (5 — 3 + 2)/2 + 1 = 3. , , P = 1 . , () , .

( , html+css , )

. (). :

1. im2col . , 227x227x3 11113 4, 11113 = 363 . , 4 , (227 — 11) / 4 + 1 = 55 , X_col 3633025, 3025. , , , (), .
2. . , 96 11113, W_row 96363.
3. — np.dot(W_row, X_col) , . 963025.
4. 555596.

, , — , . , , — (, BLAS API). , im2col , .

. ( ) ( , ) ( - ). , .

11 . 11, Network in Network . , 11, , . , 2- , 11 ( ). , , 3- , . , 32323, 11, , , 3 (R, G, B — , ).

. - . . , . w 3 x : w[0] x[0] + w[1] x[1] + w[2] x[2] . 0. 1 : w[0] x[0] + w[1] x[2] + w[2] x[4] . "" 1 . , . , 2 33, , 55 ( 55 ). .

— . , , . , MAX. 22 2, 2 , 75% . MAX 22. . , :

• W1 x H1 x D1
• 2 -:
  
  • F ,
  • S ,
• W2 x H2 x D2 , :
  
  • W2 = (W1 — F)/S + 1
  • H2 = (H1 — F)/S + 1
  • D2 = D1
• ,
• (zero-padding ).

, : F=3, S=2 ( ), — F=2, S=2 . - .

. , , , L2-. , , .

#1	#2

. : 22422464 22 2, 11211264. , . : — (max-pooling), 2. 4 ( 22)

. , max(a,b) — . , ( ), .

. , . , : , . . , (VAEs) (GANs). , - , .

, , . , , . .

, . .

, , ( ). - , . , :

• , . , , , , , .
• , . , K=4096 ( ), 7712 - F=7, P=0, S=1, K=4096 . , 114096, .

. , . , 2242243 77512 ( AlexNet, , 5 , 7 — 224/2/2/2/2/2 = 7). AlexNet 4096 , , 1000 , . :

• , "" 77512, F=7 , 114096.
• F=1 , 114096.
• F=1 , 111000.

, , ( ) W . , "" () .

, 224224 , 77512 — 32 , 384384 1212512, 384/32 = 12. , , , 661000, (12 — 7)/1 + 1 = 6. , 111000 66 384384 .

( ) 384384, 224244 32 , , .

, , 36 , 36 . , , . .

, , 32 ? ( ). , 16 , 2 : 16 .

, , 3 : , ( , ) . ReLU , - . .

CONV-RELU-, POOL- , . - . , , . , :

 INPUT -> [[CONV -> RELU]*N -> POOL?] * M -> [FC -> RELU]*K -> FC 

* , POOL? . , N >= 0 ( N <= 3 ), M >= 0 , K >= 0 ( K < 3 ). , , :

• INPUT -> FC , . N = M = K = 0 .
• INPUT -> CONV -> RELU -> FC
• INPUT -> [CONV -> RELU -> POOL] * 2 -> FC -> RELU -> FC , .
• INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL] * 3 -> [FC -> RELU] * 2 -> FC . 2 . , , .

. 3 33 ( RELU , ). "" 33 . "" 33 , — 55. "" 33 , — 77. , 33 77. "" 77 ( ) , . -, , 3 , . -, C , , 77 (C(77)) = 49xxC , 33 3((33)) = 27 . , , . — , .

. , , Google, Microsoft. .

: , ImageNet. , , 90% . — " ": , , , ImageNet — , . .

-, . , :

( ) 2 . 32 (, CIFAR-10), 64, 96 (, STL-10), 224 (, ImageNet), 384 512.

(, 33 , 55), S=1 , , , . , F=3 P=1 . F=5, P=2 . F , P=(F-1)/2 . - ( 77), .

. 22 ( F=2 ) 2 ( S=2 ). , 75% (- , ). , , 33 ( ) 2 ( ). 33 , . .

. , , . , 1 , , .

1 ? . , 1 ( ), .

? , . , , , .

. ( ), , . , 64 33 1 2242243, 22422464. , , 10 , 72 ( , ). GPU, . , 77 2. , AlexNet, 1111 4.

. :

• LeNet . Yann LeCun 1990. LeNet , ZIP-, .
• AlexNet . , , Alex Krizhevsky, Ilya Sutskever Geoff Hinton. AlexNet ImageNet ILSVRC 2012 ( : 16% 26%). LeNet, , ( ).
• ZFNet . ILSVRC 2013 Matthew Zeiler Rob Fergus. ZFNet. AlexNet, -, .
• GoogLeNet . ILSVRC 2014 Szegedy et al. Google. Inception-, (4 60 AlexNet). , , . , — Inveption-v4.
• VGGNet . 2014 ILSVRC Karen Simonyan Andrew Zisserman, VGGNet. , . 16 + (33 22 ). . VGGNet — (140). , , , .
• ResNet . Residual- Kaiming He et al. ILSVRC 2015. . . ( 2016).

VGGNet . VGGNet . VGGNet , 33, 1 1, 22 2. ( ) :

 INPUT: [224x224x3] memory: 224*224*3=150K weights: 0 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*3)*64 = 1,728 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*64)*64 = 36,864 POOL2: [112x112x64] memory: 112*112*64=800K weights: 0 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*64)*128 = 73,728 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*128)*128 = 147,456 POOL2: [56x56x128] memory: 56*56*128=400K weights: 0 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*128)*256 = 294,912 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 POOL2: [28x28x256] memory: 28*28*256=200K weights: 0 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*256)*512 = 1,179,648 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 POOL2: [14x14x512] memory: 14*14*512=100K weights: 0 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 POOL2: [7x7x512] memory: 7*7*512=25K weights: 0 FC: [1x1x4096] memory: 4096 weights: 7*7*512*4096 = 102,760,448 FC: [1x1x4096] memory: 4096 weights: 4096*4096 = 16,777,216 FC: [1x1x1000] memory: 1000 weights: 4096*1000 = 4,096,000 TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd) TOTAL params: 138M parameters 

, , ( ) , . 100 140 .

. GPU 3/4/6 , GPU — 12 . , :

• : , ( ). , . , .
• : , , . , , 3 .
• , , ..

(, ), . , 4 ( 4 , — 8), 1024 , , . " ", , .

… call-to-action — , share :)
YouTube
Telegrama
VKontakte