⛅️ 🔬 😈 El mundo de la hiperesfera tridimensional. Trazado de rayos geodésicos en un universo cerrado con geometría esférica 🕑 🔨 🤹🏽

¿Te gustaría ver el mundo a través de los ojos de una criatura que vive en un universo cerrado compacto con geometría esférica? ¿Ves el mundo sin una noche? ¿Un mundo donde el otro polo del planeta es visible en el cielo? ¿Un mundo donde no hay diferencia entre un eclipse solar y un eclipse lunar? ¡Bienvenido a cat!

Introduccion Mundo cerrado bidimensional

Para comprender mejor lo que sucederá después, imagina que eres un ser bidimensional y vives en un mundo bidimensional que representa una esfera. ¿Cómo percibirás tu mundo? Comencemos por determinar la posición de los cuerpos. Puede declarar el punto en el que se encuentra el "centro del universo", seleccionar dos vectores unitarios mutuamente perpendiculares y utilizar el sistema de coordenadas cartesianas resultante en la vecindad del "centro del universo".

Sin embargo, a medida que te alejas del "centro del universo", cosas extrañas comenzarán a suceder. Lo que percibes como líneas perpendiculares, con una cierta distancia desde el "centro del universo" se convierte en lo que percibes como líneas paralelas ...

... Y las líneas paralelas se cruzan.

La razón es simple: lo que percibes como una línea recta es en realidad un círculo grande : la línea geodésica de la esfera. Por lo tanto, el sistema de coordenadas cartesianas no es adecuado para determinar la posición de los cuerpos en su mundo: cuando se aleja del "centro del universo" pierde su significado.

Tendrá que elegir otro, más adecuado para usar en su mundo, sistema de coordenadas - polar . Este sistema de coordenadas es natural y consistente. De hecho, el ángulo entre el eje polar y la dirección hacia el cuerpo permanece constante independientemente de la distancia al cuerpo.

Al poder determinar la posición de los cuerpos, podemos explorar mentalmente su mundo y describir algunos efectos que aparecen cuando se aleja del "centro del universo" y debido al hecho de que su mundo es una esfera.

La perspectiva inversa . Por lo general, cuando un cuerpo se aleja del "centro del universo", su tamaño angular disminuye. Sin embargo, a una distancia de más de un cuarto de la longitud de la línea geodésica desde el "centro del universo" con la extracción del cuerpo, su tamaño angular aumentará. Este efecto se debe al hecho de que la distancia entre las líneas geodésicas de la esfera y el ecuador aumenta, y después de que el ecuador disminuye. Un cuerpo remoto a la misma distancia del ecuador tendrá el mismo tamaño angular, independientemente de qué lado se encuentre del ecuador. Y este tamaño angular será mayor que el tamaño angular del cuerpo en el ecuador.

Estirando el cuerpo por todo el cielo. Aquí el término cielo completo se usa en significado: todo el campo de visión de un ser bidimensional (superior e inferior o frontal y posterior). Si el cuerpo está cerca del punto opuesto al "centro del universo", entonces, donde quiera que mire, encontrará su mirada con este cuerpo. El cuerpo no tendrá un punto que no se pueda ver: cada punto tiene un lugar en el cielo. Este es el último caso del efecto de perspectiva inversa.

Transformación simétrica tel. Si el cuerpo está a una distancia de más de la mitad de la longitud de la línea geodésica desde el "centro del universo", verá que este cuerpo se transforma simétricamente: los lados izquierdo y derecho del cuerpo cambiarán de lugar. Por lo general, los rayos izquierdo y derecho emitidos desde el "centro del universo" caen en los lados izquierdo y derecho del cuerpo. Sin embargo, a una distancia de la mitad de la longitud de la línea geodésica desde el "centro del universo", los rayos se cruzan y después del cruce caen en los lados opuestos del cuerpo.

La segunda perspectiva hacia adelante y hacia atrás. Este efecto también se observa si el cuerpo está a una distancia mayor que la mitad de la longitud de la línea geodésica desde el "centro del universo". A distancias de la mitad a las tres cuartas partes de la longitud de la línea geodésica desde el "centro del universo", con la eliminación del cuerpo, su tamaño angular disminuirá nuevamente (perspectiva directa). A distancias de tres cuartos a la longitud completa de la línea geodésica desde el "centro del universo", a medida que el cuerpo se aleja, su tamaño angular aumentará nuevamente (perspectiva inversa). Este efecto, así como el efecto de perspectiva inversa, está asociado con un cambio en la distancia entre las líneas geodésicas de la esfera: en el camino de regreso al "centro del universo", la distancia entre las líneas geodésicas de la esfera y el ecuador aumenta y disminuye después del ecuador.

Dobles Cada cuerpo en tu mundo tendrá un doble: si ves un cuerpo frente a ti, al darte la vuelta puedes ver su lado opuesto (doble). Un rayo emitido a lo largo de un largo camino recorre su mundo y entra en la parte posterior del cuerpo. Cabe señalar que la superficie del doble será esa parte de la superficie que no ves frente a ti, y se transformará simétricamente. Aquí, el término superficie se usa en el significado: el límite de un cuerpo bidimensional percibido por un ser bidimensional, aplicado a un círculo, en realidad es un arco circular percibido por un ser bidimensional como un segmento, sin embargo, para mayor claridad, destacaremos no solo el arco, sino también la parte del círculo que se encuentra detrás de él.

El paso del cuerpo a través de un punto opuesto al "centro del universo". Dado que el efecto de estirar el cuerpo hacia todo el cielo es muy inusual, lo consideraremos con más detalle. En las figuras: la vecindad de un punto opuesto al "centro del universo".

Se ve que:

primero, la superficie del cuerpo frente a ti aumenta (pintada en azul), y la que está detrás de ti disminuye (pintada en azul); al mismo tiempo, ambas superficies tienen las mismas dimensiones angulares, es decir, la superficie del cuerpo ubicada frente a usted se contrae (la mayor parte de la superficie se encuentra dentro de cada grado) y la que se encuentra detrás de usted se estira (la parte más pequeña de la superficie se encuentra dentro de cada grado)
cuando el cuerpo toca un punto opuesto al "centro del universo", el tamaño angular de ambas superficies es de 180 grados: la mitad del cielo (frente a usted) ocupa toda la superficie del cuerpo, y la segunda mitad del cielo (detrás de usted) está ocupada por un punto que se encuentra en la parte posterior del cuerpo
mientras el centro del cuerpo está alineado con el punto opuesto al "centro del universo", el proceso de tirar y estirar hacia atrás
cuando el cuerpo está ubicado en un punto opuesto al "centro del universo", su superficie no se distorsiona y se extiende sobre todo el cielo
el cuerpo deslizándose desde un punto opuesto al "centro del universo" se ve similar

Doble horizonte Imagina que vives en un planeta bidimensional. Mirando hacia abajo, ves la superficie de tu lado del planeta, y mirando hacia arriba, ves ... la superficie de la parte posterior del planeta. Además, estará muy apretado: puedes ver la superficie de la parte posterior del planeta y la parte de la superficie de tu lado del planeta que está detrás de tu espalda detrás del horizonte; puedes ver todo esto por encima de tu cabeza. El cielo se presentará en forma de una franja estrecha como un hilo, intercalada desde arriba y desde abajo por los horizontes de tu y los lados reverso del planeta. Esta es una combinación del efecto de estirar el cuerpo sobre todo el cielo y el efecto de un doble. En general, en su mundo, si nada obstaculiza su mirada, puede ver su nuca justo frente a usted ... una nuca tan saludable, en todos sus detalles ... se extiende por todo el cielo)

Un mundo sin noche. Imagina que el planeta bidimensional en el que vives gira en torno a una estrella bidimensional. La luz emitida por una estrella en un camino corto cae en el lado diurno del planeta. Al mismo tiempo, la luz emitida por una estrella a lo largo de un largo camino rodea tu mundo y cae en el lado nocturno del planeta. La noche ya no existe. Todo lo que queda son puestas de sol y amaneceres que ocurrirán simultáneamente: cuando el lado de la estrella que está frente a ti comienza a ir más allá del horizonte, el lado posterior de la estrella comenzará a levantarse detrás de ti desde detrás del horizonte. Por supuesto, puede resaltar la verdadera puesta de sol y el amanecer a lo largo del camino por el que pasó la luz, pero será casi imposible distinguirlos de los dobles.

También hay un caso extremo. Si el planeta tiene mala suerte y está en el punto de la estrella opuesta, entonces la estrella se extenderá a todo el cielo, pero será problemático admirarlo, ya que toda la luz emitida por la estrella caerá sobre el planeta (en ausencia de absorción de luz y dispersión por el medio interplanetario).

Eclipses solares y lunares. Imagine que un satélite natural bidimensional gira en torno a un planeta bidimensional en el que vive. Cuando un satélite se convierte entre un planeta y una estrella, su sombra cae sobre el planeta. Por otro lado, al mismo tiempo, el planeta se convierte entre la luz emitida por la estrella a lo largo de un largo camino y el satélite, es decir, la sombra del planeta cae sobre el satélite. Se produce un eclipse solar y lunar simultáneo. Por supuesto, es posible distinguir los verdaderos eclipses solares y lunares a lo largo del camino por el que pasó la luz, pero será prácticamente imposible distinguirlos de los gemelos. Caer en la sombra que cae sobre el planeta y su satélite durante los eclipses es la única forma de estar en la oscuridad en su mundo)

Mundo cerrado tridimensional

Arriba, examinamos el maravilloso mundo de un ser bidimensional. ¿Qué hay de nosotros los seres tridimensionales? ¿Cuál es la geometría del universo ? Desafortunadamente, la ciencia aún no puede responder esta pregunta. Principalmente las propiedades y el tamaño del Universo interfieren. Intentemos ayudar a la ciencia. Seleccionamos como candidato el universo cerrado más interesante con geometría esférica y lo examinamos visualmente. ¿Habrá efectos descubiertos por nosotros para un análogo bidimensional? ¿Quizás aprenderemos algo nuevo? ¿Algo que no esperabas saber? ¿O incluso ver lo que vemos todos los días, pero no le prestamos atención? ¿Cómo será un universo así?

Modelo

Exploraremos el mundo, que es una hiperesfera tridimensional (3 esferas), es decir, una esfera situada en un espacio de cuatro dimensiones. Elegimos un tipo de objetos para la visualización: una esfera (una esfera 2 que pertenece a una esfera 3).

Conceptos básicos y relaciones

Coordenadas cartesianas en un espacio de cuatro dimensiones : las designaremos como

$(x_0, x_1, x_2, x_3)$ - esto es en realidad

$(x, y, z, w)$ .

Coordenadas hipersféricas en un espacio de cuatro dimensiones (solo usamos ángulos, ya que el radio de nuestro mundo será constante): los denominaremos como

$(a_0, a_1, a_2)$ - esto es en realidad

$(\ phi, \ theta, \ psi)$ .

3 esferas centradas en el origen : un conjunto de puntos cuyo radio vector tiene una longitud igual al radio de las 3 esferas

$R$ Es nuestro mundo

$\ quad \ quad x_0 ^ 2 + x_1 ^ 2 + x_2 ^ 2 + x_3 ^ 2 = R ^ 2$

2 esferas que pertenecen a las 3 esferas : un conjunto de puntos cuyo radio vector tiene una longitud igual al radio de las 3 esferas

$R$ y se forma con el vector de radio del centro de la esfera 2

$c$ ángulo igual al radio angular de la esfera 2

$r_a$ Son nuestros objetos de visualización

$\ quad \ quad x_0 c_0 + x_1 c_1 + x_2 c_2 + x_3 c_3 = R ^ 2 \ cos r_a$

donde

$\ quad \ quad r_a = r / R$

$\ quad \ quad r$ - radio geodésico de una esfera de 2

Radio geodésico, angular y condicional : para comprender mejor qué es, considere un análogo bidimensional de una esfera 2 que pertenece a una esfera 3: un círculo que pertenece a una esfera.

El arco rojo en la figura es el radio geodésico del círculo.

$r$ . La esquina roja en el lado derecho de la figura es el radio angular del círculo.

$r_a = r / R$ . La altura del triángulo en el lado derecho de la figura es el radio condicional del círculo.

$r_n = R \ sin r_a$ .

Transición desde coordenadas hipersféricas

$(a_0, a_1, a_2)$ a cartesiano

$(x_0, x_1, x_2, x_3)$

$\ quad \ quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ quad \ quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ quad \ quad x_2 = R \ sin a_2 \ cos a_1$

$\ quad \ quad x_3 = R \ cos a_2$

donde

$\ quad \ quad a_0$ varía de

$0$ antes

$2 \ pi$

$\ quad \ quad a_1$ varía de

$0$ antes

$\ pi$

$\ quad \ quad a_2$ varía de

$0$ antes

$\ pi$

La intersección de la línea geodésica de una esfera 3 con una esfera 2 que pertenece a una esfera 3.
Esta relación se usará para el trazado de rayos. Que haya una línea geodésica que se extienda desde el polo de la 3-esfera.

$(0, 0, 0, R)$ en la dirección definida por los ángulos

$a_0$ y

$a_1$ - estos ángulos coinciden con los ángulos que determinan la dirección en el espacio tridimensional en la vecindad del polo de 3 esferas

$(0, 0, 0, R)$

$\ quad \ quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ quad \ quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ quad \ quad x_2 = R \ sin a_2 \ cos a_1$

$\ quad \ quad x_3 = R \ cos a_2$

simplificando tenemos (1)

$\ quad \ quad x_0 = r_0 \ sin a_2$

$\ quad \ quad x_1 = r_1 \ sin a_2$

$\ quad \ quad x_2 = r_2 \ sin a_2$

$\ quad \ quad x_3 = r_3 \ cos a_2$

donde

$\ quad \ quad r_0 = R \ sin a_1 \ cos a_0$

$\ quad \ quad r_1 = R \ sin a_1 \ sin a_0$

$\ quad \ quad r_2 = R \ cos a_1$

$\ quad \ quad r_3 = R$

sustituyendo (1) en la ecuación de la esfera 2 y simplificando tenemos (2)

$\ quad \ quad A \ sin a_2 + B \ cos a_2 = C$

donde

$\ quad \ quad A = r_0 c_0 + r_1 c_1 + r_2 c_2$

$\ quad \ quad B = r_3 c_3$

$\ quad \ quad C = R ^ 2 \ cos r_a$

sustituyendo (1) en la ecuación de la esfera 3 y simplificando tenemos (3)

$\ quad \ quad D \ sin ^ 2 a_2 + E \ cos ^ 2 a_2 = F$

donde

$\ quad \ quad D = r_0 ^ 2 + r_1 ^ 2 + r_2 ^ 2$

$\ quad \ quad E = r_3 ^ 2$

$\ quad \ quad F = R ^ 2$

expresando desde (2)

$\ cos a_2$ tenemos

$\ quad \ quad \ cos a_2 = (C - A \ sin a_2) / B$

sustituyendo en (3)

$\ cos a_2$ tenemos

$\ quad \ quad D \ sin ^ 2 a_2 + E / B ^ 2 (C - A \ sin a_2) ^ 2 = F$

simplificando tenemos

$\ quad \ quad a \ sin ^ 2 a_2 + b \ sin a_2 + c = 0$

donde

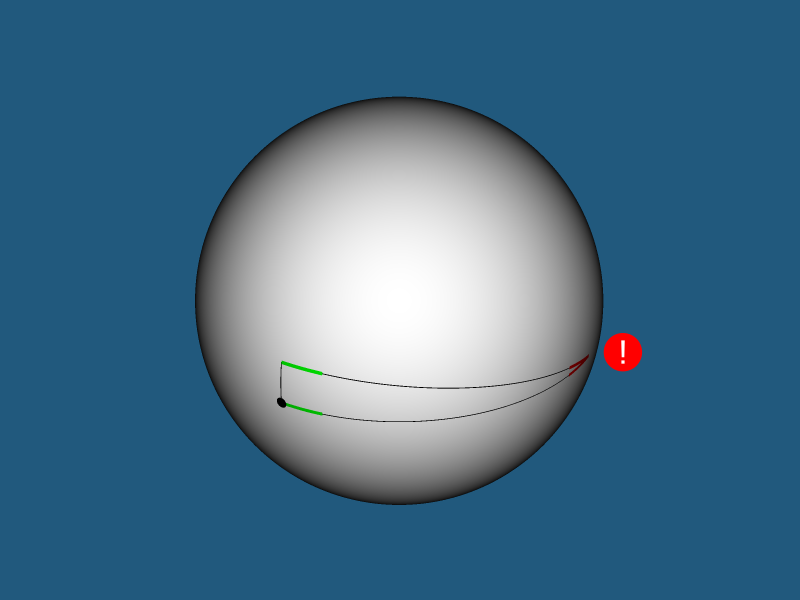
$\ quad \ quad m = E / B ^ 2$

$\ quad \ quad a = m A ^ 2 + D$

$\ quad \ quad b = -2 m A C$

$\ quad \ quad c = m C ^ 2 - F$

Un punto en la continuación de la línea geodésica de una esfera 3 que pasa por dos puntos.
Esta relación se utilizará para encontrar las coordenadas de textura y la normalidad externa en un punto arbitrario de la esfera 2 que pertenece a la esfera 3. Dejar

$\ quad \ quad O$ - centro de 3 esferas

$\ quad \ quad A$ - centro de la 2-esfera

$\ quad \ quad B$ Es un punto arbitrario de la 2-esfera.

$\ quad \ quad C$ - el punto deseado que se encuentra en la continuación de la línea geodésica

$AB$ a una pequeña distancia angular

$\ delta$ desde el punto

$B$

$\ quad \ quad D$ - punto de intersección de líneas

$AB$ y

$OC$

$\ quad \ quad E$ - el punto de intersección de la línea que pasa por el punto

$D$ perpendicular a recta

$AB$ y una línea que pasa por un punto

$O$ paralela a recta

$AB$

$\ quad \ quad r_a$ - radio angular de una esfera de 2

$\ quad \ quad a = (\ pi - r_a) / 2$

$\ quad \ quad b = a - \ delta$
Si

$r_a> \ pi$ entonces se debe poner

$r_a = 2 \ pi - r_a$ y

$\ delta = - \ delta$
Encontrara

$\ vec {OD}$

$\ quad \ quad \ vec {OD} = \ vec {OA} + \ vec {AB} / | \ vec {AB} | \ cdot | \ vec {AD} |$

donde

$\ quad \ quad | \ vec {AD} | = | \ vec {AB} | / 2 + | \ vec {OE} |$

$\ quad \ quad | \ vec {OE} | = | \ vec {DE} | / \ tan b$

$\ quad \ quad | \ vec {DE} | = R \ sin a$

encontrará

$\ vec {OC}$

$\ quad \ quad \ vec {OC} = \ vec {OD} / | \ vec {OD} | \ cdot R$

Iluminación

Utilizaremos dos modelos de iluminación.

Modelo de iluminación simple. En este modelo, el brillo de un punto de superficie depende del coseno del ángulo entre la normal externa a la superficie y la dirección al observador. Lo usaremos al construir imágenes para material explicativo. De hecho, este es un modelo con una fuente de luz puntual ubicada donde se encuentra el observador, en el que el brillo de un punto de superficie no depende de la distancia a la fuente de luz.

Modelo de iluminación realista. Este modelo tendrá una fuente puntual de luz dedicada. Lo usaremos cuando construyamos imágenes realistas. Este modelo puede tener en cuenta la influencia del área del frente de onda en el brillo de un punto de superficie (de hecho, la influencia de la distancia a la fuente de luz). En un universo cerrado con geometría esférica, el área del frente de onda es directamente proporcional al cuadrado del radio condicional de la esfera con un radio geodésico igual a la distancia desde el punto de la superficie hasta la fuente de luz. Con la distancia desde la fuente de luz, el área del frente de onda al ecuador aumenta (los rayos de luz divergen), y después de que el ecuador disminuye (los rayos de luz convergen, enfoque). Después de pasar el punto opuesto al "centro del universo", se produce el proceso inverso: los rayos de luz primero divergen y luego convergen nuevamente. Además, este modelo puede tener en cuenta las peculiaridades de percepción ( ley de Weber-Fechner ).

Para construir la imagen, utilizaremos el trazado de rayos inverso . Para que el modelo sea interactivo (examinaremos nuestro mundo y nos moveremos en él), la imagen debe construirse en tiempo real. Por lo tanto, realizaremos los cálculos en el sombreador de fragmentos (usamos WebGL). Implementamos la interfaz en JavaScript.

Texturas

Texture earth.jpg desde aquí

Textura moon.jpg desde aquí

Texture sun.png desde aquí

Primer conocido

Crearemos un mundo cerrado tridimensional con una longitud de línea geodésica de 100, por lo que nos será más fácil navegar: el ecuador de nuestro mundo estará ubicado a una distancia de 25 (un cuarto de la longitud de la línea geodésica) y el polo opuesto de nuestro mundo, a una distancia de 50 (la mitad de la longitud de la línea geodésica). Colocamos un planeta en nuestro mundo y pintamos partes de su superficie en colores según el octante en el que se encuentren:

Octante	Signo X	Signo Y	Signo z	Color
Yo	+	+	+	Rojo ( R ed)
II	-	+	+	Verde ( G reen)
III	-	-	+	Azul (azul)
IV	+	-	+	Naranja
V	+	+	-	Azul ( C yan)
VI	-	+	-	Púrpura ( M agenta)
VII	-	-	-	Amarillo (amarillo)
VIII	+	-	-	Blanco

Como textura principal, utilizaremos la textura de un tablero de ajedrez de 3x6, es decir, cada paralelo y meridiano atravesará exactamente 12 celdas. Como textura alternativa usaremos la textura del globo. A continuación se muestran imágenes de un sobrevuelo de familiarización de nuestro planeta.

Una instantánea del Polo Norte. El eje X se dirige hacia la derecha, el eje Y se dirige hacia arriba, el eje Z se dirige hacia nosotros. Al aplicar una textura alternativa, puede ver:

a la derecha está el Océano Pacífico
Arriba - Norteamérica
izquierda - el Océano Atlántico
abajo - Eurasia

Imágenes del vuelo desde el Polo Norte hacia el ecuador y desde el ecuador hasta el Polo Sur.

Instantánea del Polo Sur. El eje X se dirige hacia la derecha, el eje Y se dirige hacia abajo, el eje Z se aleja de nosotros. Al aplicar una textura alternativa, puede ver:

Derecha - Océano Pacífico, Nueva Zelanda, Australia
desde arriba - Océano Índico
izquierda - Océano Atlántico, África
abajo - América del Sur

Estudio visual

Realizaremos un estudio visual de nuestro mundo para descubrir análogos de los efectos que descubrimos en un mundo cerrado bidimensional.

Dobles Como en el análogo bidimensional, cada cuerpo en nuestro mundo tendrá un doble: si vemos el Polo Norte frente a nosotros, al dar la vuelta podemos ver ... el Polo Sur. La contracción de la superficie del doble es notable debido al hecho de que estamos lo suficientemente cerca del planeta.

Un experimento en el que el observador se aleja del planeta (la figura en la esquina superior izquierda de cada imagen es la distancia entre el observador y el planeta).

Se ve que:

inicialmente el tamaño angular del planeta disminuye; esta es la perspectiva directa habitual
entonces, cuando el planeta ha pasado el ecuador de nuestro mundo (distancia de más de 25), su tamaño angular aumenta; este es el efecto de la perspectiva opuesta que nos es familiar.
cuando nos arrastramos hacia el polo opuesto de nuestro mundo, vemos una superficie restringida (distancia 46.875)
cuando el planeta está en el polo opuesto de nuestro mundo (distancia 50) se extiende a todo el cielo
al deslizarnos desde el polo opuesto de nuestro mundo, vemos una superficie estirada (distancia 53.125)
después de que el planeta ha pasado el polo opuesto de nuestro mundo, se ve simétricamente transformado: el octante rojo ha cambiado con el azul, etc.
luego, el tamaño angular del planeta disminuye (distancia de 50 a 75), y luego aumenta (distancia de 75 a 100) - este es el efecto familiar de las segundas perspectivas hacia adelante y hacia atrás

Artefactos. Al usar el modelo, se notó que durante el paso del planeta a través de los puntos que se encuentran desde el observador a distancias de 25, 50 y 75, pueden aparecer artefactos: la lana puede "crecer" en el planeta o incluso puede "desmoronarse". Al parecer, mis matemáticas no tienen en cuenta algo)

Una imagen del planeta en las proximidades del polo opuesto de nuestro mundo (se utilizó una "lente" gran angular). La superficie del planeta frente a nosotros está muy estrecha: puedes ver no solo todo el hemisferio norte, sino también parte del hemisferio sur detrás del ecuador. La superficie del planeta detrás de nosotros está muy estirada: el Polo Sur es visible de manera prominente. Ambas superficies se estiran una hacia la otra, tratando de encerrarnos en una concha esférica y revelarnos una imagen de un planeta extendido a través del cielo.

Un experimento en el que el observador mira hacia arriba (el número en la esquina superior izquierda de cada imagen es el ángulo entre la dirección hacia abajo y la mirada).

En las fotos:

primero aparece el horizonte de nuestro lado del planeta
luego, vemos un segundo horizonte sobre él, donde encontramos lo que está ubicado en nuestro lado del planeta detrás de nuestra espalda detrás del horizonte
mirando hacia arriba, vemos la parte posterior del planeta

Imagen de doble horizonte (se utiliza "lente" gran angular). La franja del cielo es lo suficientemente grande porque estamos a una altitud de unos 50 km.

Una imagen del cielo sobre la cabeza (se utilizó una "lente" gran angular).

Un mundo sin noche.
Además, por simplicidad, llamaremos a nuestro planeta Tierra, su satélite natural, la Luna, y la estrella alrededor de la cual giran, el Sol. No se observarán las proporciones de los tamaños del Sol, la Tierra, la Luna y sus órbitas para mayor claridad.
En la imagen: la frontera entre los lados diurno y nocturno del planeta que pasa por el Océano Atlántico. Al mismo tiempo, la Tierra menguante y en crecimiento son visibles. Los muchachos sentados en las bases lunares de nuestro mundo ven una imagen aproximadamente similar)

En animación: el movimiento de la frontera entre los lados diurno y nocturno de la Tierra. Puedes ver la superposición del Sol por el disco de la Tierra iluminado por los rayos del Sol liberados a lo largo de un largo camino.

Eclipses solares y lunares.
En la imagen: la luna emerge de la sombra de la Tierra. Los límites entre el día y la noche de la Tierra y la Luna son visibles.

En animación: eclipses solares y lunares.

Se ve que:

primero, la tierra proyecta una sombra sobre la luna, y la luna proyecta una sombra sobre la tierra
entonces la luna sale de la sombra de la tierra, y la sombra de la luna deja la superficie de la tierra
entonces la sombra de la luna vuelve a la superficie de la tierra y la luna vuelve a entrar en la sombra de la tierra
el límite entre los lados diurno y nocturno de la luna no es visible cuando la luna está cubierta por el disco de la Tierra porque el lado de la luna que está frente a nosotros todavía está a la sombra de la Tierra

En la animación: el movimiento de los límites entre los lados diurno y nocturno de la Tierra y la Luna combinados con eclipses solares y lunares. Los chicos que sirven a los observatorios en el punto L _{2 de} Lagrange en nuestro mundo ven aproximadamente la misma imagen) Por supuesto, si descuidamos la rotación de la Tierra)

Foto: amanecer en la ISS en nuestro mundo)

Conclusión

¿Para qué es todo esto? Realmente quería ver el mundo a través de los ojos de una criatura que vivía en un universo compacto y cerrado con geometría esférica. Conocer este maravilloso mundo sin los símbolos de Christoffel y cosas similares, sin dejar de estar dentro del marco del curso general de las matemáticas superiores. El resultado está delante de ti. Todo parece funcionar. ¡Espero que hayas tenido un día interesante y agradable!

Código fuente

Modelo de trabajo (abierto en PC, no para dispositivos móviles).

Para aquellos que estén interesados en el tema, hay un magnífico artículo que habla sobre los sorprendentes fenómenos que se pueden observar en el Universo real: cómo dibujar un agujero negro. Trazado de rayos geodésicos en espacio-tiempo curvo .

El mundo de la hiperesfera tridimensional. Trazado de rayos geodésicos en un universo cerrado con geometría esférica

Introduccion Mundo cerrado bidimensional

Mundo cerrado tridimensional

Modelo

Primer conocido

Estudio visual

Conclusión

More articles: