Logística de la acción para la recogida selectiva de reciclables.

En lugar de unirse

Cuando los procesos de recolección y procesamiento de desechos se ajustan completamente en Rusia, no es fácil decirlo, pero no quiero participar en la reposición de los vertederos ahora. Por lo tanto, en muchas ciudades grandes, de una forma u otra, hay movimientos de voluntarios que participan en una recolección particular por separado.

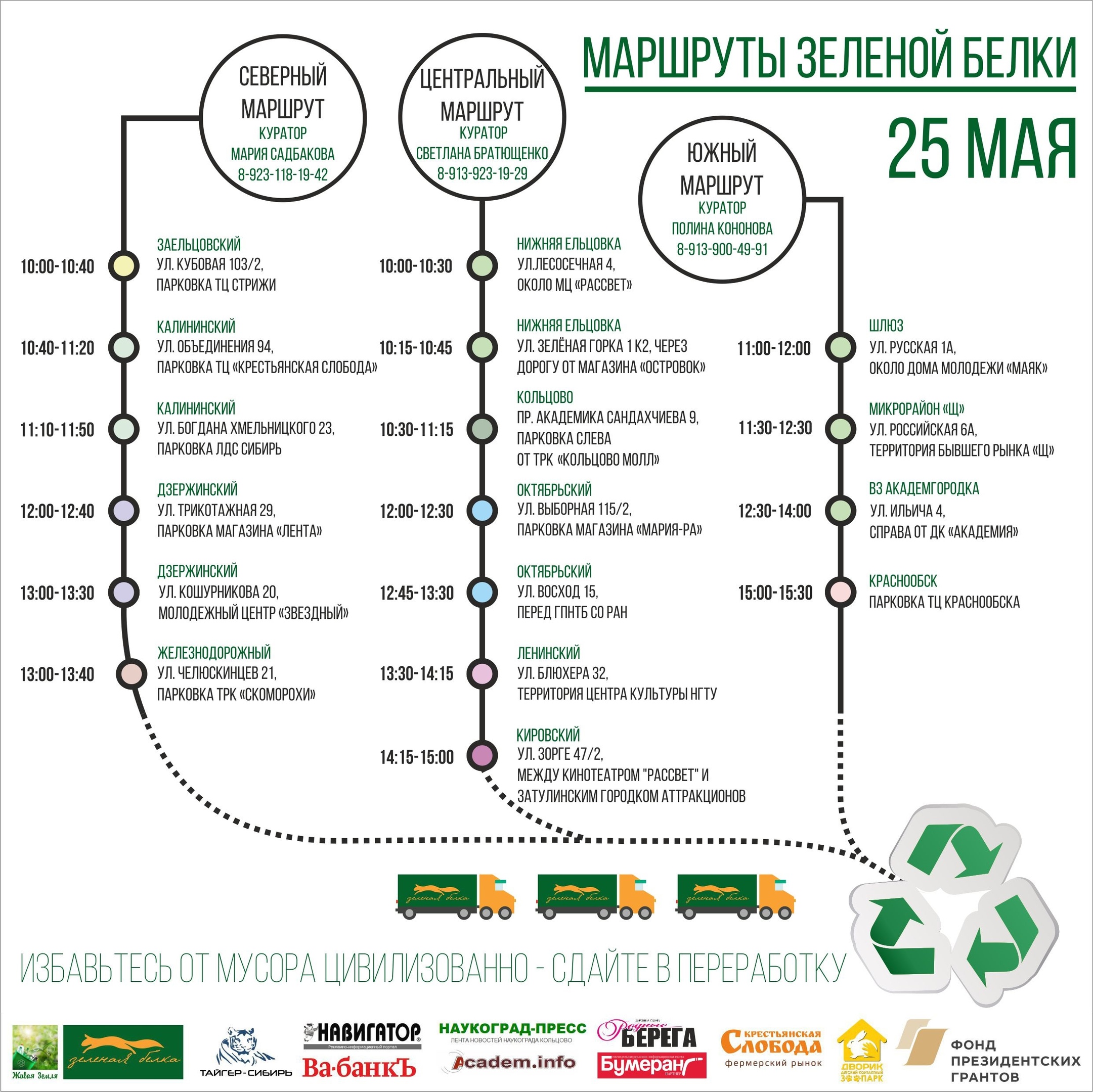
En Novosibirsk, dicha actividad se forma alrededor de la campaña Ardilla verde, en la que una vez al mes, la gente del medio ambiente lleva los desechos domésticos reciclables acumulados a lugares predeterminados en un momento determinado. Al mismo tiempo, llega un camión alquilado, que lleva los materiales reciclables recogidos y ordenados al sitio, desde donde se redistribuye entre varias empresas de procesamiento. La acción ha existido desde 2014, y desde entonces el número de puntos de recolección de materiales reciclables, así como sus volúmenes, ha aumentado significativamente. Para el enrutamiento de camiones, solo una mirada no fue suficiente, y comenzamos a desarrollar modelos de optimización para minimizar los costos de transporte. El primero de estos modelos es el tema de este artículo.

En la sección 1, describiré en detalle y con ilustraciones el esquema para organizar la acción. Además, en la sección 2, la tarea de minimizar los costos de transporte se formalizará como la tarea de enrutar el problema de enrutamiento de vehículos de flota de vehículos heterogéneos con ventanas de tiempo. La Sección 3 está dedicada a resolver este problema usando un paquete distribuido libremente para resolver problemas de programación matemática lineal mixta entera GLPK.

1. La acción "Ardilla verde"

Desde 2014, el grupo de iniciativa Living Earth ha estado realizando una campaña mensual para separar la colección de Ardilla Verde reciclada en Novosibirsk. Al momento de escribir este artículo, se acepta el reciclaje con varias reservas de desechos plásticos etiquetados como PET, PE, PP, PS, vidrio, aluminio, hierro, electrodomésticos, papel de desecho y más. Más de 50 voluntarios participan en la preparación y realización de la acción. La acción no es comercial, su participación es gratuita y no implica una recompensa monetaria.

Puntos

La acción se lleva a cabo en 17 puntos de la ciudad, ubicados entre sí a distancias cubiertas por el automóvil en un período de 15 a 90 minutos. Uno de estos puntos en la foto: bolsas a la izquierda a lo largo de la pared para recoger varias fracciones de plástico, a la derecha, un camión, en el que todo está cargado en el futuro, y en el centro, un voluntario con orejas.



Toda la actividad en este punto está organizada por curadores que tienen restricciones en el momento en que están listos para cumplir con sus deberes. Al planificar una acción, los curadores informan el intervalo de tiempo dentro del cual la acción debe pasar en su punto.

También hay datos sobre los volúmenes promedio de reciclables recolectados en cada punto.

Rutas

Los puntos se organizan en rutas que son conducidas sucesivamente por un camión. Los movimientos de los camiones son monitoreados por supervisores de ruta que monitorean el entorno operativo y toman decisiones sobre el manejo de eventos especiales.



Camiones

Se alquilan de forma común en el marco de propuestas de alquiler por hora de vehículos de carga. No es posible compactar el plástico en su lugar, por lo tanto, el parámetro principal que caracteriza al camión es el volumen de la carrocería. La capacidad de carga en nuestro caso no es un factor limitante.

Los principales gastos de la acción están relacionados con el pago del alquiler de camiones, por lo tanto, su reducción es crítica para la existencia y el desarrollo de nuestra participación, que adquiere importancia institucional en el sentido de formar ideas sobre el consumo responsable. A continuación, se describirá un enfoque para resolver este problema, basado en la aplicación de métodos de optimización discretos, a saber, la programación matemática.

2. Formalización

Al construir el modelo matemático, nos mantendremos dentro del marco de los programas lineales de enteros mixtos, para los cuales es suficiente el conocimiento del álgebra de clase 7.

La única dificultad puede estar asociada con el uso de notación abstracta y signos de suma en las fórmulas. Espero que esto no asuste a los lectores que tienen encuentros poco frecuentes con textos matemáticos.

En el modelo de optimización, se pueden distinguir cuatro componentes:

• la formación de grupos de puntos que forman una ruta separada;
• definición de un esquema de desvío para cada uno de los grupos;
• cumplir con los requisitos para la hora de llegada del camión en cada punto;
• determinación del tipo de camión necesario para dar servicio a cada una de las rutas.

Consideramos cada una de las partes, introduciendo la notación necesaria según sea necesario.

Agrupación de puntos

Dejar $$$V = \ {1, \ puntos, n \}$ hay muchos índices de puntos de recolección de materiales reciclables, y el sitio donde se transportan los reciclables recolectados, lo llamaremos depósito , tiene un índice de 0. Poner $$$\ bar {V} = V \ cup \ {0 \}$

Cada grupo de puntos forma una ruta separada. A través de $$$R$ denotar el conjunto de números de ruta.

Deja la cantidad $$$z_ {ir}, i \ en I, r \ en R$ es igual a uno si el punto $$$i$ incluido en la ruta con el número $$$r$ , y cero en caso contrario. Entonces el requisito de que el punto $$$i \ en V$ debe ingresar una de las rutas puede escribirse como

$$

$$\ sum_ {r \ in R} z_ {ir} = z_ {i1} + z_ {i2} + \ dots + z_ {in} = 1.$$

Depot debe ingresar todas las rutas: $$$z_ {0r} = 1, r \ en R$


Definición de desvío

Las rutas son una secuencia alterna de puntos y cruces entre ellas. Formalmente, todos comienzan en uno de los puntos del set $$$V$ y terminar en el depósito, sin embargo, será más fácil suponer que todas las rutas son cíclicas. Esta suposición no cambia la esencia, pero hace que todos los vértices sean iguales: en este caso no hay vértices finales, todos son tránsito.

Por puntos $$$i, j \ in \ bar {V}$ y ruta $$$r \ en R$ configurar una variable $$$x_ {ijr}$ igual a uno si en la ruta con número $$$r$ camión moviéndose desde el punto $$$i$ hasta el punto $$$j$ , y cero en caso contrario.

Luego requerimos, en primer lugar, que el camión se mueva a lo largo de la ruta $$$r \ en R$ visitó el punto $$$i \ en V$ si ella, después de dividirse en grupos, cayó en el grupo con el número $$$r$ :

$$

$$\ sum_ {j \ in \ bar {V}} x_ {jir} = z_ {ir}, \ quad i \ in \ bar {V}, r \ in R.$$

En segundo lugar, el camión después de llegar al punto. $$$i \ in \ bar {V}$ debe dejarla.

$$

$$\ sum_ {j \ in \ bar {V}} x_ {jir} = \ sum_ {j \ in \ bar {V}} x_ {ijr}, \ quad i \ in \ bar {V}, r \ in R .$$

Puede notar que estas restricciones permiten las cantidades $$$x_ {ijr}$ Definir rutas que son un conjunto de bucles disjuntos. Rutas de este tipo, por supuesto, no tienen sentido, y se requieren varias restricciones para evitar esto.


Satisfacer los requisitos en el momento de la llegada del camión en cada punto

En otras palabras, debe visitar los puntos solo dentro de las ventanas de tiempo indicadas por los curadores. A través de $$$B_i$ y $$$E_i$ denotar, respectivamente, el comienzo y el final del intervalo de tiempo en el que el curador del punto $$$i$ Puede asistir.

Para rastrear la implementación de estas restricciones, necesitamos información sobre el tiempo que pasa el camión durante las paradas y cruces en la ruta. A través de $$$L_i, i \ en V$ denota la duración de la carga en el punto $$$i$ y a través de $$$D_ {ij}, i, j \ in \ bar {V}$ - tiempo de moverse desde un punto $$$i$ hasta el punto $$$j$ Hacemos una reserva que $$$D_ {0i} = 0$ para todos $$$i \ in \ bar {V}$ y generalmente se puede realizar $$$D_ {ij} \ neq D_ {ji}$ para cualquier $$$i \ neq j$

Introducimos variables no negativas $$$a_i, i \ in \ bar {V}$ y $$$w_ {ir}, i \ in \ bar {V}, r \ in R$ igual a los tiempos de llegada y de espera en el punto $$$i$ al conducir por una ruta $$$r$ , respectivamente. Para los valores ingresados, se deben cumplir las siguientes relaciones.

El tiempo de espera no puede ser inferior al tiempo requerido para cargar

$$

$$w_ {ir} \ geq L_iz_ {ir}, \ quad i \ in \ bar {V}, r \ in R,$$

e igual a cero si el punto no pertenece a la ruta $$$r$

$$

$$w_ {ir} \ leq Mz_ {ir}, \ quad i \ in \ bar {V}, r \ in R,$$

Hora de llegada al punto $$$j$ calculado en los momentos apropiados para el punto anterior $$$i$ Aquí hay una constante bastante grande $$$M$ Se utiliza para eliminar dependencias innecesarias al moverse entre $$$i$ y $$$j$ no hecho

$$

$$a_i + \ sum_ {r \ in R} w_ {ir} + D_ {ij} \ leq a_j + M (1 - \ sum_ {r \ in R} x_ {ijr}), \ quad i \ in I, j \ en V,$$

La llegada y salida del camión debe estar dentro del intervalo indicado por el curador.

$$

$$a_i \ geq B_i, \ quad i \ en V,$$

$$

$$a_i + \ sum_ {r \ in R} w_ {ir} \ leq E_i, \ quad i \ in V.$$

Determinar el tipo de camión necesario para dar servicio a cada ruta
Denota los muchos tipos de camiones disponibles para alquilar por $$$T$ Tipo de camión $$$t \ en T$ caracterizado por el volumen corporal $$$C_t$ y el costo de una hora de alquiler $$$P_t$ Tiempo mínimo de alquiler de camiones $$$t$ denotar por $$$U_t ^ 0$ La cantidad de reciclables recogidos en el punto $$$i \ en V$ denotar por $$$G_i$

Introducimos variables $$$y_ {tr}, t \ en T, r \ en R$ igual a uno si el tipo de camión $$$t$ asignado a la ruta de servicio con número $$$r$ , y cero en caso contrario.

Variables enteras $$$u_ {tr}, t \ en T, r \ en R$ establecer el momento de alquilar un tipo de camión $$$t$ sirviendo la ruta con número $$$r$
Para cada ruta, $$$r \ en R$ , debe asignar el tipo de camión:

$$

$$\ sum_ {t \ en T} y_ {tr} = 1, \ quad r \ en R$$

De acuerdo con el desglose de puntos entre rutas, algunas rutas pueden resultar triviales, es decir, contener solo depósitos. Si la ruta $$$r$ no trivial, entonces el camión asignado se alquila al menos $$$U_t ^ 0$ horas

$$

$$u_ {tr} \ geq U_t ^ 0 (y_ {tr} - \ sum_ {i \ en V} z_ {ir}), \ quad t \ en T, r \ en R.$$

Al mismo tiempo, la duración del contrato de arrendamiento también debe exceder la duración total de estacionamiento y movimiento a lo largo de la ruta.

$$

$$u_ {tr} \ geq \ sum_ {i \ in V} \ sum_ {j \ in \ bar {V}} D_ {ij} x_ {ijr} + \ sum_ {i \ in \ bar {V}} w_ { ir} -M (1-y_ {tr}), \ quad r \ en R, t \ en T.$$

Agregue restricciones al proporcionar la propiedad: si el camión es de tipo $$$t$ no asignado a una ruta $$$r$ , su tiempo de alquiler es cero.

$$

$$u_ {tr} \ leq My_ {tr}.$$

Todos los reciclables recogidos en los puntos de ruta deben caber en la parte trasera del camión.

$$

$$\ sum_ {i \ en V} G_iz_ {ir} \ leq \ sum_ {t \ en T} C_ty_ {tr}, \ quad r \ en R.$$

Finalmente, nuestro objetivo es minimizar el costo de alquilar camiones, que, utilizando las designaciones introducidas, se escribe como $$$\ sum_ {t \ in T} \ sum_ {r \ in R} P_tu_ {tr}$

Busca una solución

Es fácil verificar que todas las expresiones involucradas en el modelo de optimización son funciones lineales de variables, por lo tanto, para encontrar las soluciones exactas y aproximadas, puede usar paquetes estándar para resolver problemas de programación de enteros mixtos como Gurobi , CPLEX , Xpress , ORtools , SCIP , BLIS , etc.
Escribimos un modelo para minimizar los costos de transporte en el lenguaje GMPL. Esto nos permitirá usar el paquete GLPK gratuito para nuestros propósitos. Para escribir código y depurar el modelo, será conveniente descargar el entorno de desarrollo GUSEK , que ya contiene GLPK en su composición.

GUSEK se ve así:



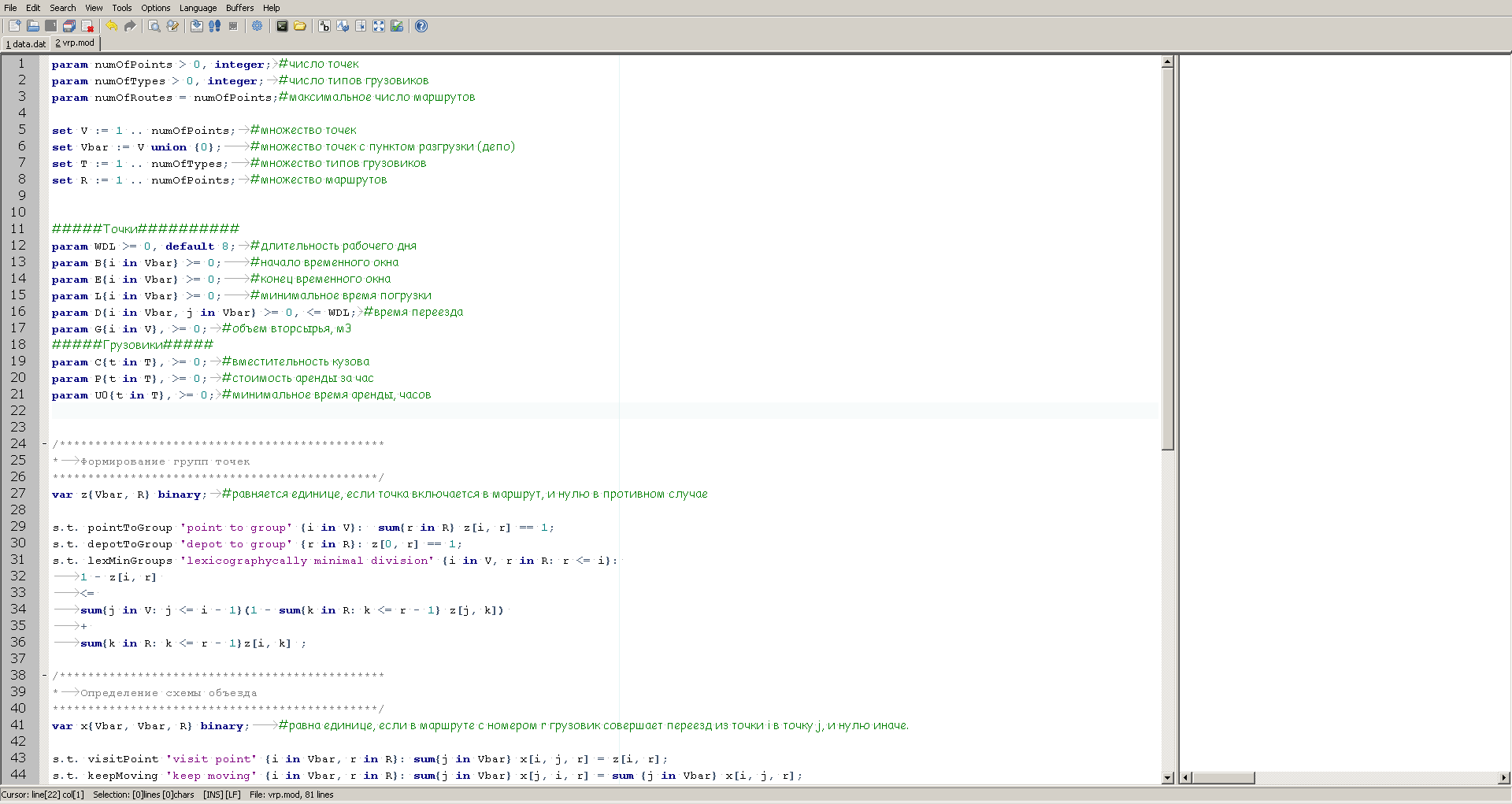
A la izquierda vemos una descripción del modelo, y a la derecha hay una ventana para mostrar información sobre el progreso del cálculo, que el solucionador proporcionará después del lanzamiento.


Para comenzar rápidamente, también agregaré datos tomados de mi cabeza preparados para su uso en el modelo:


Después de copiar el código del modelo en un archivo con el nombre, por ejemplo, model.mod, y los datos de entrada al archivo data.dat, todo está listo para ejecutarse. Establecemos un límite en el tiempo de cálculo de 100 segundos (esto se hace usando la tecla --tmlim [tiempo en segundos]), transferimos la ruta al archivo con los datos de entrada (usando la tecla -d [ruta del archivo]),



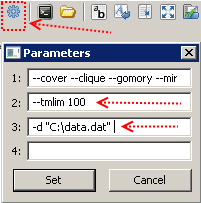
y presione F5. Si tiene éxito, aparecerán mensajes en la ventana de la derecha, y después de cien segundos tendremos la mejor solución que GLPK logró encontrar en el tiempo asignado.



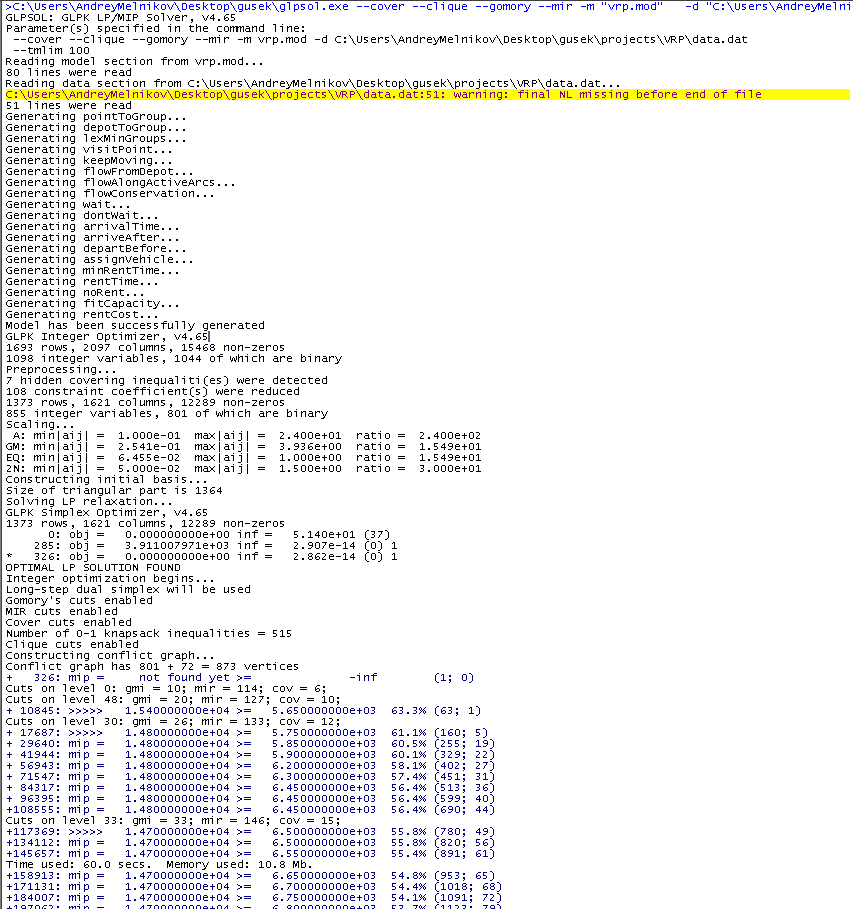
En el texto azul, nos interesa el significado después de la inscripción "mip =". Como puede ver, disminuye de vez en cuando. Todas las nuevas soluciones están en proceso de trabajo, el valor de los costos de transporte en el mejor de los casos se muestra en esta columna (hay 14700 hasta ahora). El siguiente número es el límite inferior para la mejor solución existente, es decir, óptima . Inicialmente, la estimación se subestima significativamente, pero se refina con el tiempo, es decir, aumenta. Los valores a la izquierda y a la derecha son convergentes, y la brecha relativa entre ellos en el momento de la captura de pantalla es del 54,1%. Tan pronto como este número sea cero, el algoritmo demostrará que la mejor solución encontrada es la mejor posible. No siempre se justifica esperar este evento en la práctica, y no solo porque es mucho tiempo, sino que es importante hacer una reserva de que, por regla general, una buena solución es relativamente rápida, y los costos de tiempo principales están asociados con el refinamiento de la estimación requerida para probar lo mejor posible.

En lugar de una conclusión

Los problemas de enrutamiento son extremadamente complejos desde el punto de vista informático, y con el aumento en el número de puntos que deben visitarse, el tiempo requerido para que un solucionador encuentre una solución y demuestre que su optimización está creciendo rápidamente. Sin embargo, para ejemplos bastante pequeños, en un período de tiempo razonable, el solucionador puede construir un conjunto exitoso de rutas y puede usarse para apoyar la toma de decisiones. El análisis de las opciones de enrutamiento propuestas por el modelo nos ayudó a descubrir oportunidades significativas para la reducción de costos, y esto es crítico para la existencia y el desarrollo del stock.

Nuestros esfuerzos adicionales se dirigieron al trabajo con incertidumbre en los volúmenes de reciclables recogidos en los puntos. Estamos desarrollando una serie de modelos de programación estocástica para tomar decisiones estratégicas y operativas en el enrutamiento de camiones. Si el tema resulta relevante y despierta interés, escribiré sobre esto también, porque pronto todos tendremos que profundizar más en la resolución de problemas ambientales, que es en lo que deseo que tengamos éxito.