Redes neuronales y aprendizaje profundo, capítulo 1: uso de redes neuronales para reconocer números escritos a mano

Nota

Aquí hay una traducción del libro en línea gratuito de Michael Nielsen, Neural Networks and Deep Learning, distribuido bajo la Licencia Creative Commons Reconocimiento-No Comercial 3.0 Unported . La motivación para su creación fue la experiencia exitosa de traducir un libro de texto de programación, Expressive JavaScript . El libro sobre redes neuronales también es bastante popular; los autores de artículos en inglés lo citan activamente. No encontré sus traducciones, excepto la traducción del comienzo del primer capítulo con abreviaturas .

Aquellos que quieran agradecer al autor del libro pueden hacerlo en su página oficial , mediante transferencia a través de PayPal o Bitcoin. Para apoyar al traductor en Habré hay un formulario "para apoyar al autor".

Introduccion

Este tutorial le informará en detalle sobre conceptos como:

• Redes neuronales: un excelente paradigma de software, creado bajo la influencia de la biología, y que permite que la computadora aprenda basándose en observaciones.
• El aprendizaje profundo es un poderoso conjunto de técnicas de entrenamiento de redes neuronales.

Las redes neuronales (NS) y el aprendizaje profundo (GO) brindan hoy la mejor solución a muchos problemas en las áreas de reconocimiento de imágenes, procesamiento de voz y lenguaje natural. Este tutorial le enseñará muchos de los conceptos clave que sustentan NS y GO.

¿De qué trata este libro?

NS es uno de los mejores paradigmas de software jamás inventado por el hombre. Con un enfoque de programación estándar, le decimos a la computadora qué hacer, dividir las tareas grandes en muchas pequeñas y determinar con precisión las tareas que la computadora realizará fácilmente. En el caso de la Asamblea Nacional, por el contrario, no le decimos a la computadora cómo resolver el problema. Él mismo aprende esto sobre la base de "observaciones" de los datos, "inventando" su propia solución al problema.

El aprendizaje automatizado basado en datos suena prometedor. Sin embargo, hasta 2006, no sabíamos cómo capacitar a la Asamblea Nacional para que pudieran trascender los enfoques más tradicionales, con la excepción de algunos casos especiales. En 2006, técnicas de entrenamiento de los llamados redes neuronales profundas (GNS). Ahora estas técnicas se conocen como aprendizaje profundo (GO). Continuaron desarrollándose, y hoy GNS y GO han logrado resultados sorprendentes en muchas tareas importantes relacionadas con la visión por computadora, el reconocimiento del habla y el procesamiento del lenguaje natural. A gran escala, están siendo implementados por empresas como Google, Microsoft y Facebook.

El propósito de este libro es ayudarlo a dominar los conceptos clave de las redes neuronales, incluidas las técnicas modernas de GO. Después de trabajar con el tutorial, escribirá un código que usa NS y GO para resolver problemas complejos de reconocimiento de patrones. Tendrá una base para usar NS y defensa civil en el enfoque para resolver sus propios problemas.

Enfoque basado en principios

Una de las creencias subyacentes en el libro es que es mejor adquirir una comprensión sólida de los principios clave de la Asamblea Nacional y la Sociedad Civil que obtener conocimiento de una larga lista de ideas diferentes. Si comprende bien las ideas clave, comprenderá rápidamente otro material nuevo. En el lenguaje del programador, podemos decir que estudiaremos la sintaxis básica, las bibliotecas y las estructuras de datos del nuevo lenguaje. Es posible que reconozca solo una pequeña fracción de todo el idioma (muchos idiomas tienen bibliotecas estándar inmensas), sin embargo, puede comprender nuevas bibliotecas y estructuras de datos de forma rápida y sencilla.

Entonces, este libro categóricamente no es material educativo sobre cómo usar una biblioteca en particular para la Asamblea Nacional. Si solo quieres aprender a trabajar con la biblioteca, ¡no leas el libro! Encuentre la biblioteca que necesita y trabaje con materiales de capacitación y documentación. Pero tenga en cuenta: aunque este enfoque tiene la ventaja de resolver el problema instantáneamente, si desea comprender exactamente qué está sucediendo dentro de la Asamblea Nacional, si desea dominar ideas que serán relevantes en muchos años, entonces no será suficiente para que simplemente estudie algún tipo de biblioteca de moda Debe comprender las ideas confiables y a largo plazo que subyacen en el trabajo de la Asamblea Nacional. La tecnología va y viene, y las ideas duran para siempre.

Enfoque práctico

Estudiaremos los principios básicos con el ejemplo de una tarea específica: enseñar a una computadora a reconocer números escritos a mano. Utilizando enfoques de programación tradicionales, esta tarea es extremadamente difícil de resolver. Sin embargo, podemos resolverlo bastante bien con un NS simple y varias docenas de líneas de código, sin bibliotecas especiales. Además, mejoraremos gradualmente este programa, incluyendo constantemente más y más ideas clave sobre la Asamblea Nacional y la Defensa Civil.

Este enfoque práctico significa que necesitará algo de experiencia en programación. Pero no tienes que ser un programador profesional. Escribí el código de Python (versión 2.7) que debería quedar claro incluso si no ha escrito programas de Python. En el proceso de estudio, crearemos nuestra propia biblioteca para la Asamblea Nacional, que puede utilizar para experimentos y capacitación adicional. Todo el código se puede descargar aquí . Una vez terminado el libro, o en el proceso de lectura, puede elegir una de las bibliotecas más completas para la Asamblea Nacional, adaptada para su uso en estos proyectos.

Los requisitos matemáticos para comprender el material son bastante promedio. La mayoría de los capítulos tienen partes matemáticas, pero generalmente son álgebra elemental y gráficos de funciones. A veces uso matemáticas más avanzadas, pero estructuré el material para que puedas entenderlo, incluso si algunos detalles te eluden. La mayoría de las matemáticas se usan en el capítulo 2, que requiere un poco de matanálisis y álgebra lineal. Para aquellos a quienes no están familiarizados, comienzo el Capítulo 2 con una introducción a las matemáticas. Si le resulta difícil, simplemente omita el capítulo hasta el informe. En cualquier caso, no te preocupes por esto.

Un libro rara vez se orienta al mismo tiempo hacia una comprensión de los principios y un enfoque práctico. Pero creo que es mejor estudiar sobre la base de las ideas fundamentales de la Asamblea Nacional. Escribiremos código de trabajo, y no solo estudiaremos teoría abstracta, y usted puede explorar y extender este código. De esta manera, comprenderá los conceptos básicos, tanto la teoría como la práctica, y podrá aprender más.

Ejercicios y tareas

Los autores de libros técnicos a menudo advierten al lector que simplemente necesita completar todos los ejercicios y resolver todos los problemas. Al leerme tales advertencias, siempre me parecen un poco extrañas. ¿Me pasará algo malo si no realizo ejercicios y resuelvo problemas? No por supuesto. Ahorraré tiempo con una comprensión menos profunda. A veces vale la pena. A veces no.

¿Qué vale la pena hacer con este libro? Le aconsejo que intente completar la mayoría de los ejercicios, pero no intente resolver la mayoría de las tareas.

La mayoría de los ejercicios deben completarse porque estos son controles básicos para una comprensión adecuada del material. Si no puede realizar el ejercicio con relativa facilidad, debe haberse perdido algo fundamental. Por supuesto, si realmente está atascado en algún tipo de ejercicio, suéltelo, tal vez sea una especie de pequeño malentendido, o tal vez haya formulado algo mal. Pero si la mayoría de los ejercicios le causan dificultades, lo más probable es que necesite volver a leer el material anterior.

Las tareas son otra cosa. Son más difíciles que los ejercicios, y con algunos tendrás dificultades. Esto es molesto, pero, por supuesto, la paciencia frente a tal decepción es la única forma de comprender y absorber realmente el tema.

Por lo tanto, no recomiendo resolver todos los problemas. Mejor aún: elige tu propio proyecto. Es posible que desee utilizar NS para clasificar su colección de música. O para predecir el valor de las acciones. O algo mas. Pero encuentra un proyecto interesante para ti. Y luego puede ignorar las tareas del libro, o utilizarlas simplemente como inspiración para trabajar en su proyecto. Los problemas con su propio proyecto le enseñarán más que trabajar con cualquier cantidad de tareas. La participación emocional es un factor clave en el logro del dominio.

Por supuesto, si bien es posible que no tenga un proyecto de este tipo. Esto es normal Resuelve tareas para las que sientas una motivación intrínseca. Use material del libro para ayudarlo a encontrar ideas para proyectos creativos personales.

Capitulo 1

El sistema visual humano es una de las maravillas del mundo. Considere la siguiente secuencia de números escritos a mano:



La mayoría de la gente los leerá fácilmente, como 504192. Pero esta simplicidad es engañosa. En cada hemisferio del cerebro, una persona tiene una corteza visual primaria , también conocida como V1, que contiene 140 millones de neuronas y decenas de miles de millones de conexiones entre ellas. Al mismo tiempo, no solo V1 está involucrado en la visión humana, sino toda una secuencia de regiones cerebrales (V2, V3, V4 y V5) que se dedican al procesamiento de imágenes cada vez más complejo. Llevamos en nuestras cabezas una supercomputadora sintonizada por la evolución durante cientos de millones de años, y perfectamente adaptada para comprender el mundo visible. Reconocer números escritos a mano no es tan fácil. Es solo que nosotros, las personas, sorprendentemente, sorprendentemente bien, reconocemos lo que nuestros ojos nos muestran. Pero casi todo este trabajo se lleva a cabo inconscientemente. Y, por lo general, no le damos importancia a la difícil tarea que resuelven nuestros sistemas visuales.

La dificultad de reconocer patrones visuales se hace evidente cuando intentas escribir un programa de computadora para reconocer números como los anteriores. Lo que parece fácil en nuestra ejecución de repente resulta ser extremadamente complejo. El simple concepto de cómo reconocemos las formas ("el nueve tiene un bucle en la parte superior y la barra vertical en la parte inferior derecha") no es tan simple para una expresión algorítmica. Al tratar de articular estas reglas con claridad, rápidamente queda atrapado en un atolladero de excepciones, dificultades y ocasiones especiales. La tarea parece desesperada.

Enfoque NS para resolver el problema de una manera diferente. La idea es tomar los muchos números escritos a mano conocidos como ejemplos de enseñanza,



y desarrolle un sistema que pueda aprender de estos ejemplos. En otras palabras, la Asamblea Nacional usa ejemplos para construir automáticamente reglas de reconocimiento de dígitos escritas a mano. Además, al aumentar el número de ejemplos de capacitación, la red puede aprender más sobre números escritos a mano y mejorar su precisión. Entonces, aunque he citado más de 100 estudios de casos, quizás podamos crear un mejor sistema de reconocimiento de escritura a mano utilizando miles o incluso millones y miles de millones de estudios de casos.

En este capítulo, escribiremos un programa de computadora que implementa el aprendizaje NS para reconocer números escritos a mano. El programa tendrá solo 74 líneas y no utilizará bibliotecas especiales para la Asamblea Nacional. Sin embargo, este breve programa podrá reconocer números escritos a mano con una precisión de más del 96%, sin necesidad de intervención humana. Además, en futuros capítulos desarrollaremos ideas que pueden mejorar la precisión al 99% o más. De hecho, los mejores NS comerciales hacen un trabajo tan bueno que los bancos los utilizan para procesar cheques y el servicio postal para reconocer direcciones.

Nos concentramos en el reconocimiento de escritura a mano, ya que este es un gran prototipo de una tarea para estudiar NS. Tal prototipo es ideal para nosotros: es una tarea difícil (reconocer números escritos a mano no es una tarea fácil), pero no tan complicada que requiere una solución extremadamente compleja o una inmensa potencia informática. Además, esta es una excelente manera de desarrollar técnicas más complejas, como GO. Por lo tanto, en el libro volveremos constantemente a la tarea de reconocimiento de escritura a mano. Más adelante discutiremos cómo se pueden aplicar estas ideas a otras tareas de la visión por computadora, al reconocimiento de voz, el procesamiento del lenguaje natural y otras áreas.

Por supuesto, si el propósito de este capítulo fuera solo escribir un programa para reconocer números escritos a mano, ¡entonces el capítulo sería mucho más corto! Sin embargo, en el proceso desarrollaremos muchas ideas clave relacionadas con NS, incluidos dos tipos importantes de neuronas artificiales ( perceptrón y neurona sigmoidea), y el algoritmo de aprendizaje estándar de NS, el descenso de gradiente estocástico . En el texto, me concentro en explicar por qué todo se hace de esta manera, y en dar forma a su comprensión de la Asamblea Nacional. Esto requiere una conversación más larga que si acabara de presentar la mecánica básica de lo que está sucediendo, pero cuesta una comprensión más profunda que tendrá. Entre otras ventajas: al final del capítulo comprenderá qué es una defensa civil y por qué es tan importante.

Perceptrones

¿Qué es una red neuronal? Para comenzar, hablaré sobre un tipo de neurona artificial llamada perceptrón. Los perceptrones fueron inventados por el científico Frank Rosenblatt en los años 50 y 60, inspirados en los primeros trabajos de Warren McCallock y Walter Pitts . Hoy en día, otros modelos de neuronas artificiales se usan con mayor frecuencia: en este libro, y los trabajos más modernos sobre NS utilizan principalmente el modelo sigmoide de la neurona. La veremos pronto. Pero para comprender por qué las neuronas sigmoideas se definen de esta manera, vale la pena pasar tiempo analizando el perceptrón.

Entonces, ¿cómo funcionan los perceptrones? El perceptrón recibe varios números binarios x ₁ , x ₂ , ... y da un número binario:



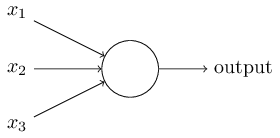
En este ejemplo, el perceptrón tiene tres números de entrada, x ₁ , x ₂ , x ₃ . En general, puede haber más o menos de ellos. Rosenblatt propuso una regla simple para calcular el resultado. Introdujo pesos, w ₁ , w ₂ , números reales, expresando la importancia de los números de entrada correspondientes para los resultados. La salida de una neurona, 0 o 1, está determinada por si una suma ponderada es menor o mayor que cierto umbral [umbral] $$$\ sum_j w_jx_j$ . Al igual que los pesos, el umbral es un número real, un parámetro de una neurona. En términos matemáticos:

$$

$$salida = \ begin {cases} 0 ~ if ~ \ sum_j w_jx_j \ leq umbral \\ 1 ~ if ~ \ sum_j w_jx_j> umbral \ end {casos} \ tag {1}$$

¡Esa es toda la descripción del perceptrón!

Este es el modelo matemático básico. Un perceptrón puede considerarse como un tomador de decisiones al sopesar la evidencia. Déjame darte un ejemplo no muy realista, pero simple. Digamos que se acerca el fin de semana, y escuchaste que se celebrará un festival de queso en tu ciudad. Te gusta el queso y trata de decidir si ir al festival o no. Puede tomar una decisión sopesando tres factores:

1. ¿Hace buen tiempo?
2. ¿Tu pareja quiere ir contigo?
3. ¿Está el festival lejos del transporte público? (No tienes coche).

Estos tres factores pueden representarse como variables binarias x ₁ , x ₂ , x ₃ . Por ejemplo, x ₁ = 1 si el clima es bueno y 0 si es malo. x ₂ = 1 si tu compañero quiere ir, y 0 si no. Lo mismo para x ₃ .

Ahora, digamos que eres tan fanático del queso que estás listo para ir al festival, incluso si a tu pareja no le interesa y es difícil llegar a él. Pero quizás odies el mal tiempo y, en caso de mal tiempo, no irás al festival. Puede usar perceptrones para modelar tal proceso de toma de decisiones. Una forma es elegir el peso w ₁ = 6 para el clima, y ​​w ₂ = 2, w ₃ = 2 para otras condiciones. Un valor mayor de w ₁ significa que el clima le importa mucho más que si su pareja se unirá a usted o la proximidad del festival a una parada. Finalmente, suponga que selecciona el umbral 5 para el perceptrón. Con estas opciones, el perceptrón implementa el modelo de decisión deseado, dando 1 cuando el clima es bueno y 0 cuando es malo. El deseo del compañero y la proximidad de la parada no afectan el valor de salida.

Al cambiar los pesos y los umbrales, podemos obtener diferentes modelos de toma de decisiones. Por ejemplo, supongamos que tomamos el umbral 3. Luego, el perceptrón decide que debe ir al festival, ya sea cuando hace buen tiempo o cuando el festival está cerca de una parada de autobús y su pareja acepta ir con usted. En otras palabras, el modelo es diferente. Bajar el umbral significa que quieres ir más al festival.

¡Obviamente, el perceptrón no es un modelo humano completo de toma de decisiones! Pero este ejemplo muestra cómo un perceptrón puede pesar diferentes tipos de evidencia para tomar decisiones. Parece posible que una red compleja de perceptrones pueda tomar decisiones muy complejas:



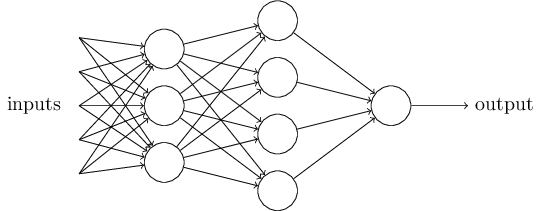
En esta red, la primera columna de perceptrones, lo que llamamos la primera capa de perceptrones, toma tres decisiones muy simples, sopesando la evidencia de entrada. ¿Qué pasa con los perceptrones de la segunda capa? Cada uno de ellos toma una decisión, sopesando los resultados de la primera capa de toma de decisiones. De esta manera, el perceptrón de la segunda capa puede tomar una decisión a un nivel más complejo y abstracto en comparación con el perceptrón de la primera capa. E incluso los perceptrones en la tercera capa pueden tomar decisiones aún más complejas.De esta manera, una red multicapa de perceptrones puede manejar decisiones complejas.

Por cierto, cuando determiné el perceptrón, dije que solo tiene un valor de salida. Pero en la red en la parte superior, los perceptrones parecen tener varios valores de salida. De hecho, solo tienen una salida. Muchas flechas de salida son solo una forma conveniente de mostrar que la salida del perceptrón se usa como entrada de varios otros perceptrones. Esto es menos engorroso que dibujar una única salida de ramificación.

Simplifiquemos la descripción de los perceptrones. Condición$$Σ j de w j x j > t r un e s h o l d incómoda, y podemos estar de acuerdo en dos cambios para la grabación de su simplicidad. Lo primero es grabar$\sum_j w_jx_j > treshold$$$Σ j de w j x j como el producto escalar,$\sum_j w_jx_j$$$w ⋅ x = ∑ j w j x j , donde w y x son vectores cuyos componentes son pesos y datos de entrada, respectivamente. El segundo es transferir el umbral a otra parte de la desigualdad y reemplazarlo con un valor conocido como desplazamiento de perceptrón [sesgo],$w \cdot x = \sum_j w_jx_j$$$$b \equiv −threshold$ . Usando el desplazamiento en lugar de un umbral, podemos reescribir la regla del perceptrón:

$$

$$output = \begin{cases} 0 ~ if ~ w \cdot x + b \leq 0 \\ 1 ~ if ~ w \cdot x + b > 0 \end{cases} \tag{2}$$

El desplazamiento se puede representar como una medida de lo fácil que es obtener un valor de 1 en la salida del perceptrón. O, en términos biológicos, el desplazamiento es una medida de lo fácil que es activar el perceptrón. Un perceptrón con un sesgo muy grande es extremadamente fácil de dar 1. Pero con un sesgo negativo muy grande, esto es difícil de hacer. Obviamente, la introducción del sesgo es un pequeño cambio en la descripción de los perceptrones, pero luego veremos que conduce a una mayor simplificación de la grabación. Por lo tanto, además no usaremos el umbral, sino que siempre usaremos el desplazamiento.

Describí los perceptrones en términos del método de sopesar la evidencia para la toma de decisiones. Otro método de uso es el cálculo de funciones lógicas elementales, que generalmente consideramos los cálculos principales, como AND, OR y NAND. Supongamos, por ejemplo, que tenemos un perceptrón con dos entradas, el peso de cada una de ellas es -2, y su desplazamiento es 3. Aquí está: la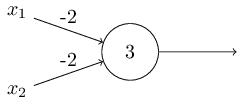



entrada 00 da la salida 1, porque (−2) ∗ 0 + (- 2 ) ∗ 0 + 3 = 3 es mayor que cero. Los mismos cálculos dicen que las entradas 01 y 10 dan 1. Pero 11 en la entrada da 0 en la salida, ya que (−2) ∗ 1 + (- 2) ∗ 1 + 3 = −1, menor que cero. ¡Por lo tanto, nuestro perceptrón implementa la función NAND!

Este ejemplo muestra que los perceptrones se pueden usar para calcular funciones lógicas básicas. De hecho, podemos usar redes perceptron para calcular cualquier función lógica en general. El hecho es que la compuerta lógica NAND es universal para los cálculos: es posible construir cualquier cálculo sobre la base. Por ejemplo, puede usar puertas NAND para crear un circuito que agregue dos bits, x ₁ y x ₂ . Para hacer esto, calcule la suma de bits$$x 1 ⊕ x 2 , así comola bandera de acarreo, que es 1 cuando x₁y x₂son 1, es decir, la bandera de acarreo es simplemente el resultado de la multiplicación por bits x₁x₂:para obtener la red equivalente de los perceptrones, reemplazamos todos Las compuertas NAND son perceptrones con dos entradas, el peso de cada una de ellas es -2, y con un desplazamiento de 3. Aquí está la red resultante. 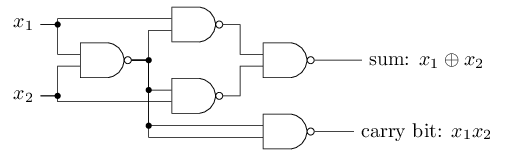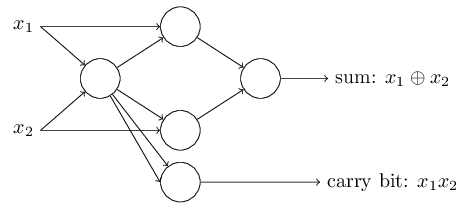Tenga en cuenta que moví el perceptrón correspondiente a la válvula inferior derecha, solo para que sea más conveniente dibujar flechas:$x_1 \oplus x_2$







Un aspecto notable de esta red perceptrón es que la salida de la izquierda se usa dos veces como entrada en la parte inferior. Al definir el modelo del perceptrón, no mencioné la admisibilidad de tal esquema de doble salida en el mismo lugar. De hecho, en realidad no importa. Si no queremos permitir esto, simplemente podemos combinar dos líneas con pesos de -2 en una con un peso de -4. (Si esto no te parece obvio, detente y demuéstralo a ti mismo). Después de este cambio, la red se ve de la siguiente manera, con todos los pesos no asignados iguales a -2, todos los desplazamientos iguales a 3, y se marca un peso -4:



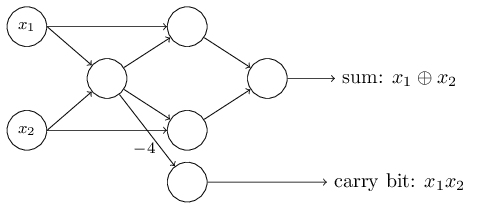Tal registro de perceptrones que tienen una salida pero no entradas:



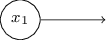Es solo una abreviatura. Esto no significa que no tenga entradas. Para entender esto, supongamos que tenemos un perceptrón sin entradas. Entonces la suma ponderada ∑ _j w _j x _j siempre sería cero, por lo que el perceptrón daría 1 para b> 0 y 0 para b ≤ 0. Es decir, el perceptrón solo daría un valor fijo, y no lo que necesitamos (x ₁ en el ejemplo arriba). Es mejor considerar los perceptrones de entrada no como perceptrones, sino como unidades especiales que simplemente se definen para producir los valores deseados x ₁ , x ₂ , ...

El ejemplo del sumador demuestra cómo se puede utilizar una red perceptrón para simular un circuito que contiene muchas compuertas NAND. Y dado que estas puertas son universales para los cálculos, por lo tanto, los perceptrones son universales para los cálculos.

La versatilidad computacional de los perceptrones es alentadora y decepcionante. Es alentador, asegurando que la red perceptron pueda ser tan poderosa como cualquier otro dispositivo informático. Decepcionante, dando la impresión de que los perceptrones son solo un nuevo tipo de puerta lógica NAND. Más o menos descubrimiento!

Sin embargo, la situación es realmente mejor. Resulta que podemos desarrollar algoritmos de entrenamiento que pueden ajustar automáticamente los pesos y los desplazamientos de la red de las neuronas artificiales. Este ajuste tiene lugar en respuesta a estímulos externos, sin la intervención directa de un programador. Estos algoritmos de aprendizaje nos permiten usar neuronas artificiales de una manera radicalmente diferente de las puertas lógicas ordinarias. En lugar de registrar explícitamente un circuito desde puertas NAND y otras, nuestras redes neuronales simplemente pueden aprender a resolver problemas, a veces aquellos para los que sería extremadamente difícil diseñar directamente un circuito regular.

Neuronas sigmoideas

Los algoritmos de aprendizaje son geniales. Sin embargo, ¿cómo desarrollar un algoritmo para una red neuronal? Supongamos que tenemos una red de perceptrones que queremos usar para capacitarnos en la resolución de un problema. Suponga que la entrada a la red puede ser píxeles de una imagen escaneada de un dígito escrito a mano. Y queremos que la red conozca los pesos y las compensaciones necesarias para clasificar correctamente los números. Para comprender cómo puede funcionar dicha capacitación, imaginemos que estamos cambiando ligeramente un cierto peso (o sesgo) en la red. Queremos que este pequeño cambio conduzca a un pequeño cambio en la salida de la red. Como veremos pronto, esta propiedad hace posible el aprendizaje. Esquemáticamente, queremos lo siguiente (obviamente, ¡tal red es demasiado simple para reconocer la escritura a mano!):



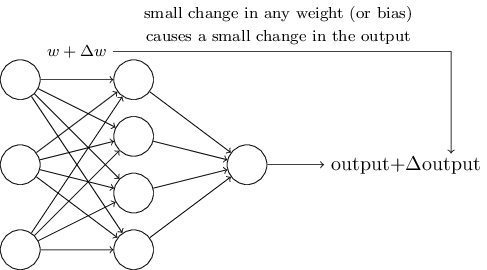
Si un pequeño cambio en el peso (o sesgo) llevara a un pequeño cambio en el resultado de salida, podríamos cambiar los pesos y los sesgos para que nuestra red se comporte un poco más cerca de lo que queremos. Por ejemplo, supongamos que la red asignó incorrectamente la imagen a "8", aunque debería haber sido a "9". Podríamos descubrir cómo hacer un pequeño cambio en el peso y el desplazamiento para que la red se acerque un poco más a clasificar la imagen como "9". Y luego repetiríamos esto, cambiando pesos y turnos una y otra vez para obtener el mejor y el mejor resultado. La red aprendería.

El problema es que si hay perceptrones en la red, esto no sucede. Un pequeño cambio en los pesos o el desplazamiento de cualquier perceptrón a veces puede conducir a un cambio en su salida al opuesto, por ejemplo, de 0 a 1. Tal cambio puede cambiar el comportamiento del resto de la red de una manera muy complicada. E incluso si ahora nuestro "9" se reconoce correctamente, el comportamiento de la red con todas las otras imágenes probablemente ha cambiado por completo de una manera que es difícil de controlar. Debido a esto, es difícil imaginar cómo podemos ajustar gradualmente los pesos y las compensaciones para que la red se acerque gradualmente al comportamiento deseado. Quizás hay alguna forma inteligente de solucionar este problema. Pero no existe una solución simple al problema de aprender una red de perceptrones.

Este problema se puede evitar introduciendo un nuevo tipo de neurona artificial llamada neurona sigmoidea. Son similares a los perceptrones, pero modificados para que los pequeños cambios en los pesos y las compensaciones den como resultado solo pequeños cambios en la salida. Este es un hecho básico que permitirá que la red de neuronas sigmoides aprenda.

Déjame describir una neurona sigmoidea. Los dibujaremos de la misma manera que los perceptrones:



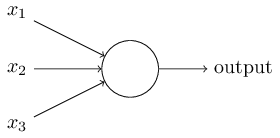
Tiene la misma entrada x ₁ , x ₂ , ... Pero en lugar de ser igual a 0 o 1, estas entradas pueden tener cualquier valor en el rango de 0 a 1. Por ejemplo, un valor de 0.638 será una entrada válida para neurona sigmoidea (CH). Al igual que el perceptrón, SN tiene pesos para cada entrada, w ₁ , w ₂ , ... y el sesgo total b. Pero su valor de salida no será 0 o 1. Será σ (w⋅x + b), donde σ es el sigmoide.

Por cierto, σ a veces se llama una función logística , y esta clase de neuronas se llama neuronas logísticas. Es útil recordar esta terminología, ya que estos términos son utilizados por muchas personas que trabajan con redes neuronales. Sin embargo, nos adheriremos a la terminología sigmoidea.

La función se define de la siguiente manera:

$$

$$\ sigma (z) \ equiv \ frac {1} {1 + e ^ {- z}} \ tag {3}$$

En nuestro caso, el valor de salida de la neurona sigmoidea con datos de entrada x ₁ , x ₂ , ... por los pesos w ₁ , w ₂ , ... y el desplazamiento b se considerará como:

$$

$$\ frac {1} {1 + exp (- \ sum_j w_jx_j - b)} \ tag {4}$$

A primera vista, CH parece completamente diferente a las neuronas. El aspecto algebraico de un sigmoide puede parecer confuso y oscuro si no está familiarizado con él. De hecho, hay muchas similitudes entre los perceptrones y el SN, y la forma algebraica de un sigmoide resulta ser más un detalle técnico que una barrera seria para la comprensión.

Para comprender las similitudes con el modelo de perceptrón, suponga que z ≡ w ⋅ x + b es un número positivo grande. Entonces e - z ≈ 0, por lo tanto, σ (z) ≈ 1. En otras palabras, cuando z = w ⋅ x + b es grande y positivo, el rendimiento de SN es aproximadamente igual a 1, como para el perceptrón. Suponga que z = w ⋅ x + b es grande con un signo menos. Entonces e - z → ∞, y σ (z) ≈ 0. Entonces, para z grande con un signo menos, el comportamiento del SN también se acerca al perceptrón. Y solo cuando w ⋅ x + b tiene un tamaño promedio, se observan serias desviaciones del modelo de perceptrón.

¿Qué pasa con la forma algebraica de σ? ¿Cómo lo entendemos? De hecho, la forma exacta de σ no es tan importante: la forma de la función en el gráfico es importante. Aquí esta:



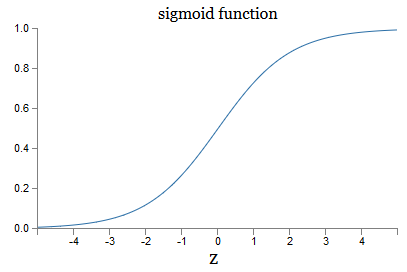
Esta es una versión fluida de la función de paso:



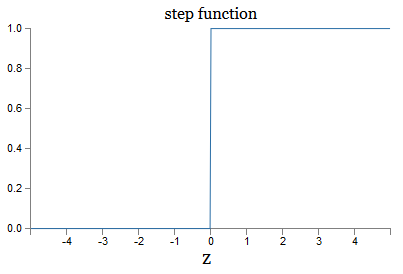
Si σ fuera paso a paso, entonces el SN sería un perceptrón, ya que tendría 0 o 1 salida dependiendo del signo w ⋅ x + b (bueno, de hecho, en z = 0, el perceptrón da 0, y la función de paso 1 , entonces en ese punto, la función tendría que ser cambiada).

Usando la función real σ, obtenemos un perceptrón suavizado. Y lo principal aquí es la suavidad de la función, no su forma exacta. La suavidad significa que pequeños cambios Δw _j pesos y δb compensaciones darán pequeños cambios Δ salida de la salida. El álgebra nos dice que la salida Δ se aproxima bien de la siguiente manera:

$$

$$\ Delta output \ approx \ sum_j \ frac {\ partial output} {\ partial w_j} \ Delta w_j + \ frac {\ partial output} {\ partial b} \ Delta b \ tag {5}$$

Donde la suma es sobre todos los pesos w _j , y ∂output / ∂w _j y ∂output / ∂b denotan derivadas parciales de la salida con respecto a w _j y b, respectivamente. ¡No se asuste si se siente inseguro en compañía de derivados privados! Aunque la fórmula parece complicada, con todas estas derivadas parciales, en realidad dice algo bastante simple (y útil): la salida Δ es una función lineal que depende de los pesos y sesgos Δw _j y Δb. Su linealidad facilita la selección de pequeños cambios en pesos y compensaciones para lograr cualquier sesgo de salida pequeño deseado. Por lo tanto, aunque los SN son similares a los perceptrones en el comportamiento cualitativo, facilitan la comprensión de cómo se puede cambiar la producción cambiando los pesos y los desplazamientos.

Si la forma general σ es importante para nosotros, y no su forma exacta, ¿por qué usamos tal fórmula (3)? De hecho, más adelante a veces consideraremos neuronas cuya salida es f (w ⋅ x + b), donde f () es alguna otra función de activación. Lo principal que cambia cuando cambia la función es el valor de las derivadas parciales en la ecuación (5). Resulta que cuando calculamos estas derivadas parciales, el uso de σ simplifica enormemente el álgebra, ya que los exponentes tienen propiedades muy agradables al diferenciar. En cualquier caso, σ se usa a menudo para trabajar con redes neuronales, y con mayor frecuencia en este libro usaremos dicha función de activación.

¿Cómo interpretar el resultado del trabajo de CH? Obviamente, la principal diferencia entre los perceptrones y el CH es que el CH no da solo 0 o 1. Su salida puede ser cualquier número real de 0 a 1, por lo que valores como 0.173 o 0.689 son válidos. Esto puede ser útil, por ejemplo, si desea que el valor de salida indique, por ejemplo, el brillo promedio de los píxeles de la imagen recibida en la entrada del NS. Pero a veces puede ser inconveniente. Supongamos que queremos que la salida de la red diga que "se ingresó la imagen 9" o "imagen de entrada no 9". Obviamente, sería más fácil si los valores de salida fueran 0 o 1, como un perceptrón. Pero en la práctica, podemos estar de acuerdo en que cualquier valor de salida de al menos 0.5 significaría "9" en la entrada, y cualquier valor inferior a 0.5 significaría que es "no 9". Siempre indicaré explícitamente la existencia de tales acuerdos.

Ejercicios

• Perceptrones simuladores de CH, parte 1

Supongamos que tomamos todos los pesos y desplazamientos de una red de perceptrones, y los multiplicamos por una constante positiva c> 0. Muestre que el comportamiento de la red no cambia.

• Perceptrones simuladores de CH, parte 2

Supongamos que tenemos la misma situación que en el problema anterior: una red de perceptrones. Supongamos también que se seleccionan los datos de entrada para la red. No necesitamos un valor específico, lo principal es que es fijo. Suponga que los pesos y los desplazamientos son tales que w⋅x + b ≠ 0, donde x es el valor de entrada de cualquier perceptrón de la red. Ahora reemplazamos todos los perceptrones en la red con SN, y multiplicamos los pesos y desplazamientos por la constante positiva c> 0. Muestre que en el límite c → ∞ el comportamiento de la red desde el SN será exactamente el mismo que el de las redes de perceptrones. ¿Cómo se violará esta afirmación si para uno de los perceptrones w⋅x + b = 0?

Arquitectura de red neuronal

En la siguiente sección, presentaré una red neuronal capaz de una buena clasificación de números escritos a mano. Antes de eso, es útil explicar la terminología que nos permite señalar diferentes partes de la red. Digamos que tenemos la siguiente red:



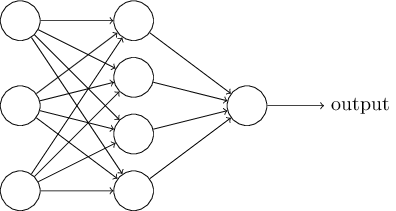
Como mencioné, la capa más a la izquierda de la red se llama capa de entrada, y sus neuronas se llaman neuronas de entrada. La capa de salida más a la derecha contiene neuronas de salida o, como en nuestro caso, una neurona de salida. La capa intermedia se llama oculta, porque sus neuronas no son ni de entrada ni de salida. El término "oculto" puede sonar un poco misterioso; cuando lo escuché por primera vez, decidí que debería tener una importancia filosófica o matemática profunda, sin embargo, solo significa "no entrar y no salir". La red de arriba solo tiene una capa oculta, pero algunas redes tienen varias capas ocultas. Por ejemplo, en la siguiente red de cuatro capas hay dos capas ocultas:



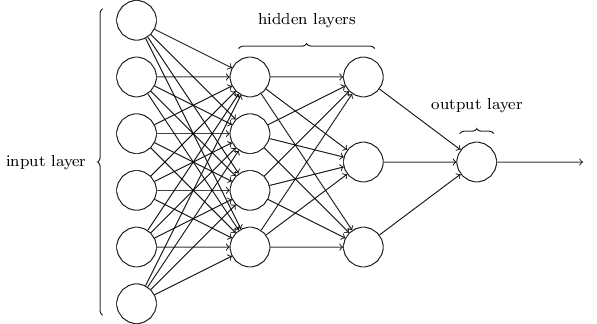
Esto puede ser confuso, pero por razones históricas, tales redes de múltiples capas a veces se denominan perceptrones multicapa, MLP, a pesar de que consisten en neuronas sigmoideas en lugar de perceptrones. No voy a usar esa terminología porque es confusa, pero debo advertir sobre su existencia.

Diseñar capas de entrada y salida a veces es una tarea simple. Por ejemplo, supongamos que estamos tratando de determinar si el número escrito a mano significa "9" o no. Un circuito de red natural codificará el brillo de los píxeles de la imagen en las neuronas de entrada. Si la imagen es en blanco y negro, 64x64 píxeles de tamaño, entonces tendremos 64x64 = 4096 neuronas de entrada, con un brillo en el rango de 0 a 1. La capa de salida contendrá solo una neurona, cuyo valor menor que 0.5 significará que "en la entrada no fue 9 ", pero los valores más significarán que" la entrada fue 9 ".

Y aunque diseñar capas de entrada y salida es a menudo una tarea simple, diseñar capas ocultas puede ser un arte difícil. En particular, no es posible describir el proceso de desarrollo de capas ocultas con unas simples reglas generales. Los investigadores de la Asamblea Nacional han desarrollado muchas reglas heurísticas para el diseño de capas ocultas que ayudan a obtener el comportamiento deseado de las redes neuronales. Por ejemplo, dicha heurística se puede utilizar para comprender cómo lograr un compromiso entre el número de capas ocultas y el tiempo disponible para capacitar a la red. Más adelante nos encontraremos con algunas de estas reglas.

Hasta ahora, hemos estado discutiendo las NS en las que la salida de una capa se usa como entrada para la siguiente. Dichas redes se denominan redes neuronales de distribución directa. Esto significa que no hay bucles en la red: la información siempre avanza y nunca retroalimenta. Si tuviéramos bucles, encontraríamos situaciones en las que el sigmoide de entrada dependería de la salida. Sería difícil de comprender, y no permitimos tales bucles.

Sin embargo, hay otros modelos de NS artificiales en los que es posible usar bucles de retroalimentación. Estos modelos se denominan redes neuronales recurrentes (RNS). La idea de estas redes es que sus neuronas se activan por períodos limitados de tiempo. Esta activación puede estimular otros neutrones, que pueden activarse un poco más tarde, también por un tiempo limitado. Esto conduce a la activación de las siguientes neuronas, y con el tiempo obtenemos una cascada de neuronas activadas. Los bucles en tales modelos no presentan problemas, ya que la salida de una neurona afecta su entrada en un momento posterior, y no de inmediato.

Los RNS no fueron tan influyentes como los NS de distribución directa, en particular porque los algoritmos de entrenamiento para los RNS hasta ahora tienen menos potencial. Sin embargo, el RNS sigue siendo extremadamente interesante. En el espíritu de trabajo, están mucho más cerca del cerebro que NS de distribución directa. Es posible que el RNS pueda resolver problemas importantes que, con la ayuda de la distribución directa NS, pueden resolverse con grandes dificultades. Sin embargo, para limitar el alcance de nuestro estudio, nos concentraremos en el NS de distribución directa más utilizado.

Red simple de clasificación de tinta

Una vez definidas las redes neuronales, volveremos al reconocimiento de escritura a mano. La tarea de reconocer números escritos a mano se puede dividir en dos subtareas. Primero, queremos encontrar una manera de dividir una imagen que contenga muchos dígitos en una secuencia de imágenes individuales, cada una de las cuales contiene un dígito. Por ejemplo, nos gustaría dividir la imagen



en seis separados



Los humanos podemos resolver fácilmente este problema de segmentación, pero es difícil para un programa de computadora dividir correctamente la imagen. Después de la segmentación, el programa necesita clasificar cada dígito individual. Entonces, por ejemplo, queremos que nuestro programa reconozca que el primer dígito



son las 5.

Nos concentraremos en crear un programa para resolver el segundo problema, la clasificación de números individuales. Resulta que el problema de la segmentación no es tan difícil de resolver tan pronto como encontramos una buena manera de clasificar los dígitos individuales. Existen muchos enfoques para resolver el problema de segmentación. Una de ellas es probar muchas formas diferentes de segmentación de imágenes utilizando el clasificador de dígitos individuales, evaluando cada intento. La segmentación de prueba es muy apreciada si el clasificador de dígitos individuales confía en la clasificación de todos los segmentos, y baja si tiene problemas en uno o más segmentos. La idea es que si el clasificador tiene problemas en algún lugar, lo más probable es que la segmentación sea incorrecta. Esta idea y otras opciones se pueden utilizar para una buena solución al problema de segmentación. Entonces, en lugar de preocuparnos por la segmentación, nos concentraremos en desarrollar un NS capaz de resolver una tarea más interesante y compleja, a saber, reconocer números escritos a mano individuales.

Para reconocer dígitos individuales, usaremos NS de tres capas:



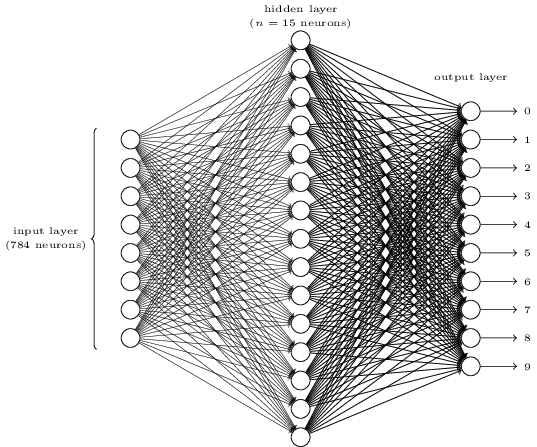
La capa de red de entrada contiene neuronas que codifican varios valores de los píxeles de entrada. Como se indicará en la siguiente sección, nuestros datos de entrenamiento consistirán en muchas imágenes de dígitos escritos a mano escaneados de 28x28 píxeles de tamaño, por lo que la capa de entrada contiene 28x28 = 784 neuronas. Por simplicidad, no indiqué la mayoría de las 784 neuronas en el diagrama. Los píxeles entrantes son en blanco y negro, con un valor de 0.0 que indica blanco, 1.0 que indica negro y valores intermedios que indican sombras de gris cada vez más oscuras.

La segunda capa de la red está oculta. Denotamos el número de neuronas en esta capa n, y experimentaremos con diferentes valores de n. El ejemplo anterior muestra una pequeña capa oculta que contiene solo n = 15 neuronas.

Hay 10 neuronas en la capa de salida de la red. Si la primera neurona está activada, es decir, su valor de salida es ≈ 1, esto indica que la red cree que la entrada fue 0. Si la segunda neurona está activada, la red cree que la entrada fue 1. Y así sucesivamente. Estrictamente hablando, numeramos las neuronas de salida de 0 a 9 y observamos cuál de ellas tenía el valor de activación máximo. Si esto es, digamos, la neurona No. 6, entonces nuestra red cree que la entrada fue el número 6. Y así sucesivamente.

Quizás se pregunte por qué necesitamos usar diez neuronas. Después de todo, queremos saber qué dígito del 0 al 9 corresponde a la imagen de entrada. Sería natural usar solo 4 neuronas de salida, cada una de las cuales tomaría un valor binario, dependiendo de si su valor de salida está más cerca de 0 o 1. Cuatro neuronas serían suficientes, ya que 2 ⁴ = 16, más de 10 valores posibles. ¿Por qué nuestra red debería usar 10 neuronas? ¿Es esto ineficaz? La base para esto es empírica; podemos probar ambas variantes de la red, y resulta que para esta tarea, una red con 10 neuronas de salida está mejor entrenada para reconocer números que una red con 4. Sin embargo, la pregunta sigue siendo, ¿por qué son mejores las 10 neuronas de salida? ¿Hay alguna heurística que nos diga de antemano que se deben usar 10 neuronas de salida en lugar de 4?

Para entender por qué, es útil pensar en lo que hace una red neuronal. Primero, considere la opción con 10 neuronas de salida. Nos centramos en la primera neurona de salida, que está tratando de decidir si la imagen entrante es cero. Lo hace sopesando la evidencia obtenida de una capa oculta. ¿Qué hacen las neuronas ocultas? Supongamos que la primera neurona en la capa oculta determina si hay algo como esto en la imagen:



Puede hacer esto asignando pesos grandes a píxeles que coincidan con esta imagen, y pesos pequeños al resto. Del mismo modo, suponga que las neuronas segunda, tercera y cuarta en la capa oculta están buscando si hay fragmentos similares en la imagen:



Como habrás adivinado, todos estos cuatro fragmentos juntos dan la imagen 0, que vimos anteriormente:



Entonces, si las cuatro neuronas ocultas están activadas, podemos concluir que el número es 0. Por supuesto, esta no es la única evidencia de que 0 se mostró allí; podemos obtener 0 de muchas otras maneras (cambiando ligeramente estas imágenes o distorsionándolas ligeramente). Sin embargo, podemos decir con certeza que, al menos en este caso, podemos concluir que había 0 en la entrada.

Si suponemos que la red funciona así, podemos dar una explicación plausible de por qué es mejor usar 10 neuronas de salida en lugar de 4. Si tuviéramos 4 neuronas de salida, la primera neurona intentaría decidir cuál es el bit más significativo del dígito entrante. Y no hay una manera fácil de asociar el bit más significativo con las formas simples dadas anteriormente. Es difícil imaginar razones históricas por las cuales las partes de la forma de un dígito estarían de alguna manera relacionadas con el bit más significativo de la salida.

Sin embargo, todo lo anterior solo es compatible con la heurística. Nada habla a favor del hecho de que una red de tres capas debería funcionar como dije, y las neuronas ocultas deberían encontrar componentes simples de las formas. Quizás el complicado algoritmo de aprendizaje encuentre algunos pesos que nos permitirán usar solo 4 neuronas de salida. Sin embargo, como método heurístico, mi método funciona bien y puede ahorrarle un tiempo considerable en el desarrollo de una buena arquitectura NS.

Ejercicios

• , . , . . , 3 , ( ) 0,99, 0,01.

Entonces, tenemos el esquema de NA: ¿cómo aprender a reconocer los números? Lo primero que necesitamos son datos de entrenamiento, los llamados conjunto de datos de entrenamiento. Utilizaremos el kit MNIST que contiene decenas de miles de imágenes escaneadas de números escritos a mano y su clasificación correcta. El nombre que recibió MNIST debido a que es un subconjunto modificado de los dos conjuntos de datos recopilados por NIST , el Instituto Nacional de Estándares y Tecnología de EE. UU. Aquí hay algunas imágenes de MNIST:



Estos son los mismos números que se dieron al comienzo del capítulo como tarea de reconocimiento. ¡Por supuesto, cuando revise el NS, le pediremos que reconozca las imágenes incorrectas que ya estaban en el conjunto de entrenamiento!

Los datos de MNIST constan de dos partes. El primero contiene 60,000 imágenes destinadas a la capacitación. Estos son manuscritos escaneados de 250 personas, la mitad de los cuales eran empleados de la Oficina del Censo de los Estados Unidos, y la otra mitad eran estudiantes de secundaria. Las imágenes son en blanco y negro, midiendo 28x28 píxeles. La segunda parte del conjunto de datos MNIST es de 10.000 imágenes para probar la red. Esta también es una imagen en blanco y negro de 28x28 píxeles. Utilizaremos estos datos para evaluar qué tan bien la red ha aprendido a reconocer los números. Para mejorar la calidad de la evaluación, estas cifras fueron tomadas de otras 250 personas que no participaron en la grabación del conjunto de capacitación (aunque también eran empleados de la Oficina y estudiantes de secundaria). Esto nos ayuda a asegurarnos de que nuestro sistema pueda reconocer la escritura a mano de personas que no conoció durante la capacitación.

La entrada de entrenamiento será denotada por x. Será conveniente tratar cada imagen de entrada x como un vector con 28x28 = 784 mediciones. Cada valor dentro del vector indica el brillo de un píxel en la imagen. Denotaremos el valor de salida como y = y (x), donde y es un vector de diez dimensiones. Por ejemplo, si una determinada imagen de entrenamiento x contiene 6, entonces y (x) = (0,0,0,0,0,0,1,0,0,0) ^T será el vector que necesitamos. T es una operación de transposición que convierte un vector de fila en un vector de columna.

Queremos encontrar un algoritmo que nos permita buscar dichos pesos y compensaciones para que la salida de la red se acerque a y (x) para todas las entradas de entrenamiento x. Para cuantificar la aproximación de este objetivo, definimos una función de costo (a veces llamada función de pérdida; en el libro usaremos la función de costo, pero tenga en cuenta otro nombre):

$$

$$C(w, b) = \frac{1}{2n} \sum_x || y(x) – a ||^2 \tag{6}$$

Aquí w denota un conjunto de pesos de red, b es un conjunto de desplazamientos, n es el número de datos de entrada de entrenamiento, a es el vector de datos de salida cuando x son datos de entrada, y la suma pasa a través de toda la entrada de entrenamiento x. La salida, por supuesto, depende de x, w y b, pero por simplicidad no designé esta dependencia. La notación || v || significa la longitud del vector v. Llamaremos a C una función de costo cuadrático; a veces también se denomina error estándar o MSE. Si observa detenidamente C, puede ver que no es negativa, ya que todos los miembros de la suma no son negativos. Además, el costo de C (w, b) se vuelve pequeño, es decir, C (w, b) ≈ 0, precisamente cuando y (x) es aproximadamente igual al vector de salida a para todos los datos de entrada de entrenamiento x. Entonces, nuestro algoritmo funcionó bien si logramos encontrar pesos y compensaciones tales que C (w, b) ≈ 0. Y viceversa, funcionó mal cuando C (w,b) grande: esto significa que y (x) no coincide con la salida para una gran cantidad de entrada. Resulta que el objetivo del algoritmo de entrenamiento es minimizar el costo de C (w, b) en función de los pesos y las compensaciones. En otras palabras, necesitamos encontrar un conjunto de pesos y compensaciones que minimicen el valor del costo. Haremos esto usando un algoritmo llamado descenso de gradiente.

¿Por qué necesitamos un valor cuadrático? ¿No nos interesa principalmente la cantidad de imágenes que la red reconoce correctamente? ¿Es posible simplemente maximizar este número directamente y no minimizar el valor intermedio del valor cuadrático? El problema es que el número de imágenes correctamente reconocidas no es una función uniforme de los pesos y las compensaciones de la red. En su mayor parte, los pequeños cambios en los pesos y las compensaciones no cambiarán el número de imágenes correctamente reconocidas. Debido a esto, es difícil entender cómo cambiar los pesos y los prejuicios para mejorar la eficiencia. Si utilizamos una función de costo uniforme, nos será fácil entender cómo hacer pequeños cambios en los pesos y las compensaciones para mejorar el costo. Por lo tanto, primero nos centraremos en el valor cuadrático y luego estudiaremos la precisión de la clasificación.

Incluso teniendo en cuenta que queremos utilizar una función de costo uniforme, ¿puede que le interese saber por qué elegimos la función cuadrática para la ecuación (6)? ¿No es posible elegirlo arbitrariamente? ¿Quizás si elegimos una función diferente, obtendríamos un conjunto completamente diferente de minimización de pesos y compensaciones? Una pregunta razonable, y luego examinaremos nuevamente la función de costo y haremos algunas correcciones. Sin embargo, la función de costo cuadrático funciona muy bien para comprender las cosas básicas en el aprendizaje de NS, por lo que por ahora nos mantendremos firmes.

Para resumir: nuestro objetivo en el entrenamiento de NS es encontrar pesos y compensaciones que minimicen la función de costo cuadrático C (w, b). La tarea está bien planteada, pero hasta ahora tiene muchas estructuras de distracción: la interpretación de w y b como pesos y compensaciones, la función σ oculta en el fondo, la elección de la arquitectura de red, MNIST, etc. Resulta que podemos entender mucho, ignorando la mayor parte de esta estructura y concentrándonos solo en el aspecto de la minimización. Entonces, por ahora, nos olvidaremos de la forma especial de la función de costos, la comunicación con la Asamblea Nacional, etc. En cambio, vamos a imaginar que solo tenemos una función con muchas variables y queremos minimizarla. Desarrollaremos una tecnología llamada descenso de gradiente, que puede usarse para resolver tales problemas. Y luego volvemos a una cierta función,que queremos minimizar para la Asamblea Nacional.

Bueno, digamos que estamos tratando de minimizar alguna función C (v). Puede ser cualquier función con valores reales de muchas variables v = v ₁ , v ₂ , ... Tenga en cuenta que reemplacé la notación w y b por v para mostrar que puede ser cualquier función: ya no estamos obsesionados con HC. Es útil imaginar que una función C tiene solo dos variables: v ₁ y v ₂ :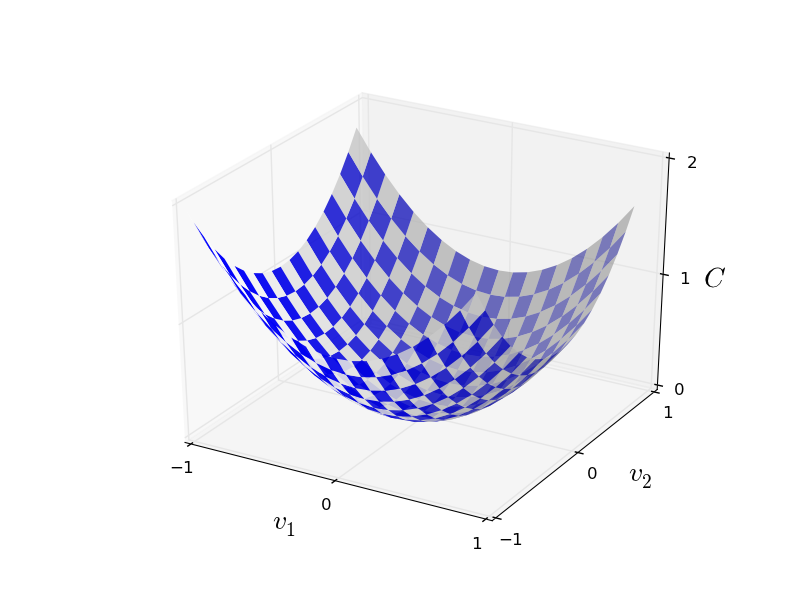



Nos gustaría encontrar dónde C alcanza un mínimo global. Por supuesto, con la función dibujada arriba, podemos estudiar el gráfico y encontrar el mínimo. En este sentido, ¡puedo haberte dado una función demasiado simple! En el caso general, C puede ser una función compleja de muchas variables, y generalmente es imposible simplemente mirar el gráfico y encontrar el mínimo.

Una forma de resolver el problema es usar álgebra para encontrar el mínimo analíticamente. Podemos calcular las derivadas e intentar usarlas para encontrar el extremo. Si tenemos suerte, esto funcionará cuando C sea una función de una o dos variables. Pero con una gran cantidad de variables, esto se convierte en una pesadilla. Y para las NS, a menudo necesitamos muchas más variables: para las NS más grandes, las funciones de costo de una manera compleja dependen de miles de millones de pesos y desplazamientos. ¡Usar álgebra para minimizar estas funciones fallará!

(Habiendo declarado que sería más conveniente para nosotros considerar C como una función de dos variables, dije dos veces en dos párrafos "sí, pero ¿y si es una función de un número mucho mayor de variables?" Pido disculpas. Créenos que realmente será útil representar C como una función dos variables, es solo que a veces esta imagen se desmorona, por eso se necesitaban los dos párrafos anteriores. Para el razonamiento matemático, a menudo es necesario hacer malabarismos con varias representaciones intuitivas, aprendiendo al mismo tiempo cuándo se puede usar la representación y cuándo no zya).

Bien, eso significa que el álgebra no funcionará. Afortunadamente, existe una gran analogía que ofrece un algoritmo que funciona bien. Imaginamos nuestra función como algo así como un valle. Con el último horario, no será tan difícil de hacer. E imaginamos una pelota rodando por la ladera del valle. Nuestra experiencia nos dice que la pelota finalmente se deslizará hasta el fondo. ¿Quizás podemos usar esta idea para encontrar el mínimo de una función? Seleccionamos al azar el punto de partida para una pelota imaginaria y luego simulamos el movimiento de la pelota, como si estuviera rodando hacia el fondo del valle. Podemos usar esta simulación simplemente contando las derivadas (y, posiblemente, las segundas derivadas) de C: nos contarán todo sobre la forma local del valle y, por lo tanto, sobre cómo rodará nuestra bola.

Según lo que escribiste, podrías pensar que escribiremos las ecuaciones de movimiento de Newton para la pelota, consideraremos los efectos de la fricción y la gravedad, y así sucesivamente. De hecho, no estaremos tan cerca de seguir esta analogía con la pelota: ¡estamos desarrollando un algoritmo para minimizar C y no una simulación exacta de las leyes de la física! Esta analogía debería estimular nuestra imaginación y no limitar nuestro pensamiento. Entonces, en lugar de sumergirnos en los detalles complejos de la física, hagamos la pregunta: si fuéramos nombrados dios por un día, y creáramos nuestras propias leyes de la física, diciéndole a la pelota cómo rodar qué ley o las leyes de movimiento elegiríamos, para que la pelota siempre ruede sobre fondo del valle?

Para aclarar el problema, pensaremos en lo que sucede si movemos la pelota una pequeña distancia Δv ₁ en la dirección de v ₁, y una pequeña distancia Δv ₂ en la dirección de v ₂ . El álgebra nos dice que C cambia de la siguiente manera:

$$

$$\Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2 \tag{7}$$

Encontraremos una manera de elegir tales Δv ₁ y Δv ₂ para que ΔC sea menor que cero; es decir, los seleccionaremos para que la bola ruede hacia abajo. Para comprender cómo hacer esto, es útil definir Δv como el vector de cambios, es decir, Δv ≡ (Δv ₁ , Δv ₂ ) ^T , donde T es la operación de transposición que convierte los vectores de fila en vectores de columna. También definimos el vector gradiente de C como derivados parciales (∂S / ∂V ₁ , ∂S / ∂V ₂ ) ^T . Denotamos el vector gradiente por ∇:

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2})^T \tag{8}$$

Pronto reescribiremos el cambio en ΔC a través de Δv y el gradiente ∇C. Mientras tanto, quiero aclarar algo, por lo que las personas a menudo cuelgan del gradiente. Cuando se encontraron por primera vez con ∇C, las personas a veces no entienden cómo deberían percibir el símbolo ∇. ¿Qué significa específicamente? De hecho, puede considerar con seguridad ∇C un único objeto matemático, un vector previamente definido, que simplemente se escribe con dos caracteres. Desde este punto de vista, ∇ es como agitar una bandera que informa que "∇C es un vector de gradiente". Existen puntos de vista más avanzados desde los cuales ∇ puede considerarse como una entidad matemática independiente (por ejemplo, como un operador de diferenciación), pero no los necesitamos.

Con tales definiciones, la expresión (7) puede reescribirse como:

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{9}$$

Esta ecuación ayuda a explicar por qué ∇C se llama un vector de gradiente: conecta los cambios en v con los cambios en C, tal como se espera de una entidad llamada gradiente. [eng. gradiente - desviación / aprox. transl.] Sin embargo, es más interesante que esta ecuación nos permita ver cómo elegir Δv para que ΔC sea negativo. Digamos que elegimos

$$

$$\Delta v = - \eta \nabla C \tag{10}$$

donde η es un pequeño parámetro positivo (velocidad de aprendizaje). Entonces la ecuación (9) nos dice que ΔC ≈ - η ∇C ⋅ ∇C = - η || ∇C || ² . Desde || ∇C || ² ≥ 0, esto asegura que ΔC ≤ 0, es decir, C disminuirá todo el tiempo si cambiamos v, como se prescribe en (10) (por supuesto, como parte de la aproximación de la ecuación (9)). ¡Y esto es exactamente lo que necesitamos! Por lo tanto, tomamos la ecuación (10) para determinar la "ley de movimiento" de la pelota en nuestro algoritmo de descenso de gradiente. Es decir, utilizaremos la ecuación (10) para calcular el valor de Δv, y luego moveremos la pelota a este valor:

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{11}$$

Luego, nuevamente aplicamos esta regla para el próximo movimiento. Continuando con la repetición, bajaremos C hasta que, con suerte, alcancemos un mínimo global.

En resumen, el descenso del gradiente funciona a través del cálculo secuencial del gradiente ∇ C, y el desplazamiento posterior en la dirección opuesta, lo que conduce a una "caída" a lo largo de la pendiente del valle. Esto se puede visualizar de la siguiente manera: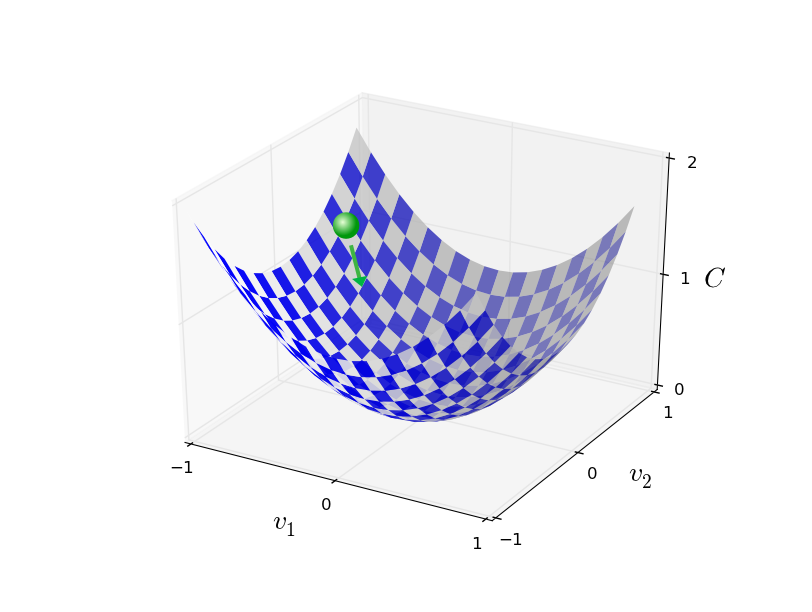



Tenga en cuenta que con esta regla, el descenso de gradiente no reproduce el movimiento físico real. En la vida real, la pelota tiene un impulso que puede permitirle rodar por la pendiente, o incluso rodar por algún tiempo. Solo después del trabajo de la fuerza de fricción se garantiza que la bola ruede por el valle. Nuestra regla de selección Δv solo dice "baja". ¡Una regla bastante buena para encontrar el mínimo!

Para que el descenso de gradiente funcione correctamente, debemos elegir un valor suficientemente pequeño de la velocidad de aprendizaje η para que la ecuación (9) sea una buena aproximación. De lo contrario, puede resultar que ΔC> 0 - ¡nada bueno! Al mismo tiempo, no es necesario que η sea demasiado pequeño, ya que los cambios en Δv serán pequeños y el algoritmo funcionará muy lentamente. En la práctica, η cambia de modo que la ecuación (9) da una buena aproximación y el algoritmo no funciona muy lentamente. Más adelante veremos cómo funciona.

Le expliqué el descenso del gradiente cuando la función C dependía solo de dos variables. Pero todo funciona de la misma manera si C es una función de muchas variables. Supongamos que tiene m variables, v ₁ , ..., v _m. Entonces, el cambio en ΔC causado por un pequeño cambio en Δv = (Δv ₁ , ..., Δv _m ) ^T será

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{12}$$

donde el gradiente ∇C es el vector

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1},…, \frac{\partial C}{\partial v_m})^T \tag{13}$$

Al igual que con dos variables, podemos elegir

$$

$$\Delta v = - \eta \nabla C \tag{14}$$

y asegúrese de que nuestra expresión aproximada (12) para ΔC sea negativa. Esto nos da una forma de ir al mínimo a lo largo del gradiente, incluso cuando C es una función de muchas variables, aplicando la regla de actualización una y otra vez.

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{15}$$

Esta regla de actualización puede considerarse el algoritmo definitorio de descenso de gradiente. Nos da un método para cambiar repetidamente la posición de v en busca del mínimo de la función C. Esta regla no siempre funciona: varias cosas pueden salir mal, evitando que el descenso del gradiente encuentre el mínimo global de C - volveremos a este punto en los siguientes capítulos. Pero en la práctica, el descenso de gradiente a menudo funciona muy bien, y veremos que en la Asamblea Nacional esta es una forma efectiva de minimizar la función de costos y, por lo tanto, capacitar a la red.

En cierto sentido, el descenso de gradiente puede considerarse la estrategia de búsqueda mínima óptima. Supongamos que estamos tratando de mover Δv a una posición para minimizar C. Esto es equivalente a minimizar ΔC ≈ ∇C ⋅ Δv. Limitaremos el tamaño del paso para que || Δv || = ε para alguna pequeña constante ε> 0. En otras palabras, queremos mover una pequeña distancia de un tamaño fijo, y tratar de encontrar la dirección del movimiento que disminuya C tanto como sea posible. Se puede demostrar que la elección de Δv minimizando ∇C ⋅ Δv es Δv = -η∇C, donde η = ε / || ∇C || está determinada por la restricción || Δv || = ε. Por lo tanto, el descenso de gradiente puede considerarse una forma de dar pequeños pasos en la dirección que disminuye más C.

Ejercicios

• . : — , , , .
• , , . , ? ?

Las personas han estudiado muchas opciones para el descenso en gradiente, incluidas aquellas que reproducen con mayor precisión una pelota física real. Dichas opciones tienen sus ventajas, pero también un gran inconveniente: la necesidad de calcular las segundas derivadas parciales de C, que pueden consumir muchos recursos. Para comprender esto, supongamos que necesitamos calcular todas las segundas derivadas parciales ∂ ² C / ∂v _j ∂v _k . Si las variables v _{j son} millones, entonces necesitamos calcular aproximadamente un billón (un millón al cuadrado) de las segundas derivadas parciales (en realidad, medio billón, ya que ∂ ² C / ∂v _j ∂v _k = ∂ ² C / ∂v _k ∂v _j. Pero capturaste la esencia). Esto requerirá muchos recursos informáticos. Hay trucos para evitar esto, y la búsqueda de alternativas al descenso de gradiente es un área de investigación activa. Sin embargo, en este libro usaremos el descenso de gradiente y sus variantes como el enfoque principal para aprender NS.

¿Cómo aplicamos el gradiente descendente al aprendizaje de NA? Necesitamos usarlo para buscar pesos w _k y compensaciones b _l que minimicen la ecuación de costos (6). Reescribamos la regla de actualización de descenso de gradiente reemplazando las variables _vj con pesos y compensaciones. En otras palabras, ahora nuestra "posición" tiene los componentes w _k y b _l , y el vector gradiente ∇C tiene los componentes correspondientes ∂C / ∂w_k y ∂C / ∂b _l . Habiendo escrito nuestra regla de actualización con nuevos componentes, obtenemos:

$$

$$w_k \rightarrow w'_k = w_k - \eta \frac{\partial C}{\partial w_k} \tag{16}$$

$$

$$b_l \rightarrow b'_l = b_l - \eta \frac{\partial C}{\partial b_l} \tag{17}$$

Al volver a aplicar esta regla de actualización, podemos "rodar cuesta abajo" y, con un poco de suerte, encontrar la función de costo mínimo. En otras palabras, esta regla puede usarse para entrenar a la Asamblea Nacional.

Existen varios obstáculos para aplicar la regla de descenso de gradiente. Los estudiaremos con más detalle en los siguientes capítulos. Pero por ahora, quiero mencionar solo un problema. Para entenderlo, volvamos al valor cuadrático en la ecuación (6). Tenga en cuenta que esta función de costo se parece a C = 1 / n ∑ _x C _x , es decir, es el costo promedio C _x ≡ (|| y (x) −a || ² ) / 2 para ejemplos de capacitación individual. En la práctica, para calcular el gradiente ∇C necesitamos calcular los gradientes ∇C _xpor separado para cada entrada de entrenamiento x, y luego promediarlos, ∇C = 1 / n ∑ _x ∇C _x . Desafortunadamente, cuando la cantidad de entrada será muy grande, tomará mucho tiempo y dicha capacitación será lenta.

Para acelerar el aprendizaje, puede usar el descenso de gradiente estocástico. La idea es calcular aproximadamente el gradiente de ∇C calculando ∇C _x para una pequeña muestra aleatoria de entrada de entrenamiento. Al calcular su promedio, podemos obtener rápidamente una buena estimación del gradiente verdadero ∇C, y esto ayuda a acelerar el descenso del gradiente y, por lo tanto, al entrenamiento.

Al formular con mayor precisión, el descenso de gradiente estocástico funciona mediante un muestreo aleatorio de un pequeño número de m datos de entrada de entrenamiento. Llamaremos a estos datos aleatorios X ₁ , X ₂ , .., X _m , y lo llamaremos un mini paquete. Si el tamaño de la muestra m es lo suficientemente grande, el valor promedio de ∇C _{X j} será lo suficientemente cercano al promedio de todos los ∇Cx, es decir

$$

$$\frac{\sum^m_{j=1} \nabla C_{X_j}}{m} \approx \frac{\sum_x \nabla C_x}{n} = \nabla C \tag{18}$$

donde la segunda cantidad va sobre todo el conjunto de datos de entrenamiento. Al intercambiar partes, obtenemos

$$

$$\nabla C \approx \frac{1}{m} \sum^m_{j=1} \nabla C_{X_j} \tag{19}$$

lo que confirma que podemos estimar el gradiente general calculando los gradientes para un minipack seleccionado al azar.

Para relacionar esto directamente con el entrenamiento de NS, supongamos que w _k y b _l denotan los pesos y desplazamientos de nuestro NS. Luego, el descenso de gradiente estocástico selecciona un mini paquete aleatorio de datos de entrada y aprende de ellos

$$

$$w_k \rightarrow w'_k = w_k - \frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial w_k} \tag{20}$$

$$

$$b_l \rightarrow b'_l = b_l - \frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial b_l} \tag{21}$$

donde es la suma de todos los ejemplos de entrenamiento X _j en el minipaquete actual. Luego seleccionamos otro mini-paquete al azar y estudiamos en él. Y así sucesivamente, hasta agotar todos los datos de entrenamiento, lo que se llama el final de la era de entrenamiento. En este momento, estamos comenzando de nuevo una nueva era de aprendizaje.

Por cierto, vale la pena señalar que los acuerdos sobre el escalado de la función de costos y la actualización de los pesos y las compensaciones difieren en un mini paquete. En la ecuación (6), escalamos la función de costo 1 / n veces. A veces las personas omiten 1 / n al sumar los costos de los ejemplos de capacitación individual, en lugar de calcular el promedio. Esto es útil cuando el número total de ejemplos de entrenamiento no se conoce de antemano. Esto puede suceder, por ejemplo, cuando aparecen datos adicionales en tiempo real. Del mismo modo, las reglas de actualización de mini-paquete (20) y (21) a veces omiten el miembro de 1 / m delante de la suma. Conceptualmente, esto no afecta nada, ya que es equivalente a un cambio en la velocidad de aprendizaje η. Sin embargo, vale la pena prestar atención al comparar varios trabajos.

Un descenso de gradiente estocástico puede considerarse como un voto político: es mucho más fácil tomar una muestra en forma de un mini paquete que aplicar un descenso de gradiente a una muestra completa, al igual que una encuesta a la salida de un sitio es más fácil que realizar una elección completa. Por ejemplo, si nuestro conjunto de entrenamiento tiene un tamaño de n = 60,000, como MNIST, y hacemos una muestra de un mini paquete de tamaño m = 10, ¡entonces aceleraremos la estimación del gradiente 6000 veces! Por supuesto, la estimación no será ideal, habrá fluctuaciones estadísticas, pero no es necesario que sea ideal: solo necesitamos movernos en la dirección que disminuye C, lo que significa que no necesitamos calcular el gradiente con precisión. En la práctica, el descenso gradiente estocástico es una técnica de enseñanza común y poderosa para la Asamblea Nacional, y la base de la mayoría de las tecnologías de enseñanza que desarrollaremos como parte del libro.

• - 1. , x w _k → w′ _k = w _k − η ∂C _x / ∂w _k b _l → b′ _l = b _l − η ∂C _x / ∂b _l . . Y así sucesivamente. , -, . - ( ). - - 20.

Permítanme terminar esta sección con una discusión sobre un tema que a veces molesta a las personas que primero han encontrado un descenso de gradiente. En NS, el valor de C es una función de muchas variables (todos los pesos y compensaciones) y, en cierto sentido, determina la superficie en un espacio muy multidimensional. La gente comienza a pensar: "Tendré que visualizar todas estas dimensiones adicionales". Y comienzan a preocuparse: "No puedo navegar en cuatro dimensiones, sin mencionar cinco (o cinco millones)". ¿Tienen alguna cualidad especial que tienen las supermatemáticas "reales"? Por supuesto que no. Incluso los matemáticos profesionales no pueden visualizar el espacio de cuatro dimensiones bastante bien, si es que lo hacen. Van a trucos, desarrollando otras formas de representar lo que está sucediendo. Esto es exactamente lo que hicimos:Utilizamos la representación algebraica (en lugar de visual) de ΔC para comprender cómo moverse para que C disminuya. Las personas que hacen un buen trabajo con una gran cantidad de dimensiones tienen en mente una gran biblioteca de técnicas similares; Nuestro truco algebraico es solo un ejemplo. Puede que estas técnicas no sean tan simples como estamos acostumbrados al visualizar tres dimensiones, pero cuando crea una biblioteca de técnicas similares, comienza a pensar bien en dimensiones superiores. No entraré en detalles, pero si está interesado, puede que le gustea qué estamos acostumbrados cuando visualizamos tres dimensiones, pero cuando creas una biblioteca de técnicas similares, comienzas a pensar bien en dimensiones superiores. No entraré en detalles, pero si está interesado, puede que le gustea qué estamos acostumbrados cuando visualizamos tres dimensiones, pero cuando creas una biblioteca de técnicas similares, comienzas a pensar bien en dimensiones superiores. No entraré en detalles, pero si está interesado, puede que le gusteUna discusión de algunas de estas técnicas por matemáticos profesionales que están acostumbrados a pensar en dimensiones superiores. Aunque algunas de las técnicas discutidas son bastante complejas, la mayoría de las mejores respuestas son intuitivas y accesibles para todos.

Implementación de una red para clasificar números

Bien, ahora escribamos un programa que aprenda a reconocer los dígitos escritos a mano utilizando el descenso de gradiente estocástico y los datos de entrenamiento de MNIST. ¡Haremos esto con un programa corto en Python 2.7 que consta de solo 74 líneas! Lo primero que necesitamos es descargar los datos de MNIST. Si usa git, puede obtenerlos clonando el repositorio de este libro:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git

Si no, descargue el código desde el enlace .

Por cierto, cuando mencioné los datos de MNIST anteriormente, dije que están divididos en 60,000 imágenes de entrenamiento y 10,000 imágenes de prueba. Esta es la descripción oficial de MNIST. Romperemos los datos de manera un poco diferente. Dejaremos las imágenes de verificación sin cambios, pero dividiremos el conjunto de capacitación en dos partes: 50,000 imágenes, que usaremos para capacitar a la Asamblea Nacional, e 10,000 imágenes individuales para confirmación adicional. Si bien no los utilizaremos, más adelante nos serán útiles cuando comprendamos la configuración de algunos hiperparámetros del NS, la velocidad de aprendizaje, etc., que nuestro algoritmo no selecciona directamente. Aunque los datos que corroboran no son parte de la especificación MNIST original, muchos usan MNIST de esta manera, y en el campo de HC el uso de datos corroborantes es común. Ahora, hablando de los "datos de entrenamiento MNIST", me referiré a nuestros 50,000 karitnoks, no los 60,000 originales.

Además de los datos MNIST, también necesitamos una biblioteca de Python llamada Numpy para cálculos rápidos de álgebra lineal. Si no lo tiene, puede tomarlo desde el enlace .

Antes de darle todo el programa, permítame explicarle las características principales del código para NS. El lugar central está ocupado por la clase Red, que usamos para representar a la Asamblea Nacional. Aquí está el código de inicialización para el objeto de red:

 class Network(object): def __init__(self, sizes): self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] 

La matriz de tamaños contiene el número de neuronas en las capas correspondientes. Entonces, si queremos crear un objeto de red con dos neuronas en la primera capa, tres neuronas en la segunda capa y una neurona en la tercera, entonces lo escribiremos así:

 net = Network([2, 3, 1]) 

Las compensaciones y los pesos en el objeto Red se inicializan aleatoriamente utilizando la función numpy np.random.randn, que genera una distribución gaussiana con una expectativa matemática de 0 y una desviación estándar de 1. Esta inicialización aleatoria le da a nuestro algoritmo de descenso de gradiente estocástico un punto de partida. En los siguientes capítulos encontraremos las mejores formas de inicializar pesos y compensaciones, pero por ahora esto es suficiente. Tenga en cuenta que el código de inicialización de la red supone que se ingresará la primera capa de neuronas, y no les asigna un sesgo, ya que solo se usan para calcular la salida.

También tenga en cuenta que las compensaciones y los pesos se almacenan como una matriz de matrices Numpy. Por ejemplo, net.weights [1] es una matriz de Numpy que almacena los pesos que conectan las capas segunda y tercera de las neuronas (esta no es la primera y la segunda capa, ya que en Python la numeración de los elementos de la matriz proviene de cero). Como tomará demasiado tiempo escribir net.weights [1], denotamos esta matriz como w. Esta es una matriz tal que w _jk es el peso de la conexión entre la kth neurona en la segunda capa y la jth neurona en la tercera. Tal orden de índices j y k puede parecer extraño, ¿no sería más lógico intercambiarlos? Pero la gran ventaja de tal registro es que se obtiene el vector de activación de la tercera capa de neuronas:

$$

$$a '= \ sigma (wa + b) \ tag {22}$$

Veamos esta ecuación bastante rica. a es el vector de activación de la segunda capa de neuronas. Para obtener a ', multiplicamos a por la matriz de peso w, y sumamos el vector de desplazamiento b. Luego aplicamos el elemento sigmoide σ elemento por elemento a cada elemento del vector wa + b (esto se llama vectorización de la función σ). Es fácil verificar que la ecuación (22) da el mismo resultado que la regla (4) para calcular una neurona sigmoidea.

Ejercicio

• Escriba la ecuación (22) en forma de componente y asegúrese de que da el mismo resultado que la regla (4) para calcular una neurona sigmoidea.

Con todo esto en mente, es fácil escribir código que calcule la salida de un objeto de red. Comenzamos definiendo un sigmoide:

 def sigmoid(z): return 1.0/(1.0+np.exp(-z)) 

Tenga en cuenta que cuando el parámetro z es un vector o matriz de Numpy, Numpy aplicará automáticamente el elemento sigmoide en cuanto a elementos, es decir, en forma de vector.

Agregue un método de propagación directa a la clase de red, que toma una entrada de la red como entrada y devuelve la salida correspondiente. Se supone que el parámetro a es (n, 1) Numpy ndarray, no un vector (n,). Aquí n es el número de neuronas de entrada. Si intenta usar el vector (n,), obtendrá resultados extraños.

El método simplemente aplica la ecuación (22) a cada capa:

  def feedforward(self, a): """       "a"""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a 

Por supuesto, básicamente los objetos de la red los necesitamos para aprender. Para hacer esto, les daremos el método SGD, que implementa el descenso de gradiente estocástico. Aquí está su código. En algunos lugares es bastante misterioso, pero a continuación lo analizaremos con más detalle.

  def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) 

training_data es una lista de tuplas "(x, y)" que representan la entrada de entrenamiento y la salida deseada. Las variables epochs y mini_batch_size son el número de epochs para aprender y el tamaño de los mini-paquetes para usar. eta - velocidad de aprendizaje, η. Si test_data está configurado, la red se evaluará con los datos de verificación después de cada era, y se mostrará el progreso actual. Esto es útil para seguir el progreso, pero ralentiza significativamente el trabajo.

El código funciona así. En cada era, comienza mezclando accidentalmente datos de entrenamiento y luego los divide en mini paquetes del tamaño correcto. Esta es una manera fácil de crear una muestra de datos de entrenamiento. Luego, para cada mini_batch aplicamos un paso de descenso de gradiente. Esto se realiza mediante el código self.update_mini_batch (mini_batch, eta), que actualiza los pesos y las compensaciones de la red de acuerdo con una iteración del descenso del gradiente utilizando solo datos de entrenamiento en mini_batch. Aquí está el código para el método update_mini_batch:

  def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] 

La mayor parte del trabajo se realiza por línea.

  delta_nabla_b, delta_nabla_w = self.backprop(x, y) 

Invoca un algoritmo de retropropagación, una forma rápida de calcular el gradiente de una función de costo. Así que update_mini_batch simplemente calcula estos gradientes para cada ejemplo de entrenamiento de mini_batch, y luego actualiza self.weights y self.biases.

Hasta ahora, no demostraré código para self.backprop. Aprenderemos sobre la retropropagación en el próximo capítulo, y habrá un código self.backprop. Por ahora, suponga que se comporta como se indica, devolviendo un gradiente apropiado para el costo asociado con el ejemplo de capacitación x.

Veamos todo el programa, incluidos los comentarios explicativos. Con la excepción de la función self.backprop, el programa habla por sí mismo: el trabajo principal lo realizan self.SGD y self.update_mini_batch. El método self.backprop utiliza varias funciones adicionales para calcular el gradiente, a saber, sigmoid_prime, que calcula la derivada del sigmoid, y self.cost_derivative, que no describiré aquí. Puede hacerse una idea de ellos mirando el código y los comentarios. En el próximo capítulo los consideraremos con más detalle. Tenga en cuenta que si bien el programa parece largo, la mayor parte del código son comentarios que hacen que sea más fácil de entender. De hecho, el programa en sí consta de solo 74 líneas de código que no están vacías ni comentarios. Todo el código está disponible en GitHub .

 """ network.py ~~~~~~~~~~           .      .     ,    .   ,       . """ ####  #   import random #   import numpy as np class Network(object): def __init__(self, sizes): """  sizes      .  ,      Network      ,     ,     ,    ,  [2, 3, 1].               0    1. ,      ,       ,        . """ self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] def feedforward(self, a): """   ,  ``a`` -  .""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): """  ``(nabla_b, nabla_w)``,      C_x. ``nabla_b``  ``nabla_w`` -    numpy,   ``self.biases`` and ``self.weights``.""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #   activation = x activations = [x] #      zs = [] #     z- for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) #   delta = self.cost_derivative(activations[-1], y) * \ sigmoid_prime(zs[-1]) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) """ l      ,      . l = 1    , l = 2 – ,   .    ,   python      .""" for l in xrange(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def evaluate(self, test_data): """    ,      .    –          .""" test_results = [(np.argmax(self.feedforward(x)), y) for (x, y) in test_data] return sum(int(x == y) for (x, y) in test_results) def cost_derivative(self, output_activations, y): """    ( C_x /  a)   .""" return (output_activations-y) ####   def sigmoid(z): """.""" return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): """ .""" return sigmoid(z)*(1-sigmoid(z)) 

¿Qué tan bien reconoce el programa los números escritos a mano? Comencemos cargando los datos MNIST. Haremos esto usando el pequeño programa auxiliar mnist_loader.py, que describiré a continuación. Ejecute los siguientes comandos en el shell de Python:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Esto, por supuesto, se puede hacer en un programa separado, pero si trabaja en paralelo con un libro, será más fácil.

Después de descargar los datos de MNIST, configure una red de 30 neuronas ocultas. Haremos esto después de importar el programa descrito anteriormente, que se llama red:

 >>> import network >>> net = network.Network([784, 30, 10]) 

Finalmente, utilizamos el descenso de gradiente estocástico para el entrenamiento en datos de entrenamiento para 30 eras, con un tamaño de mini paquete de 10 y una velocidad de aprendizaje de η = 3.0:

 >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

Si está ejecutando código en paralelo con la lectura de un libro, tenga en cuenta que la ejecución tardará varios minutos. Le sugiero que comience todo, continúe leyendo y verifique periódicamente lo que produce el programa. Si tiene prisa, puede reducir la cantidad de eras reduciendo la cantidad de neuronas ocultas o utilizando solo una parte de los datos de entrenamiento. El código de trabajo final funcionará más rápido: ¡estos scripts de Python están diseñados para hacerle entender cómo funciona la red y no son de alto rendimiento! Y, por supuesto, después de la capacitación, la red puede funcionar muy rápidamente en casi cualquier plataforma informática. Por ejemplo, cuando enseñamos a la red una buena selección de pesos y compensaciones, se puede portar fácilmente para trabajar en JavaScript en un navegador web o como una aplicación nativa en un dispositivo móvil. En cualquier caso, el programa que entrena la red neuronal hace aproximadamente la misma conclusión. Ella escribe el número de imágenes de prueba correctamente reconocidas después de cada era de entrenamiento. Como puede ver, incluso después de una era, alcanza una precisión de 9,129 de 10,000, y este número continúa creciendo:

Epoch 0: 9129 / 10000
Epoch 1: 9295 / 10000
Epoch 2: 9348 / 10000
...
Epoch 27: 9528 / 10000
Epoch 28: 9542 / 10000
Epoch 29: 9534 / 10000

¡Resulta que la red entrenada da un porcentaje de clasificación correcta de aproximadamente 95 - 95.42% como máximo! Un primer intento bastante prometedor. Le advierto que su código no necesariamente producirá exactamente los mismos resultados, ya que inicializamos la red con ponderaciones y compensaciones aleatorias. Para este capítulo, he elegido el mejor de tres intentos.

Reiniciemos el experimento cambiando el número de neuronas ocultas a 100. Como antes, si ejecuta el código al mismo tiempo que lee, tenga en cuenta que lleva bastante tiempo (en mi máquina, cada era toma varias decenas de segundos), por lo que es mejor leer en paralelo con ejecución de código.

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

Naturalmente, esto mejora el resultado al 96.59%. Al menos en este caso, usar más neuronas ocultas ayuda a obtener mejores resultados.

Los comentarios de los lectores sugieren que los resultados de este experimento varían mucho y que algunos resultados de aprendizaje son mucho peores. Usando técnicas del Capítulo 3 para reducir seriamente la diversidad de la eficiencia del trabajo de una carrera a otra.

Por supuesto, para lograr tal precisión, tuve que elegir un cierto número de eras para aprender, el tamaño del mini paquete y la velocidad de aprendizaje η. Como mencioné anteriormente, se denominan hiperparámetros de nuestra Asamblea Nacional, para distinguirlos de los parámetros simples (pesos y compensaciones) que el algoritmo ajusta durante el entrenamiento. Si elegimos mal los hiperparámetros, obtendremos malos resultados. Supongamos, por ejemplo, que hemos elegido la tasa de aprendizaje η = 0.001:

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data) 

Los resultados son mucho menos impresionantes:

Epoch 0: 1139 / 10000
Epoch 1: 1136 / 10000
Epoch 2: 1135 / 10000
...
Epoch 27: 2101 / 10000
Epoch 28: 2123 / 10000
Epoch 29: 2142 / 10000

Sin embargo, puede ver que la eficiencia de la red crece lentamente con el tiempo. Esto sugiere que puede intentar aumentar la velocidad de aprendizaje, por ejemplo, a 0.01. En este caso, los resultados serán mejores, lo que indica la necesidad de aumentar aún más la velocidad (si el cambio mejora la situación, ¡cambie más!). Si hace esto varias veces, finalmente llegaremos a η = 1.0 (y a veces incluso 3.0), que está cerca de nuestros experimentos anteriores. Entonces, aunque inicialmente seleccionamos mal los hiperparámetros, al menos reunimos suficiente información para poder mejorar nuestra elección de parámetros.

En general, la depuración de NA es un asunto complicado. Esto es especialmente cierto cuando la elección de hiperparámetros iniciales produce resultados que no exceden el ruido aleatorio. Supongamos que intentamos usar una arquitectura exitosa de 30 neuronas, pero cambiamos la velocidad de aprendizaje a 100.0:

 >>> net = network.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 100.0, test_data=test_data) 

Al final, resulta que fuimos demasiado lejos y tomamos demasiada velocidad:

Epoch 0: 1009 / 10000
Epoch 1: 1009 / 10000
Epoch 2: 1009 / 10000
Epoch 3: 1009 / 10000
...
Epoch 27: 982 / 10000
Epoch 28: 982 / 10000
Epoch 29: 982 / 10000

Ahora imagine que nos estamos acercando a esta tarea por primera vez. Por supuesto, sabemos por los primeros experimentos que sería correcto reducir la velocidad de aprendizaje. Pero si tuviéramos que abordar esta tarea por primera vez, no tendríamos resultados que pudieran llevarnos a la solución correcta. ¿Podríamos comenzar a pensar que quizás hemos elegido los parámetros iniciales incorrectos para los pesos y las compensaciones, y que es difícil para la red aprender? ¿O tal vez no tenemos suficientes datos de entrenamiento para obtener un resultado significativo? ¿Quizás no esperamos suficientes eras? ¿Quizás una red neuronal con tal arquitectura simplemente no puede aprender a reconocer números escritos a mano? ¿Quizás la velocidad de aprendizaje es demasiado lenta? Cuando abordas la tarea por primera vez, nunca tienes confianza.

De esto vale la pena aprender una lección de que depurar NS no es una tarea trivial, y esto, como la programación regular, es parte del arte. Debe aprender este arte de depuración para obtener buenos resultados de NS. En general, necesitamos desarrollar una heurística para seleccionar buenos hiperparámetros y buena arquitectura. Discutiremos esto en detalle en el libro, incluyendo cómo seleccioné los hiperparámetros anteriores.

Ejercicio

• Intente crear una red de solo dos capas, entrada y salida, sin ocultación, con 784 y 10 neuronas, respectivamente. Entrena la red con descenso de gradiente estocástico. ¿Qué precisión de clasificación obtienes?

Anteriormente omití los detalles de cargar datos de MNIST. Sucede de manera bastante simple. Aquí está el código para completar la imagen. Las estructuras de datos se describen en los comentarios: todo es simple, tuplas y matrices de objetos Numpy ndarray (si no está familiarizado con dichos objetos, imagínelos como vectores).

 """ mnist_loader ~~~~~~~~~~~~      MNIST.       ``load_data``  ``load_data_wrapper``.  , ``load_data_wrapper`` -  ,     . """ ####  #  import cPickle import gzip #  import numpy as np def load_data(): """  MNIST   ,  ,    . ``training_data``      .    .  numpy ndarray  50 000 .   –     numpy ndarray  784 ,  28 * 28 = 784    MNIST.  –  numpy ndarray  50 000 .   –   0  9   ,    . ``validation_data``  ``test_data`` ,    10 000 .    ,           ``training_data``.    - ``load_data_wrapper()``. """ f = gzip.open('../data/mnist.pkl.gz', 'rb') training_data, validation_data, test_data = cPickle.load(f) f.close() return (training_data, validation_data, test_data) def load_data_wrapper(): """ ,  ``(training_data, validation_data, test_data)``.   ``load_data``,         .  , ``training_data`` -    50 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   . ``y`` -  10- numpy.ndarray,   ,     ``x``. ``validation_data``  ``test_data`` -  ,   10 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   ,  ``y`` -   ,  ,   ( ),  ``x``. ,  ,           .         .""" tr_d, va_d, te_d = load_data() training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]] training_results = [vectorized_result(y) for y in tr_d[1]] training_data = zip(training_inputs, training_results) validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]] validation_data = zip(validation_inputs, va_d[1]) test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]] test_data = zip(test_inputs, te_d[1]) return (training_data, validation_data, test_data) def vectorized_result(j): """ 10-    1.0   j     .      (0..9)     .""" e = np.zeros((10, 1)) e[j] = 1.0 return e 

Dije que nuestro programa está logrando resultados bastante buenos. ¿Qué significa esto? ¿Bueno comparado con qué? Es útil tener los resultados de algunas pruebas simples y básicas con las que podría hacer una comparación para comprender qué significan "buenos resultados". El nivel base más simple, por supuesto, sería una suposición aleatoria. Esto se puede hacer en aproximadamente el 10% de los casos. ¡Y mostramos un resultado mucho mejor!

¿Qué pasa con un nivel base menos trivial? Veamos qué tan oscura es la imagen. Por ejemplo, la imagen 2 generalmente será más oscura que la imagen 1, simplemente porque tiene más píxeles oscuros, como se ve en los ejemplos a continuación:



De ello se deduce que podemos calcular la oscuridad promedio para cada dígito de 0 a 9. Cuando obtenemos una nueva imagen, calculamos su oscuridad y suponemos que muestra una figura con la oscuridad promedio más cercana. Este es un procedimiento simple que es fácil de programar, por lo que no escribiré código; si está interesado, se encuentra en GitHub . Pero esta es una mejora seria en comparación con las suposiciones aleatorias: el código reconoce correctamente 2,225 de 10,000 imágenes, es decir, proporciona una precisión del 22.25%.

No es difícil encontrar otras ideas que logren precisión en el rango de 20 a 50%. Después de trabajar un poco más, puede superar el 50%. Pero para lograr una precisión mucho mayor, es mejor usar algoritmos MO autoritativos. Probemos con uno de los algoritmos más famosos, el método de vector de soporte o SVM. Si no está familiarizado con SVM, no se preocupe, no necesitamos comprender estos detalles. Solo usamos una biblioteca de Python llamada scikit-learn, que proporciona una interfaz simple a la biblioteca rápida de C para SVM, conocida como LIBSVM .

Si ejecutamos el clasificador SVM scikit-learn con la configuración predeterminada, obtenemos la clasificación correcta de 9,435 de 10,000 (el código está disponible en el enlace) Esto ya es una gran mejora sobre el enfoque ingenuo de clasificar imágenes por oscuridad. Esto significa que SVM funciona tan bien como nuestro NS, solo que un poco peor. En los siguientes capítulos nos familiarizaremos con nuevas técnicas que nos permitirán mejorar nuestro NS para que superen en gran medida a SVM.

Pero eso no es todo.El resultado 9 435 de 10 000 de scikit-learn se especifica para la configuración predeterminada. SVM tiene muchos parámetros que se pueden ajustar, y puede buscar parámetros que mejoren este resultado. No entraré en detalles; se pueden leer en el artículo de Andreas Muller. Mostró que al hacer un trabajo para optimizar los parámetros, es posible lograr una precisión de al menos 98.5%. En otras palabras, un SVM bien sintonizado genera solo un dígito de 70 errores. ¡Un buen resultado! ¿Puede NA lograr más?

Resulta que pueden. Hoy, un NS bien ajustado supera cualquier otra tecnología conocida en la solución MNIST, incluida SVM. Récord para 2013clasificó correctamente 9,979 de 10,000 imágenes. Y veremos la mayoría de las tecnologías utilizadas para esto en este libro. Este nivel de precisión es cercano al humano, y tal vez incluso lo supera, ya que varias imágenes de MNIST son difíciles de descifrar incluso para humanos, por ejemplo:



¡Creo que estará de acuerdo en que es difícil clasificarlas! Con tales imágenes en el conjunto de datos MNIST, es sorprendente que el NS pueda reconocer correctamente todas las 10,000 imágenes, excepto 21. Por lo general, los programadores creen que resolver una tarea tan compleja requiere un algoritmo complejo. Pero incluso el NS está en el trabajoel titular del registro utiliza algoritmos bastante simples, que son pequeñas variaciones de los que examinamos en este capítulo. Toda la complejidad aparece automáticamente durante el entrenamiento en función de los datos de entrenamiento. En cierto sentido, la moraleja de nuestros resultados y los contenidos en trabajos más complejos es que para algunas tareas

algoritmo complejo ≤ algoritmo de entrenamiento simple + buenos datos de entrenamiento

Al aprendizaje profundo

Aunque nuestra red muestra un rendimiento impresionante, se logra de una manera misteriosa. Los pesos y las redes de mezcla se detectan automáticamente. Por lo tanto, no tenemos una explicación lista de cómo la red hace lo que hace. ¿Hay alguna manera de entender los principios básicos de clasificación por una red de números escritos a mano? ¿Y es posible, dados ellos, mejorar el resultado?

Reformulamos estas preguntas de manera más estricta: supongamos que en unas pocas décadas el NS se convertirá en inteligencia artificial (IA). ¿Entenderemos cómo funciona esta IA? Quizás las redes seguirán siendo incomprensibles para nosotros, con sus pesos y compensaciones, ya que se asignan automáticamente. En los primeros años de la investigación de IA, la gente esperaba que intentar crear IA también nos ayudaría a comprender los principios subyacentes de la inteligencia, y tal vez incluso el trabajo del cerebro humano. Sin embargo, al final puede resultar que no entenderemos ni el cerebro ni cómo funciona la IA.

Para abordar estos problemas, recordemos la interpretación de las neuronas artificiales que di al comienzo del capítulo: que esta es una forma de sopesar la evidencia. Supongamos que queremos determinar si la cara de una persona está en una imagen:







Este problema puede abordarse de la misma manera que el reconocimiento de escritura a mano: el uso de píxeles de imagen como entrada para el NS, y la salida del NS será una neurona que dirá: "Sí, esta es una cara" o "No, esto no es una cara ".

Supongamos que hacemos esto, pero sin usar un algoritmo de aprendizaje. Intentaremos crear manualmente una red, eligiendo los pesos y las compensaciones apropiadas. ¿Cómo podemos abordar esto? Por un momento, olvidando la Asamblea Nacional, podríamos dividir la tarea en subtareas: ¿la imagen de los ojos tiene en la esquina superior izquierda? ¿Hay un ojo en la esquina superior derecha? ¿Hay una nariz media? ¿Hay una boca en el medio? ¿Hay pelo en la parte superior? Y así sucesivamente.

Si las respuestas a varias de estas preguntas son positivas, o incluso "probablemente sí", entonces concluimos que la imagen puede tener una cara. Por el contrario, si las respuestas son no, entonces probablemente no hay persona.

Esto, por supuesto, es una heurística aproximada y tiene muchas deficiencias. Quizás sea un hombre calvo y no tenga cabello. Quizás podamos ver solo una parte de la cara, o la cara en ángulo, de modo que algunas partes de la cara estén cerradas. Sin embargo, la heurística sugiere que si podemos resolver subproblemas con la ayuda de redes neuronales, entonces quizás podamos crear NS para reconocimiento facial combinando redes para subtareas. La siguiente es una posible arquitectura de dicha red en la que las subredes se indican mediante rectángulos. Este no es un enfoque completamente realista para resolver el problema del reconocimiento facial: es necesario para ayudarnos a comprender intuitivamente el trabajo de las redes neuronales.


En los rectángulos hay subtareas: ¿tiene la imagen de los ojos en la esquina superior izquierda? ¿Hay un ojo en la esquina superior derecha? ¿Hay una nariz media? ¿Hay una boca en el medio? ¿Hay pelo en la parte superior? Y así sucesivamente.

Es posible que las subredes también se puedan desmontar en componentes. Tome la cuestión de tener un ojo en la esquina superior izquierda. Se puede distinguir en preguntas como: "¿Hay una ceja?", "¿Hay pestañas?", "¿Hay una pupila?" Y así sucesivamente. Por supuesto, las preguntas deben contener información sobre la ubicación: "¿Está la ceja ubicada en la esquina superior izquierda, arriba de la pupila?", Y así sucesivamente, pero simplifiquemosla por ahora. Por lo tanto, la red que responde a la pregunta sobre la presencia del ojo se puede desmontar en los componentes:


"¿Hay una ceja?", "¿Hay pestañas?", "¿Hay una pupila?"

Estas preguntas se pueden dividir en pequeñas, en pasos a través de muchas capas. Como resultado, trabajaremos con subredes que respondan preguntas tan simples que puedan desmontarse fácilmente a nivel de píxeles. Estas preguntas pueden referirse, por ejemplo, a la presencia o ausencia de formas simples en ciertos lugares de la imagen. Las neuronas individuales asociadas con los píxeles podrán responder a ellas.

El resultado es una red que desglosa preguntas muy complejas, ya sea que una persona esté en la imagen, en preguntas muy simples que pueden responderse a nivel de píxel individual. Lo hará a través de una secuencia de muchas capas, en la cual las primeras responden preguntas muy simples y específicas sobre la imagen, y las últimas crean una jerarquía de conceptos más complejos y abstractos. Las redes con una estructura multicapa de este tipo, dos o más capas ocultas, se denominan redes neuronales profundas (GNS).

Por supuesto, no hablé sobre cómo hacer esta subred recursiva. Definitivamente no será práctico seleccionar manualmente pesos y compensaciones. Nos gustaría utilizar algoritmos de entrenamiento para que la red aprenda automáticamente los pesos y las compensaciones, y a través de ellos las jerarquías de conceptos, basadas en datos de entrenamiento. Los investigadores en las décadas de 1980 y 1990 intentaron utilizar el descenso de gradiente estocástico y la propagación hacia atrás para entrenar GNS. Desafortunadamente, con la excepción de algunas arquitecturas especiales, no tuvieron éxito. Las redes entrenaron, pero muy lentamente, y en la práctica fue demasiado lento para que se pueda utilizar de alguna manera.

Desde 2006, se han desarrollado varias tecnologías para entrenar STS. Se basan en el descenso de gradiente estocástico y la propagación hacia atrás, pero también contienen nuevas ideas. Permitieron entrenar redes mucho más profundas; hoy en día, las personas entrenan silenciosamente redes con 5-10 capas. Y resulta que resuelven muchos problemas mucho mejor que los NS poco profundos, es decir, las redes con una capa oculta. La razón, por supuesto, es que STS puede crear una compleja jerarquía de conceptos. Esto es similar a cómo los lenguajes de programación usan esquemas modulares e ideas de abstracción para que puedan crear programas informáticos complejos. Comparar un NS profundo con un NS superficial es aproximadamente cómo comparar un lenguaje de programación que puede realizar llamadas a funciones con un lenguaje que no lo hace. La abstracción en el NS no se parece a los lenguajes de programación,Pero tiene la misma importancia.