Que haya algún experimento abstracto en el proceso del cual pueda ocurrir un determinado evento. Este experimento se llevó a cabo cinco veces, y en cuatro de ellos tuvo lugar el mismo evento. ¿Qué conclusiones se pueden sacar de estos 4/5?

Hay
una fórmula de Bernoulli que da la respuesta con qué probabilidad 4 de 5 ocurre con una probabilidad inicial conocida. Pero ella no da una respuesta, ¿cuál fue la probabilidad inicial si los eventos resultaron ser 4 de 5. Dejemos de lado la fórmula de Bernoulli.
Hagamos un pequeño programa simple que simule los procesos de probabilidad para tal caso, y en base al resultado de los cálculos, construimos un gráfico.
void test1() { uint sz_ar_events = 50;
El código para este programa se puede encontrar
aquí , junto con funciones auxiliares.
El cálculo fue arrojado a Excel e hizo un horario.

Esta versión del gráfico puede llamarse distribución de densidad de probabilidad del valor de probabilidad. Su área es igual a la unidad que se distribuye en este montículo.
Para completar, mencionaré que este gráfico corresponde al gráfico de acuerdo con la fórmula de Bernoulli del parámetro de probabilidad y multiplicado por N + 1 número de experimentos.
Además en el texto, donde uso una fracción de la forma k / n en el artículo, esto no es una división, son k eventos de n experimentos, para no escribir k de n cada vez.
Siguiente Es posible aumentar el número de experimentos y obtener una región más estrecha de la ubicación de los valores principales del valor de probabilidad, pero no importa cómo se aumenten, esta región no se reducirá a la región cero con una probabilidad conocida.
El siguiente gráfico muestra las distribuciones para 4/5, 7/9, 11/14 y 24/30. Cuanto más angosto es el área, más alto es el montículo, cuya área es una unidad constante. Estas relaciones fueron elegidas porque son todas alrededor de 0.8, y no porque son precisamente estas las que pueden surgir a 0.8 de la probabilidad inicial. Seleccionado para demostrar qué rango de valores posibles permanece incluso con 30 experimentos realizados.
El código del programa para este gráfico está
aquí .

De lo que se deduce que en realidad la probabilidad experimental no puede determinarse exactamente, pero solo podemos suponer la región de la posible ubicación de tal cantidad, con una precisión que depende de cuántas mediciones se tomaron.
No importa cuántos experimentos se realicen, siempre existe la posibilidad de que la probabilidad inicial sea de 0.0001 y 0.9999. Por simplicidad, se descartan valores extremadamente improbables. Y tomamos, digamos, por ejemplo, el 95% del área principal del cronograma de distribución.
Tal cosa se llama intervalos de confianza. No he encontrado ninguna recomendación sobre cuánto y por qué debería dejarse el interés. Para el pronóstico del tiempo, tome menos, para lanzar más transbordadores espaciales. Por lo general, tampoco mencionan qué intervalo de confianza se utiliza para la probabilidad de eventos y si se utiliza en absoluto.
En mi programa, el cálculo de los límites del intervalo de confianza se realiza
aquí .
Resultó que la probabilidad del evento está determinada por la densidad de probabilidad del valor de probabilidad, y aún es necesario imponerle un porcentaje del área de los valores principales para que al menos pueda decir definitivamente qué tipo de probabilidad es el evento en estudio.
Ahora, sobre un experimento más real.
Deje que todos se aburran con una moneda, tire esta moneda y obtenga 4 de 5 gotas por colas, un caso muy real. De hecho, esto no es lo mismo que se describe un poco más arriba. ¿Cómo es esto diferente del experimento anterior?
El experimento anterior se describió suponiendo que la probabilidad del evento se puede distribuir equitativamente en el intervalo de 0 a 1. En el programa, esto se especifica mediante la línea
doble probabilidad = get_random_real_0_1 (); . Pero no hay monedas con probabilidad de caer, digamos, 0.1 o 0.9 siempre están en un lado.
Si toma mil monedas diferentes, desde las ordinarias hasta las más curvas, y para cada una mide la pérdida lanzándolas mil o más veces, mostrará que realmente se caen de un lado en el rango de 0.4 a 0.6 (estos son números aleatorios, no lo haré pero busco 1000 monedas y las lanzo 1000 veces).
¿Cómo cambia este hecho el programa para simular las probabilidades de una moneda en particular, para la cual se recibieron 4 de 5 colas?
Suponga que la distribución de la pérdida en un lado para las monedas se describe como una aproximación al gráfico de la distribución normal tomada con parámetros promedio = 0.5, desviación estándar = 0.1. (en el gráfico a continuación se muestra en negro).
Cuando en un programa cambio la generación de la probabilidad inicial de distribuida equitativamente a distribuida de acuerdo con la regla especificada, obtengo los siguientes gráficos:
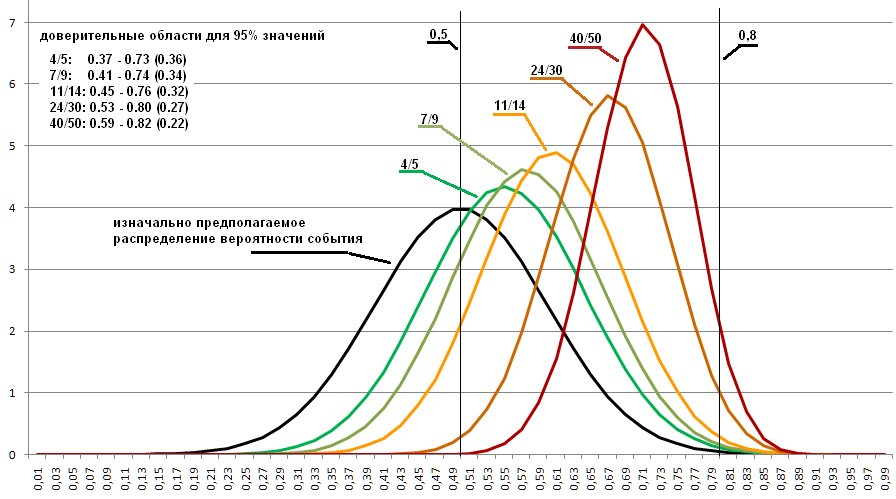
El código para esta opción está
aquí .
Se puede ver que las distribuciones han cambiado fuertemente y ahora determinan una región ligeramente diferente en la que la probabilidad deseada es altamente probable. Por lo tanto, si se sabe qué probabilidades existen para esas cosas, una de las cuales queremos medir, entonces esto puede mejorar el resultado.
Como resultado, 4/5 no significa nada, e incluso 50 de los experimentos realizados no son muy informativos. Esta es muy poca información para determinar qué tipo de probabilidad aún subyace al experimento.
== Actualización ==
Como
Jzha mencionó en los comentarios, una persona que conoce las matemáticas de manera significativa, estos gráficos también se pueden construir utilizando fórmulas exactas. Pero el propósito de este artículo sigue siendo demostrar lo más claramente posible cómo se forma lo que todos en la vida cotidiana llaman probabilidad.
Para construirlo usando fórmulas exactas, es necesario considerar los datos disponibles sobre la distribución de probabilidad de todas las monedas a través de la aproximación de la distribución beta, y al calcular las distribuciones, obtener los cálculos ya. Tal esquema es una cantidad sustancial de explicaciones sobre cómo hacer esto, y si lo describo aquí, resultará ser un artículo sobre cálculos matemáticos, en lugar de probabilidades cotidianas.
Cómo obtener las fórmulas describe un caso especial con una moneda, vea los comentarios de
jzha .