¿Cómo acelerar la descompresión de LZ4 en ClickHouse?

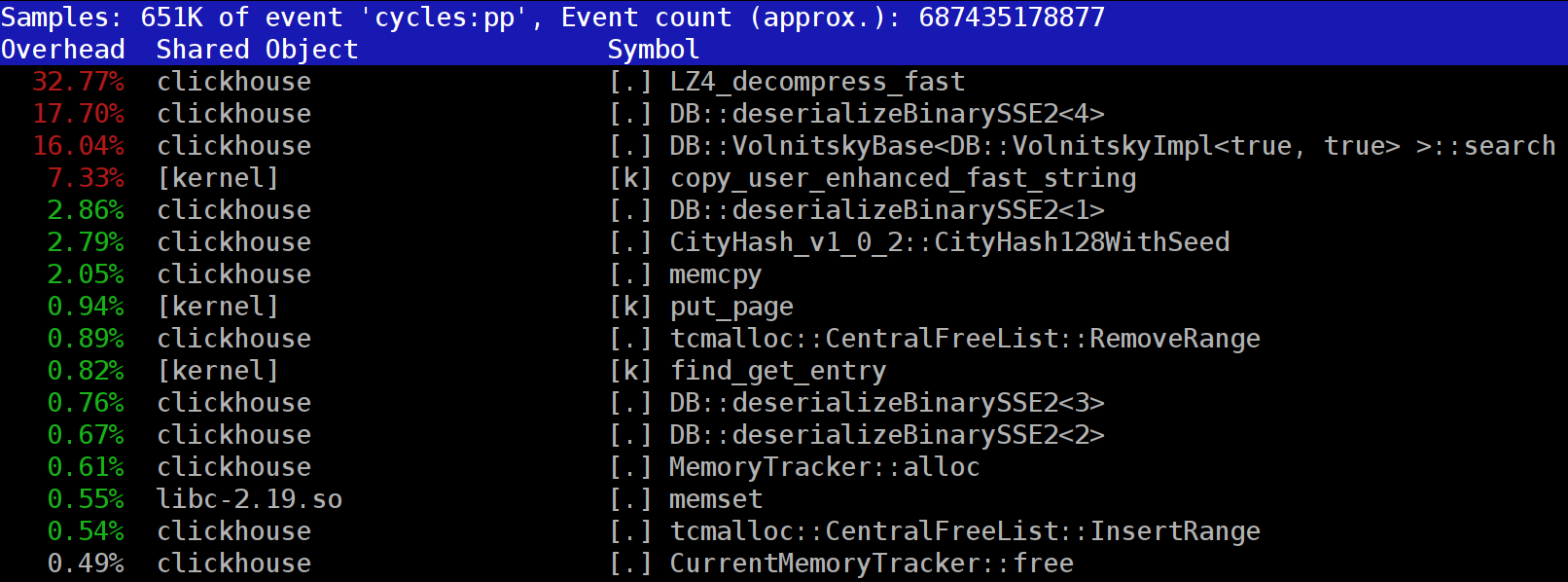
Cuando ejecuta consultas en ClickHouse , puede notar que el generador de perfiles a menudo muestra la función LZ_decompress_fast cerca de la parte superior. Que esta pasando Esta pregunta nos hizo preguntarnos cómo elegir el mejor algoritmo de compresión.

ClickHouse almacena datos en forma comprimida. Al ejecutar consultas, ClickHouse intenta hacer lo menos posible para conservar los recursos de la CPU. En muchos casos, todos los cálculos potencialmente lentos ya están bien optimizados, además el usuario escribió una consulta bien pensada. Entonces todo lo que queda por hacer es realizar la descompresión.



Entonces, ¿por qué la descompresión LZ4 se convierte en un cuello de botella? LZ4 parece un algoritmo extremadamente ligero : la tasa de descompresión de datos suele ser de 1 a 3 GB / s por núcleo de procesador, dependiendo de los datos. Esto es mucho más rápido que el subsistema de disco típico. Además, utilizamos todos los núcleos de CPU disponibles, y la descompresión se escala linealmente en todos los núcleos físicos.

Sin embargo, hay dos puntos a tener en cuenta. Primero, los datos comprimidos se leen del disco, pero la velocidad de descompresión se da en términos de la cantidad de datos sin comprimir. Si la relación de compresión es lo suficientemente grande, no hay casi nada que leer de los discos. Pero habrá muchos datos descomprimidos, y esto naturalmente afecta la utilización de la CPU: en el caso de LZ4, la cantidad de trabajo necesaria para descomprimir datos es casi proporcional al volumen de los datos descomprimidos.

En segundo lugar, si los datos se almacenan en caché, es posible que no necesite leer datos de los discos. Puede confiar en el caché de página o usar su propio caché. El almacenamiento en caché es más eficiente en bases de datos orientadas a columnas, ya que solo las columnas de uso frecuente permanecen en la memoria caché. Es por eso que LZ4 a menudo parece ser un cuello de botella en términos de carga de CPU.

Esto trae dos preguntas más. Primero, si la descompresión nos está ralentizando, ¿vale la pena comprimir los datos para empezar? Pero esta especulación es irrelevante en la práctica. Hasta hace poco, la configuración de ClickHouse ofrecía solo dos opciones de compresión de datos: LZ4 y Zstandard . LZ4 se usa por defecto. Cambiar a Zstandard hace que la compresión sea más fuerte y más lenta. Pero no había una opción para desactivar por completo la compresión, ya que se supone que LZ4 proporciona una compresión mínima razonable que siempre se puede usar. (Por eso me encanta LZ4.)

Pero luego apareció un extraño misterioso en el chat internacional de soporte de ClickHouse que dijo que tiene un subsistema de disco muy rápido (con NVMe SSD) y que la descompresión es lo único que ralentiza sus consultas, por lo que sería bueno poder almacenar datos sin compresión Respondí que no tenemos esta opción, pero sería fácil de agregar. Unos días más tarde, recibimos una solicitud de extracción implementando el método de compresión none . Le pedí al contribuyente que informara sobre cuánto esta opción ayudó a acelerar las consultas. La respuesta fue que esta nueva característica resultó inútil en la práctica, ya que los datos sin comprimir comenzaron a ocupar demasiado espacio en disco y no cabían en esas unidades NVMe.

La segunda pregunta que surge es que si hay un caché, ¿por qué no usarlo para almacenar datos que ya están descomprimidos? Esta es una posibilidad viable que eliminará la necesidad de descompresión en muchos casos. ClickHouse también tiene un caché como este: el caché de bloques descomprimidos . Pero es una pena desperdiciar mucha RAM en esto. Por lo tanto, generalmente tiene sentido usar consultas pequeñas y secuenciales que usan datos casi idénticos.

Nuestra conclusión es que siempre es preferible almacenar datos en formato comprimido. Siempre escriba datos en el disco en formato comprimido. Transmita datos a través de la red con compresión también. En mi opinión, la compresión predeterminada es justificable incluso cuando se transfieren datos dentro de un solo centro de datos en una red de 10 GB sin una suscripción excesiva, mientras que la transferencia de datos sin comprimir entre centros de datos es simplemente inaceptable.

¿Por qué LZ4?

¿Por qué elegir LZ4? ¿No podríamos elegir algo aún más ligero? Teóricamente, podríamos, y este es un buen pensamiento. Pero veamos la clase de algoritmos a los que pertenece LZ4.

En primer lugar, es genérico y no adapta el tipo de datos. Por ejemplo, si sabe de antemano que tendrá una serie de enteros, puede usar uno de los algoritmos VarInt y esto usará la CPU de manera más efectiva. En segundo lugar, LZ4 no depende demasiado de los supuestos del modelo de datos. Supongamos que tiene una serie temporal ordenada de valores de sensores, una matriz de números de punto flotante. Si tiene esto en cuenta, puede calcular deltas entre estos números y luego comprimirlos con un algoritmo genérico, lo que dará como resultado una relación de compresión más alta.

No tendrá ningún problema al usar LZ4 con cualquier conjunto de bytes o cualquier archivo. Por supuesto, tiene una especialización (más sobre eso más adelante), y en algunos casos su uso no tiene sentido. Pero si lo llamamos un algoritmo de propósito general, estaremos bastante cerca de la verdad. Debemos tener en cuenta que gracias a su diseño interno, LZ4 implementa automáticamente el algoritmo RLE como un caso especial.

Sin embargo, la pregunta más importante es si LZ4 es el algoritmo más óptimo de esta clase en términos de velocidad general y fuerza de compresión. Los algoritmos óptimos se denominan frontera de Pareto, lo que significa que no hay otro algoritmo que sea definitivamente mejor de una manera y no peor de otras (y también en una amplia variedad de conjuntos de datos). Algunos algoritmos son más rápidos pero dan como resultado una relación de compresión más pequeña, mientras que otros tienen una compresión más fuerte pero son más lentos para comprimir o descomprimir.

Para ser sincero, LZ4 no es realmente la frontera de Pareto: hay algunas opciones disponibles que son solo un poco mejores. Por ejemplo, mire LZTURBO de un desarrollador apodado powturbo . No hay dudas sobre la fiabilidad de los resultados, gracias a la comunidad encode.ru (el foro más grande y posiblemente el único sobre compresión de datos). Desafortunadamente, el desarrollador no distribuye el código fuente o los binarios; solo están disponibles para un número limitado de personas para la prueba, o por una gran cantidad de dinero (aunque parece que todavía nadie lo ha pagado). También eche un vistazo a Lizard (anteriormente LZ5) y Density . Pueden funcionar un poco mejor que LZ4 cuando selecciona un cierto nivel de compresión. Otra opción realmente interesante es LZSSE . Pero termine de leer este artículo antes de echarle un vistazo.

Como funciona lz4

Veamos cómo funciona LZ4 en general. Esta es una de las implementaciones del algoritmo LZ77. L y Z representan los nombres de los desarrolladores (Lempel y Ziv), y 77 es para el año 1977 cuando se publicó el algoritmo. Tiene muchas otras implementaciones: QuickLZ, FastLZ, BriefLZ, LZF, LZO y gzip y zip si se utilizan niveles bajos de compresión.

Un bloque de datos comprimido usando LZ4 contiene una secuencia de entradas (comandos o instrucciones) de dos tipos:

1. Literales: "Tome los siguientes N bytes tal cual y cópielos en el resultado".
2. Coincidencia: "Tomar N bytes del resultado descomprimido comenzando en el valor de desplazamiento relativo a la posición actual".

Ejemplo. Antes de la compresión:

 Hello world Hello 

Después de la compresión:

 literals 12 "Hello world " match 5 12 

Si tomamos un bloque comprimido e iteramos el cursor a través de él mientras ejecutamos estos comandos, obtendremos los datos originales sin comprimir como resultado.

Así es básicamente cómo se descomprimen los datos. La idea básica es clara: para realizar la compresión, el algoritmo codifica una secuencia repetida de bytes usando coincidencias.

Algunas características también son claras. Este algoritmo orientado a bytes no disecciona bytes individuales; solo los copia en su totalidad. Así es como difiere de la codificación de entropía. Por ejemplo, zstd es una combinación de LZ77 y codificación de entropía.

Tenga en cuenta que el tamaño del bloque comprimido no debe ser demasiado grande. El tamaño se elige para evitar el desperdicio de una gran cantidad de RAM durante la descompresión, para evitar ralentizar demasiado el acceso aleatorio en el archivo comprimido (que consiste en una gran cantidad de bloques comprimidos) y, a veces, el bloque cabe en un caché de la CPU. Por ejemplo, puede elegir 64 KB para que los búferes para datos comprimidos y sin comprimir quepan en la caché L2 con la mitad aún libre.

Si necesitamos comprimir un archivo más grande, podemos concatenar los bloques comprimidos. Esto también es conveniente para almacenar datos adicionales (como una suma de verificación) con cada bloque comprimido.

El desplazamiento máximo para el partido es limitado. En LZ4, el límite es de 64 kilobytes. Esta cantidad se llama ventana deslizante. Esto significa que las coincidencias se pueden encontrar en una ventana de 64 kilobytes que precede al cursor, que se desliza con el cursor a medida que avanza.

Ahora veamos cómo comprimir datos o, en otras palabras, cómo encontrar secuencias coincidentes en un archivo. Siempre puedes usar un sufijo trie (es genial si realmente has oído hablar de esto). Hay métodos que garantizan que la coincidencia más larga se encuentra en los bytes anteriores después de la compresión. Esto se llama análisis óptimo y proporciona casi la mejor relación de compresión para un bloque comprimido de formato fijo. Pero hay mejores enfoques, como encontrar una coincidencia lo suficientemente buena que no sea necesariamente la más larga. La forma más eficiente de encontrarlo es usando una tabla hash.

Para hacer esto, iteramos el cursor a través del bloque de datos original y tomamos algunos bytes después del cursor (digamos 4 bytes). Los hash y colocamos el desplazamiento desde el principio del bloque (de donde se tomaron los 4 bytes) en la tabla hash. El valor 4 se llama "min-match": con esta tabla hash, podemos encontrar coincidencias de al menos 4 bytes.

Si miramos la tabla hash y ya tiene un registro coincidente, y el desplazamiento no excede la ventana deslizante, verificamos cuántos bytes más coinciden después de esos 4 bytes. Quizás haya muchos más partidos. También es posible que haya una colisión en la tabla hash y que nada coincida, pero esto no es gran cosa. Simplemente puede reemplazar el valor en la tabla hash con uno nuevo. Las colisiones en la tabla hash simplemente conducirán a una relación de compresión más baja, ya que habrá menos coincidencias. Por cierto, este tipo de tabla hash (con un tamaño fijo y sin resolución de colisiones) se denomina "tabla de caché". Este nombre tiene sentido porque en caso de colisión, la tabla de caché simplemente olvida la entrada anterior.

Un desafío para el lector cuidadoso. Supongamos que los datos son una matriz de números UInt32 en formato little endian que representa una parte de una secuencia de números naturales: 0, 1, 2 ... Explique por qué estos datos no se comprimen cuando se usa LZ4 (el tamaño de los datos comprimidos no es más pequeño en comparación con los datos sin comprimir).

Cómo acelerar todo

Entonces quiero acelerar la descompresión de LZ4. Veamos cómo se ve el ciclo de descompresión. Aquí está en pseudocódigo:

 while (...) {    read(input_pos, literal_length, match_length);    copy(output_pos, input_pos, literal_length);    output_pos += literal_length;    read(input_pos, match_offset);    copy(output_pos, output_pos - match_offset,        match_length);    output_pos += match_length; } 

El formato LZ4 está diseñado para que los literales y las coincidencias se alternen en un archivo comprimido. Obviamente, el literal siempre viene primero (porque no hay un lugar desde el que comenzar una partida desde el principio). Por lo tanto, sus longitudes están codificadas juntas.

En realidad es un poco más complicado que eso. Se lee un byte del archivo, y luego se divide en dos nibbles (medios bytes) que contienen los números codificados del 0 al 15. Si el número correspondiente no es 15, se supone que es la longitud del literal y la coincidencia, respectivamente. Y si es 15, la longitud es mayor y está codificada en los siguientes bytes. Luego se lee el siguiente byte y su valor se agrega a la longitud. Si es igual a 255, se hace lo mismo con el siguiente byte.

Tenga en cuenta que la relación de compresión máxima para el formato LZ4 no alcanza 255. Y otra observación inútil es que si sus datos son muy redundantes, usar LZ4 dos veces mejorará la relación de compresión.

Cuando leemos la longitud de un literal (y luego la longitud de la coincidencia y el desplazamiento de la coincidencia), basta con copiar dos bloques de memoria para descomprimirlo.

Cómo copiar un bloque de memoria

Parece que podría usar la función memcpy , que está diseñada para copiar bloques de memoria. Pero este no es el enfoque óptimo y no es realmente apropiado.

Usar memcpy no es óptimo porque:

1. Por lo general, se encuentra en la biblioteca libc (y la biblioteca libc generalmente está vinculada dinámicamente, por lo que la llamada a memcpy se realizará indirectamente a través de PLT).
2. El compilador no lo alinea si el argumento de tamaño es desconocido en el momento de la compilación.
3. Hace un gran esfuerzo para procesar correctamente las sobras de un bloque de memoria que no son múltiplos de la longitud de la máquina o el registro.

El último punto es el más importante. Digamos que le pedimos a la función memcpy que copie exactamente 5 bytes. Sería genial copiar 8 bytes de inmediato, utilizando dos instrucciones movq.

Hello world Hello wo ...
^^^^^ ^^^ - src
^^^^^ ^^^ - dst

Pero luego copiaremos tres bytes adicionales, por lo que escribiremos fuera de los límites del búfer. La función memcpy no tiene permiso para hacer esto, ya que podría sobrescribir algunos datos en nuestro programa y provocar un error de memoria. Y si escribimos a una dirección no alineada, estos bytes adicionales podrían aterrizar en una página no asignada de memoria virtual o en una página sin acceso de escritura. Eso nos daría una falla de segmentación (esto es bueno).

Pero en nuestro caso, casi siempre podemos escribir bytes adicionales. Podemos leer bytes adicionales en el búfer de entrada siempre que los bytes adicionales se encuentren completamente dentro de él. En las mismas condiciones, podemos escribir los bytes adicionales en el búfer de salida, porque aún los sobrescribiremos en la próxima iteración.

Esta optimización ya está en la implementación original de LZ4:

 inline void copy8(UInt8 * dst, const UInt8 * src) {    memcpy(dst, src, 8); /// Note that memcpy isn't actually called here. } inline void wildCopy8(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) {    do    {        copy8(dst, src);        dst += 8;        src += 8;    } while (dst < dst_end); } 

Para aprovechar esta optimización, solo debemos asegurarnos de que estamos lo suficientemente lejos de los límites del búfer. Esto no debería costar nada, porque ya estamos comprobando el desbordamiento del búfer. Y el procesamiento de los últimos bytes, los datos "sobrantes", se puede hacer después del bucle principal.

Sin embargo, todavía hay algunos matices. La copia se produce dos veces en el ciclo: con un literal y una coincidencia. Sin embargo, cuando se usa la función LZ4_decompress_fast (en lugar de LZ4_decompress_safe ), la verificación se realiza solo una vez, cuando necesitamos copiar el literal. La verificación no se realiza al copiar la coincidencia, pero la especificación para el formato LZ4 tiene condiciones que le permiten evitarlo:

Los últimos 5 bytes son siempre literales.
La última coincidencia debe comenzar al menos 12 bytes antes del final del bloque.
En consecuencia, un bloque con menos de 13 bytes no se puede comprimir.

Los datos de entrada especialmente seleccionados pueden provocar daños en la memoria. Si utiliza la función LZ4_decompress_fast , necesita protección contra datos incorrectos. Como mínimo, debe calcular sumas de verificación para los datos comprimidos. Si necesita protección contra hackers, use la función LZ4_decompress_safe . Otras opciones: tomar una función hash criptográfica como suma de comprobación (aunque es probable que esto destruya el rendimiento); asignar más memoria para buffers; asigne memoria para buffers con una llamada mmap separada y cree una página de protección.

Cuando veo un código que copia 8 bytes de datos, inmediatamente me pregunto por qué exactamente 8 bytes. Puede copiar 16 bytes utilizando registros SSE:

 inline void copy16(UInt8 * dst, const UInt8 * src) { #if __SSE2__    _mm_storeu_si128(reinterpret_cast<__m128i *>(dst),        _mm_loadu_si128(reinterpret_cast<const __m128i *>(src))); #else    memcpy(dst, src, 16); #endif } inline void wildCopy16(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) {    do    {        copy16(dst, src);        dst += 16;        src += 16;    } while (dst < dst_end); } 

Lo mismo funciona para copiar 32 bytes para AVX y 64 bytes para AVX-512. Además, puede desenrollar el bucle varias veces. Si alguna vez ha visto cómo se implementa memcpy , este es exactamente el enfoque que se utiliza. (Por cierto, el compilador no desenrollará ni vectorizará el bucle en este caso, porque esto requerirá la inserción de comprobaciones voluminosas).

¿Por qué la implementación original de LZ4 no hizo esto? Primero, no está claro si esto es mejor o peor. La ganancia resultante depende del tamaño de los bloques a copiar, por lo que si todos son cortos, crearía trabajo extra para nada. Y en segundo lugar, arruina las disposiciones en el formato LZ4 que ayudan a evitar una rama innecesaria en el bucle interno.

Sin embargo, tendremos en cuenta esta opción por el momento.

Copia difícil

Volvamos a la pregunta de si siempre es posible copiar datos de esta manera. Digamos que necesitamos copiar una coincidencia, es decir, tomar un trozo de memoria del búfer de salida que se encuentra en algún desplazamiento detrás del cursor y copiarlo en la posición del cursor.

Imagine un caso simple cuando necesita copiar 5 bytes en un desplazamiento de 12:

Hello world ...........
^^^^^ - src
^^^^^ - dst

Hello world Hello wo ...
^^^^^ - src
^^^^^ - dst

Pero hay un caso más difícil, cuando necesitamos copiar un bloque de memoria que es más largo que el desplazamiento. En otras palabras, incluye algunos datos que aún no se han escrito en el búfer de salida.

Copie 10 bytes con un desplazamiento de 3:

abc .............
^^^^^^^^^^ - src
^^^^^^^^^^ - dst

abc abcabcabca ...
^^^^^^^^^^ - src
^^^^^^^^^^ - dst

Tenemos todos los datos durante el proceso de compresión, y tal coincidencia bien se puede encontrar. La función memcpy no es adecuada para copiarla, ya que no admite el caso cuando se superponen rangos de bloques de memoria. La función memmove tampoco funcionará, porque el bloque de memoria del que deben tomarse los datos aún no se ha inicializado por completo. Necesitamos copiar de la misma manera que si estuviéramos copiando byte a byte.

 op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; ... 

Así es como funciona:

a bc a ............
^ - src
^ - dst

a b ca b ...........
^ - src
^ - dst

ab c ab c ..........
^ - src
^ - dst

abc a bc a .........
^ - src
^ - dst

abca b ca b ........
^ - src
^ - dst

En otras palabras, debemos crear una secuencia repetitiva. La implementación original de LZ4 utilizó un código sorprendentemente extraño para hacer esto:

 const unsigned dec32table[] = {0, 1, 2, 1, 4, 4, 4, 4}; const int dec64table[] = {0, 0, 0, -1, 0, 1, 2, 3}; const int dec64 = dec64table[offset]; op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; match += dec32table[offset]; memcpy(op+4, match, 4); match -= dec64; 

Copia los primeros 4 bytes uno por uno, salta por delante con algún número mágico, copia los siguientes 4 bytes por completo y mueve el cursor a una coincidencia utilizando otro número mágico. El autor del código ( Yan Collet ) de alguna manera se olvidó de dejar un comentario sobre lo que esto significa. Además, los nombres de las variables son confusos. Ambos se denominan dec ... table, pero uno se agrega y el otro se resta. Además, uno de ellos no está firmado y el otro es int. Sin embargo, el autor recientemente mejoró este lugar en el código.

Así es como funciona realmente. Copiamos los primeros 4 bytes uno a la vez:

abc abca .........
^^^^ - src
^^^^ - dst

Ahora podemos copiar 4 bytes a la vez:

abcabca bcab .....
^^^^ - src
^^^^ - dst

Podemos continuar como de costumbre, copiando 8 bytes a la vez:

abcabcabcab cabcabca .....
^^^^^^^^ - src
^^^^^^^^ - dst

Como todos sabemos por experiencia, a veces la mejor manera de entender el código es reescribirlo. Esto es lo que se nos ocurrió:

 inline void copyOverlap8(UInt8 * op, const UInt8 *& match, const size_t offset) {    /// 4 % n.    /// Or if 4 % n is zero, we use n.    /// It gives an equivalent result, but is more CPU friendly for unknown reasons.    static constexpr int shift1[] = { 0, 1, 2, 1, 4, 4, 4, 4 };    /// 8 % n - 4 % n    static constexpr int shift2[] = { 0, 0, 0, 1, 0, -1, -2, -3 };    op[0] = match[0];    op[1] = match[1];    op[2] = match[2];    op[3] = match[3];    match += shift1[offset];    memcpy(op + 4, match, 4);    match += shift2[offset]; } 

Como se esperaba, esto no cambia el rendimiento en absoluto. Solo quería probar la optimización para copiar 16 bytes a la vez.

Sin embargo, esto complica el "caso especial" y hace que se llame con más frecuencia (la condición de offset < 16 se realiza al menos tan a menudo como el offset < 8 ). La copia de rangos superpuestos con copia de 16 bytes se ve así (solo se muestra el principio):

 inline void copyOverlap16(UInt8 * op, const UInt8 *& match, const size_t offset) {    /// 4 % n.    static constexpr int shift1[]        = { 0, 1, 2, 1, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4 };    /// 8 % n - 4 % n    static constexpr int shift2[]        = { 0, 0, 0, 1, 0, -1, -2, -3, -4, 4, 4, 4, 4, 4, 4, 4 };    /// 16 % n - 8 % n    static constexpr int shift3[]        = { 0, 0, 0, -1, 0, -2, 2, 1, 8, -1, -2, -3, -4, -5, -6, -7 };    op[0] = match[0];    op[1] = match[1];    op[2] = match[2];    op[3] = match[3];    match += shift1[offset];    memcpy(op + 4, match, 4);    match += shift2[offset];    memcpy(op + 8, match, 8);    match += shift3[offset]; } 

¿Se puede implementar esta función de manera más efectiva? Nos gustaría encontrar una instrucción SIMD mágica para un código tan complejo, porque todo lo que queremos hacer es escribir 16 bytes, que consisten completamente en unos pocos bytes de datos de entrada (del 1 al 15). Entonces solo necesitan repetirse en el orden correcto.

Hay una instrucción como esta llamada pshufb (bytes aleatorios empaquetados) que forma parte de SSSE3 (tres S). Acepta dos registros de 16 bytes. Uno de los registros contiene los datos de origen. El otro tiene el "selector": cada byte contiene un número del 0 al 15, según el byte del registro fuente del que tomar el resultado. Si el valor de byte del selector es mayor que 127, el byte correspondiente del resultado se llena con cero.

Aquí hay un ejemplo:

  xmm0: abc .............
 xmm1: 0120120120120120

 pshufb% xmm1,% xmm0

 xmm0: abcabcabcabcabca 

Cada byte del resultado se llena con el byte seleccionado de los datos de origen: ¡esto es exactamente lo que necesitamos! Así es como se ve el código en el resultado:

 inline void copyOverlap16Shuffle(UInt8 * op, const UInt8 *& match, const size_t offset) { #ifdef __SSSE3__    static constexpr UInt8 __attribute__((__aligned__(16))) masks[] =    {        0, 1, 2, 1, 4, 1, 4, 2, 8, 7, 6, 5, 4, 3, 2, 1, /* offset = 0, not used as mask, but for shift amount instead */        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, /* offset = 1 */        0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1,        0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0,        0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3,        0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0,        0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3,        0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1,        0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7,        0, 1, 2, 3, 4, 5, 6, 7, 8, 0, 1, 2, 3, 4, 5, 6,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 0, 1, 2,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 0, 1,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 0,    };    _mm_storeu_si128(reinterpret_cast<__m128i *>(op),        _mm_shuffle_epi8(            _mm_loadu_si128(reinterpret_cast<const __m128i *>(match)),            _mm_load_si128(reinterpret_cast<const __m128i *>(masks) + offset)));    match += masks[offset]; #else    copyOverlap16(op, match, offset); #endif } 

Aquí _mm_shuffle_epi8 es un intrínseco , que compila las instrucciones de la CPU pshufb .

¿Podemos realizar esta operación para más bytes a la vez usando instrucciones más recientes? Después de todo, SSSE3 es un conjunto de instrucciones muy antiguo que existe desde 2006. AVX2 tiene una instrucción que hace esto por 32 bytes a la vez, pero por separado para carriles individuales de 16 bytes. Esto se llama bytes de permuta de vectores, en lugar de bytes aleatorios empaquetados: las palabras son diferentes, pero el significado es el mismo. AVX-512 VBMI tiene otra instrucción que funciona para 64 bytes a la vez, pero los procesadores que lo admiten solo han aparecido recientemente. ARM NEON tiene instrucciones similares llamadas vtbl (búsqueda de tabla de vectores), pero solo permiten escribir 8 bytes.

Además, hay una versión de la instrucción pshufb con registros MMX de 64 bits para formar 8 bytes. Es justo para reemplazar la versión original del código. Sin embargo, decidí usar la opción de 16 bytes en su lugar (por razones serias).

En la conferencia Highload ++ Siberia, un asistente se me acercó después de mi presentación y mencionó que para el caso de 8 bytes, solo puede usar la multiplicación por una constante especialmente seleccionada (también necesitará un desplazamiento), esto ni siquiera había ocurrido a mi antes!

Cómo eliminar una declaración if superflua

Digamos que quiero usar una variante que copia 16 bytes. ¿Cómo puedo evitar tener que hacer una verificación adicional para el desbordamiento del búfer?

Decidí que simplemente no haría esta verificación. Los comentarios sobre la función dirán que el desarrollador debe asignar un bloque de memoria para un número específico de bytes más de lo necesario, para que podamos leer y escribir basura innecesaria allí. La interfaz de la función será más difícil de usar, pero este es un problema diferente.

En realidad, podría haber consecuencias negativas. Digamos que los datos que necesitamos descomprimir se formaron a partir de bloques de 65.536 bytes cada uno. Luego, el usuario nos da un trozo de memoria de 65,536 bytes para los datos descomprimidos. Pero con la nueva interfaz de función, el usuario deberá asignar un bloque de memoria de 65.551 bytes, por ejemplo. Entonces, el asignador puede verse obligado a asignar 96 o incluso 128 kilobytes, dependiendo de su implementación. Si el asignador es muy malo, podría detener repentinamente el almacenamiento en memoria caché en "montón" y comenzar a usar mmap y munmap cada vez para la asignación de memoria (o liberar memoria usando madvice ). Este proceso será extremadamente lento debido a fallas en la página. Como resultado, esta pequeña optimización podría terminar ralentizando todo.

¿Hay alguna aceleración?

Entonces hice una versión del código que usa tres optimizaciones:

1. Copiando 16 bytes en lugar de 8.
2. Usando las instrucciones de reproducción aleatoria para el caso offset < 16 .
3. Eliminado un extra si.

Comencé a probar este código en diferentes conjuntos de datos y obtuve resultados inesperados.

Ejemplo 1:
Xeon E2650v2, datos del navegador Yandex, columna AppVersion.
Referencia: 1,67 GB / seg.
16 bytes, aleatorio: 2.94 GB / seg (76% más rápido).

Ejemplo 2
Xeon E2650v2, datos Yandex Direct, columna ShowsSumPosition.
Referencia: 2,30 GB / seg.
16 bytes, aleatorio: 1.91 GB / seg (20% más lento).

Al principio estaba muy feliz, cuando vi que todo se había acelerado en un porcentaje tan grande. Entonces vi que nada era más rápido con otros archivos. Incluso fue un poco más lento para algunos de ellos. Llegué a la conclusión de que los resultados dependen de la relación de compresión. Cuanto más comprimido esté el archivo, mayor será la ventaja de cambiar a 16 bytes. Esto se siente natural: cuanto mayor es la relación de compresión, mayor es la longitud promedio de los fragmentos para copiar.

Para investigar, utilicé plantillas de C ++ para hacer opciones de código para cuatro casos: usando fragmentos de 8 bytes o 16 bytes, y con o sin la instrucción aleatoria.

 template <size_t copy_amount, bool use_shuffle> void NO_INLINE decompressImpl(    const char * const source,    char * const dest,    size_t dest_size) 

Las variantes completamente diferentes del código funcionaron mejor en diferentes archivos, pero cuando se prueba en un escritorio, la versión con barajado siempre ganaba. Probar en un escritorio es inconveniente porque tienes que hacer esto:

 sudo echo 'performance' | tee /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor kill -STOP $(pidof firefox) $(pidof chromium) 

Luego fui a uno de los viejos servidores de "desarrollo" (con el procesador Xeon E5645), tomé aún más conjuntos de datos y obtuve resultados casi opuestos, lo que me confundió por completo. Resulta que la elección del algoritmo óptimo depende del modelo del procesador, además de la relación de compresión. El procesador determina cuándo es mejor usar la instrucción aleatoria, así como el umbral de cuándo comenzar a usar la copia de 16 bytes.

Por cierto, al realizar pruebas en nuestros servidores, tiene sentido hacer esto:

 sudo kill -STOP $(pidof python) $(pidof perl) $(pgrep -u skynet) $(pidof cqudp-client) 

De lo contrario, los resultados serán inestables. También ten cuidado con la regulación térmica y la limitación de potencia.

Cómo elegir el mejor algoritmo

Entonces tenemos cuatro variantes del algoritmo y necesitamos elegir la mejor para las condiciones. Podríamos crear un conjunto representativo de datos y hardware, luego realizar pruebas de carga serias y elegir el método que sea mejor en promedio. Pero no tenemos un conjunto de datos representativo. Para las pruebas, utilicé una muestra de datos de Yandex Metrica , Yandex Direct, Yandex Browser y vuelos en los Estados Unidos . Pero esto no es suficiente, porque ClickHouse es utilizado por cientos de empresas en todo el mundo. Al optimizar en exceso en un conjunto de datos, podríamos causar una caída en el rendimiento con otros datos y ni siquiera darnos cuenta. Y si los resultados dependen del modelo del procesador, tendremos que escribir explícitamente las condiciones en el código y probarlo en cada modelo (o consultar el manual de referencia sobre las instrucciones de temporización, ¿qué te parece?). En cualquier caso, esto lleva demasiado tiempo.

Así que decidí usar otro método, que es obvio para los colegas que estudiaron en nuestra Escuela de Análisis de Datos: "bandidos multi-armados" . El punto es que la variante del algoritmo se elige al azar, y luego usamos estadísticas para elegir progresivamente más a menudo las opciones que funcionan mejor.

Tenemos muchos bloques de datos que deben descomprimirse, por lo que necesitamos llamadas a funciones independientes para descomprimir datos. Podríamos elegir uno de los cuatro algoritmos para cada bloque y medir su tiempo de ejecución. Una operación como esta generalmente no cuesta nada en comparación con el procesamiento de un bloque de datos, y en ClickHouse un bloque de datos sin comprimir es de al menos 64 KB. (Lea este artículo sobre la medición del tiempo).

Para comprender mejor cómo funciona el algoritmo de "bandidos multi-armados", veamos de dónde viene el nombre. Esta es una analogía con las máquinas tragamonedas en un casino que tienen varias palancas que un jugador puede tirar para obtener una cantidad aleatoria de dinero. El jugador puede tirar de las palancas varias veces en cualquier orden. Cada palanca tiene una probabilidad fija de la cantidad correspondiente de dinero entregada, pero el jugador no sabe cómo funciona y solo puede aprenderlo por experiencia en el juego. Una vez que se dan cuenta, pueden maximizar sus ganancias.

Un enfoque para maximizar la recompensa es evaluar la distribución de probabilidad para cada palanca en cada paso en función de las estadísticas del juego de los pasos anteriores. Luego, mentalmente "ganamos" una recompensa aleatoria por cada palanca, según las distribuciones recibidas. Finalmente, tiramos de la palanca que tuvo el mejor resultado en nuestro juego mental. Este enfoque se llama Thompson Sampling.

Pero estamos eligiendo un algoritmo de descompresión. El resultado es el tiempo de ejecución en picosegundos por byte: cuanto menos, mejor. Consideraremos que el tiempo de ejecución es una variable aleatoria y evaluaremos su distribución utilizando estadísticas matemáticas. El enfoque bayesiano a menudo se usa para tareas como esta, pero sería engorroso insertar fórmulas complejas en el código C ++. Podemos usar un enfoque paramétrico y decir que una variable aleatoria pertenece a una familia paramétrica de variables aleatorias, y luego evaluar sus parámetros.

¿Cómo seleccionamos la familia de variables aleatorias? Como ejemplo, podríamos suponer que el tiempo de ejecución del código tiene una distribución normal. Pero esto está absolutamente mal. Primero, el tiempo de ejecución no puede ser negativo, y la distribución normal toma valores en todas partes en la recta numérica. En segundo lugar, supongo que el tiempo de ejecución tendrá una "cola" pesada en el extremo derecho.

Sin embargo, hay factores que podrían hacer que sea una buena idea estimar la distribución normal solo para los propósitos de Thompson Sampling (a pesar de que la distribución de la variable objetivo no es necesariamente normal). La razón de esto es que es muy fácil calcular la expectativa matemática y la varianza, y después de un número suficiente de iteraciones, una distribución normal se vuelve bastante estrecha, no muy diferente de las distribuciones que habríamos obtenido usando otros métodos. Si no nos preocupamos demasiado por la tasa de convergencia en los primeros pasos, estos detalles pueden ignorarse.

Esto puede parecer un enfoque algo ignorante. La experiencia nos ha demostrado que el tiempo promedio para la ejecución de la consulta, la carga de la página del sitio web, etc. es "basura" que no vale la pena calcular. Sería mejor calcular la mediana, que es una estadística robusta . Pero esto es un poco más difícil y, como mostraré más adelante, el método descrito se justifica por razones prácticas.

Al principio implementé el cálculo de la expectativa matemática y la varianza, pero luego decidí que esto es demasiado bueno y que necesito simplificar el código para hacerlo "peor":

 /// For better convergence, we don't use proper estimate of stddev. /// We want to eventually separate the two algorithms even in cases /// when there is no statistical significant difference between them. double sigma() const {    return mean() / sqrt(adjustedCount()); } double sample(pcg64 & rng) const {    ...    return std::normal_distribution<>(mean(), sigma())(rng); } 

I wrote it so that the first few iterations were not taken into account, to eliminate the effect of memory latencies.

The result is a test program that can select the best algorithm for the input data, with optional modes that use the reference implementation of LZ4 or a specific version of the algorithm.

So there are six options:
— Reference (baseline): original LZ4 without our modifications.
— Variant 0: copy 8 bytes at a time without shuffle.
— Variant 1: copy 8 bytes at a time with shuffle.
— Variant 2: copy 16 bytes at a time without shuffle.
— Variant 3: copy 16 bytes at a time with shuffle.
— The "bandit" option, which selects the best of the four optimized variants.

Testing on different CPUs

If the result strongly depends on the CPU model, it would be interesting to find out exactly how it is affected. There might be an exceptionally large difference on certain CPUs.

I prepared a set of datasets from different tables in ClickHouse with real data, for a total of 256 different files each with 100 MB of uncompressed data (the number 256 was coincidental). Then I looked at the CPUs of the servers where I can run benchmarks. I found servers with the following CPUs:
— Intel® Xeon® CPU E5-2650 v2 @ 2.60GHz
— Intel® Xeon® CPU E5-2660 v4 @ 2.00GHz
— Intel® Xeon® CPU E5-2660 0 @ 2.20GHz
— Intel® Xeon® CPU E5645 @ 2.40GHz
— Intel Xeon E312xx (Sandy Bridge)
— AMD Opteron(TM) Processor 6274
— AMD Opteron(tm) Processor 6380
— Intel® Xeon® CPU E5-2683 v4 @ 2.10GHz
— Intel® Xeon® CPU E5530 @ 2.40GHz
— Intel® Xeon® CPU E5440 @ 2.83GHz
— Intel® Xeon® CPU E5-2667 v2 @ 3.30GHz

The most interesting part comes next — the processors provided by the R&D department:
— AMD EPYC 7351 16-Core Processor, a new AMD server processor.
— Cavium ThunderX2, which is AArch64, not x86. For these, my SIMD optimization needed to be reworked a bit. The server has 224 logical and 56 physical cores.

There are 13 servers in total, and each of them runs the test on 256 files in 6 variants (reference, 0, 1, 2, 3, adaptive). The test is run 10 times, alternating between the options in random order. It outputs 199,680 results that we can compare.

For example, we can compare different CPUs with each other. But we shouldn't jump to conclusions from these results, because we are only testing the LZ4 decompression algorithm on a single core (this is a very narrow case, so we only get a micro-benchmark). For example, the Cavium has the lowest performance per single core. But I tested ClickHouse on it myself, and it wins out over Xeon E5-2650 v2 on heavy queries due to the greater number of cores, even though it is missing many optimizations that are made in ClickHouse specifically for the x86.

 ┌─cpu───────────────────┬──ref─┬─adapt─┬──max─┬─best─┬─adapt_boost─┬─max_boost─┬─adapt_over_max─┐
│ E5-2667 v2 @ 3.30GHz │ 2.81 │ 3.19 │ 3.15 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2650 v2 @ 2.60GHz │ 2.5 │ 2.84 │ 2.81 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2683 v4 @ 2.10GHz │ 2.26 │ 2.63 │ 2.59 │ 3 │ 1.16 │ 1.15 │ 1.02 │
│ E5-2660 v4 @ 2.00GHz │ 2.15 │ 2.49 │ 2.46 │ 3 │ 1.16 │ 1.14 │ 1.01 │
│ AMD EPYC 7351 │ 2.03 │ 2.44 │ 2.35 │ 3 │ 1.20 │ 1.16 │ 1.04 │
│ E5-2660 0 @ 2.20GHz │ 2.13 │ 2.39 │ 2.37 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E312xx (Sandy Bridge) │ 1.97 │ 2.2 │ 2.18 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E5530 @ 2.40GHz │ 1.65 │ 1.93 │ 1.94 │ 3 │ 1.17 │ 1.18 │ 0.99 │
│ E5645 @ 2.40GHz │ 1.65 │ 1.92 │ 1.94 │ 3 │ 1.16 │ 1.18 │ 0.99 │
│ AMD Opteron 6380 │ 1.47 │ 1.58 │ 1.56 │ 1 │ 1.07 │ 1.06 │ 1.01 │
│ AMD Opteron 6274 │ 1.15 │ 1.35 │ 1.35 │ 1 │ 1.17 │ 1.17 │ 1 │
│ E5440 @ 2.83GHz │ 1.35 │ 1.33 │ 1.42 │ 1 │ 0.99 │ 1.05 │ 0.94 │
│ Cavium ThunderX2 │ 0.84 │ 0.87 │ 0.87 │ 0 │ 1.04 │ 1.04 │ 1 │
└───────────────────────┴──────┴───────┴──────┴──────┴─────────────┴───────────┴────────────────┘ 

• ref, adapt, max — The speed in gigabytes per second (the value that is the reverse of the arithmetic mean of time for all launches on all datasets).
• best — The number of the best algorithm among the optimized variants, from 0 to 3.
• adapt_boost — The relative advantage of the adaptive algorithm compared to the baseline.
• max_boost — The relative advantage of the best of the non-adaptive variants compared to the baseline.
• adapt_over_max — The relative advantage of the adaptive algorithm over the best non-adaptive one.

The results show that we were able to speed up decompression by 12-20% on modern x86 processors. Even on ARM we saw 4% improvement, despite the fact that we didn't optimize much for this architecture. It is also clear that on average for different datasets, the "bandit" algorithm comes out ahead of the pre-selected best variant on all processors (except for very old Intel CPUs).

Conclusión

In practice, the usefulness of this work is dubious. Yes, LZ4 decompression was accelerated on average by 12-20%, and on some datasets the performance more than doubled. But in general, this doesn't have much effect on query execution time. It's difficult to find real queries that gain more than a couple percent in speed.

We decided to use ZStandard level 1 instead of LZ4 on several Yandex Metrica clusters intended for executing long queries, because it is more important to save IO and disk space on cold data. Keep this in mind if you have similar workload.

We observed the greatest benefits from optimizing decompression in highly compressible data, such as columns with mostly duplicate string values. However, we have developed a separate solution specifically for this scenario that allows us to significantly speed up queries over this kind of data.

Another point to remember is that optimization of decompression speed is often limited by the format of the compressed data. LZ4 uses a very good format, but Lizard, Density and LZSSE have other formats that can work faster. Perhaps instead of trying to accelerate LZ4, it would be better to just integrate LZSSE into ClickHouse.

It's unlikely that these optimizations will be implemented in the mainstream LZ4 library: in order to use them, the library interface would have to be modified. In fact, this is often the case with improving algorithms — optimizations don't fit into old abstractions and they have to be revised. However, variable names have already been corrected in the original implementation. For instance, inc and dec tables have been corrected . In addition, about a month ago, the original implementation accelerated decompression by the same 12-15% by copying 32 bytes instead of 16, as discussed above. We tried the 32-byte option ourselves and the results were not that great, but they were still faster .

If you look at the profile at the beginning of the article, you may notice that we could have removed one extra copying operation from the page cache to userspace (either using mmap , or using O_DIRECT and userspace page cache, but both options are problematic). We also could have slightly improved the checksum calculation (CityHash128 is currently used without CRC32-C, but we could use HighwayHash, FARSH or XXH3). Acceleration of these two operations is useful for weakly compressed data, since they are performed on compressed data.

In any case, the changes have already been added to master more than a year ago, and the ideas that resulted from this research have been applied in other tasks. You can also watch the video from HighLoad++ Siberia, or view the presentation (both in Russian).