La propiedad de simetría de la relación de cointegración.

El propósito de este artículo es compartir resultados paradójicos en el estudio de la cointegración de series temporales : si las series temporales $$$A$ co-integrado con cercano $$$B$ remar $$$B$ no siempre co-integrado con un número $$$A$ .

Si estudiamos la cointegración puramente teórica, entonces es fácil demostrar que si la serie $$$A$ cointegrado con $$$B$ luego remar $$$B$ cointegrado con $$$A$ . Sin embargo, si comenzamos a estudiar la cointegración empíricamente, resulta que los cálculos teóricos no siempre se confirman. ¿Por qué está pasando esto?

Simetría

Actitud $$$A$ llamado simétrico si $$$A \ subseteq A ^ {- 1}$ donde $$$A ^ {- 1}$ - la relación inversa definida por la condición: $$$x A ^ {- 1} y$ equivalente a $$$yAx$ . En otras palabras, si la relación $$$xAy$ entonces la relación $$$yAx$ .

Considerar dos $$$I (1)$ una serie de $$$x_t$ y $$$y_t$ , $$$t = 0, \ puntos, T$ . La cointegración es simétrica si $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ implica $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ es decir, si la presencia de regresión directa conduce a la presencia de la inversa.

Considera la ecuación $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ , $$$\ beta_1 \ neq 0$ . Cambia los lados izquierdo y derecho y resta $$$\ varepsilon_ {1t}$ de ambas partes: $$$\ beta_1 x_t = y_t - \ varepsilon_ {1t}$ . Desde $$$\ beta_1 \ neq 0$ por definición, divida ambas partes en $$$\ beta_1$ :

$$

$$x_t = \ frac {1} {\ beta_1} y_t - \ frac {\ varepsilon_ {1t}} {\ beta_1}.$$

Reemplazar $$$1 / \ beta_1$ en $$$\ beta_2$ y $$$- \ varepsilon_ {1t} / \ beta_1$ en $$$\ varepsilon_ {2t}$ tenemos $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ . Por lo tanto, la relación de cointegración es simétrica.

Se deduce que si la variable $$$X$ cointegrado con variable $$$Y$ entonces la variable $$$Y$ debe cointegrarse con la variable $$$X$ . Sin embargo, la prueba de cointegración Angle-Granger no siempre confirma esta propiedad de simetría, ya que a veces una variable $$$Y$ no co-integrado con variable $$$X$ De acuerdo con esta prueba.

Probé la propiedad de simetría en los datos de 2017 de los intercambios de Moscú y Nueva York usando la prueba Angle-Granger. Había 7.975 pares de acciones cointegradas en la Bolsa de Moscú. Para 7731 (97%) pares cointegrados, se confirmó la propiedad de simetría, para 244 (3%) pares cointegrados no se confirmó la propiedad de simetría.

Había 140,903 pares de acciones cointegradas en la Bolsa de Nueva York. Para 136586 (97%) pares cointegrados, se confirmó la propiedad de simetría, para 4317 (3%) pares cointegrados no se confirmó la propiedad de simetría.

Interpretación

Este resultado puede interpretarse por la baja potencia y la alta probabilidad de error del segundo tipo de prueba Dickey-Fuller, en la que se basa la prueba Angle-Granger. La probabilidad de un error del segundo tipo se puede denotar por $$$\ beta = P (H_0 | H_1)$ entonces el valor $$$1 - \ beta$ llamado el poder de la prueba. Desafortunadamente, la prueba de Dickey-Fuller no puede distinguir entre series de tiempo no estacionarias y casi no estacionarias.

¿Qué es una serie temporal casi inestable? Considera la serie de tiempo $$$x_t = \ phi x_ {t-1} + \ varepsilon_t$ . Una serie temporal estacionaria es una serie en la que $$$0 <\ phi <1$ . Una serie temporal no estacionaria es una serie en la que $$$\ phi = 1$ . Una serie temporal casi inestable es una serie en la que el valor $$$\ phi$ cerca de uno

En el caso de series de tiempo casi no estacionarias, a menudo no podemos rechazar la hipótesis nula de no estacionarias. Esto significa que la prueba de Dickey-Fuller tiene un alto riesgo de un segundo tipo de error, es decir, la probabilidad de no rechazar la hipótesis nula falsa.

Prueba KPSS

Una posible respuesta a la debilidad de la prueba Dickey-Fuller es la prueba KPSS, que debe su nombre a las iniciales de los científicos de Kvyatkovsky, Phillips, Schmidt y Sheen. Aunque el enfoque metodológico de esta prueba es completamente diferente del enfoque de Dickey-Fuller, la diferencia principal debe entenderse en la permutación de las hipótesis nula y alternativa.

En la prueba KPSS, la hipótesis nula establece que la serie temporal es estacionaria, frente a la alternativa sobre la presencia de no estacionariedad. Las series temporales casi no estacionarias, que a menudo se identificaron como no estacionarias mediante la prueba Dickey-Fuller, se pueden identificar correctamente como estacionarias mediante la prueba KPSS.

Sin embargo, debemos ser conscientes de que cualquier resultado de las pruebas estadísticas es meramente probabilístico y no debe confundirse con un cierto juicio verdadero. Siempre hay una probabilidad distinta de cero de que nos equivoquemos. Por esta razón, se propone combinar los resultados de las pruebas Dickey-Fuller y KPSS como una prueba ideal para la no estacionariedad.



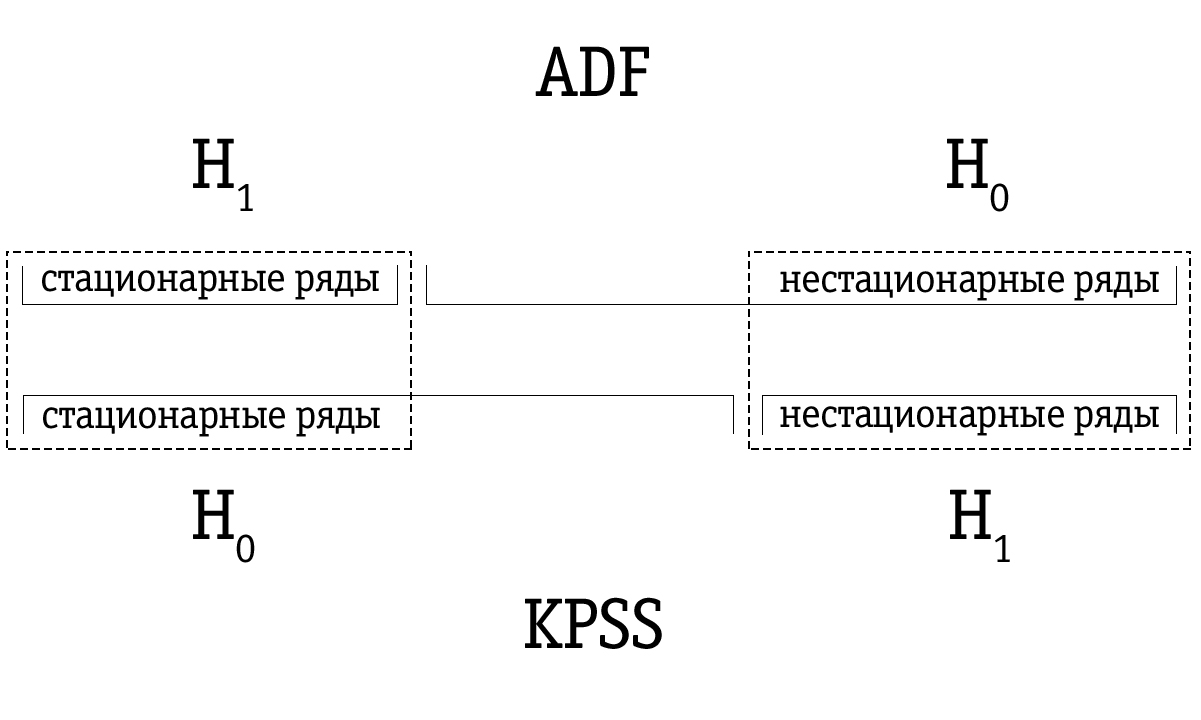
Debido a la baja potencia, la prueba de Dickey-Fuller a menudo identifica erróneamente una serie como no estacionaria, por lo que el conjunto resultante de series de tiempo identificadas por la prueba de Dickey-Fuller como inestable es mayor en comparación con muchas series de tiempo identificadas como no estacionarias usando la prueba KPSS. Por lo tanto, el orden de prueba es importante.

Si la serie de tiempo se identifica como estacionaria usando la prueba Dickey-Fuller, lo más probable es que también se identifique como estacionaria usando la prueba KPSS; en este caso, podemos suponer que la serie es estacionaria.

Si la serie temporal se identificó como inestable usando la prueba KPSS, entonces lo más probable es que también se identifique como inestable usando la prueba Dickey-Fuller; en este caso, podemos suponer que la serie es realmente inestable.

Sin embargo, a menudo sucede que una serie de tiempo que se ha identificado como no estacionaria usando la prueba Dickey-Fuller se marcará como estacionaria usando la prueba KPSS. En este caso, debemos ser muy cuidadosos con nuestra conclusión final. Podemos verificar cuán sólida es la base de la estacionariedad en el caso de la prueba KPSS y la inestabilidad en el caso de la prueba Dickey-Fuller y tomar una decisión adecuada. Por supuesto, también podemos dejar sin resolver la cuestión de la estacionariedad de una serie temporal de este tipo.

El enfoque de prueba de KPSS asume series de tiempo $$$y_t$ probado para la estacionalidad en relación con una tendencia puede descomponerse en la suma de una tendencia determinista $$$\ beta t$ paseo al azar $$$r_t$ y error estacionario $$$\ varepsilon_t$ :

$$

$$y_t = \ beta t + r_t + \ varepsilon_t, \\ r_t = r_ {t-1} + u_t,$$

donde $$$u_t$ - proceso iid normal con media y varianza cero $$$\ sigma ^ 2$ ( $$$u_t \ sim N (0, \ sigma ^ 2)$ ) Valor inicial $$$r_0$ tratado como fijo y desempeña el papel de un miembro libre. Error estacionario $$$\ varepsilon_t$ puede ser generado por cualquier proceso ARMA común, es decir, puede tener una fuerte autocorrelación.

Similar a la prueba de Dickey-Fuller, la capacidad de tener en cuenta una estructura arbitraria de autocorrelación $$$\ varepsilon_t$ muy importante porque la mayoría de las series de tiempo económicas dependen mucho del tiempo y, por lo tanto, tienen una fuerte autocorrelación. Si queremos verificar la estacionaria con respecto al eje horizontal, entonces el término $$$\ beta t$ simplemente excluido de la ecuación anterior.

De la ecuación anterior se deduce que la hipótesis nula $$$H_0$ sobre estacionariedad $$$y_t$ equivalente a la hipótesis $$$\ sigma ^ 2 = 0$ , de lo cual se deduce que $$$r_t = r_0$ para todos $$$t$ ( $$$r_0$ Es una constante). Del mismo modo, una hipótesis alternativa $$$H_1$ la no estacionariedad es equivalente a la hipótesis $$$\ sigma ^ 2 \ neq 0$ .

Para probar la hipótesis $$$H_0$ : $$$\ sigma ^ 2 = 0$ (serie temporal estacionaria) versus alternativa $$$H_1$ : $$$\ sigma ^ 2 \ neq 0$ (series de tiempo no estacionarias) los autores de la prueba KPSS reciben estadísticas unidireccionales de la prueba multiplicadora de Lagrange. También calculan su distribución asintótica y modelan los valores críticos asintóticos. Aquí no consideramos detalles teóricos, sino que resumimos brevemente el algoritmo de ejecución de la prueba.

Al realizar la prueba KPSS para una serie temporal $$$y_t$ , $$$t = 1, \ puntos, T$ El método de mínimos cuadrados (mínimos cuadrados) se utiliza para estimar una de las siguientes ecuaciones:

$$

$$y_t = a_0 + \ varepsilon_t, \\ y_t = a_0 + \ beta t + \ varepsilon_t.$$

Si queremos verificar la estacionariedad con respecto al eje horizontal, evaluamos la primera ecuación. Si planeamos verificar la estacionariedad con respecto a la tendencia, elegimos la segunda ecuación.

Restos $$$e_t$ de la ecuación estimada se utilizan para calcular las estadísticas de la prueba de multiplicadores de Lagrange. La prueba del multiplicador de Lagrange se basa en la idea de que cuando se cumple la hipótesis nula, todos los multiplicadores de Lagrange deben ser iguales a cero.

Prueba de multiplicador de Lagrange

La prueba del multiplicador de Lagrange se asocia con un enfoque más general para la estimación de parámetros utilizando el método de máxima verosimilitud (ML). Según este enfoque, los datos se consideran evidencia relacionada con los parámetros de distribución. La evidencia se expresa en función de parámetros desconocidos, una función de probabilidad:

$$

$$L (X_1, X_2, X_3, \ dots, X_n; \ Phi_1, \ Phi_2, \ dots, \ Phi_k),$$

donde $$$X_i$ Son los valores observados, y $$$\ Phi_i$ - parámetros que queremos evaluar.

La función de máxima verosimilitud es la probabilidad conjunta de observaciones de muestra.

$$

$$L (X_1, X_2, X_3, \ dots, X_n; \ Phi_1, \ Phi_2, \ dots, \ Phi_k) = P (X_1 \ land X_2 \ land X_3 \ dots X_n).$$

El objetivo del método de máxima verosimilitud es maximizar la función de verosimilitud. Esto se logra diferenciando la función de probabilidad máxima para cada uno de los parámetros estimados y equiparando las derivadas parciales a cero. Los valores de los parámetros en los que el valor de la función es máximo es la estimación deseada.

Por lo general, para simplificar el trabajo posterior, primero se toma el logaritmo de la función de probabilidad.

Considere un modelo lineal generalizado $$$Y = \ beta X + \ varepsilon$ donde se supone que $$$\ varepsilon$ normalmente distribuido $$$N (0, \ sigma ^ 2)$ eso es $$$Y - \ beta X \ sim N (0, \ sigma ^ 2)$ .

Queremos probar la hipótesis de que el sistema $$$q$ ( $$$q <k$ ) restricciones lineales independientes $$$R \ beta = r$ . Aqui $$$R$ - famoso $$$q \ veces k$ matriz de rango $$$q$ y $$$r$ - famoso $$$q \ veces 1$ vector

Para cada par de valores observados $$$X$ y $$$Y$ En condiciones normales, existirá una función de densidad de probabilidad de la siguiente forma:

$$

$$f (X_i, Y_i) = \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ left (\ frac {Y_i - \ beta X_i} {\ sigma} \ right) ^ 2}.$$

Sujeto a $$$n$ observaciones conjuntas $$$X$ y $$$Y$ La probabilidad total de observar todos los valores de la muestra es igual al producto de los valores individuales de la función de densidad de probabilidad. Por lo tanto, la función de probabilidad se define de la siguiente manera:

$$

$$L (\ beta) = \ prod \ limits_ {i = 1} ^ n \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ left (\ frac {Y_i - \ beta X_i} {\ sigma} \ right) ^ 2}.$$

Como es más fácil diferenciar la suma que el producto, generalmente se toma el logaritmo de la función de probabilidad, por lo tanto:

$$

$$\ ln L (\ beta) = \ sum \ limits_ {i = 1} ^ n \ left (\ ln \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} - \ frac {1} { 2 \ sigma ^ 2} (Y_i - \ beta X_i) ^ 2 \ right).$$

Esta útil conversión no afecta el resultado final, porque $$$\ ln L$ Es una función creciente $$$L$ . Entonces el valor $$$\ beta$ que maximiza $$$\ ln L$ también maximizará $$$L$ .

Puntuación de ML para $$$\ beta$ en regresión con restricción ( $$$R \ beta = r$ ) se obtiene maximizando la función $$$\ ln L (\ beta)$ sujeto a $$$R \ beta = r$ . Para encontrar esta estimación, escribimos la función Lagrange:

$$

$$\ psi (\ beta) = \ ln L (\ beta) - g '(R \ beta - r),$$

por donde $$$g = \ left (g_1, \ dots, g_q \ right) '$ vector marcado $$$q$ Multiplicadores de Lagrange.

Estadísticas de prueba de multiplicador de Lagrange denotadas por $$$\ eta_ \ mu$ en caso de estacionaria con respecto al eje horizontal y a través de $$$\ eta_ \ tau$ en caso de estacionariedad relativa a la tendencia, está determinada por la expresión

$$

$$\ eta _ {\ mu / \ tau} = T ^ 2 \ frac {1} {s ^ 2 (l)} \ sum \ limits_ {t = 1} ^ T S_t ^ 2,$$

donde

$$

$$S_t = \ sum \ limits_ {i = 1} ^ t e_i$$

y

$$

$$s ^ 2 (l) = T ^ {- 1} \ sum \ limits_ {t = 1} ^ T e_t ^ 2 + 2 T ^ {- 1} \ sum \ limits_ {1} ^ lw (s, l) \ sum \ limits_ {t = s + 1} ^ T e_t e_ {ts},$$

donde

$$

$$w (s, l) = 1 - \ frac {s} {l + 1}.$$

En las ecuaciones anteriores $$$S_t$ - el proceso de saldos parciales $$$e_t$ de la ecuación estimada; $$$s ^ 2 (l)$ - evaluación de la dispersión de residuos a largo plazo $$$e_t$ ; pero $$$w (s, l)$ - la llamada ventana espectral de Bartlett, donde $$$l$ - parámetro de truncamiento de retraso.

En esta aplicación, la ventana espectral se usa para estimar la densidad espectral de los errores para un determinado intervalo (ventana), que se mueve a lo largo de todo el rango de la serie. Los datos fuera del intervalo se ignoran, ya que la función de ventana es una función igual a cero fuera de algún intervalo seleccionado (ventana).

Estimación de varianza $$$s ^ 2 (l)$ depende del parámetro $$$l$ y desde $$$l$ aumenta y más de 0, puntuación $$$s ^ 2 (l)$ comienza a tener en cuenta la posible autocorrelación en residuos $$$e_t$ .

Finalmente, las estadísticas de prueba del multiplicador de Lagrange $$$\ eta_ \ mu$ o $$$\ eta_ \ tau$ se compara con los valores críticos Si las estadísticas de la prueba del multiplicador de Lagrange exceden el valor crítico correspondiente, entonces la hipótesis nula $$$H_0$ (series temporales estacionarias) se desvía a favor de una hipótesis alternativa $$$H_1$ (series de tiempo no estacionarias). De lo contrario, no podemos rechazar la hipótesis nula $$$H_0$ sobre la estacionariedad de una serie temporal.

Los valores críticos son asintóticos y, por lo tanto, son más adecuados para muestras de gran tamaño. Sin embargo, en la práctica también se utilizan para una muestra pequeña. Además, los valores críticos son independientes del parámetro. $$$l$ . Sin embargo, las estadísticas de la prueba del multiplicador de Lagrange dependerán del parámetro $$$l$ . Los autores de la prueba KPSS no ofrecen ningún algoritmo general para elegir el parámetro apropiado. $$$l$ . La prueba generalmente se realiza para $$$l$ en el rango de 0 a 8.

Con aumento $$$l$ somos menos propensos a rechazar la hipótesis nula $$$H_0$ sobre la estacionariedad, que en parte conduce a una disminución en el poder de la prueba y puede dar resultados mixtos. Sin embargo, en general, podemos decir que si la hipótesis nula $$$H_0$ la estacionariedad de la serie temporal no se rechaza incluso con valores pequeños $$$l$ (0, 1 o 2), concluimos que las series de tiempo verificadas son estacionarias.

Comparación de resultados de prueba

La siguiente metodología fue desarrollada para evaluar la probabilidad de simetría.

1. Todas las series temporales se verifican para la integrabilidad de primer orden utilizando la prueba Dickey-Fuller a un nivel de significancia de 0.05. Solo se consideran a continuación series integrables de primer orden.
2. Las series integrables de primer orden obtenidas en la Sección 1 comprenden pares mediante la combinación sin repetición.
3. Los pares de acciones elaborados en la cláusula 2 se prueban para la cointegración utilizando la prueba Angle-Granger. Como resultado, se identifican pares cointegrados.
4. Los residuos de regresión obtenidos como resultado de las pruebas en el párrafo 3 se prueban para la estacionariedad utilizando la prueba KPSS. Por lo tanto, los resultados de las dos pruebas se combinan.
5. Las series de tiempo en los pares cointegrados de la Sec. 2 se intercambian y se verifica nuevamente para la cointegración usando la prueba Angle-Granger, es decir, examinamos si la relación entre series de tiempo es simétrica.
6. Las series de tiempo en los pares cointegrados del ítem 4 se intercambian y los residuales de la regresión se verifican nuevamente para determinar la estacionariedad utilizando la prueba KPSS, es decir, examinaremos si la relación entre las series de tiempo es simétrica.

Todos los cálculos se realizan con el paquete MATLAB. Los resultados se presentan en la tabla a continuación. Para cada prueba, tenemos una serie de relaciones simétricas de acuerdo con los resultados de la prueba (marcados $$$S$ ); tenemos una serie de relaciones que no son simétricas según los resultados de la prueba (marcadas $$$¬S$ ); y tenemos una probabilidad empírica de que la relación sea simétrica de acuerdo con los resultados de la prueba ( $$$P (S) = \ frac {S} {S + ¬S}$ )

En el intercambio de Moscú:


En la Bolsa de Nueva York:

Comparación de resultados de backtest

Comparemos los resultados de una estrategia comercial en datos históricos para pares cointegrados seleccionados usando la prueba Angle-Granger y para pares cointegrados seleccionados usando la prueba KPSS.

Como se puede ver en la tabla, debido a una identificación más precisa de los pares de acciones cointegrados, fue posible aumentar el rendimiento anual promedio al negociar un par cointegrado por separado en un 9.21%. Por lo tanto, la metodología propuesta puede aumentar la rentabilidad del comercio algorítmico utilizando estrategias neutrales en el mercado.

Interpretación alternativa

Como vimos anteriormente, los resultados de la prueba Angle-Granger son una lotería. Para algunos, mis pensamientos parecerán excesivamente categóricos, pero creo que tiene mucho sentido no tomar la hipótesis nula, confirmada por análisis estadístico, sobre la fe.

El conservadurismo del método científico para probar hipótesis es que al analizar los datos solo podemos hacer una conclusión válida: la hipótesis nula se rechaza en el nivel de significación elegido. Esto no significa que la alternativa sea verdadera. $$$H_1$ - acabamos de recibir evidencia indirecta de su credibilidad sobre la base de una típica "evidencia de lo contrario". En el caso cuando es verdad $$$H_0$ , el investigador también tiene instrucciones de llegar a una conclusión cautelosa: en base a los datos obtenidos en las condiciones experimentales, no fue posible encontrar suficiente evidencia para rechazar la hipótesis nula.

Al unísono con mis pensamientos en septiembre de 2018, personas influyentes escribieron un artículo llamando a abandonar el concepto de "significación estadística" y el paradigma de probar la hipótesis nula.

Lo más importante: "Sugerencias como cambiar el nivel de umbral $$valores p por defecto, usando intervalos de confianza con énfasis en si contienen cero o no, o usando el coeficiente de Bayes junto con clasificaciones universalmente aceptadas para evaluar la fuerza de la evidencia que proviene de los mismos problemas o problemas similares al uso actual$p$$$$p$ - 0,05… , , „ “ (Gelman, 2016), — , „ “ „ “ — $$$p$ - .

(Carlin, 2016; Gelman, 2016), , ( ) , , .»

Conclusiones

Vimos que, aunque la propiedad de simetría de la relación de cointegración debería cumplirse teóricamente, los datos experimentales divergen de los cálculos teóricos. Una de las interpretaciones de esta paradoja es el bajo poder de la prueba Dickey-Fuller.

Como una nueva metodología para identificar pares de activos cointegrados, se propuso probar los residuos de regresión obtenidos usando la prueba Angle-Granger para la estacionariedad usando la prueba KPSS y combinar los resultados de estas pruebas; y combine los resultados de la prueba Angle-Granger y la prueba KPSS para la regresión directa e inversa.

Se realizaron backtests sobre los datos de la Bolsa de Moscú de 2017. De acuerdo con los resultados de las pruebas retrospectivas, el rendimiento anual promedio cuando se utiliza la metodología para identificar pares de acciones cointegradas propuestas anteriormente fue del 22.72%. Por lo tanto, en comparación con la identificación de pares de existencias cointegradas mediante la prueba Angle-Granger, fue posible aumentar el rendimiento anual promedio en un 9.21%.

Una interpretación alternativa de la paradoja es no tomar la hipótesis nula, confirmada por análisis estadístico, sobre la fe. El paradigma de prueba de hipótesis nulas y la dicotomía que ofrece dicho paradigma nos dan una falsa sensación de conocimiento del mercado.

Cuando recién comencé mi investigación, me pareció que podía tomar el mercado, ponerlo en la "picadora de carne" de las pruebas estadísticas y obtener filas sabrosas filtradas a la salida. Desafortunadamente, ahora veo que este concepto de fuerza bruta estadística no funcionará.

Ya sea que haya cointegración en el mercado o no, para mí esta pregunta sigue abierta. Todavía tengo grandes preguntas para los fundadores de esta teoría. Solía ​​sentir cierta inquietud en Occidente y en aquellos científicos que desarrollaron matemáticas financieras en un momento en que la econometría se consideraba una burguesía corrupta en la Unión Soviética. Me pareció que estábamos muy lejos, y en algún lugar de Europa y América estaban sentados los dioses de las finanzas, que conocían el sagrado grial de la verdad.

Ahora entiendo que los científicos europeos y estadounidenses no son muy diferentes de los nuestros, la única diferencia está en la escala de la charlatanería. Nuestros científicos están sentados en un castillo de marfil, escriben algunas tonterías y reciben subvenciones por un monto de 500 mil rublos. En Occidente, casi los mismos científicos están sentados en el mismo castillo de marfil, escriben sobre el mismo sinsentido y obtienen "nobel" y subvenciones por la cantidad de 500 mil dólares para esto. Esa es toda la diferencia.

Por el momento, no tengo una visión clara del tema de mi investigación. Es incorrecto decir que "todos los fondos de cobertura utilizan el comercio de pares" porque la mayoría de los fondos de cobertura también quiebran.

Desafortunadamente, siempre tiene que pensar y tomar decisiones con su propia cabeza, especialmente cuando arriesgamos dinero.