La programación dinámica tiene una reputación por el método que estudias en la universidad y luego solo recuerdas durante las entrevistas. Pero, de hecho, el método es aplicable en muchas situaciones. De hecho, esta es una técnica para resolver problemas de manera efectiva que se puede dividir en muchas subtareas altamente repetitivas .

En el artículo mostraré una interesante aplicación real de programación dinámica: la tarea de tallado de costuras. La tarea y la metodología se describen en detalle en el trabajo de Avidan y Shamir "Cortar costuras para cambiar el tamaño de las imágenes en función del contenido" (artículo de dominio público).

Este es uno de una serie de artículos sobre programación dinámica. Si desea repasar los métodos, consulte la introducción ilustrada a la programación dinámica .

Cambiar el tamaño de la imagen según el contenido

Para resolver un problema real mediante la programación dinámica, debe formularlo correctamente. Esta sección describe los ajustes preestablecidos necesarios para la tarea seleccionada.

Los autores del artículo original describen el cambio de tamaño de la imagen orientada al contenido, es decir, cambiar el ancho o la altura de la imagen en función del contenido. Vea el trabajo original para más detalles, y ofrezco una breve descripción. Supongamos que desea cambiar el tamaño de una foto de un surfista:


Vista superior de un surfista en medio de un océano tranquilo, con olas turbulentas a la derecha. Foto: Kiril Dobrev en Pixabay

Como se describe en detalle en el artículo, hay varias formas de reducir el ancho de la imagen: estos son el recorte y la escala estándar, con sus desventajas inherentes, así como la eliminación de columnas de píxeles del medio. Como puede imaginar, esto deja una costura visible en la foto, donde la imagen de la izquierda y la derecha no coinciden. Y de esta manera, puede eliminar solo una cantidad limitada de imagen.


Un intento de reducir el ancho recortando el lado izquierdo y cortando el bloque del medio. Este último deja una costura visible.

Avidan y Shamir en el artículo describen la nueva técnica de "tallado de costuras". Primero identifica áreas menos importantes de "baja energía" y luego calcula las "costuras" de baja energía que pasan a través de la imagen. En el caso de reducir el ancho de la imagen, se determina una costura vertical desde la parte superior de la imagen hacia la parte inferior, que en cada línea se desplaza hacia la izquierda o hacia la derecha en no más de un píxel.

En la foto del surfista, la costura de energía más baja corre por el medio de la imagen, donde el agua es más tranquila. Esto es consistente con nuestra intuición.


La costura de menor energía encontrada en la imagen del surfista se muestra con una línea roja de cinco píxeles de ancho para visibilidad, aunque de hecho la costura tiene solo un píxel de ancho.

Una vez determinada la costura con la menor energía y luego eliminándola, reducimos el ancho de la imagen en un píxel. Repetir este proceso una y otra vez reduce significativamente el ancho de toda la foto.


Imagen de surfista después de la reducción de ancho en 1024 píxeles

Nuevamente, el algoritmo eliminó lógicamente el agua inmóvil en el medio, así como en el lado izquierdo de la foto. Pero a diferencia del cultivo, la textura del agua de la izquierda se conserva y no hay transiciones bruscas. Es cierto que puede encontrar algunas transiciones imperfectas en el centro, pero básicamente el resultado parece natural.

Definición de energía de imagen

La magia es encontrar la costura de energía más baja. Para hacer esto, primero asignamos energía a cada píxel en la imagen. Luego, usamos la programación dinámica para encontrar el camino a través de la imagen con la menor energía: este algoritmo se discutirá en detalle en la siguiente sección. Primero, veamos cómo asignar valores de energía de píxeles.

El artículo científico discute varias funciones energéticas y sus diferencias. No lo compliquemos y tomemos una función que simplemente capture la cantidad de cambio de color alrededor de cada píxel. Para completar la imagen, describiré la función de energía con más detalle en caso de que desee implementarla usted mismo, pero esto es solo un preajuste para los cálculos de programación dinámica posteriores.


A la izquierda hay tres píxeles de oscuro a claro. La diferencia entre el primero y el último es genial. Tres píxeles oscuros a la derecha con una ligera diferencia en la intensidad del color.

Para calcular la energía de un píxel específico, mire los píxeles a la izquierda y a la derecha del mismo. En cuanto a los componentes, calculamos el cuadrado de la distancia entre ellos, es decir, el cuadrado de la diferencia entre los componentes rojo, verde y azul, y luego los sumamos. Hacemos lo mismo para los píxeles arriba y abajo del centro. Finalmente, suma las distancias horizontal y vertical.

$$

$$| \ Delta x | ^ 2 = (\ Delta r_x) ^ 2 + (\ Delta g_x) ^ 2 + (\ Delta b_x) ^ 2$$

$$

$$| \ Delta y | ^ 2 = (\ Delta r_y) ^ 2 + (\ Delta g_y) ^ 2 + (\ Delta b_y) ^ 2$$

$$

$$e (x, y) = | \ Delta x | ^ 2 + | \ Delta y | ^ 2$$

La única advertencia: por ejemplo, si un píxel está en el borde izquierdo, entonces no hay vecino a la izquierda. En este caso, solo comparamos con el píxel correcto. Se realizan verificaciones similares para los píxeles en los bordes superior, derecho e inferior.

La función de energía es excelente si los píxeles vecinos son muy diferentes en color y pequeños si son similares.


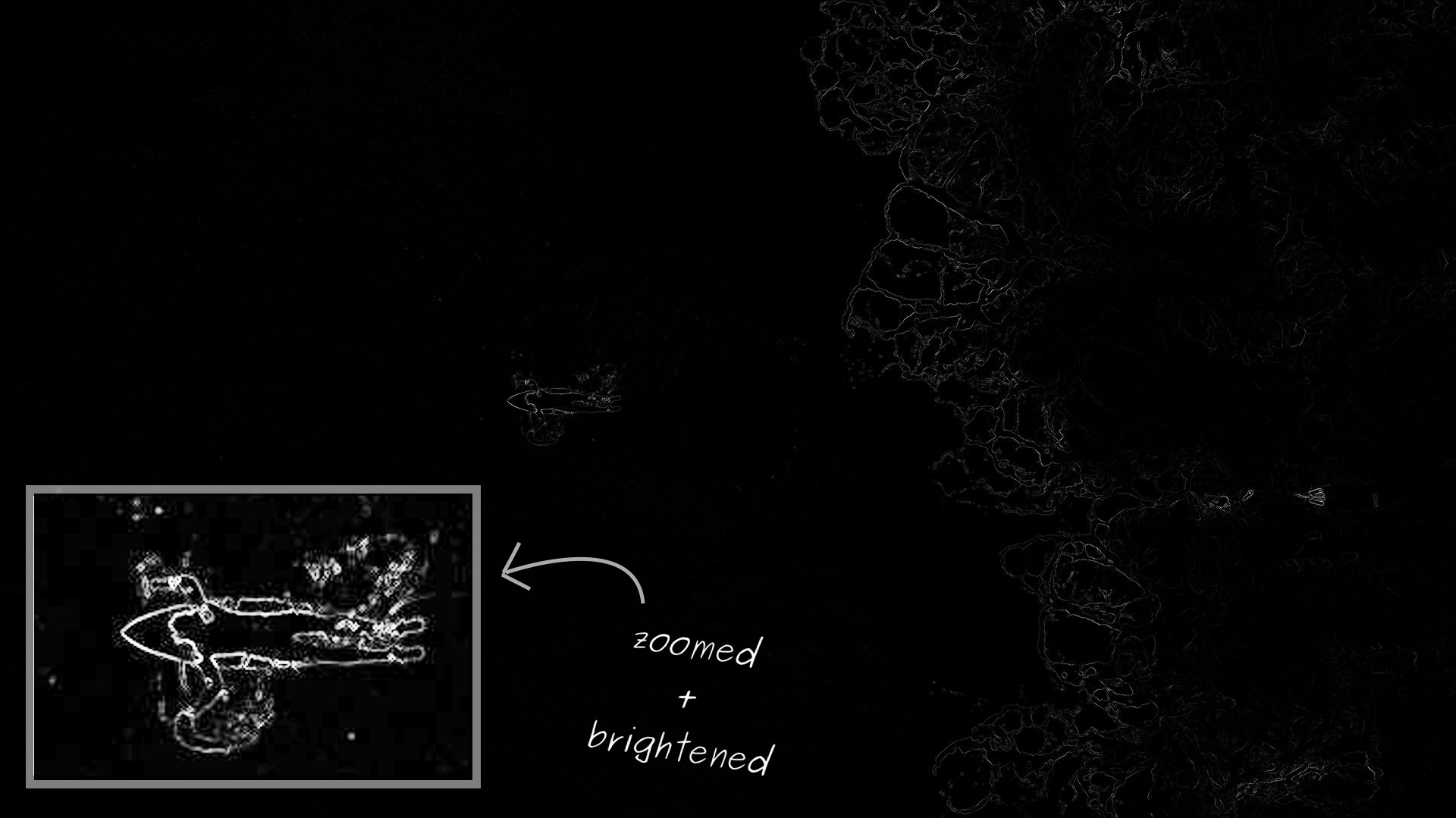La energía de cada píxel en la foto de un surfista: cuanto más claro, más alto es. Como se esperaba, el surfista tiene la energía más alta en las olas medias y turbulentas a la derecha

La función de energía funciona bien en una foto de surfista. Sin embargo, se necesita un rango muy amplio de valores. Por lo tanto, al renderizar, parece que en la mayoría de las fotos los píxeles tienen energía cero. De hecho, simplemente hay valores muy bajos en comparación con las regiones con la mayor energía. Para simplificar la visualización, amplié el navegador y resalté esta área.

Busque costuras de baja energía con programación dinámica

Al calcular la energía de cada píxel, podemos encontrar la costura con la energía más baja desde la parte superior de la imagen hasta la parte inferior. El mismo análisis se aplica a las costuras horizontales para reducir la altura de la imagen original. Sin embargo, nos centraremos en los verticales.

Comencemos con la definición:

• Una costura es una secuencia de píxeles, un píxel por línea. El requisito es que entre dos líneas consecutivas la coordenada $$$x$cambios por no más de un píxel. Esto preserva la secuencia de la costura.
  
• La costura con la energía más baja es aquella cuya energía total sobre todos los píxeles en la costura se minimiza.

Es importante tener en cuenta que la unión con la energía más baja no necesariamente atraviesa todos los píxeles con la energía más baja. Se tiene en cuenta la energía total de todos, no los píxeles individuales.


El enfoque codicioso no funciona. Al elegir un píxel de baja energía en una etapa temprana, nos quedamos atrapados en la región de alta energía de la imagen (camino rojo a la derecha)

Como puede ver, no puede seleccionar el píxel de menor energía en la siguiente línea.

Rompemos el problema en subtareas

El problema con el enfoque codicioso es que al decidir el siguiente paso, no tomamos en cuenta el resto de la costura por delante. No podemos mirar hacia el futuro, pero podemos tener en cuenta todo lo que ya sabemos.

Pongamos la tarea al revés. En lugar de elegir entre varios píxeles para continuar una costura, elegiremos entre varias costuras para ir a un píxel . Lo que debemos hacer es tomar cada píxel y elegir entre los píxeles en la línea de arriba, de donde puede salir la costura. Si cada uno de los píxeles en la línea de arriba codifica la ruta recorrida hasta este punto, entonces esencialmente estamos viendo la historia completa hasta este punto.


Para cada píxel, estudiamos tres píxeles en la línea de arriba. Elección fundamental: ¿cuál de las costuras continuar?

Esto supone una subtarea para cada píxel en la imagen. La subtarea debe encontrar la mejor ruta a un píxel específico, por lo que es una buena idea asociar con cada píxel la energía de la costura de baja energía que termina en ese píxel .

A diferencia del enfoque codicioso, el enfoque anterior esencialmente intenta todos los caminos posibles a través de la imagen. Es solo que al verificar todas las rutas posibles, las mismas subtareas se resuelven una y otra vez, lo que hace que este enfoque sea una opción ideal para la programación dinámica.

Definición de una relación de recurrencia

Como de costumbre, ahora tenemos que formalizar la idea en una relación recursiva. Hay una subtarea correspondiente a cada píxel en la imagen original, por lo que las entradas a nuestra relación de recurrencia pueden ser solo coordenadas $$$x$y $$$y$de este píxel. Esto proporciona entradas enteras, lo que facilita la organización de subtareas, así como la capacidad de almacenar valores calculados previamente en una matriz bidimensional.

Definir una función $$$M (x, y)$, que representa la energía de la costura vertical con la menor energía. Comienza en la parte superior de la imagen y termina en un píxel $$$(x, y)$. Titulo $$$M$seleccionado como en el artículo científico original.

Primero, necesitas una versión básica. Todas las costuras que terminan en la línea superior tienen una longitud de solo un píxel. Por lo tanto, una costura con energía mínima es solo un píxel con energía mínima:

$$

$$M (x, 0) = e (x, 0)$$

Para los píxeles en las filas restantes, mire los píxeles en la parte superior. Dado que la costura debe ser continua, tenemos en cuenta solo tres píxeles ubicados en la parte superior izquierda, superior y superior derecha. De ellos seleccionamos la costura con la energía más baja, que termina en uno de estos píxeles, y agregamos la energía del píxel actual:

$$

$$M (x, y) = e (x, y) + \ min \ begin {cases} M (x - 1, y - 1) \\ M (x, y - 1) \\ M (x + 1, y - 1) \ end {cases}$$

Como una situación límite, considere el caso cuando el píxel actual está en el borde izquierdo o derecho de la imagen. En estos casos, omitimos $$$M (x-1, y-1)$para píxeles en el borde izquierdo o $$$M (x + 1, y-1)$en el borde derecho

Finalmente, necesita extraer la energía de la costura de baja energía, que cubre toda la altura de la imagen. Esto significa que miramos la línea inferior de la imagen y seleccionamos la costura de menor energía que termina en uno de estos píxeles. Para foto amplia $$$W$y alto $$$H$píxeles:

$$

$$\ min_ {0 \ le x <W} M (x, H - 1)$$

Entonces, tenemos una relación de recurrencia con todas las propiedades necesarias:

• Una relación de recurrencia tiene entradas enteras.
  
• La respuesta final es fácil de extraer de la relación.
  
• La proporción depende de uno mismo.

Verificación de la subtarea DAG (gráfico acíclico orientado)

Desde cada subtarea $$$M (x, y)$corresponde a un píxel de la imagen original, el gráfico de dependencia es muy fácil de visualizar. ¡Simplemente colóquelos en una cuadrícula bidimensional, como en la imagen original!


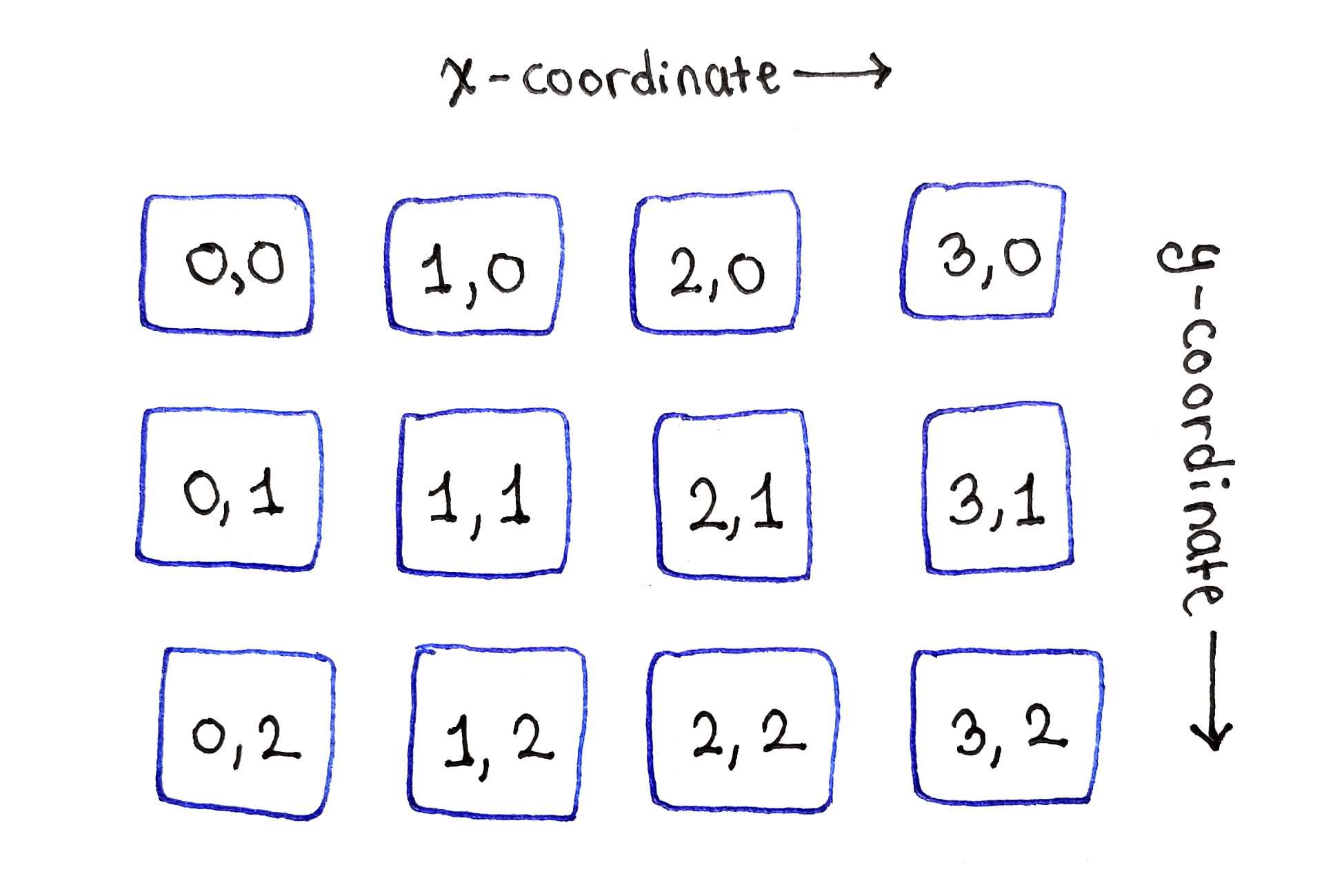Las subtareas se encuentran en una cuadrícula bidimensional, como los píxeles de la imagen original.

Como se deduce del escenario base de la relación de recurrencia, la línea superior de subtareas se puede inicializar con los valores de energía de píxeles individuales.


La fila superior es independiente de otras subtareas. Tenga en cuenta la ausencia de flechas de la fila superior de celdas

En la segunda línea, las dependencias comienzan a aparecer. En primer lugar, en la celda más a la izquierda en la segunda fila nos enfrentamos a una situación fronteriza. Como no hay celdas a la izquierda, la celda $$$(1,0)$depende solo de las celdas ubicadas directamente encima y en la esquina superior derecha. Lo mismo sucederá más tarde con la celda más a la izquierda en la tercera fila.


Las subtareas en el borde izquierdo dependen de solo dos subtareas por encima de ellas

En la segunda celda de la segunda fila (1,1), vemos la manifestación más típica de la relación de recurrencia. Esta celda depende de tres celdas: arriba a la izquierda, justo encima y arriba a la derecha. Esta estructura de dependencia se aplica a todas las celdas "intermedias" en la segunda fila y las siguientes.


Las subtareas entre los bordes izquierdo y derecho dependen de las tres subtareas en la parte superior

Finalmente, la celda en el borde derecho representa la segunda situación límite. Como no hay más celdas a la derecha, depende solo de las celdas directamente en la parte superior y superior izquierda.


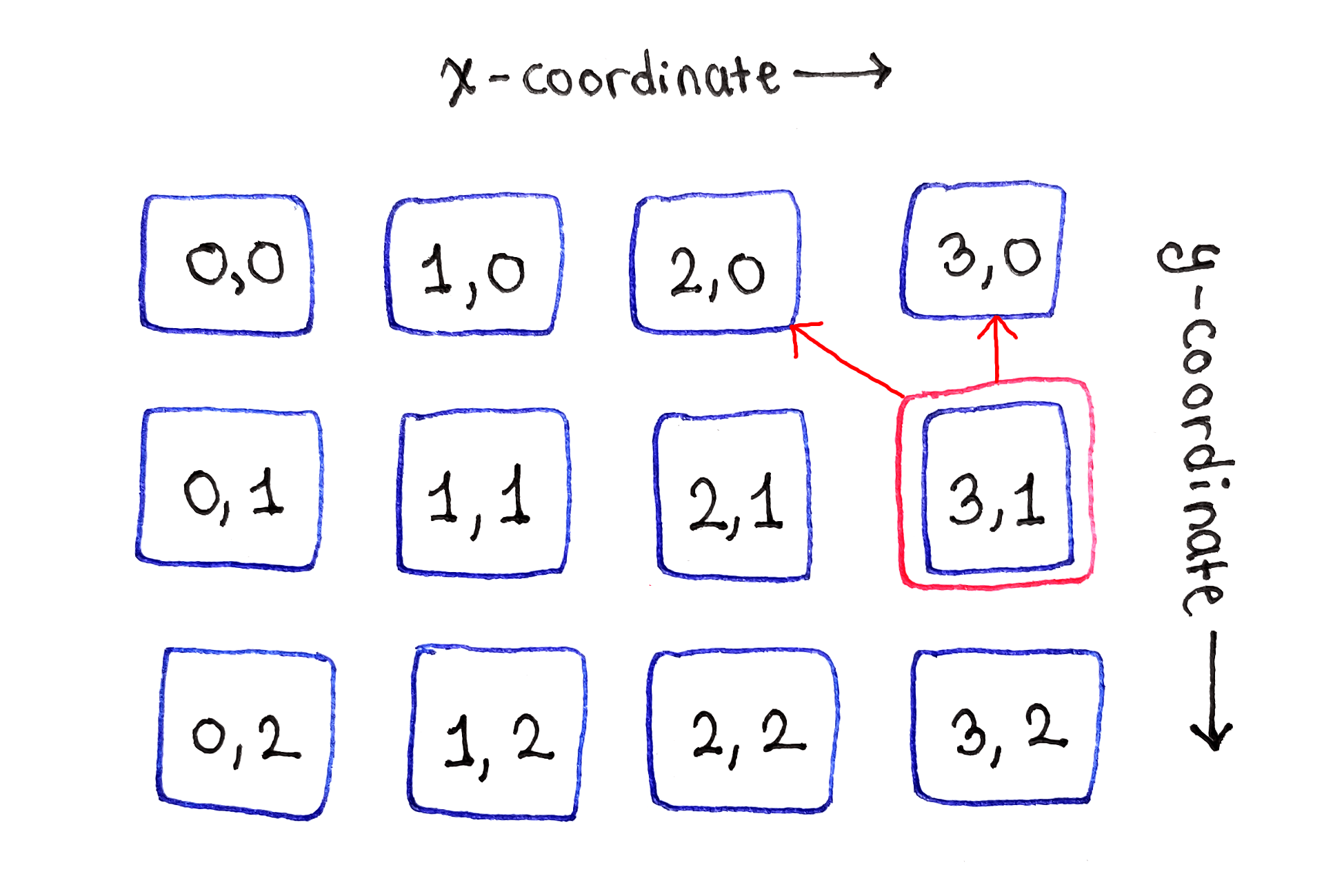Las subtareas en el borde derecho dependen de solo dos celdas en la parte superior

El proceso se repite para todas las líneas posteriores.


Como hay muchas flechas en el gráfico de dependencia, esta animación muestra las dependencias para cada subtarea a su vez

Un gráfico de dependencia completa lo asusta con una gran cantidad de flechas, pero mirarlas una por una ayuda a establecer patrones explícitos.

Implementación de abajo hacia arriba

Después de realizar este análisis, obtuvimos la orden de procesamiento:

• Ir desde la parte superior de la imagen hasta la parte inferior.
  
• Cada línea puede actuar en cualquier orden. La elección natural es ir de izquierda a derecha.

Dado que cada fila depende solo de la anterior, debe guardar solo dos filas de datos: una para la fila anterior y otra para la fila actual. Moviéndonos de izquierda a derecha, incluso podemos descartar elementos individuales de la fila anterior a medida que se usan. Sin embargo, esto complica el algoritmo, ya que tendrá que averiguar qué partes de la línea anterior se pueden descartar.

En el siguiente código de Python, la entrada es una lista de líneas, donde cada línea contiene una lista de números que representan las energías de píxeles individuales en esa línea. La entrada se llama pixel_energies , y pixel_energies[y][x] representa la energía del pixel en coordenadas $$$(x, y)$.

Comencemos calculando la energía de las costuras de la fila superior, simplemente copiando las energías de píxeles individuales en la fila superior:

 previous_seam_energies_row = list(pixel_energies[0]) 

Luego, pasamos por las líneas de entrada restantes, calculando las energías de costura para cada línea. La parte más "difícil" es determinar a qué elementos de la línea anterior hacer referencia, ya que no hay píxeles a la izquierda del borde izquierdo o a la derecha del borde derecho.

En cada iteración, se crea una nueva lista de energías de costura para la línea actual. Al final de la iteración, reemplazamos los datos de la línea anterior con los datos de la línea actual para la siguiente iteración. Así es como descartamos la línea anterior:

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_seam_energy = pixel_energy + \ min(previous_seam_energies_row[x_i] for x_i in x_range) seam_energies_row.append(min_seam_energy) previous_seam_energies_row = seam_energies_row 

Como resultado, previous_seam_energies_row contiene la energía de la costura para el resultado final. Encontramos el valor mínimo en esta lista, ¡y esta es la respuesta!

 min(seam_energy for seam_energy in previous_seam_energies_row) 

Puede probar esta implementación envolviendo el código en una función y luego llamándolo con la matriz bidimensional que creó. Se ha elegido la siguiente entrada para que falle el enfoque codicioso, con una costura obvia con la energía más baja:

 ENERGIES = [ [9, 9, 0, 9, 9], [9, 1, 9, 8, 9], [9, 9, 9, 9, 0], [9, 9, 9, 0, 9], ] print(min_seam_energy(ENERGIES)) 

Complejidad espacial y temporal.

Cada píxel en la imagen original corresponde a una subtarea. Para cada una de las subtareas, no hay más de tres dependencias, por lo que resolver cada una de ellas implica una cantidad constante de trabajo. La última fila se lleva a cabo dos veces. Entonces, para una imagen amplia $$$W$y alto $$$H$la complejidad del tiempo de píxeles es $$$O (ancho × alto + ancho)$.

En cada momento, tenemos dos listas: una para la línea anterior y otra para la actual. En el primero $$$W$elementos, y el segundo aumenta gradualmente a $$$W$. Por lo tanto, la complejidad espacial es igual a $$$O (2W)$eso es solo $$$O (w)$.

Tenga en cuenta que si realmente descartamos los elementos de datos de la fila anterior, acortaríamos la lista de elementos de la fila anterior aproximadamente a la misma velocidad a medida que crece la lista de la fila actual. Así la complejidad espacial permanecerá $$$O (w)$. Aunque el ancho puede variar, esto generalmente no es tan importante.

Punteros hacia atrás de baja energía

Entonces, encontramos el significado de la costura de baja energía, pero ¿qué hacer con esta información? Después de todo, de hecho, no nos preocupa la importancia de la energía, ¡sino la costura misma! El problema es que no hay forma de que el píxel final regrese al resto de la costura.

Esto es lo que me perdí en artículos anteriores, pero lo mismo se aplica a muchos problemas de programación dinámica. Por ejemplo, si recuerda la tarea de un ladrón de casas , encontramos el valor máximo para la cantidad de robos, pero no qué casas específicas necesitan ser robadas para obtener esta cantidad.

Representación de punteros posteriores

Respuesta general: almacenar de nuevo los punteros . En la tarea de cortar costuras, no solo necesitamos el valor de la energía de la costura en cada píxel. También necesita saber cuál de los píxeles en la fila anterior condujo a esta energía. Al almacenar esta información, podemos seguir los punteros inversos hasta la línea superior, obteniendo las coordenadas de todos los píxeles que componen la unión con la menor energía.

Primero, cree una clase para almacenar energía y apuntadores. La energía se utilizará para calcular subtareas. Dado que el puntero hacia atrás determina qué píxel en la línea anterior dio la energía actual, podemos imaginarlo simplemente como la coordenada x.

 class SeamEnergyWithBackPointer(): def __init__(self, energy, x_coordinate_in_previous_row=None): self.energy = energy self.x_coordinate_in_previous_row = x_coordinate_in_previous_row 

El resultado del cálculo para cada subtarea no será solo un número, sino una instancia de esta clase.

Almacenamiento de puntero hacia atrás

Al final, debe retroceder a lo largo de toda la altura de la imagen, siguiendo los signos inversos para restaurar la costura con la menor energía. Desafortunadamente, esto significa que necesita almacenar punteros para todos los píxeles de la imagen, no solo la línea anterior.

Para hacer esto, simplemente guardamos el resultado completo de todas las subtareas, aunque técnicamente es posible rechazar las energías numéricas de la costura de las líneas anteriores. Los resultados se almacenan en una matriz bidimensional, que se ve igual que la matriz de entrada.

Comencemos con la primera línea, que contiene solo energías de píxeles individuales. Como no hay una línea anterior, faltan todos los punteros posteriores, pero por coherencia, aún almacenaremos instancias de SeamEnergyWithBackPointers :

 seam_energies = [] # Initialize the top row of seam energies by copying over the top row of # the pixel energies. There are no back pointers in the top row. seam_energies.append([ SeamEnergyWithBackPointer(pixel_energy) for pixel_energy in pixel_energies[0] ]) 

El bucle principal funciona básicamente igual que la implementación anterior, con las siguientes diferencias:

• Los datos de la fila anterior contienen instancias de SeamEnergyWithBackPointer , por lo que al calcular el valor de la relación de recurrencia, debe buscar la energía de la costura dentro de estos objetos.
  
• Para guardar datos para el píxel actual, debe crear una nueva instancia de SeamEnergyWithBackPointer . Aquí almacenaremos la energía de costura para el píxel actual, así como la coordenada x de la línea anterior, utilizada para calcular la energía de costura actual.
  
• Al final de cada fila, en lugar de descartar los datos de la fila anterior, simplemente agregamos los datos de la fila actual a seam_energies .

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_parent_x = min( x_range, key=lambda x_i: seam_energies[y - 1][x_i].energy ) min_seam_energy = SeamEnergyWithBackPointer( pixel_energy + seam_energies[y - 1][min_parent_x].energy, min_parent_x ) seam_energies_row.append(min_seam_energy) seam_energies.append(seam_energies_row) 

Sigue las indicaciones

Ahora toda la tabla de subtareas está llena y podemos restaurar la costura con la menor energía. Comenzamos buscando la coordenada x en la línea inferior, que corresponde a la articulación con la menor energía:

 # Find the x coordinate with minimal seam energy in the bottom row. min_seam_end_x = min( range(len(seam_energies[-1])), key=lambda x: seam_energies[-1][x].energy ) 

Ahora ve desde la parte inferior de la imagen hacia arriba, cambiando $$$y$de len(seam_energies) - 1 a cero. En cada iteración, agregue el par actual $$$(x, y)$a la lista que representa nuestra costura, y luego establece el valor $$$x$para el objeto al que apunta SeamEnergyWithBackPointer en la fila actual.

 # Follow the back pointers to form a list of coordinates that form the # lowest-energy seam. seam = [] seam_point_x = min_seam_end_x for y in range(len(seam_energies) - 1, -1, -1): seam.append((seam_point_x, y)) seam_point_x = \ seam_energies[y][seam_point_x].x_coordinate_in_previous_row seam.reverse() 

Por lo tanto, la costura se construye hacia arriba, la lista se puede leer en orden inverso, si necesita coordenadas de arriba a abajo.

Complejidad espacial y temporal.

La complejidad del tiempo es similar a la anterior, porque todavía necesitamos procesar cada píxel una vez. Después de mirar la última línea y encontrar la articulación con la menor energía, subimos toda la altura de la imagen para restaurar la articulación. Entonces para la imagen $$$W × H$la complejidad del tiempo es igual $$$O (W × H + W + H)$.

En cuanto al volumen, aún conservamos una cantidad constante de datos para cada subtarea, pero ahora no descartamos ningún dato. Entonces usamos volumen $$$O (ancho × alto)$.

Eliminación de costuras de baja energía.

Tan pronto como se encuentre la unión vertical con la energía más baja, simplemente podemos copiar los píxeles de la imagen original a una nueva. Cada línea de la nueva imagen contiene todos los píxeles de la línea correspondiente de la imagen original, con la excepción del píxel de la costura con la energía más baja. Como eliminamos un píxel en cada fila, comenzando desde la imagen $$$W × H$entonces obtenemos la imagen $$$(W - 1) × H$.

Podemos repetir este proceso contando la función de energía en la nueva imagen y encontrando la costura de menor energía en ella. Parece tentador encontrar más de una costura de baja energía en la imagen original y luego eliminarlas todas a la vez. El problema es que las dos costuras pueden cruzarse. Cuando se elimina el primero, el segundo dejará de ser válido porque faltan uno o más píxeles.


Animación del proceso de remoción de costuras. Es mejor mirar en pantalla completa para una vista más clara de las costuras.

Cada cuadro del video es una imagen en cada iteración con visualización superpuesta de la costura con la menor energía.

Otro ejemplo

El artículo tenía muchas explicaciones detalladas, ¡así que terminemos con una serie de hermosas fotos! La siguiente foto muestra una formación rocosa en el Parque Nacional Arches:


Formación rocosa con un agujero en el Parque Nacional Arches. Foto: Mike Goad en Flickr

Función de energía para esta imagen:


La energía de cada píxel en la foto: cuanto más claro, más alto es. Presta atención a la alta energía alrededor del borde del hoyo.

Como resultado del cálculo, se obtiene una costura con la energía más baja. Tenga en cuenta que pasa a través de la roca a la derecha, entrando directamente en la formación rocosa donde la parte iluminada en la parte superior de la roca coincide con el color del cielo. ¡Quizás deberías elegir una mejor función energética!


La costura de menor energía encontrada en la imagen se muestra con una línea roja de cinco píxeles de ancho para visibilidad, aunque en realidad la costura tiene solo un píxel de ancho.

Finalmente, la imagen del arco después de cambiar el tamaño:


Arco después de la compresión a 1024 píxeles

El resultado definitivamente no es perfecto: muchos bordes de la montaña de la imagen original están distorsionados. Una de las mejoras puede ser la implementación de una de las otras funciones energéticas enumeradas en el artículo científico.

---

Aunque la programación dinámica generalmente se discute en teoría, es un método práctico útil para resolver problemas complejos. En este artículo, examinamos una de las aplicaciones de la programación dinámica: cambiar el tamaño de las imágenes para adaptarlas al contenido cortando costuras.

Aplicamos los mismos principios de dividir un problema en subtareas más pequeñas, analizando las dependencias entre estas subtareas y luego resolviendo las subtareas en un orden que minimiza la complejidad espacial y temporal del algoritmo. Además, estudiamos el uso de punteros inversos para no solo encontrar el valor de energía para la costura óptima, sino también para determinar las coordenadas de cada píxel que conformaba este valor. Luego aplicamos estas partes a un problema real, que requiere un procesamiento previo y posterior para un uso verdaderamente efectivo del algoritmo de programación dinámica.