En la escuela, cuando resolvimos ecuaciones o consideramos fórmulas, intentamos reducirlas primero varias veces, por ejemplo, Z = X - (Y + X) reduce a Z = -Y . En los compiladores modernos, este es un subconjunto de las llamadas optimizaciones de mirilla, en las que, en términos generales, un conjunto de patrones reducimos expresiones, reemplazamos instrucciones por otras más rápidas para un procesador en particular, etc. En este artículo, he compilado una colección de tales optimizaciones que se encontraron en las fuentes LLVM, GCC y .NET Core (CoreCLR).
Comencemos con ejemplos simples:
X * 1 => X -X * -Y => X * Y -(X - Y) => Y - XX * Z - Y * Z => Z * (X - Y)
verifique el último ejemplo en C ++ y en C #:
int Test(int x, int y, int z) { return x * z - y * z;
y mire el ensamblador de Clang (LLVM), GCC, MSVC y .NET Core:

Los tres compiladores de C ++ (GCC, Clang y MSVC) redujeron una multiplicación (solo vemos una instrucción imul ). C # no hizo esto con RyuJIT, pero no se apresure a regañarlo por eso, es solo que esta clase de optimizaciones está disponible en una composición limitada allí. Para hacerle entender, la implementación de toda la transformación InstCombine en LLVM requiere más de 30k líneas de código (+ 20k líneas en DAGCombiner.cpp), además, esta transformación a menudo causa una larga compilación. Por cierto, el sitio responsable de esta optimización está allí. GCC tiene un DSL especial que describe el agujero de optimización, aquí hay un fragmento ).
Decidí, por el bien del artículo, intentar implementar esta optimización en C # JIT (sostenga mi cerveza):
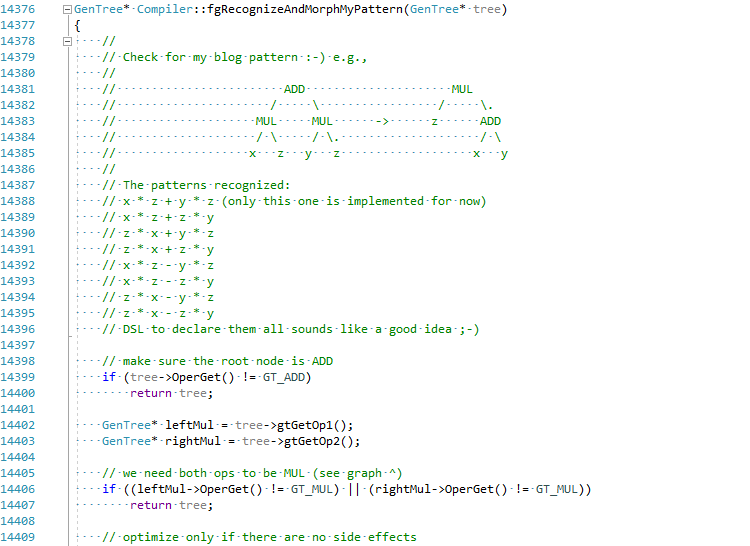
La confirmación completa se puede ver aquí EgorBo / coreclr . Veamos mi mejora ahora (en Visual Studio 2019 + Disasmo:
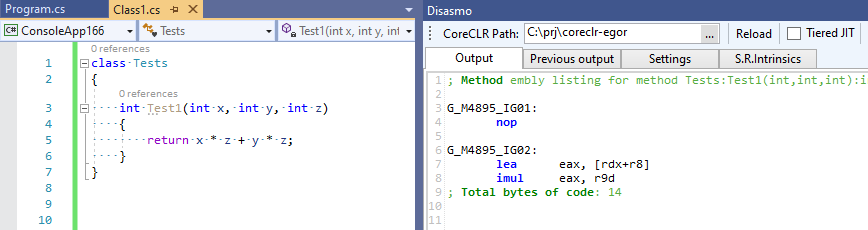
Funciona! lea + imul lugar de imul , imul y add .
Volvamos a C ++ y rastreemos esta optimización en Clang. Para hacer esto, solicite a clang que nos dé el IR LLVM inicial a través de -emit-llvm -g0 , y luego se lo entregue a LLVM al optimizador, usando los -O2 -print-before-all -print-after-all para capturar el momento exacto de la transformación elimina la multiplicación del conjunto -O2 (todo esto se puede ver en el maravilloso recurso godbolt.org ):
; *** IR Dump Before Combine redundant instructions *** define dso_local i32 @_Z5Case1iii(i32, i32, i32) { %4 = mul nsw i32 %0, %2 %5 = mul nsw i32 %1, %2 %6 = sub nsw i32 %4, %5 ret i32 %6 } ; *** IR Dump After Combine redundant instructions *** define dso_local i32 @_Z5Case1iii(i32, i32, i32) { %4 = sub i32 %0, %1 %5 = mul i32 %4, %2 ret i32 %5 }
También puede divertirse en godbolt con las herramientas LLVM: opt (optimizador) y llc (para compilar LLVM IR en asm):

De vuelta a los ejemplos. Encontré este muy buen ejemplo en GCC.
X == C - X => false if C is odd
Y es cierto: si 4 == 8 - 4 . Pero si en lugar de 8 escribe uno extraño, entonces no puede encontrar una X tal que se cumpla la igualdad:
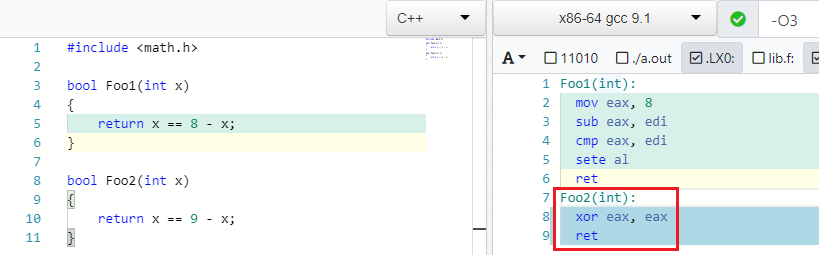
IEEE754 contraataca
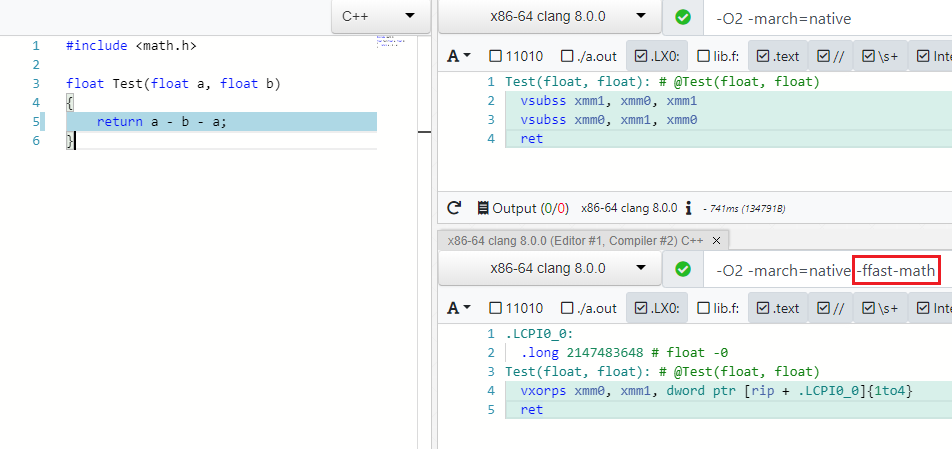
Muchas optimizaciones funcionan para diferentes tipos de datos, por ejemplo, byte , int , unsigned , float , double . Con este último, las cosas no son tan simples y las optimizaciones son manejadas por la especificación IEEE754, que se volverá loca si reduce A - B - A a -B o (A * B) * C reorganiza a A * (B * C) t. a. Las operaciones no son asociativas. Pero hay un modo especial en los compiladores modernos que le permite descuidar las especificaciones y los valores límite (NaN, + -Inf, + -0.0) en tales casos y realizar optimizaciones de forma segura: esta es Fast Math (mi solicitud de PR para agregar dicho modo a C # se puede encontrar aquí )
Como puede ver en -ffast-math no hay más dos vsubss :
Además de las expresiones, los optimizadores también tienen en cuenta el malabarismo con las funciones matemáticas de math.h , por ejemplo, el producto de los módulos del número X es igual al producto del número X:
abs(X) * abs(X) => X * X
La raíz cuadrada siempre es positiva:
sqrt(X) < Y => false, if Y is negative. sqrt(X) < 0 => false
¿Por qué calcular la raíz, si es posible en la etapa de compilación calcular el cuadrado de la constante a la derecha?
sqrt(X) > C => X > C * C

Más operaciones de root:
sqrt(X) == sqrt(Y) => X == Y sqrt(X) * sqrt(X) => X sqrt(X) * sqrt(Y) => sqrt(X * Y) logN(sqrt(X)) => 0.5*logN(X)
Un poco más de matemática escolar:
expN(X) * expN(Y) -> expN(X + Y)
Y mi optimización favorita:
sin(X) / cos(X) => tan(X)

Muchas operaciones aburridas de bits y booleanos:
((a ^ b) | a) -> (a | b) (a & ~b) | (a ^ b) --> a ^ b ((a ^ b) | a) -> (a | b) (X & ~Y) |^+ (~X & Y) -> X ^ Y A - (A & B) into ~B & A X <= Y - 1 equals to X < Y A < B || A >= B -> true ... !
Optimizaciones de bajo nivel
Hay un conjunto de optimizaciones que a primera vista no tienen sentido con matemáticos, pero son más amigables con el hierro.
X / 2 => X * 0.5
reemplazar división por multiplicación:

La operación de multiplicación de flota generalmente tiene mejores características de latencia / rendimiento que la división. Por ejemplo, aquí están las opciones para Intel Haswell:

En el modo matemático no rápido, solo se puede usar si la constante es una potencia de dos.
Por cierto, recientemente intenté agregar dicha optimización en C #. Es decir si, por ejemplo, necesita abrir un archivo con un modelo 3D y reducir todas las coordenadas 10 veces, entonces * 0.1 manejará esto 20-100% más rápido, lo que puede ser significativo.
La misma razón para:
X * 2 => X + X
Comparar con cero ( test ) es mejor que comparar con la unidad ( cmp ): mi PR para más detalles es dotnet / coreclr # 25458 :
X >= 1 => X > 0 X < 1 => X <= 0 X <= -1 => X >= 0 X > -1 => X >= 0
Y como te gusta esto:
pow(X, 0.5) => sqrt(x) pow(X, 0.25) => sqrt(sqrt(X)) pow(X, 2) => X * X ; 1 mul pow(X, 3) => X * X * X ; 2 mul

¿Qué piensas, cuántas operaciones de multiplicación necesitas para contar mod(X, 4) o X * X * X * X ?
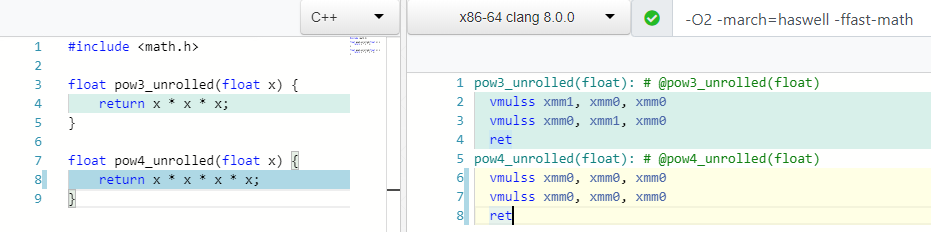
Dos! Además de calcular el 3er grado, y en el caso 4 usamos solo un registro xmm0 .
Muchos procesadores admiten una instrucción especial (FMA), que le permite realizar multiplicaciones y sumas a la vez, manteniendo la precisión durante la multiplicación:
X * Y + Z => fmadd(X, Y, Z)

Dos de mis ejemplos favoritos más son doblar algunos algoritmos en una sola instrucción (si el procesador lo admite):
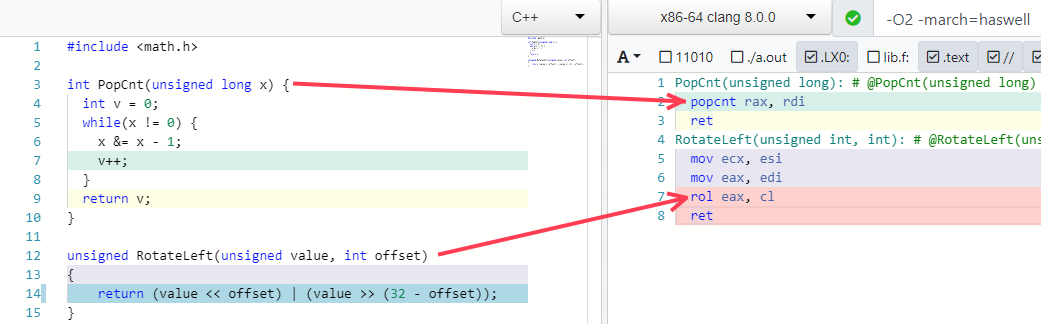
Trampas de optimización
Creo que todos entienden que no puedes apresurarte y reducir las expresiones por tres razones:
- Puede romper el código en algunos valores límite, desbordamiento, efectos secundarios ocultos, etc. ... Bugzilla LLVM contiene muchos errores de InstCombine.
- Idealmente, las optimizaciones deberían funcionar juntas en una secuencia específica.
- La expresión o partes de ella que desea reducir se pueden usar en otros lugares y su reducción conducirá a la degradación del rendimiento.
Veamos un ejemplo para el último párrafo (espiado en el artículo Direcciones futuras para la optimización de compiladores ).
Imagina que tenemos este código:
int Foo1(int a, int b) { int na = -a; int nb = -b; return na + nb; }
necesitamos hacer tres operaciones: 0 - a , 0 - b , y na + nb . Pero el optimizador para nosotros reduce esto a dos - return -(a + b); :
define dso_local i32 @_Z4Foo1ii(i32, i32) { %3 = add i32 %0, %1 ; a + b %4 = sub i32 0, %3 ; 0 - %3 ret i32 %4 }
Ahora imagine que necesitamos escribir valores intermedios na y nb en variables globales:
int x, y; int Foo2(int a, int b) { int na = -a; int nb = -b; x = na; y = nb; return na + nb; }
El optimizador aún encuentra este patrón y elimina las operaciones innecesarias (desde su punto de vista) 0 - b , ¡pero de hecho resulta que son necesarias! ¡Escribimos los resultados de estas operaciones "innecesarias" en variables globales! Esto lleva a este código:
define dso_local i32 @_Z4Foo2ii(i32, i32) { %3 = sub nsw i32 0, %0 ; 0 - a %4 = sub nsw i32 0, %1 ; 0 - b store i32 %3, i32* @x, align 4, !tbaa !2 store i32 %4, i32* @y, align 4, !tbaa !2 %5 = add i32 %0, %1 ; a + b %6 = sub i32 0, %5 ; 0 - %5 ret i32 %6 }
¡Cuatro operaciones matemáticas en lugar de tres! Nuestro optimizador nos falló y no estaba convencido de que alguien aún necesitara las expresiones intermedias que optimizó. Ahora echemos un vistazo a la salida de C # RuyJIT, en el que no existe tal optimización inteligente:
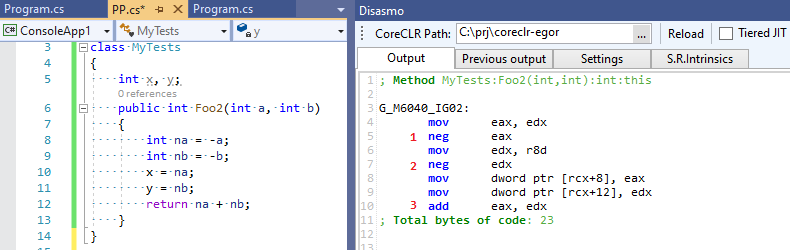
Tres operaciones en lugar de cuatro: ¡C # resultó ser más rápido que C ++ :-)!
¿Se necesitan tales optimizaciones?
Nunca se sabe cómo se verá el código después de que el compilador incorpore todo lo que puede y hace un plegado constante, propagación de copia, CSE, etc. - Se abrirá una imagen completamente diferente para él. LLVM IR y .NET IL no están vinculados a un lenguaje de programación específico, y no puede estar seguro de que un PL específico / nuevo pueda traducirse efectivamente a IR. Bueno, ¿por qué hablar al respecto si puede probar el rendimiento de InstCombine de forma intermitente en una aplicación específica ;-). Es poco probable que sea una diferencia impresionante, pero quién sabe.
¿Qué hay de C #?
Como dije, las optimizaciones de las expresiones que examinamos están muy probablemente ausentes en C #. Pero cuando digo C # quiero decir que el tiempo de ejecución más popular es CoreCLR y RyuJIT. Pero además de CoreCLR hay otros tiempos de ejecución, incluidos los que usan LLVM como backend: Mono (vea mi tweet ), Unity Burst, IL2CPP (a través de clang) y LILLC: aquí puede comparar de manera segura los resultados de C ++ con clang. Los chicos de Unity incluso reescriben el código interno de C ++ en C # sin ninguna pérdida de rendimiento, ¡ prueba !
Aquí hay algunos pipholes de optimización que se pueden encontrar en el archivo morph.cpp en el código fuente de morph.cpp de los comentarios (claramente hay un poco más):
*(&X) => X X % 1 => 0 X / 1 => X X % Y => X - (X / Y) * Y X ^ -1 => ~x X >= 1 => X > 0 X < 1 => X <= 0 X + 1 == C2 => X == C2 - C1 ((X + C1) + C2) => (X + (C1 + C2)) ((X + C1) + (Y + C2)) => ((X + Y) + (C1 + C2))
Se pueden encontrar algunos más en lowering.cpp (bajo nivel), pero en general RyuJIT obviamente pierde aquí a los compiladores de C ++. RyuJIT tiene prioridades ligeramente diferentes: antes del advenimiento de la compilación de niveles, necesitaba proporcionar una velocidad de compilación aceptable, lo que hace muy bien a diferencia de los compiladores de C ++ (recuerde sobre el pase InstCombine de 30 líneas en LLVM y lea la publicación interesante en general " "Lamentaciones modernas de C ++" ) y es mucho más útil desarrollar optimizaciones en el campo de la desvirtualización de llamadas, la eliminación del boxeo y las asignaciones (la misma Asignación de pila de objetos ); obviamente, todo esto es mucho más importante que minimizar las divisiones de seno a coseno por tangente.
Quizás con el advenimiento de la compilación de niveles, con el tiempo habrá muchas optimizaciones nuevas que no son críticas para el tiempo de compilación para el nivel 1 o incluso el nivel 2. Tal vez incluso con su API de complemento y DSL: acaba de leer este artículo, en él Prathamesh Kulkarni agregó optimización de expresión en GCC en solo un par de líneas DSL:
(simplify (plus (mult (SIN @0) (SIN @0)) (mult (COS @0) (COS @0))) (if (flag_unsafe_math_optimizations)1. { build_one_cst (TREE_TYPE (@0))
para esta expresión de un libro de texto de matemáticas ;-):
cos^2(X) + sin^2(X) equals to 1
Enlaces utiles
- "Direcciones futuras para la optimización de compiladores" , Nuno P. Lopes y John Regehr
- "Cómo LLVM optimiza una función" , John Regehr
- "La sorprendente inteligencia de los compiladores modernos" , Daniel Lemire
- "Agregar optimización de mirilla a GCC" , Prathamesh Kulkarni
- "1. C ++, C # y Unity" , Lucas Meijer
- "Lamentaciones" modernas de C ++ " , Aras Pranckevičius
- "Optimizaciones de mirilla probadamente correctas con vida" , Nuno P. Lopes, David Menéndez, Santosh Nagarakatte y John Regehr