Introduccion
Uno de los primeros radiotelescopios construidos por American Grotto Reber en 1937. El radiotelescopio era un espejo de hojalata con un diámetro de 9,5 m montado en un marco de madera:

Para 1944, Reber había compilado el primer mapa de la distribución de ondas de radio espaciales en la región de la Vía Láctea.
El desarrollo de la radioastronomía conllevó una serie de descubrimientos: en 1946, se descubrió la emisión de radio de la constelación Cygnus, en 1951 - radiación extragaláctica, en 1963 - cuásares, y en 1965 se descubrió radiación de fondo relicto en una longitud de onda de 7,5 cm.
En 1963, se construyó un radiotelescopio único de 300 metros en Arecibo (Puerto Rico). Este es un recipiente inmóvil con un irradiador en movimiento, construido en una hendidura natural del terreno.

Los radiotelescopios individuales tienen una resolución angular pequeña, que está determinada por la fórmula:
T h e t a = f r a c l a m b d a d donde
l a m b d a - longitud de onda
d - diámetro del radiotelescopio.
Obviamente, para mejorar la resolución, es necesario aumentar el diámetro de la antena, que es una tarea físicamente difícil. Fue posible resolverlo con la llegada de los interferómetros de radio.
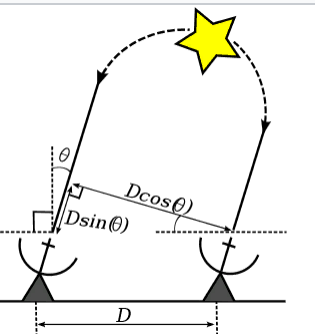
El frente de una onda electromagnética emitida por una estrella distante cerca de la Tierra puede considerarse plana. En el caso del interferómetro más simple, que consta de dos antenas, la diferencia en la trayectoria de los rayos que llegan a estas dos antenas será igual a:
D e l t a = D c d o t s i n ( T h e t a ) ,
donde:
D e l t a - la diferencia en la trayectoria de los rayos;
D - distancia entre antenas;
T h e t a - el ángulo entre la dirección de llegada de los rayos y la normal a la línea en la que se ubican las antenas.
En
T h e t a = 0 Las ondas que llegan a ambas antenas se suman en fase. En antifase, las ondas aparecerán por primera vez cuando:
Delta= frac lambda2, Theta=arcsin frac lambda2D ,
donde:
lambda - longitud de onda.
El próximo máximo será en
Delta= lambda, mínimo a
Delta= frac3 lambda2 etc. Se obtiene un patrón de radiación de múltiples pétalos (DN), cuyo ancho del lóbulo principal en
lambda<<D es igual a
lambda/D . El ancho del lóbulo principal determina la resolución angular máxima del radio interferómetro, es aproximadamente igual al ancho del lóbulo.
La radio interferometría de base ultra larga (VLBI) es un tipo de interferometría utilizada en radioastronomía en la que los elementos receptores del interferómetro (telescopios) no se encuentran más cerca que a distancias continentales entre sí.
El método VLBI le permite combinar observaciones realizadas por varios telescopios y, de este modo, simular un telescopio cuyas dimensiones son iguales a la distancia máxima entre los telescopios originales. La resolución angular del VLBI es decenas de miles de veces mayor que la resolución de los mejores instrumentos ópticos.
El estado actual de las redes VLBI
Hoy, varias redes VLBI están escuchando espacio:
- European –EVN (European VLBI Network), que consta de más de 20 radiotelescopios;
- American –VLBA (Very Long Baseline Array), que incluye diez telescopios con un diámetro de 25 metros cada uno;
- Japonés: JVN (Red VLBI japonesa) consta de diez antenas ubicadas en Japón, incluidas cuatro antenas astrométricas (proyecto VERA - Exploración VLBI de radioastrometría);
- Australiano - LBA (Long Baseline Array);
- Chino: CVN (red china VLBI), que consta de cuatro antenas;
- Corea del Sur: KVN (red coreana VLBI), que incluye tres radiotelescopios de 21 metros;
- El ruso, basado en el complejo radio interferométrico permanente, "Kvazar-KVO" con radiotelescopios con un diámetro de 32 m, equipado con crioradiómetros altamente sensibles en el rango de longitud de onda de 1.35 cm a 21 cm. La longitud de las bases - el diámetro efectivo del "espejo" sintetizado - es de aproximadamente 4400 km en la dirección este-oeste (ver foto).
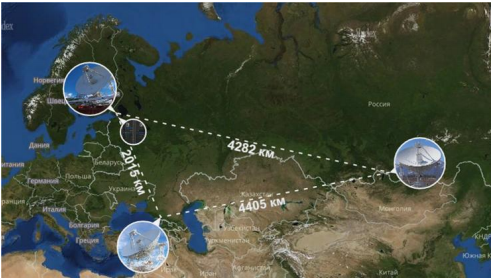
En el complejo VLBI "Kvazar-KVO", los estándares de hidrógeno se utilizan como fuente de frecuencia de referencia para todas las transformaciones de frecuencia, que utilizan la transición entre los niveles de la estructura hiperfina del estado fundamental de un átomo de hidrógeno con una frecuencia de 1420.405 MHz, correspondiente a 21 cm en radioastronomía.
Tareas resueltas mediante el VLBI
- Astrofísica Las imágenes de radio de los objetos del espacio natural (cuásares y otros objetos) se están construyendo con una resolución de décimas y centésimas de mas (milisegundos de arco).
- Estudios astrometricos. Construcción de sistemas de tiempo coordinado. Los objetos de investigación son fuentes de radio de tamaños angulares extremadamente pequeños, incluidas fuentes de radio cuasistelares y los núcleos de radiogalaxias, que, debido a su gran lejanía, son objetos casi ideales para crear una red de objetos estacionarios de soporte.
- Investigación sobre la mecánica celeste y la dinámica del sistema solar, navegación espacial. La instalación de una baliza en las superficies de los planetas y el seguimiento de las balizas de las estaciones automáticas interplanetarias permite utilizar el método VLBI para estudiar parámetros tales como el movimiento orbital del planeta, la dirección de los ejes de rotación y su precesión, la dinámica del sistema planeta-satélite. Para la Luna, el problema muy importante de determinar la libración física y determinar la dinámica de los sistemas Luna-Tierra también se está resolviendo.
Navegación en el espacio usando VLBI
- Monitoreando los movimientos de los astronautas en la superficie lunar en 1971. Se movieron con la ayuda del rover. La precisión de determinar su posición con respecto al módulo lunar alcanzó los 20 cm y dependió principalmente de la libración de la luna (Libración - oscilaciones periódicas de la luna en forma de péndulo con respecto a su centro de masa);
- Soporte de navegación para la entrega y descarga de sondas de aerostato de vehículos voladores a la atmósfera de Venus (proyecto VEGA). La distancia a Venus es de más de 100 millones de km, la potencia del transmisor es de solo 1 vatio. Los lanzamientos de VEGA-1/2 tuvieron lugar en diciembre de 1984. Los globos fueron arrojados a la atmósfera de Venus el 11 y 15 de junio de 1985. La observación se llevó a cabo durante 46 horas.
Diagrama estructural de una red VLBI simplificada
Basado en una red VLBI real, utilizando el software Python, modelamos un sistema VLBI simplificado en forma de modelos separados para cada unidad o proceso. Este conjunto de modelos será suficiente para observar los procesos básicos. El diagrama estructural de una red VLBI simplificada se presenta en la figura:
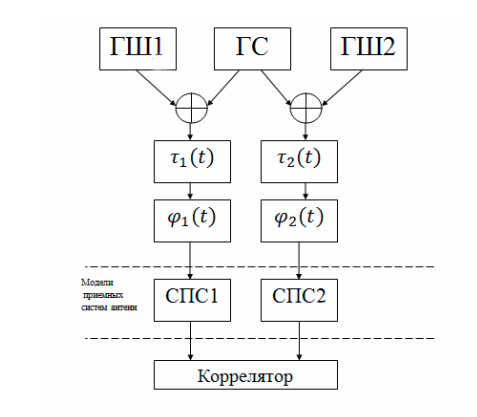
El sistema incluye los siguientes componentes:
- generador de señal de fase modulada útil (HS);
- generadores de ruido (GSh1, GSh2). El sistema tiene dos radiotelescopios (antenas receptoras) que tienen su propio ruido. Además, hay ruidos de la atmósfera y otras fuentes naturales y artificiales de emisión de radio;
- una unidad de retraso de tiempo que simula un retraso de tiempo linealmente variable debido a la rotación de la Tierra;
- desplazador de fase que simula el efecto Doppler;
- sistema de conversión de señal (SPS), que consiste en un oscilador local, para transferir la señal hacia abajo en frecuencia, y un filtro de paso de banda;
- Correlacionador FX
El circuito correlacionador se muestra en la siguiente figura:
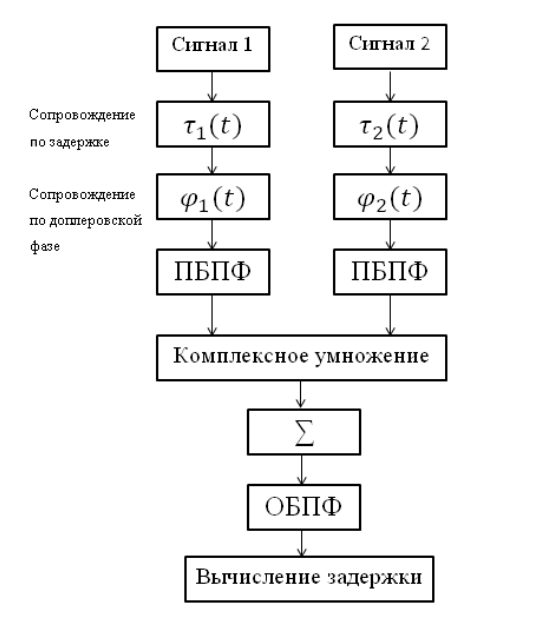
El circuito correlacionador dado, que incluye los siguientes bloques:
- transformada de Fourier rápida directa (PBPF) y transformada de Fourier inversa (OBPF);
- compensar el retraso introducido anteriormente;
- efecto compensador Doppler;
- multiplicación compleja de dos espectros;
- sumando implementaciones acumuladas.
Modelo de señal de navegación
Lo más conveniente para las mediciones de VLBI son las señales de navegación de la nave espacial de los sistemas de navegación por satélite, como GPS y GLONASS. Se imponen varios requisitos a las señales de navegación:
- le permite definir bien el pseudorango;
- transmitir información sobre la posición del sistema de navegación;
- ser distinguible de las señales de otros NS;
- No interfiera con otros sistemas de radio;
- No requiere equipos complejos para recibir y transmitir.
En una medida suficiente, están satisfechos con una señal con una modulación de fase binaria (dos posiciones): BPSK (tecla de cambio de fase binaria), que en la literatura rusa se denomina FM-2. Esta modulación cambia la fase de la oscilación de la portadora por π, que se puede representar como:
S(t)=A cdotG(t) cdotcos(2 pift),donde G (t) es la función de modulación.
Para implementar la modulación de fase, se pueden usar dos generadores, cada uno de los cuales forma la misma frecuencia, pero con una fase inicial diferente. La función de modulación le permite ampliar el espectro de la señal y medir con precisión el pseudorango (la distancia entre el satélite y el receptor, calculada por el tiempo de propagación de la señal sin corrección por la diferencia entre el reloj del satélite y el receptor).
Aquí hay una lista que explica los principios básicos de BPSK:
Listadofrom scipy import* from pylab import* import numpy as np import scaleogram as scg f = 2;
Obtenemos:
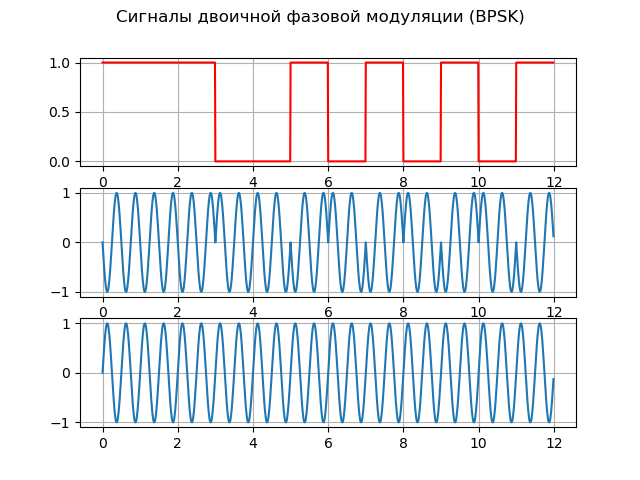
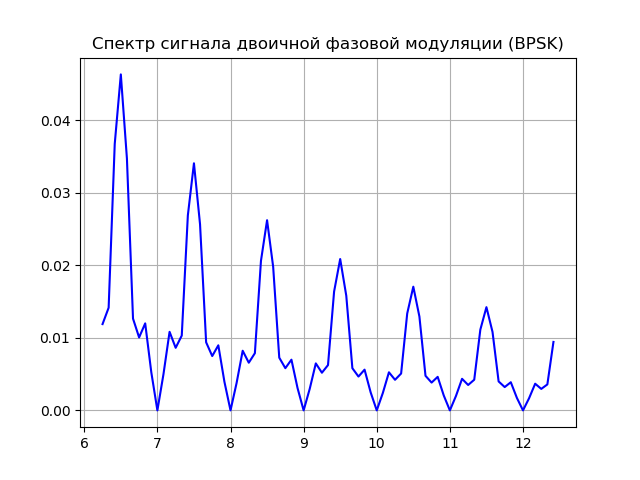
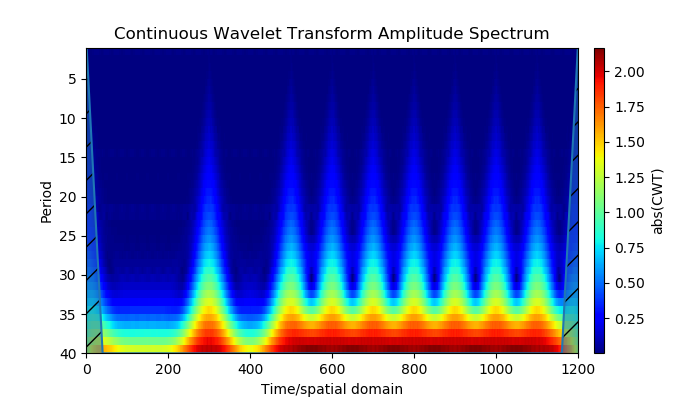
Modelo fuente
La señal armónica de navegación modulada en fase de un satélite o nave espacial tiene la forma:
x=a(2 pifct+ sumsncos(2 pifnt)),donde esta la frecuencia portadora
fc=$8. GHz
La señal tiene varios parámetros controlados: la amplitud de la enésima oscilación moduladora
sn, su frecuencia
fc y la amplitud de la oscilación portadora a.
Para obtener una función de correlación en la que se suprimen sus lóbulos laterales tanto como sea posible y se alcanza el pico de correlación más estrecho, variaremos los valores de frecuencia utilizando los valores de 2, 4, 8 y 16 MHz, y el índice de modulación en el rango de 0 a 2π en incrementos de π. Permítame darle una lista del programa para dicha búsqueda de parámetros de una función modulada en fase para el resultado final:
Obtenemos:
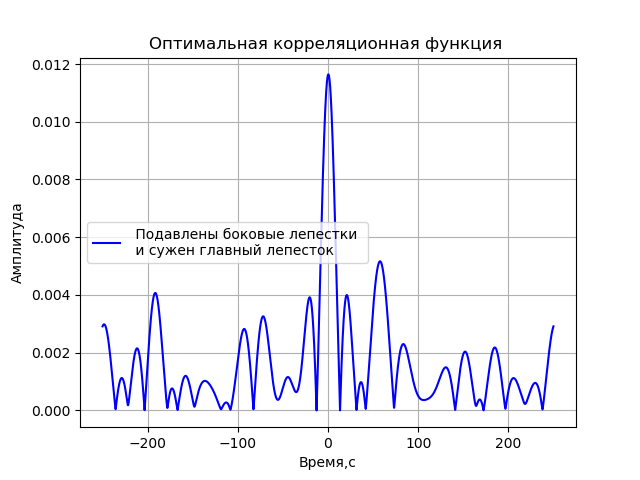
La función resultante tiene la forma:
x=cos(2 pifct+2 picos(2 pi106t)+2 picos(2 pi108t)+4 picos(2 pi1016t)).(1)Además, esta función se utilizará para simular VLBI.
Modelo de un generador de ruido que simula la interferencia recibida junto con una señal del espacio y de la atmósfera de la Tierra
La función (1) de la señal de navegación modulada en fase se puede aplicar a ambos canales del radio interferómetro, pero es necesario tener en cuenta el retraso de la señal en el segundo canal y el ruido en ambos canales como se muestra en la siguiente lista:
Obtenemos:
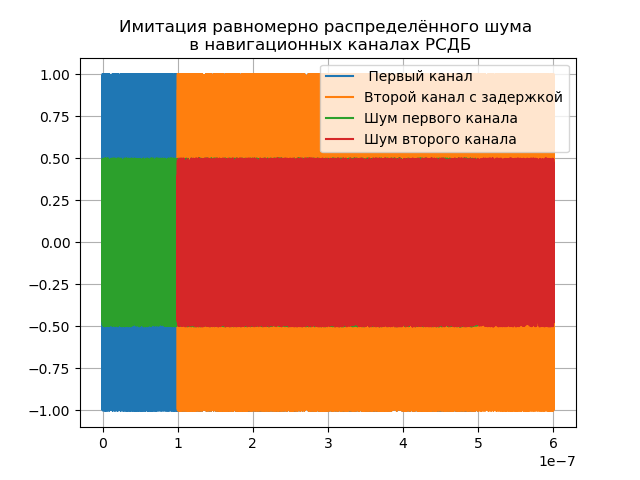
El delay delay = 1e-7 está configurado para demostración, en realidad depende de la base y puede alcanzar cuatro o más unidades.
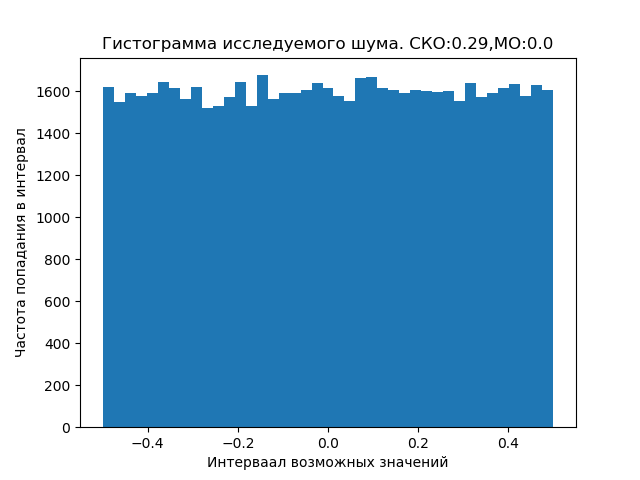
Los ruidos tanto cósmicos como cercanos a la Tierra se pueden distribuir de acuerdo con una ley diferente del uniforme dado, que requiere estudios especiales.
Modelando el efecto Doppler
Debido al hecho de que la Tierra tiene una forma redondeada y gira alrededor de su eje, las señales del espacio llegan a las antenas con diferentes retrasos. Por esta razón, es necesario cambiar las señales a tiempo y tener en cuenta la frecuencia Doppler. Consideraremos aproximadamente que la demora varía de acuerdo con una ley lineal:
taux(t)=ax+bxt,(2)donde
ax=1..3 cdot10−3 ms, y
bx=1..3 cdot10−6 ms La fase Doppler se encuentra como una derivada del retraso:
fdx= fracd tau(t)dt=bx,(3)La señal recibida debería verse así:
hatx=x(t− taux)ej2 pifdxt,donde x (t) es la señal radiada de la nave espacial.
En la siguiente lista se muestra una demostración del efecto Doppler:
Obtenemos:
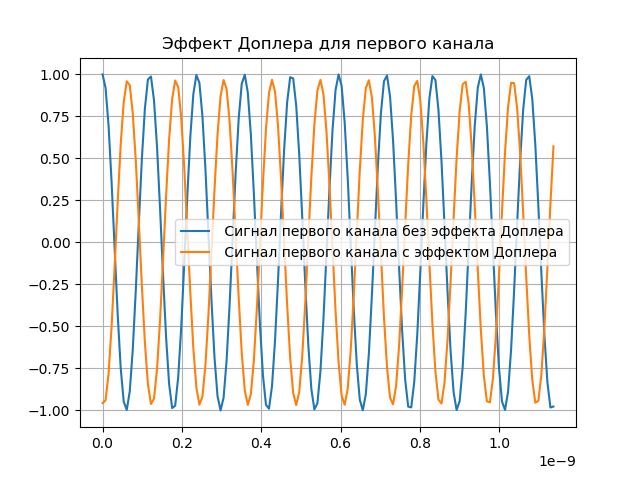
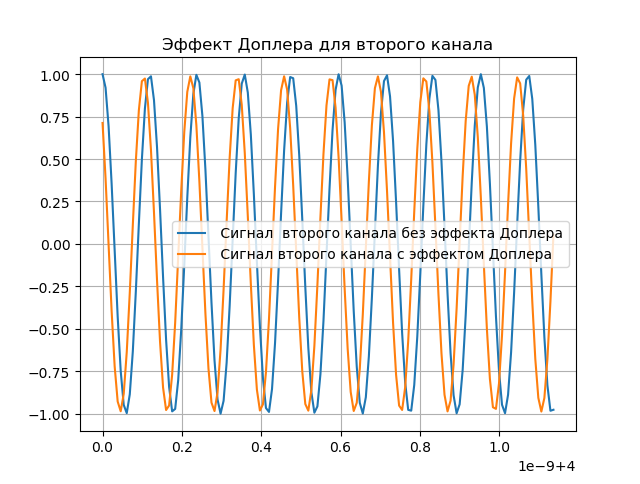
Compensación Doppler de modelado
Obviamente, los cambios realizados en la señal deben ser compensados. Para este propósito, el sistema contiene soporte para el retraso y la fase Doppler. Después de que la señal pasa a través del sistema de registro, se introduce un retraso:
tauex(t)=ax+bext,(4)Considerará que el retraso se calcula con cierta precisión, de modo que
left|aex−ax right|<30 ns
left|bex−bx right|<10 ns, es decir Será un poco diferente de lo que hizo retrasos anteriores. Está claro que el retraso se introduce con el signo opuesto al introducido anteriormente.
La señal recibida se verá así:
hatx= tildex(t+ tauex)e−j2 pifdet.(5)La compensación del efecto Doppler se muestra en el siguiente listado:
Obtenemos:
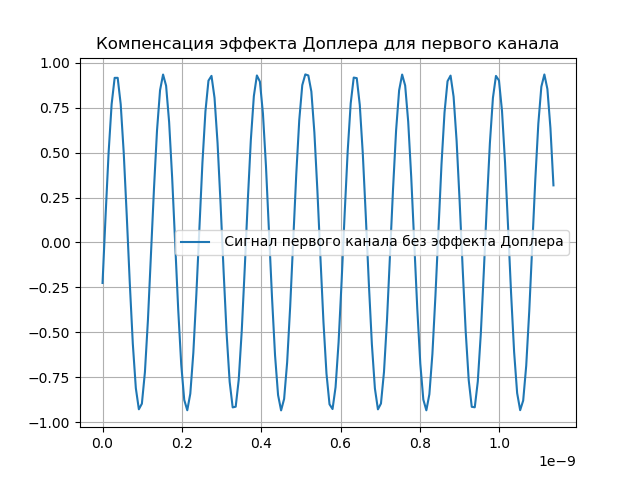
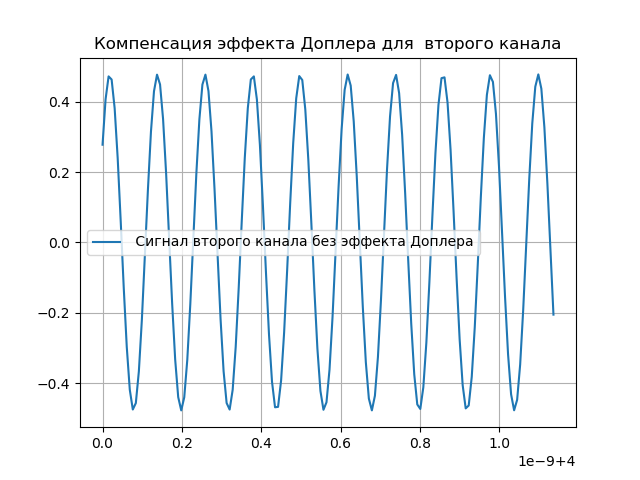
Señal de simulación heterodina
Después de que la señal ingresa al sistema de registro, se produce una conversión de frecuencia, que también se denomina heterodino. Esta es una transformación no lineal en la cual de las señales de dos frecuencias diferentes
f1 y
f2 la señal de frecuencia de diferencia se resalta
f= left|f1−f2 right.|$ La frecuencia de la señal del oscilador local será igual a la diferencia entre la frecuencia de la señal investigada y la frecuencia que desea obtener después de la transferencia. El heterodino se lleva a cabo utilizando un generador auxiliar de oscilaciones armónicas: un oscilador local y un elemento no lineal. Matemáticamente, heterodyning es la multiplicación de una señal por un exponente:
xg= hatxej2 pifgt,(6)donde
fg - señal del oscilador local.
Programa para heterodyning:
Obtenemos:
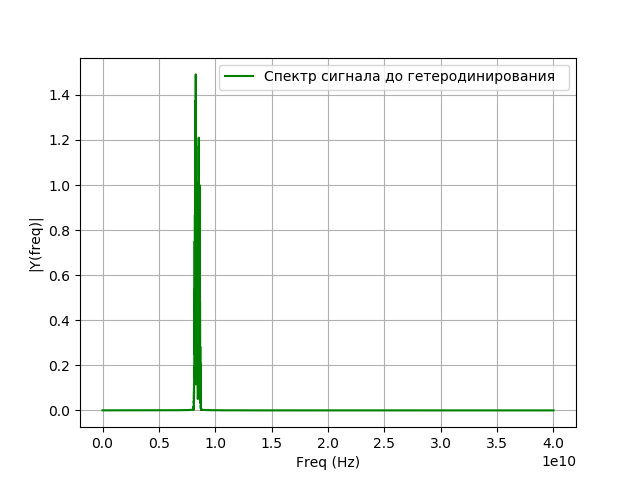
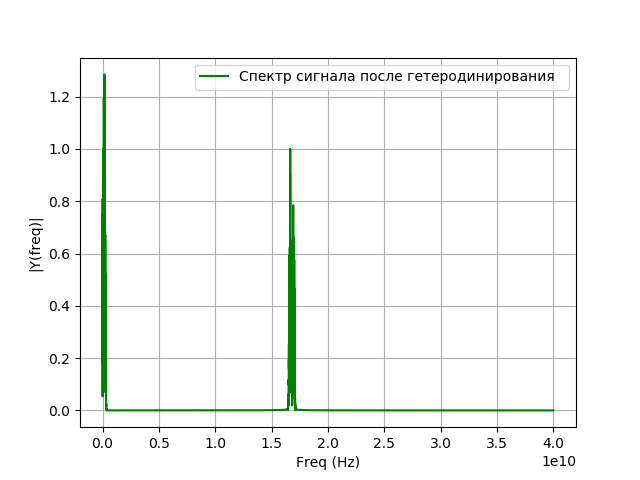
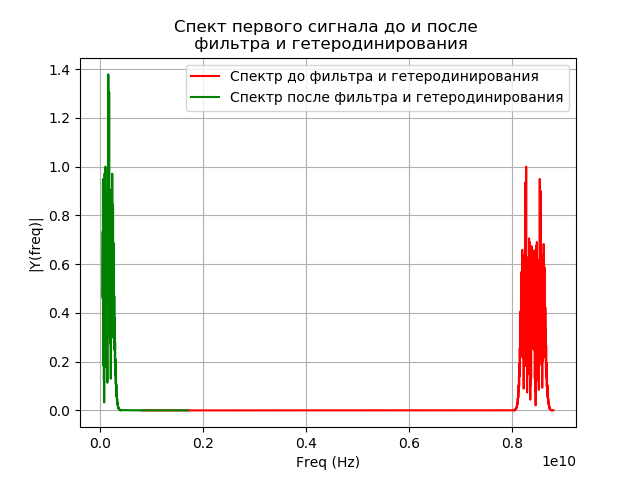
Modelado de filtrado de señal después de heterodino
Después de heterodinar, la señal entra al filtro de paso de banda. Banda de paso de filtro (PP)
fpass=32 MHz La respuesta de impulso del filtro se calcula mediante el método de ventana utilizando la función de biblioteca signal.firwin. Para obtener una señal en la salida del filtro, se realiza la convolución del filtro y la señal en el dominio del tiempo. La integral de convolución para nuestro caso toma la forma:
checkx(t)= int+ infty− inftyxg(t)h(t−t′)dt,(7)donde h (t) es la respuesta al impulso del filtro.
La convolución se encuentra usando la función de biblioteca signal.convolve. La señal registrada, teniendo en cuenta la heterodinación y el filtrado, se presenta en forma de fórmula
checkx(t)=( hatx(t)e−j2 pifgt)∗hdonde la convolución se indica con *.
Programa para modelar filtración:
Obtenemos:
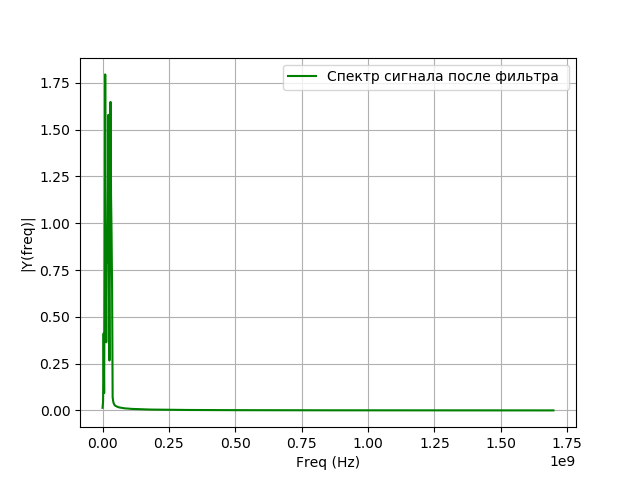
Los convertidores de señal digital para VLBI utilizan principalmente filtros con una respuesta de impulso finita (FIR), ya que tienen una serie de ventajas en comparación con los filtros con una respuesta de impulso infinito (IIR):
- Los filtros FIR pueden tener una respuesta de fase estrictamente lineal en el caso de simetría de respuesta de impulso (IM). Esto significa que al usar dicho filtro, se pueden evitar las distorsiones de fase, lo cual es especialmente importante para la radio interferometría. Los filtros con una respuesta de impulso infinita (IIR) no tienen las propiedades de simetría de ELLOS y no pueden tener una respuesta de fase lineal.
- Los filtros FIR no son recursivos, lo que significa que siempre son estables. La estabilidad de los filtros IIR no siempre se puede garantizar.
- Las consecuencias prácticas de usar un número limitado de bits para implementar filtros son significativamente menos significativas para los filtros FIR.
En la lista anterior, el modelo del filtro de paso de banda FIR se implementa utilizando el método de ventana, el orden del filtro se seleccionó de modo que la forma de la respuesta de frecuencia del filtro fuera cercana a la rectangular. El número de coeficientes del filtro simulado es n = 100001, es decir, el orden del filtro es P = 100000.
Programa para construir la respuesta de frecuencia y la respuesta de fase del filtro FIR obtenido:
Obtenemos:

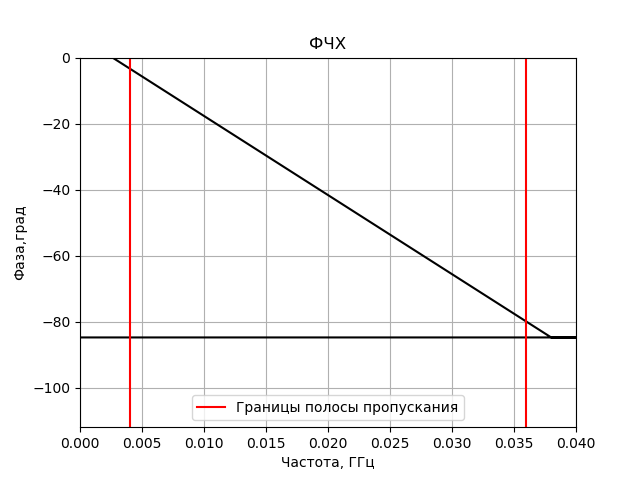
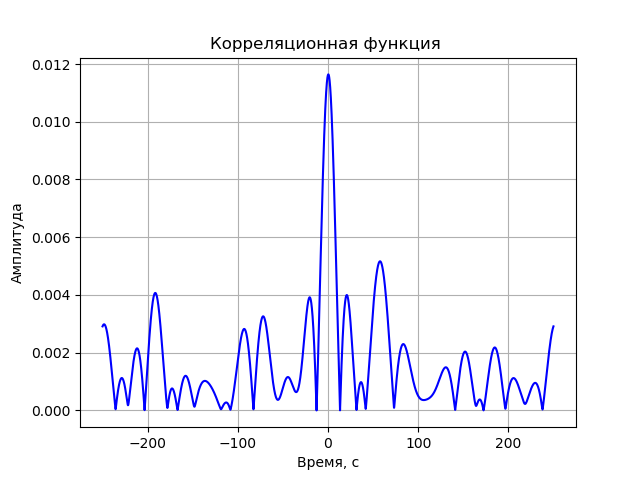
Modelo de correlacionador de efectos
A continuación, cada señal se somete a una rápida transformación de Fourier (FFT). FFT se implementa utilizando la función de biblioteca fft de scipy.fftpack. Los espectros resultantes son conjugados complejos multiplicados:
S(j omega)=S1(j omega)∗S2(j omega)=(a1+jb1)∗(a2−jb2)=a1a2+b1b2+j(b1a2−a1b2)La última acción es la inversa de la FFT. Como la amplitud de la función de correlación es de interés, la señal resultante debe convertirse mediante la fórmula:
A= sqrtre2+im2Programa para la función de correlación sin tener en cuenta las distorsiones del sistema de registro:
Obtenemos:
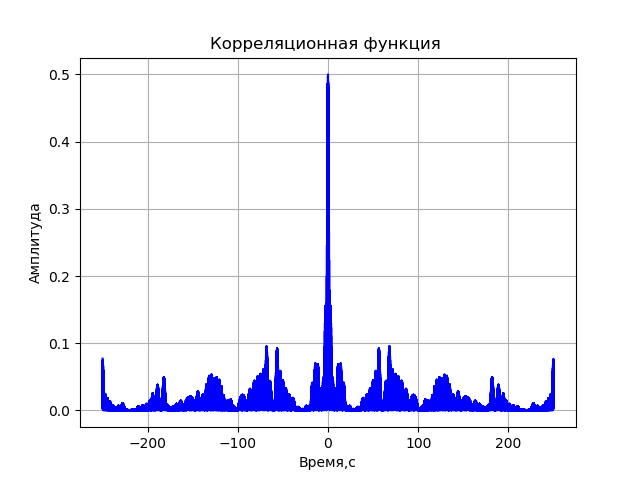
Listado completo del modelo de computadora de VLBI:
Obtenemos:
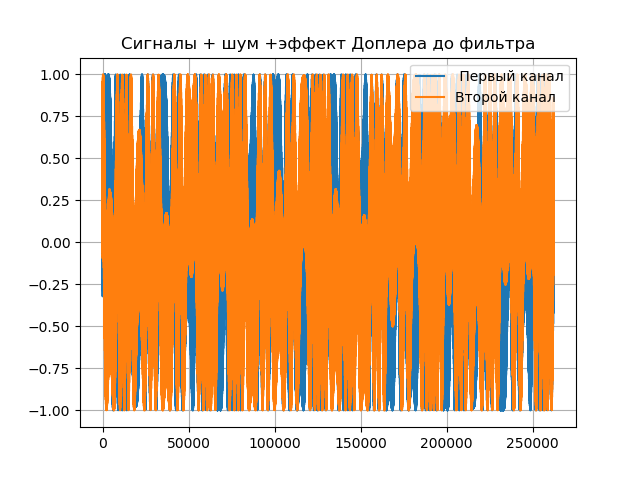

Conclusiones
- Se presenta una breve historia del desarrollo de la radioastronomía.
- Se analiza el estado actual de las redes VLBI.
- Se consideran los problemas resueltos mediante redes VLBI.
- Las herramientas de Python crearon un modelo de señales de navegación con modulación de fase binaria (dos posiciones): BPSK (tecla de cambio de fase binaria). El modelo utiliza análisis wavelet de modulación de fase.
- Se ha obtenido un modelo de fuentes de señal, que permite determinar los parámetros de modulación que proporcionan la función de correlación óptima según el criterio para suprimir los lóbulos laterales y la amplitud máxima del lóbulo central.
- Se obtiene un modelo de red VLBI simplificada, teniendo en cuenta el ruido y el efecto Doppler. Se consideran las características de filtrado utilizando un filtro con una respuesta de impulso finita.
- Después de un breve resumen de la teoría, todos los modelos están equipados con programas de demostración que le permiten rastrear la influencia de los parámetros del modelo.