La segmentación manual de los pulmones dura unos 10 minutos y requiere cierta habilidad para obtener el mismo resultado de alta calidad que con la segmentación automática. La segmentación automática tarda unos 15 segundos.
Supuse que sin una red neuronal, sería posible obtener una precisión no superior al 70%. También sugerí que las operaciones morfológicas solo están preparando una imagen para algoritmos más complejos. Pero como resultado del procesamiento de esas al menos unas 40 muestras tomográficas que están disponibles, el algoritmo seleccionó los pulmones sin errores, y después de la prueba en los primeros cinco casos, el algoritmo no experimentó cambios significativos y desde la primera aplicación funcionó correctamente en los 35 estudios restantes sin cambio ajustes
Las redes neuronales también tienen un signo negativo: para su entrenamiento necesita cientos de muestras de entrenamiento de los pulmones, que deberán etiquetarse manualmente.
Contenido
La estructura del sistema respiratorio.
El sistema respiratorio incluye las vías respiratorias y los pulmones. Asignar el tracto respiratorio superior e inferior. El punto de separación entre el tracto respiratorio superior e inferior es el punto de intersección de los canales respiratorios y alimenticios. Todo encima de la laringe es la sección superior, y el resto es inferior.
Enumeramos los órganos respiratorios:
Cavidad nasal : nariz, senos maxilares, etc.
La faringe es el canal a través del cual viajan los alimentos y el aire.
Laringe : responsable de la formación de la voz. Ubicado a nivel de las vértebras cervicales C4-C6.
Tráquea : un tubo que conecta la laringe y los bronquios.
Los bronquios son los canales respiratorios, la mayoría de los cuales se encuentran dentro de los pulmones.
Los pulmones son el principal órgano respiratorio.

Escala Hounsfield
Godfrey Hounsfield es un ingeniero eléctrico británico que, junto con el teórico estadounidense Allan Cormack, desarrolló la tomografía computarizada, por la cual recibió el Premio Nobel en 1979.

Escala de Hounsfield: una escala cuantitativa de densidad de rayos X que se mide en unidades de Hounsfield, denotada por HU.
La densidad de rayos X se calcula sobre la base del coeficiente de atenuación de la sustancia, es decir, el grado de disminución de la potencia de radiación al pasar a través de esta sustancia.
La densidad de rayos X se calcula mediante la fórmula:
$$ display $$ {μ_ {X} -μ_ {water} \ over μ_ {water} -μ_ {air}} \ times 1000 $$ display $$
donde - coeficientes de atenuación lineal para la sustancia medida, agua y aire.
La densidad de rayos X es negativa porque la densidad cero de rayos X corresponde al agua. Esto significa que todas las sustancias a través de las cuales pasan las ondas de rayos X con una disminución menor en la potencia de radiación que a través del agua (por ejemplo, tejido pulmonar, aire) tendrán una densidad de rayos X negativa.
Las siguientes son densidades aproximadas de rayos X para varios tejidos:
- Aire: -1000 HU.
- Órganos respiratorios: -950 a -300 HU.
- Sangre (sin contraste vascular): 0 a 100 HU.
- Huesos: 100 a 1000 HU.

Enlaces de Wikipedia: escala Hounsfield , Godfrey Hounsfield , coeficiente de atenuación .
Morfología matemática
El lugar principal entre los algoritmos seleccionados en este artículo está ocupado por operaciones morfológicas.
En el campo de la visión por computadora, las operaciones morfológicas llaman a un grupo de algoritmos para transformar la forma de los objetos. Muy a menudo, las operaciones morfológicas se aplican a imágenes binarizadas, donde los vóxeles de los objetos corresponden a unidades y el vacío a ceros.
Las principales operaciones morfológicas incluyen:
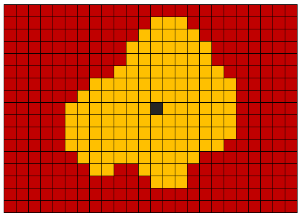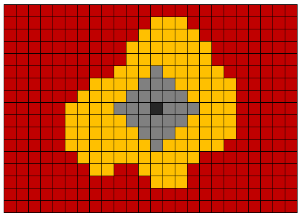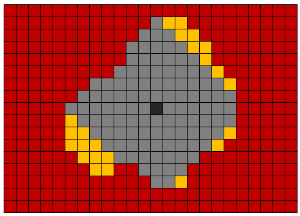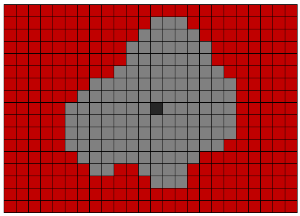
Dilatación morfológica (dilatación, expansión) : agregar nuevos vóxeles a todos los vóxeles de los bordes de los objetos. Es decir, a lo largo de todos los vóxeles de límites, se hace un pasaje con un núcleo con una forma dada (bola, cubo, cruz, etc.). Esta operación se usa a menudo para conectar muchos objetos adyacentes en un solo objeto.
Erosión morfológica (erosión, erosión) : la destrucción de todos los vóxeles que se encuentran en el borde de los objetos. Esta operación es lo opuesto a la dilatación. Esta operación es útil para eliminar el ruido en forma de muchos objetos pequeños interconectados. Sin embargo, este método de eliminación de ruido debe usarse solo si el objeto segmentado tiene un espesor significativamente mayor que el radio de erosión.
El cierre morfológico es una dilatación seguida de erosión. Se utiliza para cerrar aberturas dentro de objetos y para combinar objetos adyacentes.
La apertura morfológica (apertura) es erosión seguida de dilatación. Se utiliza para eliminar pequeños objetos de ruido y para dividir objetos en varios objetos.


Algoritmo de Lee y Compresión RLE
Para aislar objetos en un volumen de vóxeles binarizado, se utiliza el algoritmo de Lee. Este algoritmo se inventó originalmente para encontrar el camino más corto. Pero lo usamos para seleccionar y mover objetos de un conjunto tridimensional de vóxeles a otro. Su esencia es el movimiento paralelo en todas las direcciones posibles desde el punto de partida. Para el caso tridimensional, son posibles 26 o 6 direcciones de movimiento desde un vóxel dado (si el vóxel no se encuentra en el borde de la imagen).
Para optimizar la velocidad, utilizamos el algoritmo de codificación de longitud de ejecución. Su esencia radica en el hecho de que las secuencias de unos y ceros se reemplazan por un dígito igual al número de elementos en la secuencia. Por ejemplo, la cadena "00110111" se puede reemplazar como: "2; 2; 1; 3". Esto reduce el número de accesos a la memoria.

Enlaces de Wikipedia: algoritmo Lee , algoritmo RLE .
Umbral de conversión de volumen base
Usando un tomógrafo, se obtuvieron datos sobre la densidad de rayos X en cada punto del espacio. Los vóxeles de aire tienen una densidad de rayos X que varía de -1100 a -900 HU, y los vóxeles de los órganos respiratorios de -900 a -300 HU. Por lo tanto, podemos eliminar todos los vóxeles en exceso que tengan una densidad de rayos X mayor que -300 HU. Como resultado, obtenemos un volumen de vóxel binarizado que contiene solo órganos respiratorios y aire.
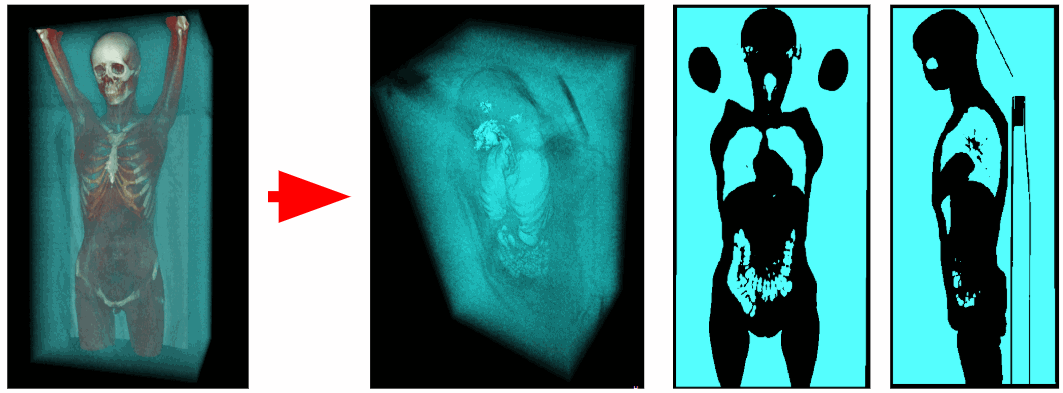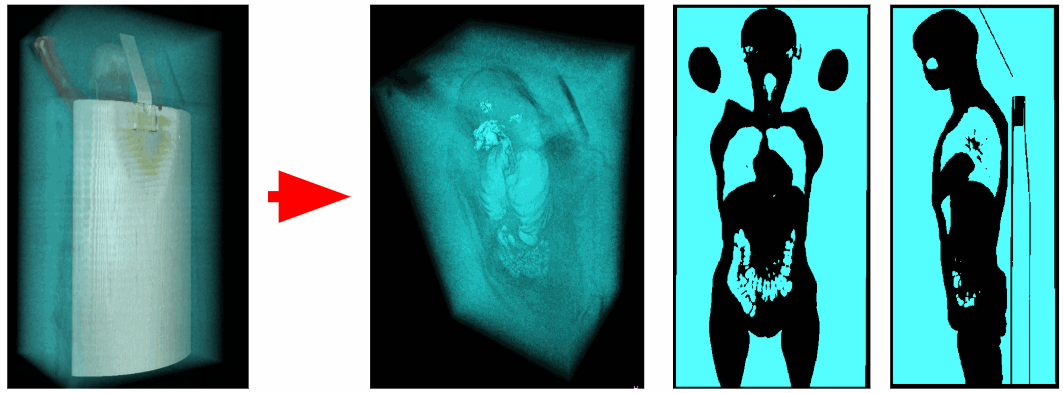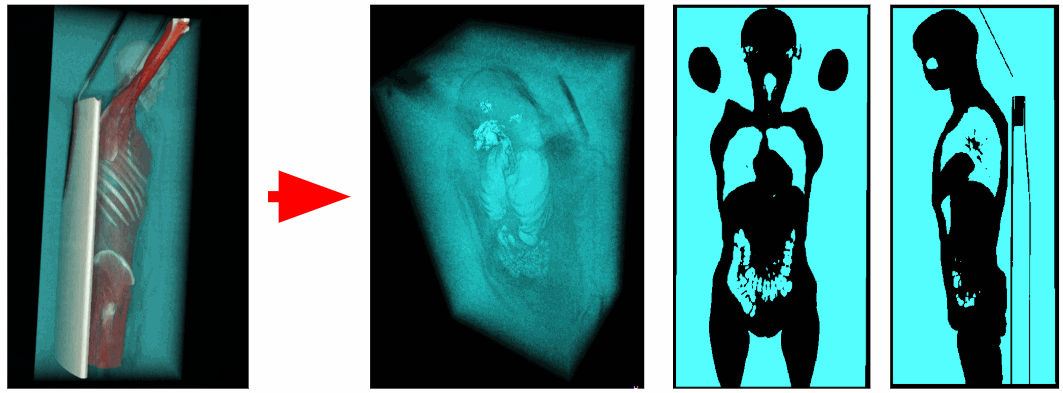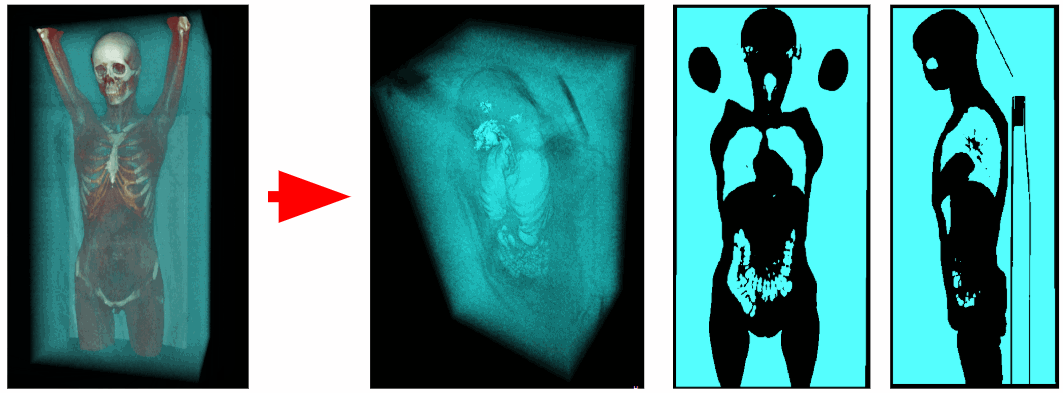
Recorte de aire externo
Para aislar el aire interno del cuerpo, eliminaremos todos los objetos adyacentes a las esquinas de la escena del vóxel. Así nos deshacemos del aire externo.

Sin embargo, no en todos los casos se eliminará el aire dentro de la mesa del tomógrafo, ya que puede no tener una conexión con las esquinas de la escena.

Por lo tanto, escanearemos no solo las esquinas, sino también todos los vóxeles que se encuentran en cualquiera de los planos fronterizos de la escena. Pero como resultado, por alguna razón, los pulmones también se fueron. Resulta que la tráquea también tenía una conexión con el plano superior de la escena.
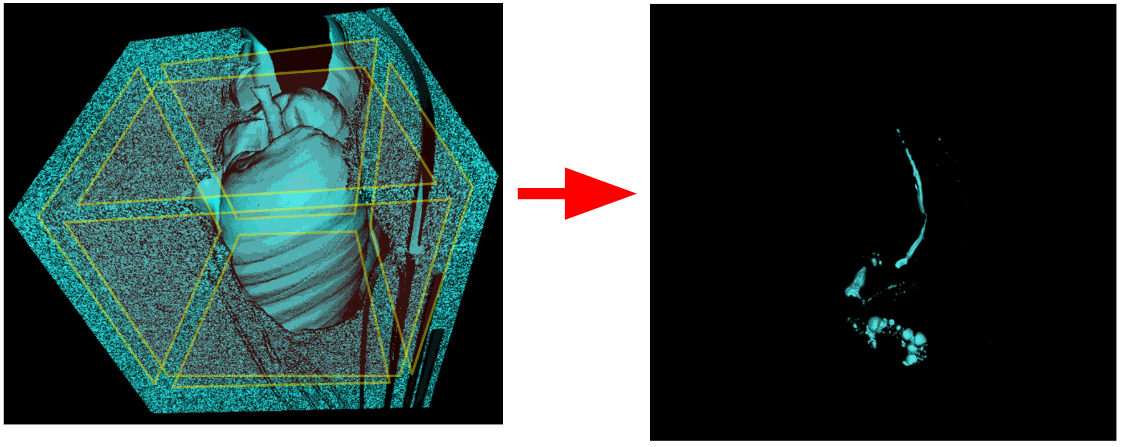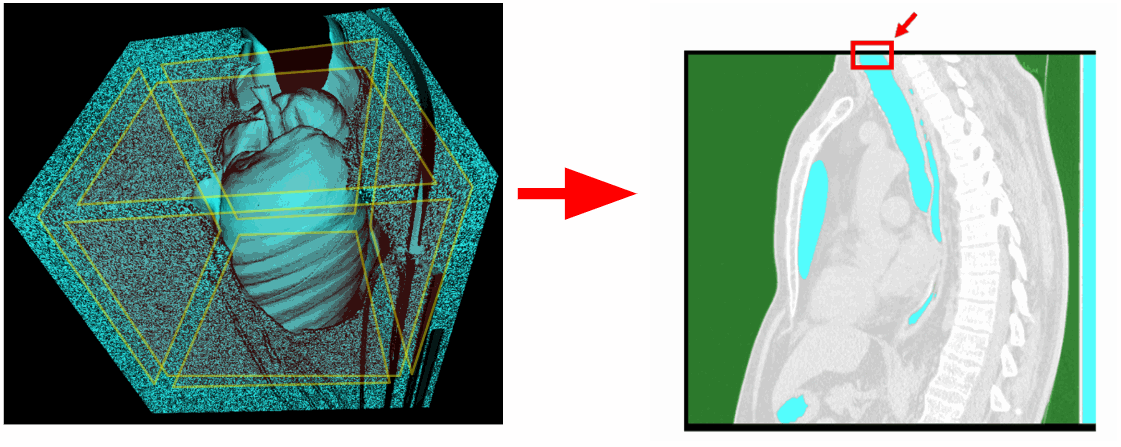
Es necesario excluir el plano superior de la zona de escaneo. También hay estudios en los que los pulmones no se capturaron por completo y el plano inferior está asociado con los pulmones. Entonces, si se desea, el plano inferior también puede ser excluido.

Pero este método solo actúa en estudios de mama. En el caso de capturar el volumen completo del cuerpo, aparecerá una conexión entre el aire interno y externo a través de la cavidad nasal en la imagen. Por lo tanto, es necesario aplicar erosión morfológica para separar el aire interno y externo.
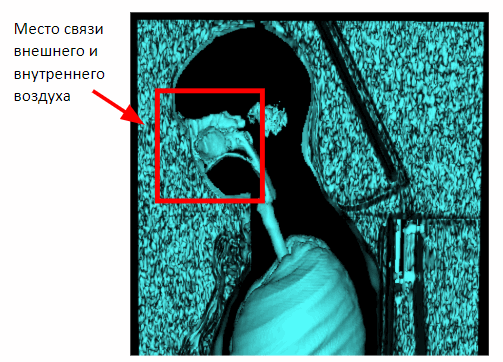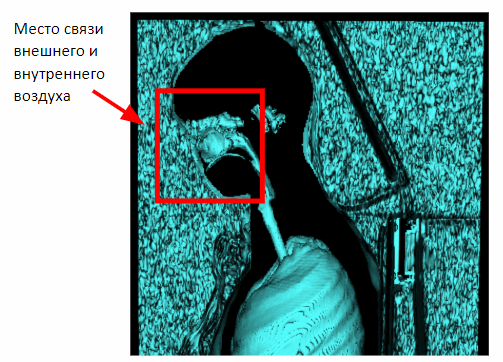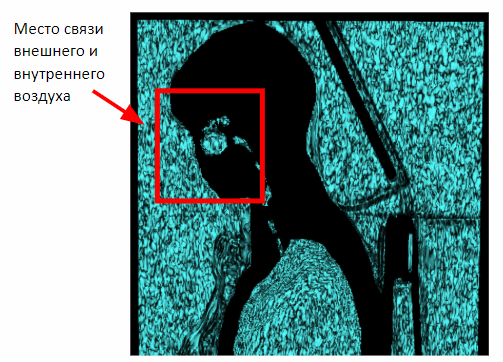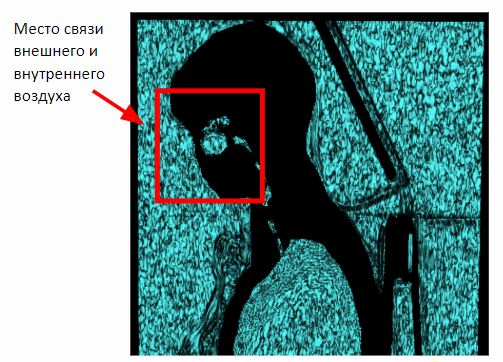
Después de aplicar la erosión, podemos volver al método previamente obtenido de segmentación del aire externo basado en la proximidad a los planos laterales de la escena.

Al aislar el aire externo, uno puede sacarlo inmediatamente del volumen total de aire y pulmones y obtener el aire interno del cuerpo y los pulmones. Pero hay un problema. Después de la erosión, se perdió parte de la información sobre el aire exterior. Para restaurarlo, aplicamos la dilatación del aire externo.

Luego, restamos el aire externo de todos los órganos respiratorios y de aire y obtenemos el aire interno y los órganos respiratorios.


Destacando el objeto máximo en volumen
A continuación, seleccionamos los órganos respiratorios como el objeto más grande en volumen. Los órganos respiratorios son un objeto separado. No hay conexión entre los pulmones y el aire dentro del tracto gastrointestinal.


Vale la pena señalar que la elección correcta del umbral de densidad de rayos X en el paso inicial de la transformación del umbral es importante. De lo contrario, en algunos casos, puede no haber una conexión entre los dos pulmones como resultado de la baja resolución. Por ejemplo, si considera que los vóxeles de los órganos respiratorios tienen una densidad de rayos X de -500 HU o menos, entonces, en el caso a continuación, la asignación de los órganos respiratorios como el objeto más grande en volumen conducirá a un error, ya que no hay conexión entre los dos pulmones. Por lo tanto, el umbral debe aumentarse a -300 HU.

Cierre vascular dentro de los pulmones.
Para capturar los vasos dentro de los pulmones, usamos cierre morfológico, es decir, dilatación seguida de erosión con el mismo radio. La densidad de rayos X de los vasos es de aproximadamente -100..100 HU.

Los vasos sanguíneos grandes no se cerraron. Pero esto no es necesario. El propósito de esta operación era destruir muchos agujeros pequeños dentro de los pulmones para facilitar una mayor segmentación pulmonar.
Algoritmo de segmentación respiratoria
Como resultado, obtenemos el siguiente algoritmo de segmentación de órganos respiratorios:
- Umbral de conversión de volumen base por umbral <-300 HU.
- Erosión morfológica con un radio de 3 mm para la separación del aire externo e interno.
- La asignación de aire externo sobre la base de la proximidad a los planos laterales limítrofes de la escena del vóxel.
- Dilatación morfológica del aire externo para restaurar la información perdida como resultado de la erosión.
- Resta de aire externo de todos los órganos respiratorios y de aire para obtener aire interno y órganos respiratorios.
- Destacando el objeto máximo en volumen.
- Cierre morfológico de los vasos sanguíneos dentro de los pulmones.

Implementación del algoritmo en MATLAB
Método GetRespiratoryOrgans
Método GetExternalAir
Método GetMaxObject
El código fuente se puede descargar aquí .
Conclusión
Se planean los siguientes artículos:
- segmentación de la tráquea y los bronquios;
- segmentación de los pulmones;
- segmentación de los lóbulos de los pulmones.
Algoritmos como:
- transformación de distancia;
- transformación vecina más cercana (transformación vecina más cercana, también conocida como transformación de características);
- cálculo de valores propios de la matriz de Hesse para la segmentación de objetos planos en 3D;
- segmentación por la segmentación de la cuenca.