Alexey Savvateev: Modelos de Internet y redes sociales.

"La única razón de la existencia de la economía es inspirar a los matemáticos a nuevas hazañas".



En 2013, Alexey Savvateev dio varias conferencias sobre modelos de redes sociales e Internet. Encontré este tema muy curioso y olvidado inmerecidamente. Tratemos de entender el problema. También me interesa saber cómo ha cambiado la situación desde entonces y qué publicaciones útiles hay en esta área.

Tanto en Internet como en la biología de las redes sociales, exhiben propiedades que los modelos describen individualmente, pero en conjunto confunden las matemáticas modernas. Savvateev afirma que "quien se encargue de esto recibirá el Premio Nobel". El futuro dependerá de la capacidad de trabajar con redes.

Lo siguiente es un resumen compilado de tres videos de conferencias, el video en sí está al final. (La publicación parece un conjunto de diapositivas con citas de conferenciantes, para unir todo en un texto único y elegante, me faltan las habilidades para el idioma ruso y las matemáticas, pero el tema es muy importante, por lo que quiero publicarlo).

La red social consiste en:

• Agentes
• Comunicaciones entre agentes.

Las conexiones pueden ser bidireccionales (amigos, coautoría) y pueden ser unidireccionales (suscriptores). Las redes sociales siempre existieron, pero estudiarlas a nivel macro solo fue posible con el advenimiento de las redes en línea. La humanidad en los últimos 10 años ha dado un salto cuántico. Aprendió a examinarse a sí mismo como un todo. Se puede digitalizar. Recopila información sobre ti.

Sería justo construir un modelo de gráficos ponderados cuando se indican los coeficientes de la "fuerza de enlace". Pero para nosotros como antes a la luna.

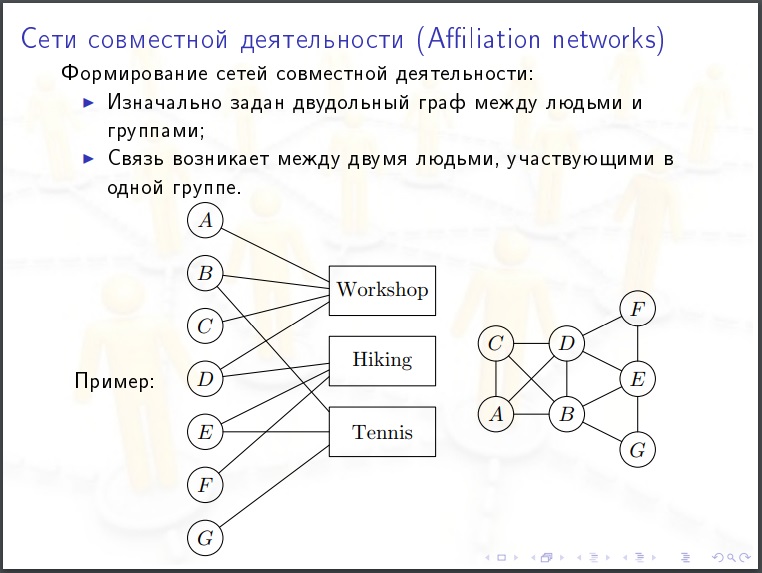
Galeria

Es útil mirar las fotos. La hipótesis que podría presentar después de ver la imagen puede ser obviamente absurda.

¿Quién es útil para estudiar las redes sociales?

Economía: se supone que los niveles micro y macro en la economía están conectados a través de una "red"
Ciencia política: se asume si el régimen se mantendrá o cambiará, dependiendo de quién tendrá especialistas en redes más poderosos.



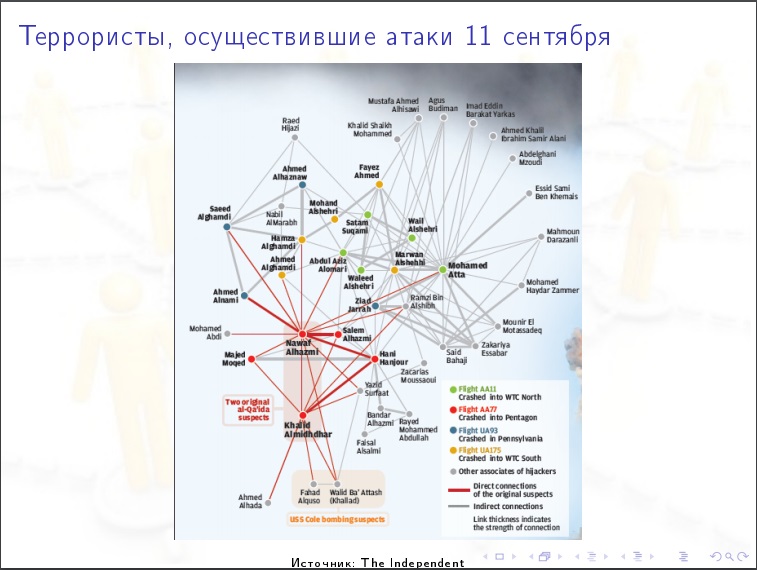Ejemplo de análisis de redes sociales.

Características numéricas de las redes sociales.

• Distancia
• Diámetro
• Grado de vértice
• Distribución de grados de vértice
• Medidas de centralidad de nodo
• Distribución de centralidad
• Coeficiente de agrupamiento
• Coeficiente de surtido

Distancia : cuántos bordes necesita pasar para pasar de un vértice a otro.

El diámetro es la distancia máxima en el gráfico.

El grado de un vértice es el número de aristas en el vértice.

Teoría de los seis apretones de manos

Cualquier gráfico social tiene un diámetro promedio muy bajo ( Teoría de los seis apretones de manos ). Además, hay un núcleo muy denso. Estoy "familiarizado" con algunos africanos, a través de mi presidente, que le dio la mano al presidente africano.







Coeficiente de agrupamiento local . Nos fijamos en todos los vecinos de una persona, "k" piezas. Costillas máximas - k (k-1) / 2. Observamos el número real de aristas y dividimos por este máximo.

Factor de agrupamiento global . Cuántos "triángulos" en comparación con "marcas de verificación".





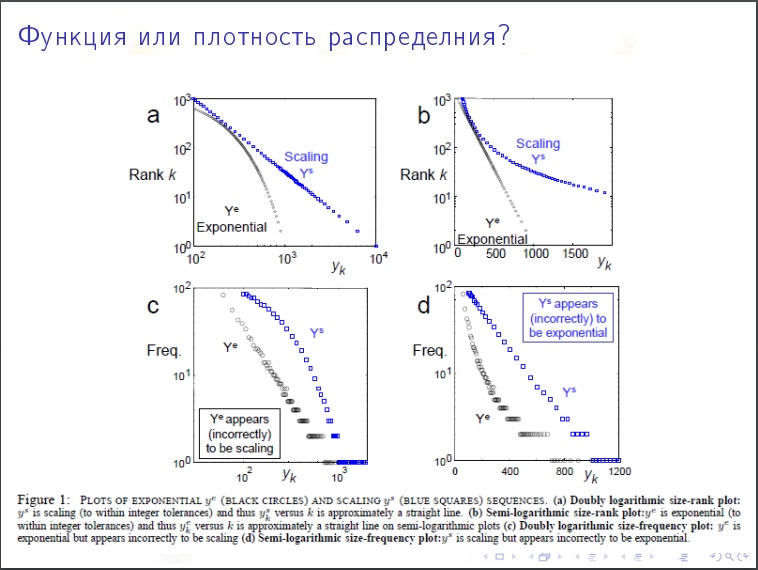
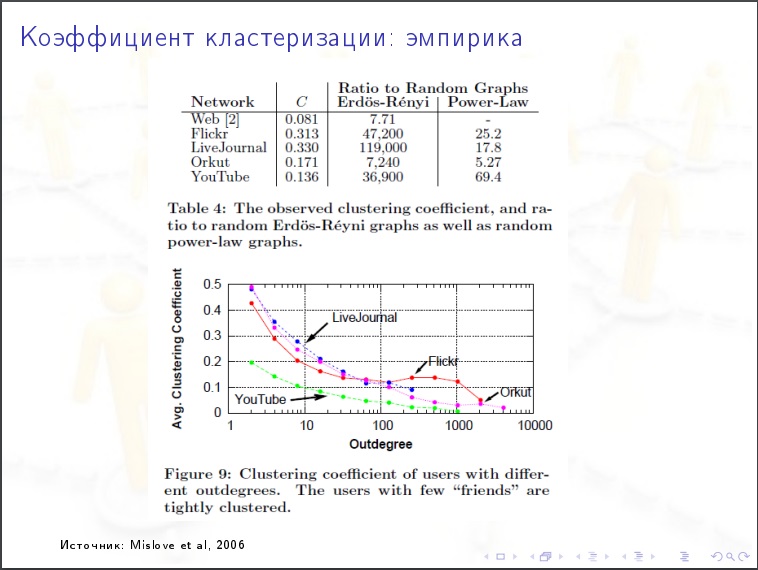La distribución en grados del vértice . ¿Qué porcentaje de vértices tiene grados inferiores a 1000? ¿La naturaleza de la distribución es exponencial o exponencial? Resulta que Internet tiene una naturaleza tranquila.

El coeficiente es "2". Los vértices cuyo grado es "x" serán N / x ² . Verificamos que en LJ mil millones de usuarios, las milésimas deben dividirse entre mil y mil cuadrados. Mil milésimas.

Esto es una cosa que disminuye muy lentamente.













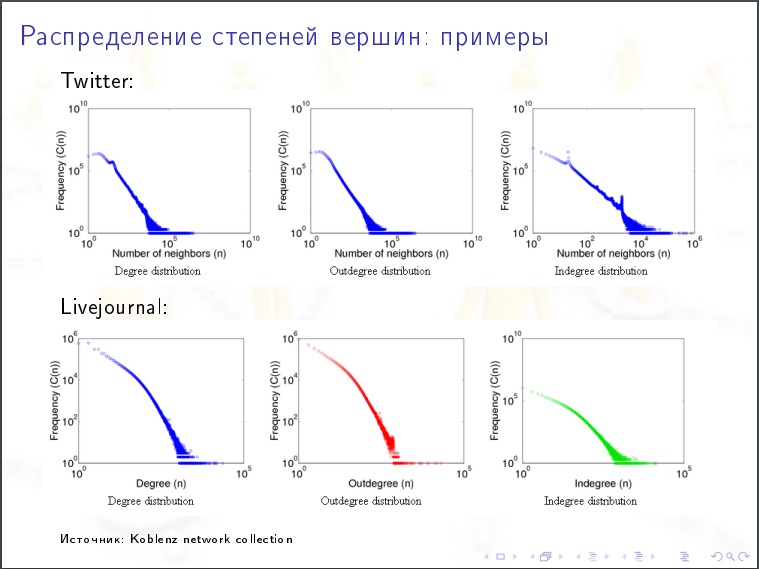
Coeficiente de surtido . enfoque aproximado: tomamos picos con aproximadamente el mismo número de grados, ¿es más probable que estén conectados entre sí o con menos? Si es así, entonces se clasifica. Disortatividad: cuando con una gran cantidad de grados es más probable que se asocie con menos. Este es un enfoque ingenuo. Un enfoque más correcto es este. En cada vértice hay alguna otra característica (capital total del banco), y se ve la variedad por este indicador.





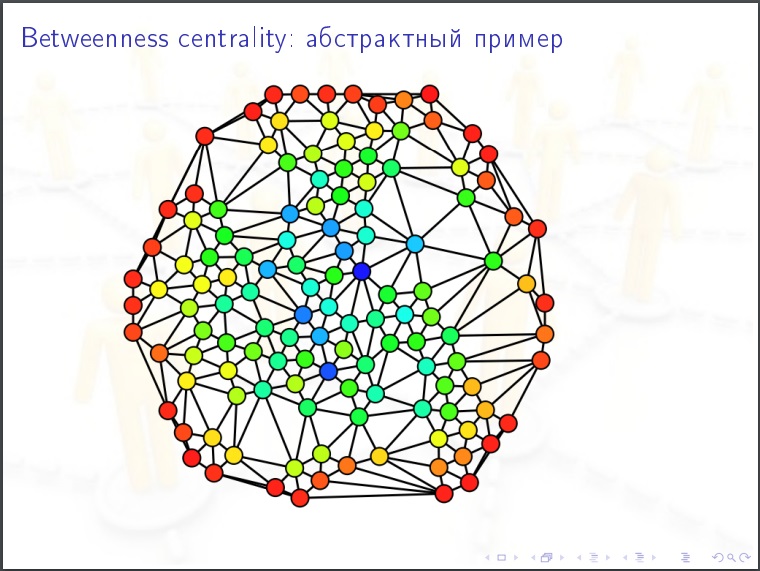
La centralidad del nodo para una red social. Tomamos una persona, consideramos el siguiente valor para ella. Ordenamos todos los pares de otras personas (N-1) (N-2) / 2 y en cada caso preguntamos, la ruta de citas más cercana en el gráfico, ¿pasa por esta persona? Puede haber varios caminos más cortos y algunos de ellos contienen a nuestra persona, luego le damos%. Esta es la característica más importante en las redes sociales. Por la propagación de epidemias, opinión pública. Esto es lo que debe medirse.









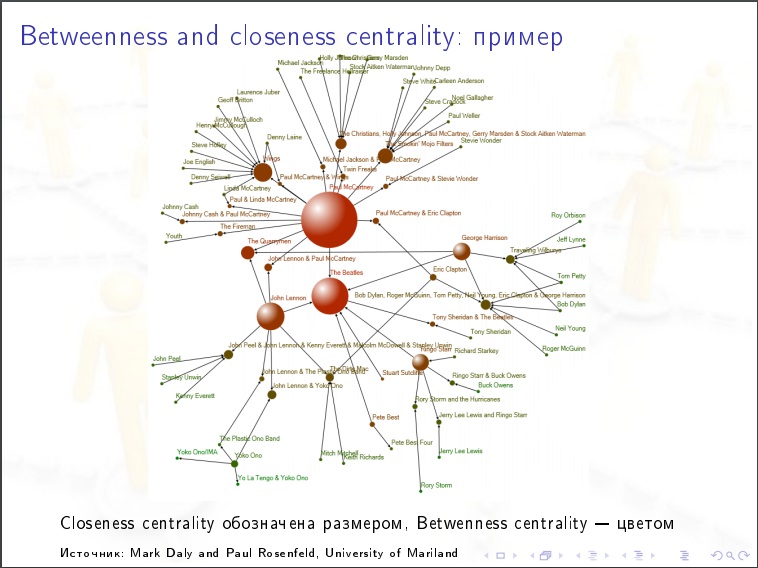
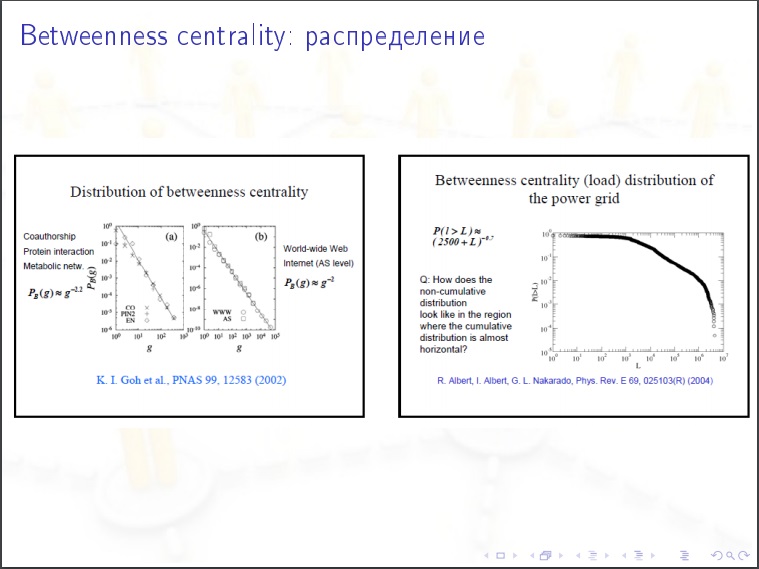
Características de las redes sociales:

• Diámetro pequeño y distancia media entre vértices.
• La ley de poder de la distribución de grados de vértices y centralidad de intermediación
• Alta relación de agrupamiento
• Surtido
• La presencia de un núcleo estrechamente relacionado

La tarea es crear un modelo que cubra las tres primeras propiedades (y preferiblemente las dos últimas). Los tres primeros ya son una complejidad insuperable en este momento. Para 2013, no existe tal modelo.

Pasamos a la descripción de modelos de gráficos aleatorios que existían.

Modelos

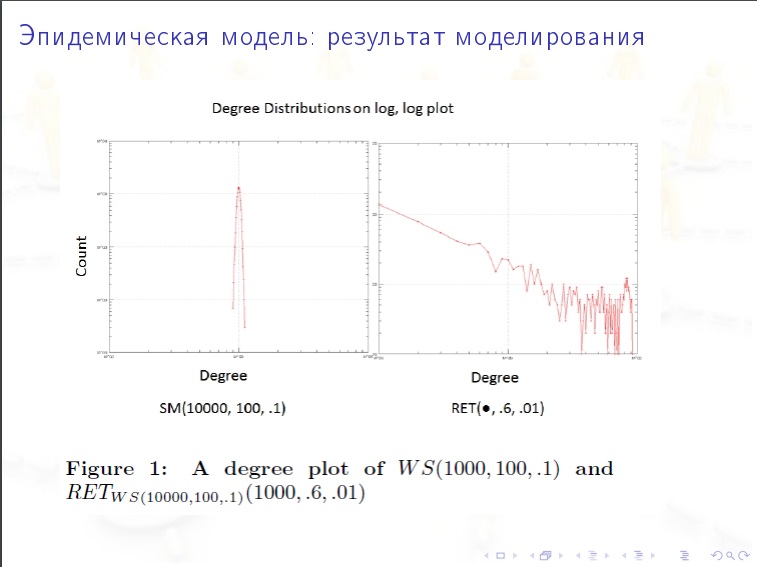
Los modelos son:

• Técnico (los bordes se generan aleatoriamente)
• Juego teórico (cuando es beneficioso para alguien)
• Sin estructura (solo muchos vértices)
• Estructural (los vértices son puntos de espacio métrico o tienen pesos; hay una estructura en el conjunto de vértices)

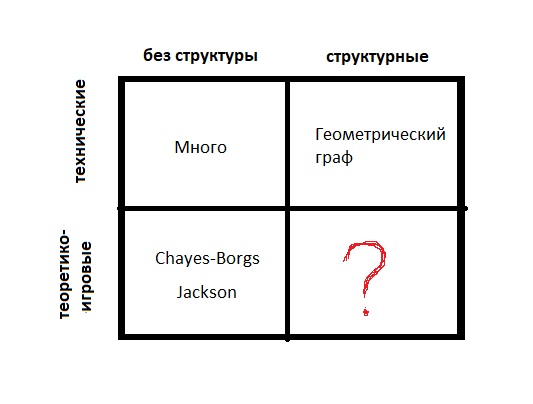
Si comprende lo que subyace, puede guiarse por una gran cantidad de parámetros. Si los parámetros bien elegidos dan una buena aproximación, entonces está bien hecho. E incluso si la mejor combinación da un mal resultado y no es consistente con los hechos observados, entonces adiós.

Todo esto se hace con un propósito: combatir el correo no deseado.

Internet se puede imaginar como una red compleja en varios niveles:

• Nivel tecnologico . Los vértices y los bordes son nodos y líneas de comunicación.
• Nivel de hipertexto . Los vértices son sitios o páginas, y los bordes son hipervínculos.
• Nivel social Los vértices son usuarios, y los bordes son esas u otras conexiones entre ellos: amistades en redes sociales, suscripción a blogs, colaboración en proyectos distribuidos (por ejemplo, wikipedia), etc.

Para redes complejas, se conocen muchas características numéricas locales y globales: la distribución de grados de vértices, el coeficiente de agrupamiento, el coeficiente de surtividad

Resulta que una serie de características son características de las redes de Internet:

• Paretto distribucion de grados
• alto coeficiente de agrupamiento,
• surtividad positiva
• diámetro pequeño

El objetivo final de modelar redes de Internet es construir modelos con las mismas características.

Modelo Erdos - Renyi

El modelo Erdos - Renyi es uno de los dos modelos de generación de gráficos aleatorios estrechamente relacionados. Los modelos llevan el nombre de los matemáticos Pal Erdös y Alfred Renyi, quienes fueron los primeros en presentar uno de los modelos en 1959. Explorado el gráfico de citas.

Considere N puntos. Bordes potenciales - N * (N-1) / 2. Para cada costilla realizamos una prueba aleatoria. La probabilidad de que ocurriera la costilla - p. Lo que no sucedió - (1-p). Ejecutemos la "prueba", obtenemos un gráfico. Pero hay algunos problemas. Para que aparezca la propiedad de "dispersión", p debe ser muy pequeña, del orden de 1 / N, y luego el diámetro será muy grande.

Cualquier investigador que escuche que Internet se describe como un gráfico aleatorio según el modelo Erds-Renyi se reirá.

Un efecto interesante es que cuando superas un cierto umbral de probabilidad, el gráfico se conecta.

Modelo Bollobashi

Este es un modelo dinámico para construir Internet. Estamos tratando de adivinar cómo se formó gradualmente. La idea es esta. Tomamos una gráfica con un vértice y un borde, y luego en cada paso jugamos al azar. Agregamos un vértice, después de eso, con cierta probabilidad, se cierra sobre sí mismo, y con cierta probabilidad se conecta al anterior. El siguiente pico con cierta probabilidad se cierra sobre sí mismo, y con algunos va a uno de los anteriores. Además, la probabilidad de golpear la parte superior siempre es proporcional al número de aristas que hay. Se juega un valor aleatorio y el siguiente sorteo depende del resultado del anterior. Tal modelo es intuitivo, pero matemáticamente difícil de calcular. Este modelo proporciona una distribución de potencia no exponencial. El diámetro es el mismo.

Pero este modelo no funciona con la agrupación.

Hay dos enfoques competitivos que funcionan con la agrupación.

Enfoque geométrico

La suposición se toma desde el techo. El gráfico de Internet se basa en el espacio métrico. El espacio de gustos, intereses, preferencias. Qué interesantes son las personas entre sí. Qué cerca en espíritu, en opinión. Si las personas son cercanas, se refieren entre sí.

Tomamos y arrojamos 10 ¹⁰ puntos en este espacio. Una gran cantidad de parámetros aparecen aquí. Enorme

La agrupación es excelente, pero los vértices decrecientes son exponenciales. Controversia

Este método es terriblemente simple y los algoritmos se realizan "por casualidad".

Enfoque teórico del juego Game-Borgs

¿Sabías que en los días de von Neumann se anunció que la teoría de juegos sería un arma de nueva generación contra la Unión Soviética?

Asumimos que las personas toman decisiones para comunicarse entre sí o no.

Organizamos reuniones / eventos. Un evento es una lista de invitados, así como su "intensidad".
Costos = Intensidad * (constante + K * (número de invitados)). Tengo que gastar recursos para "vender" el evento y tengo que gastar más en cada participante. Hay cumpleaños y hay caminatas. Aparece el coeficiente "P", que es pequeño para un cumpleaños y grande para una caminata. Intensidad de citas.

Una persona puede organizar varios eventos con intensidades P ₁ , P ₂ ... P _n . Otros hacen lo mismo.

Existen mis acciones para establecer lazos sociales, y hay extraños.

Función ganadora = (el número de personas con las que te has familiarizado bastante) - costos

"Lo suficientemente familiar" significa que la suma de las intensidades de todos los eventos en los que estuvieron juntos es mayor que un cierto valor umbral. Y no importa quién organizó el evento.

Las costillas se llevan a cabo para conocidos suficientemente buenos.



Está comprobado que en este modelo se obtienen muchas propiedades de cierre real. En todos los equilibrios de Nash, también se observan propiedades de cierre reales e incluso propiedades de agrupación más fuertes, que también se observan en el gráfico de Internet real.



Pero no hay nada claro sobre las otras propiedades, pero esto es la mitad del problema. El problema es que si hay al menos un equilibrio de Nash donde al menos dos personas se conocen, entonces hay un equilibrio de Nash en el que todos están familiarizados con todos.





Hay una idea para combinar los dos enfoques. Para considerar que las personas viven en un espacio métrico, y cuando organizan eventos, o participan en un evento, las relaciones de costo, intensidad y umbral dependen de la "proximidad". Esta es la quinta generación de modelos.

Costos diferenciados

Las opciones son hacer costos diferenciados y ganancias diferenciadas. Algunos son más fáciles de invitar que otros. Conocer a uno es más rentable que conocer a otro.





Supongamos que organizamos a todas las personas de manera uniforme alrededor de la circunferencia. Y es más barato invitar a alguien más cercano. ¿Cómo será el equilibrio? Todos invitarán a algún barrio, ¿verdad? No es verdad No existe tal equilibrio.

Prueba. Supongamos que existe, entonces las personas cercanas ya están invitadas a muchas reuniones diferentes. Entonces no necesita invitar a este ser querido. La existencia de este equilibrio contradice la existencia de este equilibrio.



El equilibrio puro existe, se encuentra, es el único. Cada uno invita a un vecindario que se encuentra (o en sentido contrario a las agujas del reloj) a una cierta distancia y una cierta longitud.

(- ¡Esta es la formación de galaxias!)
(- ¡Esta es una ruptura espontánea de simetría!)

Conclusiones

Pelevin escribió una vez que "el significado de la vida rusa está en el dorado sin prisas de un inmenso iconostasio". Este es el significado de las matemáticas, en el mismo. Solo el iconostasio es científico.



Este es un estudio altamente multidisciplinario. Más alto como te puedas imaginar.

Fuentes

PS

“Una vez que fui llamado al club a Navalny, hay algunos jóvenes, entusiastas que lo ayudan. Inmediatamente advertí que diría cosas desagradables. Una revolución es victoriosa si los matemáticos que están a favor de la revolución son más fuertes que los que están en contra. Los jóvenes de Navalny no sabían cómo contarles tales modelos, pero no entienden, ni siquiera saben cómo integrarse, simplemente corren y gritan en alguna parte. Y contra ellos se encuentra una institución fuerte con personas serias a la cabeza, quienes, por orden del Kremlin, dicen exactamente quién y cuánto deben arrestar para que no haya nada. Dicen: "Estamos descentralizados, específicamente Navalny no significa nada, hay varios líderes importantes". Y luego viene un matemático y cree que la centralización es el 90% de esta red. Bloqueas a alguien que necesitas por unos días, y no hay revolución. Matemáticas gana ".
- Alexey Savvateev, "La revolución gana si tiene buenos matemáticos"

PPS

Quién sabe qué otras obras interesantes (artículos, conferencias) hay obras en el campo de las redes sociales y sus beneficios prácticos, por favor comparta.