Redes neuronales y aprendizaje profundo, capítulo 3, parte 1: mejorar la forma en que se entrenan las redes neuronales

Cuando una persona aprende a jugar al golf, generalmente pasa la mayor parte de su tiempo preparando un golpe básico. Luego se acerca a otros golpes, gradualmente, estudiando estos o esos trucos, basándose en el golpe básico y desarrollándolo. Del mismo modo, hasta ahora nos hemos centrado en comprender el algoritmo de retropropagación. Este es nuestro "golpe básico", la base para la capacitación de la mayoría del trabajo con redes neuronales (NS). En este capítulo, hablaré sobre un conjunto de técnicas que se pueden utilizar para mejorar nuestra implementación más simple de la propagación hacia atrás y para mejorar la forma de enseñar NS.

Entre las técnicas que aprenderemos en este capítulo están: la mejor opción para el papel de la función de costo, a saber, la función de costo con entropía cruzada; cuatro llamados métodos de regularización (regularización de L1 y L2, exclusión de neuronas [abandono], extensión artificial de datos de entrenamiento), que mejoran la generalización de nuestro NS más allá de los límites de los datos de entrenamiento; mejor método para inicializar pesos de red; Un conjunto de métodos heurísticos para ayudarlo a elegir buenos hiperparámetros para la red. También consideraré varias otras técnicas, un poco más superficialmente. En su mayor parte, estas discusiones son independientes entre sí, por lo que puede saltar sobre ellas si lo desea. También implementamos muchas tecnologías en el código de trabajo y las usamos para mejorar los resultados obtenidos para la tarea de clasificar números escritos a mano, que se estudió en el Capítulo 1.

Por supuesto, consideramos solo una fracción de la gran cantidad de técnicas desarrolladas para su uso con redes neuronales. La conclusión es que la mejor manera de ingresar al mundo de la abundancia de técnicas disponibles es estudiar en detalle algunas de las más importantes. El dominio de estas técnicas importantes no solo es útil en sí mismo, sino que también profundizará su comprensión de los problemas que pueden surgir al usar redes neuronales. Como resultado, estará preparado para adaptar rápidamente nuevas técnicas según sea necesario.

Función de costo de entropía cruzada

La mayoría de nosotros odiamos estar equivocados. Poco después de comenzar a aprender el piano, ofrecí un pequeño concierto frente a una audiencia. Estaba nervioso y comencé a tocar una pieza una octava más baja de lo necesario. Estaba confundido y no podía continuar hasta que alguien me señalara un error. Estaba muy avergonzado Sin embargo, aunque esto es desagradable, también aprendemos muy rápidamente, decidiendo que estábamos equivocados. ¡Y ciertamente la próxima vez que hablé con la audiencia, toqué en la octava correcta! Por el contrario, aprendemos más lentamente cuando nuestros errores no están bien definidos.

Idealmente, esperamos que nuestras redes neuronales aprendan rápidamente de sus errores. ¿Esto sucede en la práctica? Para responder a esta pregunta, veamos un ejemplo descabellado. Implica una neurona con solo una entrada:



Estamos enseñando a esta neurona a hacer algo ridículamente simple: aceptar 1 y dar 0. Por supuesto, podríamos encontrar una solución a un problema tan trivial seleccionando manualmente el peso y la compensación, sin usar el algoritmo de entrenamiento. Sin embargo, será bastante útil intentar usar el descenso en gradiente para obtener peso y desplazamiento como resultado del entrenamiento. Veamos cómo se entrena una neurona.

Para mayor claridad, elegiré un peso inicial de 0.6 y un desplazamiento inicial de 0.9. Estos son algunos valores generales asignados como punto de partida, y no los seleccioné específicamente. Inicialmente, una neurona de salida produce 0,82, por lo que debemos aprender mucho para acercarnos a la salida deseada de 0,0. El artículo original tiene un formulario interactivo en el que puede hacer clic en "Ejecutar" y observar el proceso de aprendizaje. Esta animación no está pregrabada, el navegador realmente calcula el gradiente y luego lo usa para actualizar el peso y el desplazamiento, y muestra el resultado. La velocidad de aprendizaje es η = 0.15, lo suficientemente lenta como para poder ver lo que está sucediendo, pero lo suficientemente rápida como para que el aprendizaje tenga lugar en segundos. La función de costo C es cuadrática, presentada en el primer capítulo. Pronto te recordaré su forma exacta, por lo que no es necesario volver y hurgar allí. El entrenamiento se puede iniciar varias veces simplemente haciendo clic en el botón "Ejecutar".

Como puede ver, la neurona aprende rápidamente el peso y el sesgo, lo que reduce el costo, y da una producción de 0.09. Este no es el resultado deseado de 0.0, pero es bastante bueno. Supongamos que elegimos un peso inicial y un desplazamiento de 2.0 en su lugar. En este caso, la salida inicial será 0.98, lo cual es completamente incorrecto. Veamos cómo en este caso la neurona aprenderá a producir 0.

Aunque este ejemplo usa la misma tasa de aprendizaje (η = 0.15), vemos que el aprendizaje es más lento. Alrededor de 150 de las primeras épocas, pesos y desplazamientos apenas cambian. Luego, el entrenamiento se acelera y, casi como en el primer ejemplo, la neurona se mueve rápidamente a 0.0. Este comportamiento es extraño, no como aprender una persona. Como dije al principio, a menudo aprendemos más rápido cuando estamos muy equivocados. Pero acabamos de ver cómo nuestra neurona artificial aprende con gran dificultad, cometiendo muchos errores, mucho más difícil que cuando cometió un pequeño error. Además, resulta que tal comportamiento surge no solo en nuestro ejemplo simple, sino también en un NS de propósito más general. ¿Por qué el aprendizaje es tan lento? ¿Puedo encontrar una manera de evitar este problema?

Para comprender la fuente del problema, recordamos que nuestra neurona aprende a través de cambios en el peso y el desplazamiento a una velocidad determinada por las derivadas parciales de la función de costo, ∂C / ∂w y ∂C / ∂b. Entonces decir "aprender es lento" es lo mismo que decir que estas derivadas parciales son pequeñas. El problema es entender por qué son pequeños. Para hacer esto, calculemos las derivadas parciales. Recuerde que usamos la función de costo cuadrático, que viene dada por la ecuación (6):

$$

$$C = \ frac {(y-a) ^ 2} {2} \ tag {54}$$

donde a es la salida de la neurona cuando x = 1 se usa en la entrada, y y = 0 es la salida deseada. Para escribir esto directamente a través del peso y el desplazamiento, recuerde que a = σ (z), donde z = wx + b. Usando la regla de la cadena para la diferenciación por peso y desplazamiento, obtenemos:

$$

$$\ frac {\ partial C} {\ partial w} = (a-y) \ sigma '(z) x = a \ sigma' (z) \ tag {55}$$

$$

$$\ frac {\ partial C} {\ partial b} = (a-y) \ sigma '(z) = a \ sigma' (z) \ tag {56}$$

donde sustituí x = 1 e y = 0. Para comprender el comportamiento de estas expresiones, echemos un vistazo más de cerca al término σ '(z) a la derecha. Recordemos la forma de un sigmoide:



El gráfico muestra que cuando la salida de la neurona es cercana a 1, la curva se vuelve muy plana y σ '(z) se vuelve pequeña. Las ecuaciones (55) y (56) nos dicen que ∂C / ∂w y ∂C / ∂b se vuelven muy pequeñas. De ahí la desaceleración en el aprendizaje. Además, como veremos un poco más tarde, la desaceleración de la capacitación ocurre, de hecho, por la misma razón y en la Asamblea Nacional de una forma más general, y no solo en nuestro ejemplo más simple.

Introducción de la función de costo de entropía cruzada

¿Qué hacemos con ralentizar el aprendizaje? Resulta que podemos resolver el problema reemplazando la función cuadrática de valor con otra función de valor, conocida como entropía cruzada. Para entender la entropía cruzada, nos alejamos de nuestro modelo más simple. Supongamos que entrenamos una neurona con varios valores de entrada x ₁ , x ₂ , ... pesos correspondientes w ₁ , w ₂ , ... y desplazamiento b:



La salida de la neurona, por supuesto, será a = σ (z), donde z = ∑ _j w _j x _j + b es la suma ponderada de las entradas. Definimos la función de costo de entropía cruzada para una neurona dada como

$$

$$C = - \ frac {1} {n} \ sum_x \ left [y \ ln a + (1-y) \ ln (1-a) \ right] \ tag {57}$$

donde n es el número total de unidades de datos de entrenamiento, la suma va sobre todos los datos de entrenamiento x, e y es la salida deseada correspondiente.

No es obvio que la ecuación (57) resuelva el problema de ralentizar el aprendizaje. Honestamente, ¡ni siquiera es obvio que tenga sentido llamarlo una función de valor! Antes de pasar a la desaceleración en el aprendizaje, veamos en qué sentido la entropía cruzada puede interpretarse como una función de valor.

Dos propiedades en particular hacen que sea razonable interpretar la entropía cruzada como una función de valor. En primer lugar, es mayor que cero, es decir, C> 0. Para ver esto, tenga en cuenta que (a) todos los miembros individuales de la suma en (57) son negativos, ya que ambos logaritmos se toman de números en el rango de 0 a 1, y (b) el signo menos está delante de la suma.

En segundo lugar, si la salida real de la neurona está cerca de la salida deseada para todas las entradas de entrenamiento x, entonces la entropía cruzada estará cerca de cero. Para probar esto, tendremos que suponer que las salidas deseadas y serán 0 o 1. Por lo general, esto sucede al resolver problemas de clasificación o al calcular funciones booleanas. Para comprender qué sucede si no hace tal suposición, consulte los ejercicios al final de la sección.

Para probar esto, imagine que y = 0 y a≈0 para alguna entrada x. Así será cuando la neurona maneje bien esa entrada. Vemos que el primer término de expresión (57) para el valor desaparece, ya que y = 0, y el segundo será −ln (1 - a) ≈0. Lo mismo es cierto cuando y = 1 y a≈1. Por lo tanto, la contribución del valor será pequeña si la salida real es cercana a la deseada.

En resumen, obtenemos que la entropía cruzada es positiva y tiende a cero cuando la neurona calcula mejor la salida deseada y para todas las entradas de entrenamiento x. Esperamos la presencia de ambas propiedades en la función de costo. Y, de hecho, ambas propiedades se cumplen mediante el valor cuadrático. Por lo tanto, para la entropía cruzada es una buena noticia. Sin embargo, la función de costo de entropía cruzada tiene una ventaja porque, a diferencia del valor cuadrático, evita el problema de ralentizar el aprendizaje. Para ver esto, calculemos la derivada parcial del valor con entropía cruzada en peso. Sustituya a = σ (z) en (57), aplique la regla de la cadena dos veces y obtenga

$$

$$\ frac {\ partial C} {\ partial w_j} = - \ frac {1} {n} \ sum_x \ left (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ right) \ frac {\ partial \ sigma} {\ partial w_j} \ tag {58}$$

$$

$$= - \ frac {1} {n} \ sum_x \ left (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ right) \ sigma '(z) x_j \ tag {59}$$

Reduciendo a un denominador común y simplificando, obtenemos:

$$

$$\ frac {\ partial C} {\ partial w_j} = \ frac {1} {n} \ sum_x \ frac {\ sigma '(z) x_j} {\ sigma (z) (1- \ sigma (z)) } (\ sigma (z) -y). \ tag {60}$$

Usando la definición de sigmoide, σ (z) = 1 / (1 + e ^−z ) y un poco de álgebra, podemos mostrar que σ ′ (z) = σ (z) (1 - σ (z)). Le pediré que verifique esto más adelante en el ejercicio, pero por ahora, acéptelo como la verdad. Los términos σ (z) y σ (z) (1 - σ (z)) se cancelan, y esto lleva a

$$

$$\ frac {\ partial C} {\ partial w_j} = \ frac {1} {n} \ sum_x x_j (\ sigma (z) -y). \ tag {61}$$

Gran expresion. De esto se deduce que la velocidad con la que se entrenan las pesas está controlada por σ (z) −y, es decir, por un error en la salida. Cuanto mayor es el error, más rápido aprende la neurona. Esto podría esperarse intuitivamente. Esta opción evita la desaceleración en el aprendizaje causada por el término σ '(z) en una ecuación de costo cuadrático similar (55). Cuando usamos entropía cruzada, el término σ '(z) se reduce y ya no tenemos que preocuparnos por su pequeñez. Esta reducción es un milagro especial garantizado por la función de costo de entropía cruzada. De hecho, por supuesto, esto no es un verdadero milagro. Como veremos más adelante, la entropía cruzada se eligió específicamente para esta propiedad.

Del mismo modo, se puede calcular la derivada parcial para el sesgo. No volveré a dar todos los detalles, pero puedes comprobarlo fácilmente

$$

$$\ frac {\ partial C} {\ partial b} = \ frac {1} {n} \ sum_x (\ sigma (z) -y). \ tag {62}$$

Esto nuevamente ayuda a evitar el retraso del aprendizaje debido al término σ '(z) en una ecuación similar para el valor cuadrático (56).

Ejercicio

• Verifique que σ ′ (z) = σ (z) (1 - σ (z)).

Volvamos a nuestro ejemplo descabellado con el que jugamos anteriormente y veamos qué sucede si usamos entropía cruzada en lugar del valor cuadrático. Para sintonizar, comenzamos con el caso en el que el costo cuadrático funcionó perfectamente cuando el peso inicial era 0.6 y el desplazamiento era 0.9. El artículo original tiene una forma interactiva en la que puede hacer clic en el botón Ejecutar y ver qué sucede cuando reemplaza el valor cuadrático con entropía cruzada.

No es sorprendente que la neurona en este caso esté perfectamente entrenada, como antes. Ahora echemos un vistazo al caso en el que la neurona se quedaba atascada , con un peso y desplazamiento a partir de 2.0.



Éxito! Esta vez la neurona aprendió rápidamente, como queríamos. Si observa detenidamente, puede ver que la pendiente de la curva de costos es inicialmente más pronunciada en comparación con la región plana de la curva de valor cuadrático correspondiente. Esta entropía a campo traviesa nos da esta frialdad, y no nos deja atascarnos donde esperamos el entrenamiento más rápido de una neurona cuando comienza con grandes errores.

No dije qué velocidad de entrenamiento se utilizó en los últimos ejemplos. Anteriormente, con un valor cuadrático, utilizamos η = 0.15. ¿Deberíamos usar la misma velocidad en los nuevos ejemplos? De hecho, al cambiar la función de costo, es imposible decir exactamente qué significa usar la "misma" velocidad de aprendizaje; Será una comparación de manzanas con naranjas. Para ambas funciones de costo, experimenté buscando una velocidad de aprendizaje que me permitiera ver lo que está sucediendo. Si todavía está interesado, en los últimos ejemplos, η = 0.005.

Puede argumentar que cambiar la velocidad de aprendizaje hace que los gráficos no tengan sentido. ¿A quién le importa qué tan rápido aprende una neurona si podemos elegir arbitrariamente una velocidad de aprendizaje? Pero esta objeción no tiene en cuenta el punto principal. El significado de los gráficos no está en la velocidad absoluta de aprendizaje, sino en cómo cambia esta velocidad. Cuando se utiliza la función cuadrática, el entrenamiento es más lento si la neurona está muy equivocada, y luego se acelera cuando la neurona se acerca a la respuesta deseada. Con la entropía cruzada, el aprendizaje es más rápido cuando una neurona comete un gran error. Y estas declaraciones no dependen de una velocidad de aprendizaje dada.

Examinamos la entropía cruzada para una neurona. Sin embargo, esto es fácil de generalizar a redes con muchas capas y muchas neuronas. Suponga que y = y ₁ , y ₂ , ... son los valores deseados de las neuronas de salida, es decir, las neuronas en la última capa, y un ^L ₁ , un ^L ₂ , ... son los valores de salida en sí mismos. Entonces, la entropía cruzada se puede definir como:

$$

$$C = - \ frac {1} {n} \ sum_x \ sum_j \ left [y_j \ ln a ^ L_j + (1-y_j) \ ln (1-a ^ L_j) \ right] \ tag {63}$$

Esto es lo mismo que la ecuación (57), solo que ahora nuestro ∑ _j suma todas las neuronas de salida. No analizaré la derivada en detalle, pero es razonable suponer que usando la expresión (63) podemos evitar la desaceleración en redes con muchas neuronas. Si está interesado, puede tomar la derivada en el siguiente problema.

Por cierto, el término "entropía cruzada" que uso confundió a algunos de los primeros lectores del libro porque contradice otras fuentes. En particular, a menudo la entropía cruzada se determina para dos distribuciones de probabilidad, pj
y qj, como ∑ _j p _j lnq _j . Esta definición puede asociarse con (57), si se considera que una neurona sigmoidea emite una distribución de probabilidad que consiste en la activación de la neurona ay su valor complementario 1-a.

Sin embargo, si tenemos muchas neuronas sigmoides en la última capa, el vector a ^L _j generalmente no proporciona una distribución de probabilidad. Como resultado, la definición del tipo ∑ _j p _j lnq _{j no tiene} sentido, ya que no trabajamos con distribuciones de probabilidad. En cambio (63), uno puede imaginar cómo se resume un conjunto sumado de entropías cruzadas de cada neurona, donde la activación de cada neurona se interpreta como parte de una distribución de probabilidad de dos elementos (por supuesto, no hay elementos probabilísticos en nuestras redes, por lo que en realidad no son probabilidades). En este sentido, (63) será una generalización de la entropía cruzada para distribuciones de probabilidad.

¿Cuándo usar la entropía cruzada en lugar del valor cuadrático? De hecho, la entropía cruzada casi siempre se usará mejor si tiene neuronas de salida sigmoideas. Para comprender esto, recuerde que al configurar una red, generalmente inicializamos pesos y compensaciones utilizando algún proceso aleatorio. Puede suceder que esta elección conduzca al hecho de que la red interpretará erróneamente algunos datos de entrada de entrenamiento; por ejemplo, la neurona de salida tenderá a 1, cuando debería ir a 0, o viceversa. Si usamos un valor cuadrático que ralentiza el entrenamiento, no se detendrá en absoluto, ya que los pesos continuarán siendo entrenados en otros ejemplos de entrenamiento, pero esta situación es obviamente indeseable.

Ejercicios

• Una trampa de la entropía cruzada es que al principio puede ser difícil recordar los roles correspondientes de y y a. Es fácil confundirse, ya que será correcto, - [ylna + (1 - y) ln (1 - a)] o - [alny + (1 - a) ln (1 - y)]. ¿Qué pasará con la segunda expresión cuando y = 0 o 1? ¿Este problema afecta a la primera expresión? Por qué
• En la discusión de una sola neurona al comienzo de la sección, dije que la entropía cruzada es pequeña si σ (z) ≈y para todos los datos de entrada de entrenamiento. , y 0 1. , (, ) y 0 1. , , σ(z)=y . ,

  $$

  $$C = -\frac{1}{n} \sum_x [y \ln y+(1-y) \ln(1-y)] \tag{64}$$
  . −[ylny+(1−y)ln(1−y)] .

• . ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \sigma'(z^L_j) \tag{65}$$
  σ'(z ^L _j ) , . , δ ^L x

  $$

  $$\delta^L = a^L-y \tag{66}$$
  , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{67}$$
  σ'(z ^L _j ) , , , . . , .
• . , . , , , , a ^L _j = z ^L _j . , δL x

  $$

  $$\delta^L = a^L-y \tag{68}$$
  , , , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{69}$$

  $$

  $$\frac{\partial C}{\partial b^L_{j}} = \frac{1}{n} \sum_x (a^L_j-y_j) \tag{70}$$
  , , . .

MNIST

La entropía cruzada es fácil de implementar como parte de un programa que enseña a la red utilizando el gradiente descendente y la propagación inversa. Haremos esto más adelante desarrollando una versión mejorada de nuestro programa de clasificación numérica manuscrita inicial de MNIST, network.py. El nuevo programa se llama network2.py e incluye no solo la entropía cruzada, sino también varias otras técnicas desarrolladas en este capítulo. Mientras tanto, veamos qué tan bien nuestro nuevo programa clasifica los dígitos MNIST. Como en el Capítulo 1, utilizaremos una red con 30 neuronas ocultas y un mini paquete de tamaño 10. Estableceremos la velocidad de aprendizaje η = 0.5 y aprenderemos 30 eras.

Como ya dije, es imposible decir exactamente qué velocidad de entrenamiento es adecuada en ese caso, así que experimenté con la selección. Es cierto que hay una manera de relacionar de manera muy heurística la tasa de aprendizaje con la entropía cruzada y el valor cuadrático. Vimos anteriormente que en los términos del gradiente para el valor cuadrático hay un término adicional σ '= σ (1-σ). Supongamos que promediamos estos valores para σ, ∫ ¹ ₀ dσ σ (1 - σ) = 1/6. Se puede ver que el costo cuadrático (más o menos) en promedio aprende 6 veces más lento para la misma tasa de aprendizaje. Esto sugiere que un buen punto de partida sería dividir la velocidad de aprendizaje para una función cuadrática por 6. Por supuesto, este no es un argumento estricto, y no debe tomarlo demasiado en serio. Pero a veces puede ser útil como punto de partida.

La interfaz para network2.py es ligeramente diferente de network.py, pero aún debe quedar claro lo que está sucediendo. La documentación en network2.py se puede obtener utilizando el comando de ayuda (network2.Network.SGD) en el shell de Python.

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True) 

Tenga en cuenta, por cierto, que el comando net.large_weight_initializer () se usa para inicializar pesos y compensaciones de la misma manera que se describe en el capítulo 1. Necesitamos ejecutarlo porque cambiaremos la inicialización de pesos por defecto más adelante. Como resultado, después de iniciar todos los comandos anteriores, obtenemos una red que funciona con una precisión del 95,49%. Esto está muy cerca del resultado del primer capítulo, 95.42%, usando el valor cuadrático.

Veamos también el caso en el que usamos 100 neuronas ocultas y entropía cruzada, y dejamos el resto igual. En este caso, la precisión es del 96.82%. Esta es una mejora importante sobre los resultados del primer capítulo, donde logramos una precisión del 96.59% utilizando el valor cuadrático. El cambio puede parecer pequeño, pero piense que el error cayó del 3.41% al 3.18%. Es decir, hemos eliminado aproximadamente 1/14 de errores. Esto es bastante bueno

Es bastante bueno que la función de costo de entropía cruzada nos dé resultados similares o mejores en comparación con el valor cuadrático. Sin embargo, no prueban inequívocamente que la entropía cruzada es la mejor opción. El hecho es que no intenté elegir hiperparámetros en absoluto: la velocidad del entrenamiento, el tamaño del mini-paquete, etc. Para que la mejora sea más convincente, debemos abordar adecuadamente su optimización. Pero los resultados siguen siendo inspiradores, y nuestros cálculos teóricos confirman que la entropía cruzada es una mejor opción que la función de costo cuadrático.

En este sentido, todo este capítulo y, en principio, el resto del libro pasará. Desarrollaremos nueva tecnología, la probaremos y obtendremos "mejores resultados". Por supuesto, es bueno que veamos estas mejoras. Pero interpretarlos siempre es difícil. Solo será convincente si vemos mejoras después de un trabajo serio en la optimización de todos los demás hiperparámetros. Y este es un trabajo bastante complicado, que requiere grandes recursos computacionales, y generalmente no trataremos con una investigación tan exhaustiva. En cambio, iremos más lejos en base a pruebas informales, como las enumeradas anteriormente. Pero debe tener en cuenta que tales pruebas no son evidencia inequívoca, y vigilar cuidadosamente esos casos cuando los argumentos comienzan a fallar.

Hasta ahora, hemos estado discutiendo la entropía cruzada en detalle. ¿Por qué desperdiciar tanto esfuerzo si da una mejora tan pequeña en nuestros resultados de MNIST? Más adelante en este capítulo veremos otras técnicas, en particular la regularización, que ofrecen mejoras mucho más fuertes. Entonces, ¿por qué nos centramos en la entropía cruzada? En particular, debido a que la entropía cruzada es una función de valor utilizada con frecuencia, por lo que vale la pena entenderlo bien. Pero la razón más importante es que la saturación de las neuronas es un problema importante en el campo de las redes neuronales, al que volveremos constantemente a lo largo del libro. Por lo tanto, discutí la entropía cruzada con tanto detalle, ya que es un buen laboratorio para comenzar a comprender la saturación de las neuronas y cómo abordar los enfoques para este problema.

¿Qué significa entropía cruzada? De donde viene

Nuestra discusión sobre la entropía cruzada giraba en torno al análisis algebraico y la implementación práctica. Esto es útil, pero como resultado, las preguntas conceptuales más amplias permanecen sin respuesta, por ejemplo: ¿qué significa entropía cruzada? ¿Hay una forma intuitiva de presentarlo? ¿Cómo podrían las personas llegar a la entropía cruzada?

Comencemos con el último: ¿qué podría hacernos pensar en la entropía cruzada? Supongamos que descubrimos una desaceleración del aprendizaje descrita anteriormente y nos dimos cuenta de que fue causada por los términos σ '(z) en las ecuaciones (55) y (56). Si echamos un vistazo a estas ecuaciones, podríamos pensar si es posible elegir dicha función de costo para que el término σ '(z) desaparezca. Entonces el costo C = C _{x de} un ejemplo de entrenamiento satisfaría las ecuaciones:

$$

$$\ frac {\ partial C} {\ partial w_j} = x_j (a-y) \ tag {71}$$

$$

$$\ frac {\ partial C} {\ partial b} = (a-y) \ tag {72}$$

Si elegimos una función de valor que los haga verdaderos, preferirían simplemente describir una comprensión intuitiva de que cuanto mayor es el error inicial, más rápido aprende la neurona. También solucionarían el problema de desaceleración. De hecho, comenzando con estas ecuaciones, mostraríamos que es posible derivar la forma de entropía cruzada simplemente siguiendo un instinto matemático. Para ver esto, notamos que, según la regla de la cadena, obtenemos:

$$

$$\ frac {\ partial C} {\ partial b} = \ frac {\ partial C} {\ partial a} \ sigma '(z) \ tag {73}$$

Usando en la última ecuación σ ′ (z) = σ (z) (1 - σ (z)) = a (1 - a), obtenemos:

$$

$$\ frac {\ partial C} {\ partial b} = \ frac {\ partial C} {\ partial a} a (1-a) \ tag {74}$$

Comparando con la ecuación (72), obtenemos:

$$

$$\ frac {\ partial C} {\ partial a} = \ frac {a-y} {a (1-a)} \ tag {75}$$

Al integrar esta expresión sobre a, obtenemos:

$$

$$C = - [y \ ln a + (1-y) \ ln (1-a)] + {\ rm constante} \ tag {76}$$

Esta es la contribución de un ejemplo de capacitación por separado x a la función de costo. Para obtener la función de costo total, necesitamos promediar todos los ejemplos de capacitación, y llegamos a:

$$

$$C = - \ frac {1} {n} \ sum_x [y \ ln a + (1-y) \ ln (1-a)] + {\ rm constante} \ tag {77}$$

La constante aquí es el promedio de las constantes individuales de cada uno de los ejemplos de entrenamiento. Como puede ver, las ecuaciones (71) y (72) determinan de forma única la forma de la entropía cruzada, carne a constante constante. La entropía cruzada no fue mágicamente sacada del aire. Ella podría ser encontrada de una manera simple y natural.

¿Qué pasa con la idea intuitiva de la entropía cruzada? ¿Cómo lo imaginamos? Una explicación detallada nos llevaría a adelantar nuestro curso de capacitación. Sin embargo, podemos mencionar la existencia de una forma estándar de interpretar la entropía cruzada, que se origina en el campo de la teoría de la información. En términos generales, la entropía cruzada es una medida de sorpresa. Por ejemplo, nuestra neurona está tratando de calcular la función x → y = y (x). Pero en cambio, cuenta la función x → a = a (x). Supongamos que imaginamos a como una estimación de la neurona de la probabilidad de que y = 1, y 1-a es la probabilidad de que el valor correcto para y sea 0. Luego, la entropía cruzada mide cuánto estamos "sorprendidos", en promedio, cuando encuentra el verdadero valor de y. No estamos muy sorprendidos si esperamos una salida, y estamos muy sorprendidos si la salida es inesperada. Por supuesto, no di una definición estricta de "sorpresa", por lo que todo esto puede parecer una diatriba vacía. Pero, de hecho, en la teoría de la información hay una forma exacta de determinar lo inesperado. Desafortunadamente, no conozco ningún ejemplo de una discusión buena, corta y autosuficiente de este punto en Internet. Pero si está interesado en profundizar un poco más, entonces el artículo de Wikipedia tiene buena información general que lo enviará en la dirección correcta. Los detalles se pueden encontrar en el Capítulo 5 sobre la desigualdad de Kraft en un libro sobre teoría de la información .

Desafío

• Hemos discutido en detalle la desaceleración en el aprendizaje que puede ocurrir cuando las neuronas están saturadas en las redes que utilizan la función de costo cuadrático en el aprendizaje. Otro factor que puede inhibir el aprendizaje es la presencia del término x _j en la ecuación (61). Por eso, cuando la salida x _{j se} aproxima a cero, el peso correspondiente w _j se entrenará lentamente. Explique por qué es imposible eliminar el término x _j eligiendo alguna función de costo ingeniosa.

Softmax (función máxima suave)

En este capítulo, usaremos principalmente la función de costo de entropía cruzada para resolver los problemas de desaceleración del aprendizaje. Sin embargo, me gustaría discutir brevemente otro enfoque para este problema, basado en el llamado softmax-capas de neuronas. No usaremos capas Softmax para el resto de este capítulo, por lo que si tiene prisa, puede omitir esta sección. Sin embargo, todavía vale la pena entender Softmax, en particular porque es interesante en sí mismo, y en particular porque usaremos capas Softmax en el Capítulo 6, en nuestra discusión sobre redes neuronales profundas.

La idea de Softmax es definir un nuevo tipo de capa de salida para HC. Comienza de la misma manera que la capa sigmoidea, con la formación de entradas ponderadas. $$$z ^ L_j = \ sum_ {k} w ^ L_ {jk} a ^ {L-1} _k + b ^ L_j$ . Sin embargo, no utilizamos un sigmoide para obtener una respuesta. En la capa Softmax, aplicamos la función Softmax a z ^L _j . Según ella, la activación a ^L _{j de la} neurona de salida No. j es igual a:

$$

$$a ^ L_j = \ frac {e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} \ tag {78}$$

donde en el denominador sumamos todas las neuronas de salida.

Si la función Softmax no le resulta familiar, la ecuación (78) le parecerá misteriosa. No es del todo obvio por qué deberíamos usar tal función. Tampoco es obvio que nos ayudará a resolver el problema de ralentizar el aprendizaje. Para comprender mejor la ecuación (78), supongamos que tenemos una red con cuatro neuronas de salida y cuatro entradas ponderadas correspondientes, que designaremos como z ^L ₁ , z ^L ₂ , z ^L ₃ y z ^L ₄ . El artículo original contiene controles deslizantes de ajuste interactivo, a los que se les asignan los valores posibles de las entradas ponderadas y la programación de las activaciones de salida correspondientes. Un buen punto de partida para estudiarlos sería usar el control deslizante inferior para aumentar z ^L ₄ .





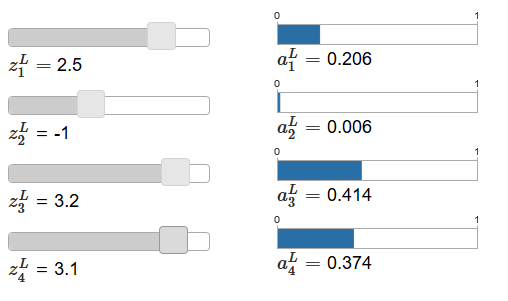
Al aumentar z ^L ₄ , se puede observar un aumento en la activación de salida correspondiente, un ^L ₄ y una disminución en otras activaciones de salida. Al disminuir z ^L ₄ a ^L ₄ disminuirá, y todas las demás activaciones de salida aumentarán. Después de mirar de cerca, verá que en ambos casos el cambio general en otras activaciones compensa exactamente el cambio que ocurre en un ^L ₄ . La razón de esto es la garantía de que todas las activaciones de salida en total dan 1, que podemos probar usando la ecuación (78) y algo de álgebra:

$$

$$\ sum_j a ^ L_j = \ frac {\ sum_j e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} = 1 \ tag {79}$$

Como resultado, con un aumento de ^L ₄ , las activaciones de salida restantes deben disminuir en el mismo valor en total para garantizar que la suma de todas las activaciones de salida sea igual a 1. Y, por supuesto, declaraciones similares serán ciertas para todas las demás activaciones.

También se deduce de la ecuación (78) que todas las activaciones de salida son positivas, ya que la función exponencial es positiva. Combinando esto con la observación de la sección anterior, encontramos que la salida de la capa Softmax es un conjunto de números positivos que dan un total de 1. En otras palabras, la salida de la capa Softmax se puede representar como una distribución de probabilidad.

El hecho de que la salida de la capa Softmax es una distribución de probabilidad es muy agradable. En muchos problemas, es conveniente poder interpretar las activaciones de salida a ^L _j como una estimación por la red de la probabilidad de que el bulet j sea la opción correcta. Entonces, por ejemplo, en el problema de clasificación MNIST, podemos interpretar un ^L _j como una estimación por la red de la probabilidad de que j sea la versión correcta de la clasificación de un dígito.

Por el contrario, si la capa de salida era sigmoidea, definitivamente no podemos suponer que las activaciones forman una distribución de probabilidad. No probaré esto estrictamente, pero es razonable suponer que las activaciones de la capa sigmoidea en el caso general no forman una distribución de probabilidad. Por lo tanto, utilizando una capa de salida sigmoidea, no obtendremos una interpretación tan simple de las activaciones de salida.

Ejercicio

• Haga un ejemplo que muestre que en una red con una capa de salida sigmoidea, las activaciones de salida a ^L _j no siempre suman 1.

Comenzamos a entender un poco sobre las funciones de Softmax y cómo se comportan las capas de Softmax. Solo para resumir: los exponentes en la ecuación (78) aseguran que todas las activaciones de salida sean positivas. La suma en el denominador de la ecuación (78) asegura que Softmax da un total de 1. Por lo tanto, este tipo de ecuación ya no parece misteriosa: esta es una forma natural de garantizar que las activaciones de salida formen una distribución de probabilidad. Softmax se puede imaginar como una forma de escalar z ^L _j y luego comprimirlos para formar una distribución de probabilidad.

Ejercicios

• La monotonía de Softmax. Demuestre que ∂a ^L _j / ∂z ^L _{k es} positivo si j = k, y negativo si j ≠ k. Como resultado, _se garantiza que un aumento en z ^L _j aumentará la activación de salida correspondiente a ^L _j , y disminuirá todas las demás activaciones de salida. Ya hemos visto esto empíricamente usando el ejemplo de controles deslizantes, pero esta prueba será rigurosa.
• No localidad Softmax. Una buena característica de las capas sigmoideas es que la salida a ^L _j es una función de la entrada ponderada correspondiente, a ^L _j = σ (z ^L _j ). Explique por qué este no es el caso con la capa Softmax: cualquier activación de salida a ^L _j depende de todas las entradas ponderadas.

Desafío

• Invierta la capa Softmax. Supongamos que tenemos un NS con una capa Softmax de salida y las activaciones a ^L _{j son} conocidas. Demuestre que las entradas ponderadas correspondientes tienen la forma z ^L _j = ln a ^L _j + C, donde C es una constante independiente de j.

Problema de desaceleración del aprendizaje

Ya nos hemos familiarizado bastante con las capas de neuronas Softmax. Pero hasta ahora no hemos visto cómo las capas Softmax nos permiten resolver el problema de ralentizar el aprendizaje. Para comprender esto, definamos una función de costo basada en la "probabilidad de registro". Usaremos x para denotar la entrada de entrenamiento de la red, e y para la salida deseada correspondiente. Entonces el LPS asociado con esta entrada de capacitación será:

$$

$$C \ equiv - \ ln a ^ L_y \ tag {80}$$

Entonces, si, por ejemplo, estudiamos en imágenes MNIST, y la imagen 7 entró en la entrada, entonces el LPS será −ln un ^L ₇ . Para entender esto intuitivamente, consideramos el caso cuando la red maneja bien el reconocimiento, es decir, está seguro de que está en la entrada 7. En este caso, evaluará el valor de la probabilidad correspondiente a ^L ₇ como cercano a 1, por lo tanto, el costo −ln a ^L ₇ será pequeño . Por el contrario, si la red no funciona bien, entonces la probabilidad de un ^L ₇ será menor, y el costo −ln un ^L ₇ será mayor. Por lo tanto, LPS se comporta como se espera de una función de costo.

¿Qué pasa con el problema de desaceleración? Para analizarlo, recordamos que lo principal en la desaceleración es el comportamiento de ∂C / ∂w ^L _jk y ∂C / ∂b ^L _j . No describiré en detalle la captura de la derivada; le pediré que haga esto en las tareas, pero utilizando algo de álgebra puede demostrar que:

$$

$$\ frac {\ partial C} {\ partial b ^ L_j} = a ^ L_j-y_j \ tag {81}$$

$$

$$\ frac {\ partial C} {\ partial w ^ L_ {jk}} = a ^ {L-1} _k (a ^ L_j-y_j) \ tag {82}$$

He jugado un poco con la notación aquí, y estoy usando "y" un poco diferente que en el último párrafo. Allí y denota la salida de red deseada, es decir, si la salida es "7", entonces la entrada era la imagen 7. Y en estas ecuaciones, y denota el vector de activación de salida correspondiente a 7, es decir, un vector que tiene todos ceros excepto la unidad en 7 th puesto.

Estas ecuaciones son las mismas que expresiones similares que obtuvimos en un análisis anterior de entropía cruzada. Compare, por ejemplo, las ecuaciones (82) y (67). Esta es la misma ecuación, aunque esta última se promedia sobre ejemplos de entrenamiento. Y, como en el primer caso, estas expresiones garantizan que el aprendizaje no se ralentiza. Es útil imaginar que la capa de Softmax de salida con LPS es bastante similar a la capa con salida sigmoidea y el costo basado en la entropía cruzada.

Dada su similitud, ¿qué se debe usar: salida sigmoidea y entropía cruzada, o salida Softmax y LPS? De hecho, en muchos casos ambos enfoques funcionan bien. Aunque más adelante en este capítulo usaremos una capa de salida sigmoidea con un costo basado en la entropía cruzada. Más adelante, en el capítulo 6, a veces usaremos la salida Softmax y LPS. La razón de los cambios es hacer que algunas de las siguientes redes sean más similares a las redes que se encuentran en algunos artículos de investigación influyentes. Desde un punto de vista más general, Softmax y LPS deben usarse cuando necesite interpretar las activaciones de salida como probabilidades. Esto no siempre es necesario, pero puede ser útil en problemas de clasificación (como MNIST), que incluyen clases que no se cruzan.

Las tareas

• Derive las ecuaciones (81) y (82).
• ¿De dónde viene el nombre Softmax? Supongamos que cambiamos la función Softmax para que las activaciones de salida estén dadas por la ecuación

  $$

  $$a ^ L_j = \ frac {e ^ {c z ^ L_j}} {\ sum_k e ^ {c z ^ L_k}} \ tag {83}$$
  donde c es una constante positiva. Tenga en cuenta que c = 1 corresponde a la función estándar de Softmax. Pero usando un valor diferente de c, obtenemos otra función que seguirá siendo cualitativamente similar a Softmax. Muestre que las activaciones de salida forman una distribución de probabilidad, como es el caso con Softmax regular. Supongamos que hacemos c muy grande, es decir, c → & inf;. ¿Cuál es el valor límite de las activaciones de salida a ^L _j ? Después de resolver este problema, debe quedar claro por qué una función con c = 1 se considera una "versión suavizada" de la función máxima. De aquí proviene el término softmax.
• Propagación hacia atrás con Softmax y LPS. En el último capítulo, derivamos el algoritmo de retropropagación para una red que contiene capas sigmoideas. Para aplicar este algoritmo a las capas de red y Softmax, necesitamos derivar la expresión para el error δ ^L _j ≡ ∂C / ∂z ^L _j . Demuestre que una expresión adecuada sería

  $$

  $$\ delta ^ L_j = a ^ L_j -y_j \ tag {84}$$
  Usando esta expresión, podemos aplicar el algoritmo de retropropagación a la red usando la capa de salida Softmax y LPS.

Reciclaje y regularización

Una vez se le pidió al premio Nobel Enrico Fermi una opinión sobre el modelo matemático propuesto por varios colegas para resolver un importante problema físico no resuelto. El modelo correspondía perfectamente al experimento, pero Fermi se mostró escéptico al respecto. Preguntó cuántos parámetros libres se pueden cambiar. "Cuatro", le dijeron. Fermi respondió: "Recuerdo que a mi amigo Johnny von Neumann le gustaba decir que con cuatro parámetros puedes empujar a un elefante allí, y con cinco puedes hacer que agite su trompa".

El significado de la historia, por supuesto, es que los modelos con una gran cantidad de parámetros libres pueden describir una gama sorprendentemente amplia de fenómenos.Incluso si dicho modelo funciona bien con los datos disponibles, no lo convierte automáticamente en un buen modelo. Simplemente podría significar que el modelo tiene suficiente libertad para describir casi cualquier conjunto de datos de un tamaño determinado sin revelar la idea principal del fenómeno. Cuando esto sucede, el modelo funciona bien con los datos existentes, pero no puede generalizar la nueva situación. Una verdadera prueba de un modelo es su capacidad para hacer predicciones en situaciones que no ha encontrado antes.

Fermi y von Neumann sospechaban de modelos con cuatro parámetros. ¡Nuestro NS con 30 neuronas ocultas para la clasificación de dígitos MNIST tiene casi 24,000 parámetros! Estos son bastantes parámetros. Nuestro NS con 100 neuronas ocultas tiene casi 80,000 parámetros, y los NS profundos avanzados de estos parámetros a veces tienen millones o incluso miles de millones. ¿Podemos confiar en los resultados de su trabajo?

Vamos a complicar este problema creando una situación en la que nuestra red generalice mal una nueva situación para ella. Usaremos NS con 30 neuronas ocultas y 23.860 parámetros. Pero no entrenaremos la red con las 50,000 imágenes MNIST. En cambio, usamos solo los primeros 1000. El uso de un conjunto limitado hará que el problema de generalización sea más obvio. Estudiaremos como antes, utilizando la función de costo basada en la entropía cruzada, con una velocidad de aprendizaje de η = 0.5 y un tamaño de mini paquete de 10. Sin embargo, estudiaremos 400 eras, que es un poco más que antes, ya que hay ejemplos de capacitación no tenemos mucho Usemos network2 para ver cómo cambia la función de costo:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True, monitor_training_cost=True) 

Usando los resultados, podemos construir un gráfico del cambio en el costo al entrenar la red (los gráficos se hicieron usando el programa overfitting.py):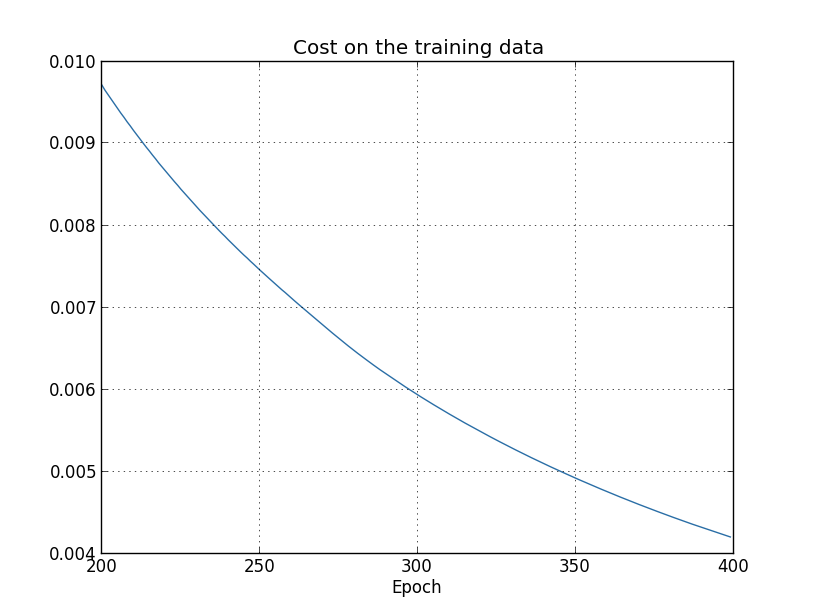



parece alentador, hay una disminución suave en el costo, como se esperaba. Tenga en cuenta que solo mostré las épocas de 200 a 399. Como resultado, vemos a mayor escala las etapas tardías del entrenamiento, en las cuales, como veremos más adelante, suceden todas las cosas más interesantes.

Ahora veamos cómo la precisión de clasificación en los datos de verificación cambia con el tiempo:



Luego volví a aumentar el horario. En las primeras 200 eras, que no son visibles aquí, la precisión aumenta a casi el 82%. Luego, el entrenamiento se ralentiza gradualmente. Finalmente, alrededor de la era 280, la precisión de la clasificación deja de mejorar. En épocas posteriores, solo se observan pequeñas fluctuaciones estocásticas en torno al valor de precisión alcanzado en la 280ª época. Compare esto con el gráfico anterior, donde el costo asociado con los datos de capacitación está disminuyendo gradualmente. Si estudia solo este costo, parecerá que el modelo está mejorando. Sin embargo, los resultados de trabajar con datos de prueba nos dicen que esta mejora es solo una ilusión. Como en el modelo que a Fermi no le gustó, lo que nuestra red estudia después de la era 280 ya no se generaliza a los datos de verificación. Por lo tanto, este entrenamiento deja de ser útil. Decimos que después de la era 280, la red se está volviendo a capacitar,o sobreajuste.

Puede que se pregunte si no es un problema que esté estudiando el costo en función de los datos de capacitación y no en la precisión de la clasificación de los datos de verificación. En otras palabras, quizás el problema es que estamos comparando manzanas con naranjas. ¿Qué sucederá si comparamos el costo de los datos de capacitación con el costo de la verificación, es decir, compararemos medidas comparables? ¿O tal vez podríamos comparar la precisión de clasificación de los datos de entrenamiento y prueba? De hecho, el mismo fenómeno aparece independientemente de cómo se haga la comparación. Pero los detalles están cambiando. Por ejemplo, veamos el valor de los datos de verificación:



Se puede ver que el costo de los datos de verificación mejora hasta alrededor de la 15a era, y luego comienza a deteriorarse por completo, aunque el costo de los datos de capacitación continúa mejorando. Esta es otra señal de un modelo reentrenado. Sin embargo, surge la pregunta: ¿en qué época deberíamos considerar el punto en el que el reciclaje comienza a prevalecer sobre el entrenamiento: 15 o 280? Desde un punto de vista práctico, sin embargo, estamos interesados ​​en mejorar la precisión de la clasificación de los datos de verificación, y el costo es solo un mediador de la precisión de la clasificación. Por lo tanto, tiene sentido considerar la era de 280 por punto, después de lo cual el reciclaje comienza a prevalecer sobre el entrenamiento de nuestra Asamblea Nacional.

Otro signo de reciclaje puede verse en la precisión de la clasificación de los datos de entrenamiento:



La precisión está creciendo, llegando al 100%. Es decir, nuestra red clasifica correctamente las 1000 imágenes de entrenamiento. Mientras tanto, la precisión de la verificación crece a solo 82.27%. Es decir, nuestra red solo estudia las características del conjunto de entrenamiento y no aprende a reconocer números en absoluto. Parece que la red simplemente recuerda el conjunto de entrenamiento, sin entender los números lo suficientemente bien como para generalizar esto al conjunto de prueba.

La reentrenamiento es un problema grave de la Asamblea Nacional. Esto es especialmente cierto para los NS modernos, que generalmente tienen una gran cantidad de pesos y desplazamientos. Para un entrenamiento efectivo, necesitamos una forma de determinar cuándo ocurre el reciclaje para no volver a entrenar. Y también nos gustaría poder reducir los efectos del reciclaje.

Una forma obvia de detectar el reentrenamiento es utilizar el enfoque anterior, monitorear la precisión del trabajo con datos de verificación durante el entrenamiento en red. Si vemos que la precisión de los datos de verificación ya no mejora, debemos dejar de entrenar. Por supuesto, estrictamente hablando, esto no será necesariamente una señal de reciclaje. Quizás la precisión de trabajar con pruebas y datos de entrenamiento dejará de mejorar al mismo tiempo. Sin embargo, la aplicación de dicha estrategia evitará la reentrenamiento.

Y usaremos una pequeña variación de esta estrategia. Recuerde que cuando cargamos datos en MNIST, los dividimos en tres conjuntos:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Hasta ahora hemos utilizado training_data y test_data, y hemos ignorado validation_data [confirmando]. Validation_data contiene 10,000 imágenes, que difieren de las 50,000 imágenes del conjunto de entrenamiento MNIST y las 10,000 imágenes del conjunto de validación. En lugar de usar test_data para evitar el sobreajuste, usaremos validation_data. Para hacer esto, usaremos casi la misma estrategia que se describió anteriormente para test_data. Es decir, calcularemos la precisión de clasificación de validation_data al final de cada era. Una vez que la precisión de clasificación de validation_data esté completa, dejaremos de aprender. Esta estrategia se llama una parada temprana. Por supuesto, en la práctica, no podremos descubrir de inmediato que la precisión está saciada. En cambio, continuaremos entrenando hasta que nos aseguremos de esto (y decidamoscuando necesita detenerse, no siempre es fácil, y puede usar enfoques más o menos agresivos para esto).

¿Por qué usar validation_data para evitar el reentrenamiento en lugar de test_data? Es parte de una estrategia más general usar validation_data para evaluar diferentes opciones para hiperparámetros: la cantidad de épocas para aprender, la velocidad de aprendizaje, la mejor arquitectura de red, etc. Utilizamos estas estimaciones para encontrar y asignar buenos valores a los hiperparámetros. Y aunque todavía no he mencionado esto, fue en parte debido a esto que elegí los hiperparámetros en los ejemplos anteriores del libro.

Por supuesto, este comentario no responde a la pregunta de por qué usamos validation_data, y no test_data, para evitar el sobreajuste. Simplemente reemplaza la respuesta a una pregunta más general: ¿por qué usamos validation_data, y no test_data, para seleccionar hiperparámetros? Para comprender esto, tenga en cuenta que al elegir hiperparámetros, lo más probable es que tengamos que elegir entre una variedad de sus opciones. Si asignamos hiperparámetros basados ​​en las calificaciones de test_data, probablemente adaptaremos estos datos demasiado específicamente para test_data. Es decir, podemos encontrar hiperparámetros que se adaptan bien a las características específicas de datos específicos de test_data, sin embargo, el funcionamiento de nuestra red no se generalizará a otros conjuntos de datos. Evitamos esto seleccionando hiperparámetros usando validation_data. Y luego, habiendo recibido el GP que necesitamos,Realizamos una evaluación final de precisión utilizando test_data. Esto nos da la confianza de que nuestros resultados con test_data son una verdadera medida del grado de generalización del NS. En otras palabras, los datos de respaldo son datos de entrenamiento tan especiales que nos ayudan a aprender un buen GP. Este enfoque para localizar GPs a veces se llama método de retención, ya que validation_data se "mantiene" por separado de training_data.

En la práctica, incluso después de evaluar la calidad del trabajo en test_data, querremos cambiar de opinión e intentar un enfoque diferente, tal vez una arquitectura de red diferente, que incluirá búsquedas de un nuevo conjunto de GP. En este caso, ¿existe el peligro de que nos adaptemos innecesariamente a test_data? ¿Necesitaremos un número potencialmente infinito de conjuntos de datos para poder estar seguros de que nuestros resultados están bien generalizados? En general, este es un problema profundo y complejo. Pero para nuestros propósitos prácticos, no nos preocuparemos demasiado por esto. Simplemente nos sumergimos de lleno en nuevas investigaciones utilizando un método de retención simple basado en training_data, validation_data y test_data, como se describió anteriormente.

Hasta ahora, hemos estado considerando la reentrenamiento con 1000 imágenes de entrenamiento. ¿Qué sucede si utilizamos un conjunto completo de capacitación de 50,000 imágenes? Dejaremos los demás parámetros sin cambios (30 neuronas ocultas, velocidad de aprendizaje 0.5, tamaño mini-paquete 10), pero estudiaremos 30 eras usando las 50,000 imágenes. Aquí hay un gráfico que muestra la precisión de la clasificación en datos de entrenamiento y datos de prueba. Tenga en cuenta que aquí utilicé datos de validación en lugar de datos de validación para que sea más fácil comparar los resultados con gráficos anteriores.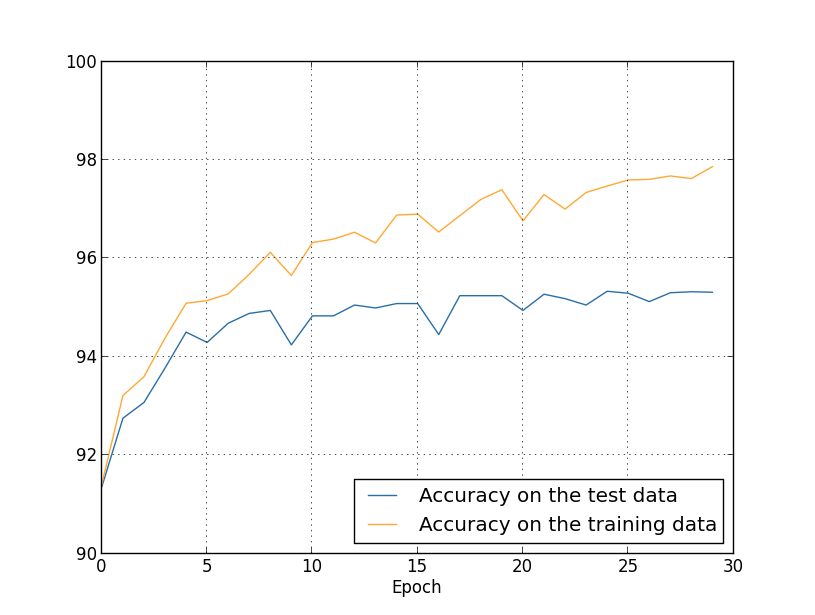



Se puede ver que los indicadores de precisión en la prueba y los datos de entrenamiento permanecen más cerca uno del otro que cuando se usan 1000 ejemplos de entrenamiento. En particular, la mejor precisión de clasificación, 97.86%, es solo 2.53% mayor que el 95.33% de los datos de verificación. ¡Compare con un descanso temprano del 17.73%! Se está llevando a cabo una nueva capacitación, pero se ha reducido considerablemente. Nuestra red recopila información mucho mejor, pasando de la capacitación a los datos de prueba. En general, una de las mejores formas de reducir el reciclaje es aumentar la cantidad de datos de entrenamiento. Con suficientes datos de entrenamiento, es difícil volver a capacitar incluso una red muy grande. Desafortunadamente, obtener datos de capacitación es costoso y / o difícil, por lo que esta opción no siempre es práctica.

Regularización

Aumentar la cantidad de datos de entrenamiento es una forma de reducir el reciclaje. ¿Hay otras formas de reducir el reciclaje? Un posible enfoque es reducir el tamaño de la red. Es cierto que las redes grandes tienen potencial más que las pequeñas, por lo que somos reacios a recurrir a esta opción.

Afortunadamente, existen otras técnicas que pueden reducir el reciclaje, incluso cuando hemos arreglado el tamaño de la red y los datos de entrenamiento. Se conocen como técnicas de regularización. En este capítulo, describiré una de las técnicas más populares, a veces llamadas pesas de debilitamiento o regularización de L2. Su idea es agregar un miembro adicional llamado miembro de regularización a la función de costo. Aquí hay entropía cruzada con regularización:

$$

$$C = -\frac{1}{n} \sum_{xj} \left[ y_j \ln a^L_j+(1-y_j) \ln (1-a^L_j)\right] + \frac{\lambda}{2n} \sum_w w^2 \tag{85}$$

El primer término es una expresión común para entropía cruzada. Pero agregamos un segundo, a saber, la suma de los cuadrados de todos los pesos de la red. Se escala por el factor λ / 2n, donde λ> 0 es el parámetro de regularización yn, como de costumbre, es el tamaño del conjunto de entrenamiento. Discutiremos cómo elegir λ. También vale la pena señalar que los sesgos no están incluidos en el término de regularización. Sobre esto a continuación.

Por supuesto, es posible regularizar otras funciones de costo, por ejemplo, cuadrático. Esto se puede hacer de manera similar:

$$

$$C = \frac{1}{2n} \sum_x \|y-a^L\|^2 + \frac{\lambda}{2n} \sum_w w^2 \tag{86}$$

En ambos casos, podemos escribir la función de costo regularizado como

$$

$$C = C_0 + \frac{\lambda}{2n} \sum_w w^2 \tag{87}$$

donde C ₀ es la función de costo original sin regularización.

Es intuitivamente claro que el objetivo de la regularización es persuadir a la red para que prefiera pesos más pequeños, en igualdad de condiciones. Los pesos grandes solo serán posibles si mejoran significativamente la primera parte de la función de costo. En otras palabras, la regularización es una forma de elegir un compromiso entre encontrar pesos pequeños y minimizar la función de costo inicial. Es importante que estos dos elementos del compromiso dependan del valor de λ: cuando λ es pequeño, preferimos minimizar la función de costo original, y cuando λ es grande, preferimos pesos pequeños.

¡No es del todo obvio por qué la elección de tal compromiso debería ayudar a reducir el reciclaje! Pero resulta que ayuda. Averiguaremos por qué ayuda en la siguiente sección. Pero primero, trabajemos con un ejemplo que muestre que la regularización reduce el reciclaje.

Para construir un ejemplo, primero debemos entender cómo aplicar el algoritmo de entrenamiento con descenso de gradiente estocástico a un NS regularizado. En particular, necesitamos saber cómo calcular las derivadas parciales, ∂C / ∂w y ∂C / ∂b para todos los pesos y compensaciones en la red. Después de tomar las derivadas parciales en la ecuación (87) obtenemos:

$$

$$\frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w \tag{88}$$

$$

$$\frac{\partial C}{\partial b} = \frac{\partial C_0}{\partial b} \tag{89}$$

Los términos ∂C ₀ / ∂w y ∂C ₀ / ∂w se pueden calcular a través del OP, como se describe en el capítulo anterior. Vemos que es fácil calcular el gradiente de la función de costo regularizado: solo necesita usar el OP como de costumbre y luego agregar λ / nw a la derivada parcial de todos los términos de peso. Las derivadas parciales con respecto a los desplazamientos no cambian, por lo tanto, la regla de aprendizaje por descenso de gradiente para desplazamientos no difiere de la habitual:

$$

$$b \rightarrow b -\eta \frac{\partial C_0}{\partial b} \tag{90}$$

La regla de entrenamiento para pesas se convierte en:

$$

$$w \rightarrow w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda}{n} w \tag{91}$$

$$

$$= \left(1-\frac{\eta \lambda}{n}\right) w -\eta \frac{\partial C_0}{\partial w} \tag{92}$$

Todo es igual que en la regla de descenso de gradiente habitual, excepto que primero escalamos el peso w por un factor de 1 - ηλ / n. Esta escala a veces se llama pérdida de peso, ya que reduce el peso. A primera vista, parece que los pesos tienden irresistiblemente a cero. Pero esto no es así, ya que el otro término puede conducir a un aumento en los pesos si esto conduce a una disminución en la función de costo irregular.

Ok, deja que el descenso de gradiente funcione así. ¿Qué pasa con el descenso de gradiente estocástico? Bueno, como en la versión irregular del descenso de gradiente estocástico, podemos estimar ∂C ₀ / ∂w promediando sobre el mini paquete de ejemplos de entrenamiento m. Por lo tanto, la regla de aprendizaje regularizado para el descenso de gradiente estocástico se convierte en (ver ecuación (20)):

$$

$$w \rightarrow \left(1-\frac{\eta \lambda}{n}\right) w -\frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial w} \tag{93}$$

donde la suma va para los ejemplos de entrenamiento x en el mini paquete, y C _x es el costo irregular para cada ejemplo de entrenamiento. Todo es igual que en la regla habitual del descenso de gradiente estocástico, con la excepción de 1 - ηλ / n, el factor de pérdida de peso. Finalmente, para completar la imagen, permítanme escribir una regla regularizada para las compensaciones. Naturalmente, es exactamente lo mismo que en el caso irregular (ver ecuación (21)):

$$

$$b \rightarrow b - \frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial b} \tag{94}$$

donde va la cantidad para ejemplos de entrenamiento x en el mini-paquete.

Veamos cómo la regularización cambia la efectividad de nuestra Asamblea Nacional. Utilizaremos una red con 30 neuronas ocultas, un mini-paquete de tamaño 10, una velocidad de aprendizaje de 0.5 y una función de costo con entropía cruzada. Sin embargo, esta vez usamos el parámetro de regularización λ = 0.1. En el código, llamé a esta variable lmbda, ya que la palabra lambda está reservada en python para cosas que no están relacionadas con nuestro tema. También usé test_data nuevamente en lugar de validation_data. Pero decidí usar test_data, porque los resultados se pueden comparar directamente con nuestros primeros resultados irregulares. Puede cambiar fácilmente el código para que use validation_data y asegurarse de que los resultados sean similares.

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, ... evaluation_data=test_data, lmbda = 0.1, ... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True, ... monitor_training_cost=True, monitor_training_accuracy=True) 

El costo de los datos de entrenamiento disminuye constantemente, como en el caso inicial, sin regularización:



Pero esta vez, la precisión en test_data continúa aumentando a lo largo de las 400 eras: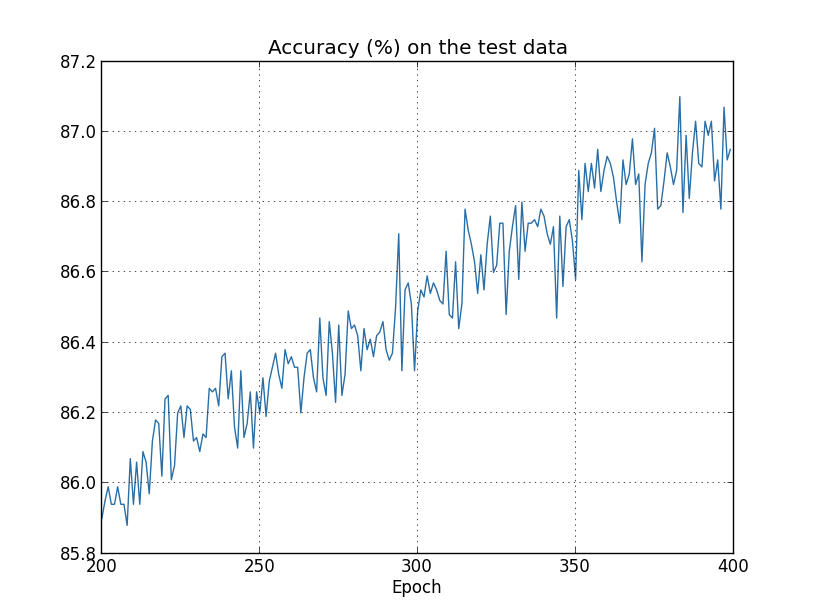



Obviamente, la regularización ha suprimido el reciclaje. Además, la precisión ha aumentado significativamente, y la precisión de clasificación de pico alcanza el 87.1%, en comparación con el pico de 82.27% alcanzado en el caso sin regularización. En general, es casi seguro que logremos mejores resultados al continuar estudiando después de 400 eras. Empíricamente, la regularización parece hacer que nuestra red generalice mejor el conocimiento y reduzca significativamente los efectos del reciclaje.

¿Qué sucede si dejamos nuestro entorno artificial, que usa solo 1,000 imágenes de enseñanza, y regresamos al conjunto completo de 50,000 imágenes? Por supuesto, ya hemos visto que el reentrenamiento es un problema mucho más pequeño con un conjunto completo de 50,000 imágenes. ¿La regularización ayuda a mejorar el resultado? Conservemos los valores anteriores de los hiperparámetros: 30 épocas, velocidad 0.5, tamaño mini-paquete 10. Sin embargo, necesitamos cambiar el parámetro de regularización. El hecho es que el tamaño n del conjunto de entrenamiento saltó de 1000 a 50 000, y esto cambia el factor de debilitamiento de los pesos 1 - ηλ / n. Si continuamos usando λ = 0.1, esto significaría que los pesos se debilitan mucho menos, y como resultado, el efecto de la regularización disminuye. Para compensar esto, aceptamos λ = 5.0.

Ok, entrenemos nuestra red reinicializando primero los pesos:

 >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, ... evaluation_data=test_data, lmbda = 5.0, ... monitor_evaluation_accuracy=True, monitor_training_accuracy=True) 

Obtenemos los resultados: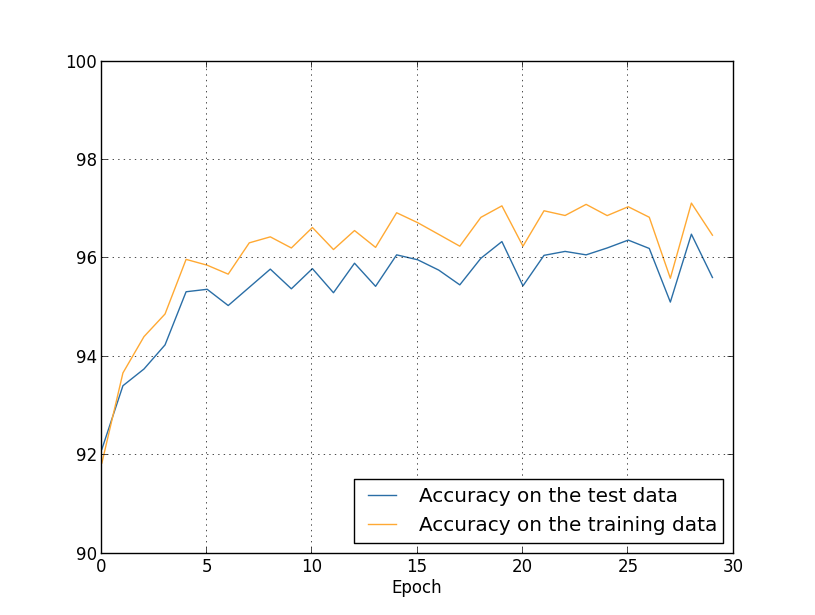



todo agradable. En primer lugar, nuestra precisión de clasificación en los datos de verificación ha crecido, de 95.49% sin regularización a 96.49% con regularización. Esta es una mejora importante. En segundo lugar, se puede ver que la brecha entre los resultados del trabajo en el entrenamiento y los conjuntos de pruebas es mucho menor que antes, menos del 1%. La brecha aún es decente, pero obviamente hemos logrado un progreso significativo en la reducción de la capacitación.

Finalmente, vea qué precisión de clasificación obtenemos cuando usamos 100 neuronas ocultas y el parámetro de regularización & lambda = 5.0. No daré un análisis detallado del reentrenamiento, esto es solo por diversión, para ver cuánta precisión se puede lograr con nuestros nuevos trucos: una función de costo con entropía cruzada y regularización de L2.

 >>> net = network2.Network([784, 100, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

El resultado final es una precisión de clasificación del 97,92% en los datos de respaldo. Un gran salto en comparación con el caso de 30 neuronas ocultas. Puede ajustar un poco más, iniciar el proceso durante 60 épocas con η = 0.1 y λ = 5.0, y superar la barrera del 98%, alcanzando una precisión de 98.04 en los datos de soporte. ¡No está mal para 152 líneas de código!

Describí la regularización como una forma de reducir el reciclaje y aumentar la precisión de la clasificación. Pero estas no son sus únicas ventajas. Empíricamente, después de haber intentado a través de muchos lanzamientos nuestra red MNIST, cambiando los pesos cada vez, descubrí que los lanzamientos sin regularización a veces "se atascaron", obviamente, cayendo en el mínimo local de la función de costo. Como resultado, diferentes lanzamientos a veces producen resultados muy diferentes. Y la regularización, por el contrario, le permite obtener resultados reproducibles mucho más fáciles.

¿Por qué es esto así? Heurísticamente, cuando la función de costo no tiene regularización, la longitud del vector de pesos probablemente crecerá, siendo todas las demás cosas iguales. Con el tiempo, esto puede conducir a un gran vector de pesos. Y debido a esto, el vector de las escalas puede atascarse, mostrándose en aproximadamente la misma dirección, ya que los cambios debidos al descenso del gradiente solo hacen pequeños cambios de dirección con una gran longitud del vector. Creo que debido a este fenómeno, es muy difícil para nuestro algoritmo de entrenamiento estudiar adecuadamente el espacio de las pesas y, por lo tanto, es difícil encontrar un buen mínimo de la función de costo.