Ruido en big data. Análisis de entropía

Encontré una tarea llamada Enscombe Quartet ( Anscombe ) ”( versión en inglés ).

La Figura 1 muestra una distribución tabular de 4 funciones aleatorias (tomadas de Wikipedia).


Fig. 1. Distribución de tablas de cuatro funciones aleatorias

La Figura 2 muestra los parámetros de distribución de estas funciones aleatorias.


Fig. 2. Parámetros de distribución de cuatro funciones aleatorias.

Y sus gráficos en la Figura 3.


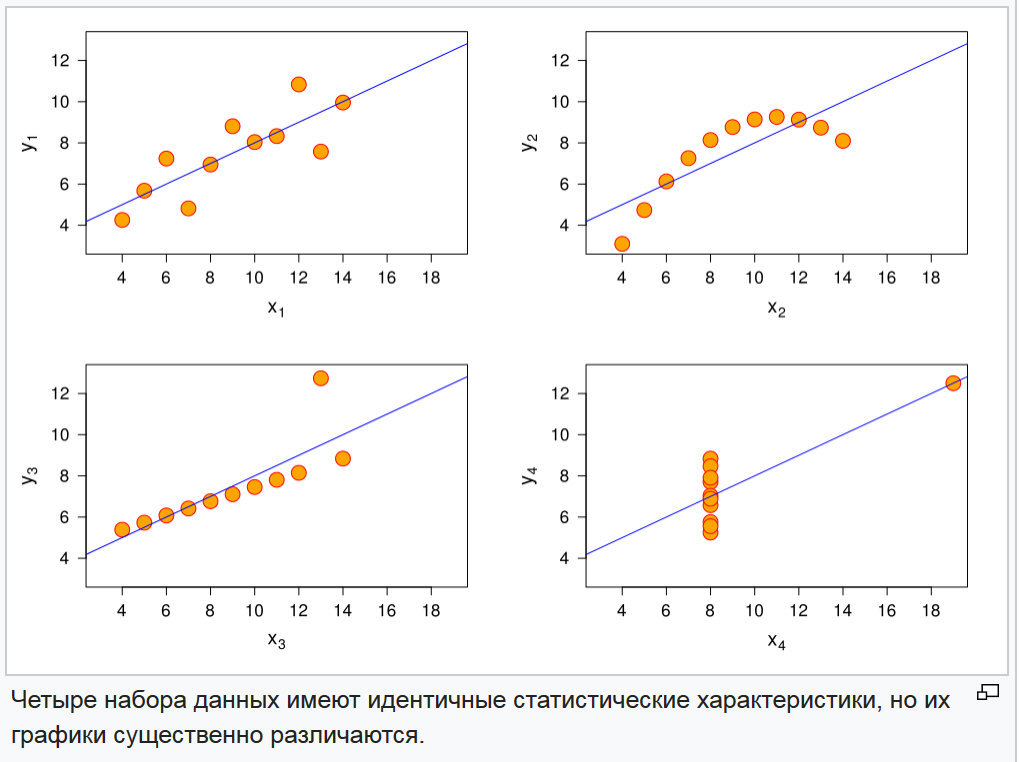Fig. 3. Gráficas de cuatro funciones aleatorias.

El problema de distinguir estas funciones se resuelve simplemente comparando los momentos de órdenes superiores y sus indicadores normalizados: coeficiente de asimetría y coeficiente de exceso . Estos indicadores se presentan en la Figura 4.


Fig. 4. Indicadores de momentos de tercer y cuarto orden y la asimetría y coeficientes en exceso de cuatro funciones aleatorias.

Como se puede ver en la tabla de la Figura 4, la combinación de estos indicadores para todas las funciones es diferente.
La primera conclusión, que naturalmente sugiere que la información sobre las posiciones relativas de los puntos se almacena en los parámetros de distribución a un nivel más alto que la varianza de la distribución aleatoria.

Muchos analistas están tratando de aislar ecuaciones de regresión particulares en grandes datos y, hasta ahora, este es un método para seleccionar la ecuación con la dispersión residual más pequeña. No había mucho que agregar. Pero llamé la atención sobre el hecho de que esta es toda la información, y la información tiene un indicador de entropía . Y, la entropía, tiene sus límites desde 0, cuando la información está completamente determinada al ruido blanco. Y el ruido blanco en el canal de transmisión tiene una distribución uniforme.

Cuando se requiere analizar los datos, inicialmente se supone que contienen datos relacionados que deben formalizarse como una relación. Y esto sugiere que los datos no son ruido blanco. Es decir, la primera etapa es la selección de la ecuación de regresión y la determinación de la varianza residual. Si la regresión se elige correctamente, entonces la varianza residual obedecerá la ley de distribución normal. Veamos y, en las Figuras 5-7, se presentan las fórmulas de entropía para una variable aleatoria distribuida uniformemente y distribuida normalmente.



Fig. 5. La fórmula de la entropía diferencial para una cantidad normalmente distribuida (VV Afanasyev. Teoría de la probabilidad en preguntas y tareas . Ministerio de Educación y Ciencia de la Federación de Rusia Universidad Pedagógica Estatal de Yaroslavl, en honor a K. D. Ushinsky)


Fig. 6. La fórmula de la entropía diferencial para una cantidad normalmente distribuida (Pugachev VS La teoría de las funciones aleatorias y su aplicación a los problemas de control automático . Ed. 2º, revisado y complementado. - M.: Fizmatlit, 1960. - 883 p.)


Fig. 7. La fórmula de la entropía diferencial para una cantidad uniformemente distribuida (Pugachev VS La teoría de las funciones aleatorias y su aplicación a los problemas de control automático . Ed. 2º, revisado y complementado. - M.: Fizmatlit, 1960. - 883 p.)

A continuación, mostramos un ejemplo. Pero primero tomamos las condiciones de que cada una de las cuatro funciones es la coordenada del hiperplano, es decir, al mismo tiempo verificamos el funcionamiento del modelo en el espacio multidimensional. Dibuja una convolución de un hipercubo en un plano. El mecanismo se presenta en la Figura 8.




Fig. 8. Datos iniciales con el mecanismo de convolución.


Fig. 9. Agrupación agregada en la figura.


Fig. 10. Parámetros de distribuciones de cuatro funciones aleatorias y una agrupación de resumen.

Considere el mecanismo para elegir el tamaño del intervalo de partición. Las condiciones iniciales se presentan en la Figura 11.


Fig. 11. Las condiciones iniciales para dividir en intervalos.

Condición 1. Debe tener una probabilidad distinta de cero en la región de variación, ya que de lo contrario, la entropía es igual al infinito. Tanto para la muestra inicial como para la residual.

Condición 2. Dado que es imposible ignorar la posibilidad de un valor atípico en los datos nuevos, etc., para los intervalos extremos, es necesario establecer la probabilidad de acuerdo con la ley teórica de distribución de probabilidad normal u otra generalmente aceptada, de acuerdo con el principio de la probabilidad de colas.

Condición 3. El paso del intervalo debe proporcionar el número mínimo requerido de intervalos en la dispersión de la muestra residual.

Condición 4. El número de intervalos debe ser impar.

Condición 5. El número de intervalos debe garantizar un acuerdo confiable con la ley teórica de distribución seleccionada para el estudio.


Fig. 12. El resto de la distribución.

Defina el mecanismo de selección de intervalo en la Figura 13.


Fig. 13. El algoritmo de selección de intervalo

El problema principal, en mi opinión, fue decidir si introducir intervalos de cola o no. Si para la dispersión residual parecía bastante natural, entonces para la serie principal, es bastante tensa.


Fig. 14. Los resultados del procesamiento de valores de datos para determinar la entropía de la información

Conclusiones ¿Dónde se puede aplicar esta herramienta?

Al comparar los indicadores resultantes de la tabla en la Figura 14, se puede ver que respondieron al cambio en la estructura de datos. Y esto significa que la herramienta tiene una sensibilidad y le permite resolver problemas similares a la tarea del cuarteto Enskomb.

Sin duda, estos problemas pueden resolverse con la ayuda de momentos de órdenes superiores. Pero, en esencia, la entropía informativa depende de la varianza de una variable aleatoria, es decir, es una característica de varianza de un tercero. Entonces, podemos indicar los intervalos donde el uso del análisis de varianza puede conducir a un resultado específico.

La característica numérica de la entropía permite realizar un análisis de correlación con variables independientes. Como un ejemplo de la manifestación de una posible conexión, lo siguiente: Supongamos que, durante el intervalo de a a b, el nivel de ruido de una serie de datos aumentó, comparando los valores de variables independientes, encontramos que la variable xn ingresó al rango de más de 5 unidades, después de esto variable, disminuyó por debajo de +5, el ruido disminuyó. Además, se puede hacer una verificación adicional y, si se confirma esta hipótesis, en estudios posteriores, prohibir que la variable xn se eleve por encima de +5. Como en este caso, los datos se vuelven inútiles.

Supongo que hay otras opciones para usar esta herramienta.

Como usar

En este aspecto, se examina el mecanismo natural del "promedio móvil", supongo que el tamaño de muestra obtenido por la fórmula de tamaño de muestra del análisis estadístico dará un volumen razonable del área de deslizamiento. Según el análisis actual, se concluyó que el tamaño de la muestra debe determinarse a partir de la proporción mínima que cae en la menor probabilidad. En nuestro ejemplo, para la varianza residual, la fracción mínima del intervalo empírico es 0.15909. Esto debe hacerse, porque si algún intervalo en el volumen de deslizamiento está vacío, entonces en este caso la cifra de ruido será escandalosa o la regla funcionará que el logaritmo de 0 es igual a menos infinito. Y con un tamaño de muestra correctamente seleccionado, los valores trascendentales de este indicador indicarán un cambio cardinal en la estructura de la información.