Varios de mis colegas se enfrentan al problema de que para calcular algún tipo de métrica, por ejemplo, la tasa de conversión, debe validar toda la base de datos. O necesita realizar un estudio detallado para cada cliente, donde hay millones de clientes. Este tipo de kerry puede funcionar durante bastante tiempo, incluso en repositorios especialmente diseñados. No es muy divertido esperar 5-15-40 minutos hasta que se considere una métrica simple para descubrir que necesita calcular otra cosa o agregar otra cosa.
Una solución a este problema es el muestreo: no estamos tratando de calcular nuestra métrica en toda la matriz de datos, sino que tomamos un subconjunto que representa representativamente las métricas que necesitamos. Esta muestra puede ser 1000 veces más pequeña que nuestra matriz de datos, pero es lo suficientemente buena como para mostrar los números que necesitamos.
En este artículo, decidí demostrar cómo los tamaños de muestra de muestreo afectan el error métrico final.
El problema
La pregunta clave es: ¿qué tan bien describe la muestra la "población"? Como tomamos una muestra de una matriz común, las métricas que recibimos resultan ser variables aleatorias. Diferentes muestras nos darán diferentes resultados métricos. Diferente, no significa ninguno. La teoría de la probabilidad nos dice que los valores métricos obtenidos por muestreo deben agruparse alrededor del valor métrico verdadero (realizado en toda la muestra) con un cierto nivel de error. Además, a menudo tenemos problemas en los que se puede prescindir de un nivel de error diferente. Una cosa es determinar si obtenemos una conversión del 50% o del 10%, y otra cosa es obtener un resultado con una precisión del 50.01% frente al 50.02%.
Es interesante que desde el punto de vista de la teoría, el coeficiente de conversión observado por nosotros en toda la muestra también sea una variable aleatoria, porque La tasa de conversión "teórica" solo puede calcularse en una muestra de tamaño infinito. Esto significa que incluso todas nuestras observaciones en la base de datos en realidad dan una estimación de conversión con su precisión, aunque nos parece que estos números calculados son absolutamente exactos. También lleva a la conclusión de que incluso si hoy la tasa de conversión difiere de ayer, esto no significa que algo ha cambiado, sino que solo significa que la muestra actual (todas las observaciones en la base de datos) es de la población general (todo posible observaciones para este día, que ocurrieron y no ocurrieron) dieron un resultado ligeramente diferente al de ayer. En cualquier caso, para cualquier producto o analista honesto, esta debería ser una hipótesis básica.
Digamos que tenemos 1,000,000 de registros en una base de datos de tipo 0/1, que nos dicen si se ha producido una conversión en un evento. Entonces, la tasa de conversión es simplemente la suma de 1 dividido por 1 millón.
Pregunta: si tomamos una muestra de tamaño N, ¿cuánto y con qué probabilidad la tasa de conversión diferirá de la calculada en toda la muestra?
Consideraciones teóricas
La tarea se reduce a calcular el intervalo de confianza del coeficiente de conversión para una muestra de un tamaño dado para una distribución binomial.
Desde la teoría, la desviación estándar para la distribución binomial es:
S = sqrt (p * (1 - p) / N)
Donde
p - tasa de conversión
N - Tamaño de muestra
S - desviación estándar
No consideraré el intervalo de confianza directo de la teoría. Hay un matan bastante complicado y confuso, que en última instancia relaciona la desviación estándar y la estimación final del intervalo de confianza.
Desarrollemos una "intuición" sobre la fórmula de desviación estándar:
- Cuanto mayor sea el tamaño de la muestra, menor será el error. En este caso, el error cae en la dependencia cuadrática inversa, es decir aumentar la muestra 4 veces aumenta la precisión solo 2 veces. Esto significa que en algún momento aumentar el tamaño de la muestra no dará ninguna ventaja particular, y también significa que se puede obtener una precisión bastante alta con una muestra bastante pequeña.

- El error depende del valor de la tasa de conversión. El error relativo (es decir, la razón del error al valor de la tasa de conversión) tiene una tendencia "vil" a ser mayor, menor es la tasa de conversión:
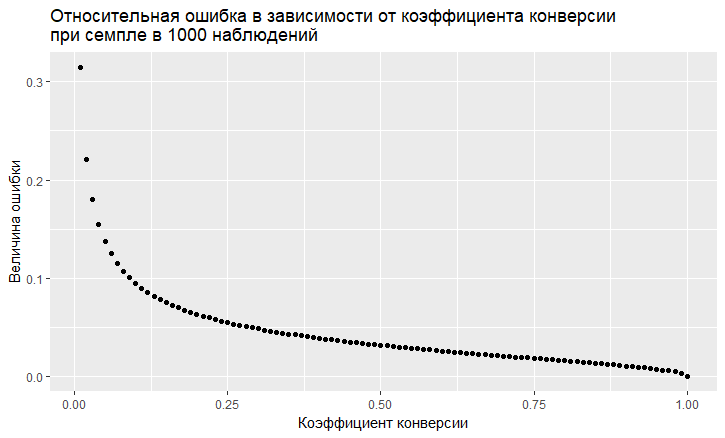
- Como vemos, el error "vuela" hacia el cielo con una tasa de conversión baja. Esto significa que si muestrea eventos raros, entonces necesita tamaños de muestra grandes, de lo contrario obtendrá una estimación de conversión con un error muy grande.
Modelado
Podemos alejarnos por completo de la solución teórica y resolver el problema "de frente". Gracias al lenguaje R, esto ahora es muy fácil de hacer. Para responder a la pregunta, ¿qué error obtenemos al muestrear? Puede hacer mil muestras y ver qué error obtenemos.
El enfoque es este:
- Tomamos diferentes tasas de conversión (de 0.01% a 50%).
- Tomamos 1000 muestras de 10, 100, 1000, 10000, 50,000, 100,000, 250,000, 500,000 elementos en la muestra
- Calculamos la tasa de conversión para cada grupo de muestras (1000 coeficientes)
- Construimos un histograma para cada grupo de muestras y determinamos en qué medida se encuentran el 60%, 80% y 90% de las tasas de conversión observadas.
Código R que genera datos:
sample.size <- c(10, 100, 1000, 10000, 50000, 100000, 250000, 500000) bootstrap = 1000 Error <- NULL len = 1000000 for (prob in c(0.0001, 0.001, 0.01, 0.1, 0.5)){ CRsub <- data.table(sample_size = 0, CR = 0) v1 = seq(1,len) v2 = rbinom(len, 1, prob) set = data.table(index = v1, conv = v2) print(paste('probability is: ', prob)) for (j in 1:length(sample.size)){ for(i in 1:bootstrap){ ss <- sample.size[j] subset <- set[round(runif(ss, min = 1, max = len),0),] CRsample <- sum(subset$conv)/dim(subset)[1] CRsub <- rbind(CRsub, data.table(sample_size = ss, CR = CRsample)) } print(paste('sample size is:', sample.size[j])) q <- quantile(CRsub[sample_size == ss, CR], probs = c(0.05,0.1, 0.2, 0.8, 0.9, 0.95)) Error <- rbind(Error, cbind(prob,ss,t(q))) }
Como resultado, obtenemos la siguiente tabla (habrá gráficos más adelante, pero los detalles se ven mejor en la tabla).
Veamos los casos con una conversión del 10% y con una conversión baja del 0.01%, porque Todas las características de trabajar con muestreo son claramente visibles en ellos.
Con una conversión del 10%, la imagen parece bastante simple:

Los puntos son los bordes del intervalo de confianza del 5-95%, es decir haciendo una muestra, en el 90% de los casos obtendremos CR en la muestra dentro de este intervalo. Escala vertical: tamaño de muestra (escala logarítmica), horizontal: valor de la tasa de conversión. La barra vertical es un "verdadero" CR.
Vemos lo mismo que vimos en el modelo teórico: la precisión aumenta a medida que crece el tamaño de la muestra, y uno converge bastante rápido y la muestra obtiene un resultado cercano a "verdadero". En total para 1000 muestras tenemos 8.6% - 11.7%, que será suficiente para varias tareas. Y en 10 mil ya 9.5% - 10.55%.
Las cosas son peores con eventos raros y esto es consistente con la teoría:

A una tasa de conversión baja de 0.01%, el problema está en las estadísticas de 1 millón de observaciones, y con las muestras la situación es aún peor. El error es simplemente gigantesco. En muestras de hasta 10.000, la métrica, en principio, no es válida. Por ejemplo, en una muestra de 10 observaciones, mi generador acaba de obtener 0 conversiones 1000 veces, por lo que solo hay 1 punto. Con 100 mil, tenemos una dispersión de 0.005% a 0.0016%, es decir, podemos hacer casi la mitad del coeficiente con tal muestreo.
También vale la pena señalar que cuando observa una conversión de una escala tan pequeña a 1 millón de pruebas, simplemente tiene un gran error natural. De esto se deduce que las conclusiones sobre la dinámica de tales eventos raros deben hacerse en muestras realmente grandes, de lo contrario, solo está persiguiendo fantasmas, fluctuaciones aleatorias en los datos.
Conclusiones:
- Muestreo de un método de trabajo para obtener estimaciones
- La precisión de la muestra aumenta al aumentar el tamaño de la muestra y disminuye al disminuir la tasa de conversión.
- La precisión de las estimaciones se puede modelar para su tarea y, por lo tanto, elegir el muestreo óptimo para usted.
- Es importante recordar que los eventos raros no se muestran bien
- En general, los eventos raros son difíciles de analizar; requieren grandes muestras de datos sin muestras.