Convierta la imagen en sonido, ¿qué puede escuchar?

Hola habr

Una publicación reciente aquí en el sitio describe un dispositivo que permite a las personas ciegas "ver" una imagen, transformándola usando ondas de sonido. Desde un punto de vista técnico, en ese artículo no había detalles en absoluto (y si la idea de un millón fuera robada ), pero el concepto en sí mismo parecía interesante. Teniendo algo de experiencia con el procesamiento de señales, decidí experimentar por mi cuenta.



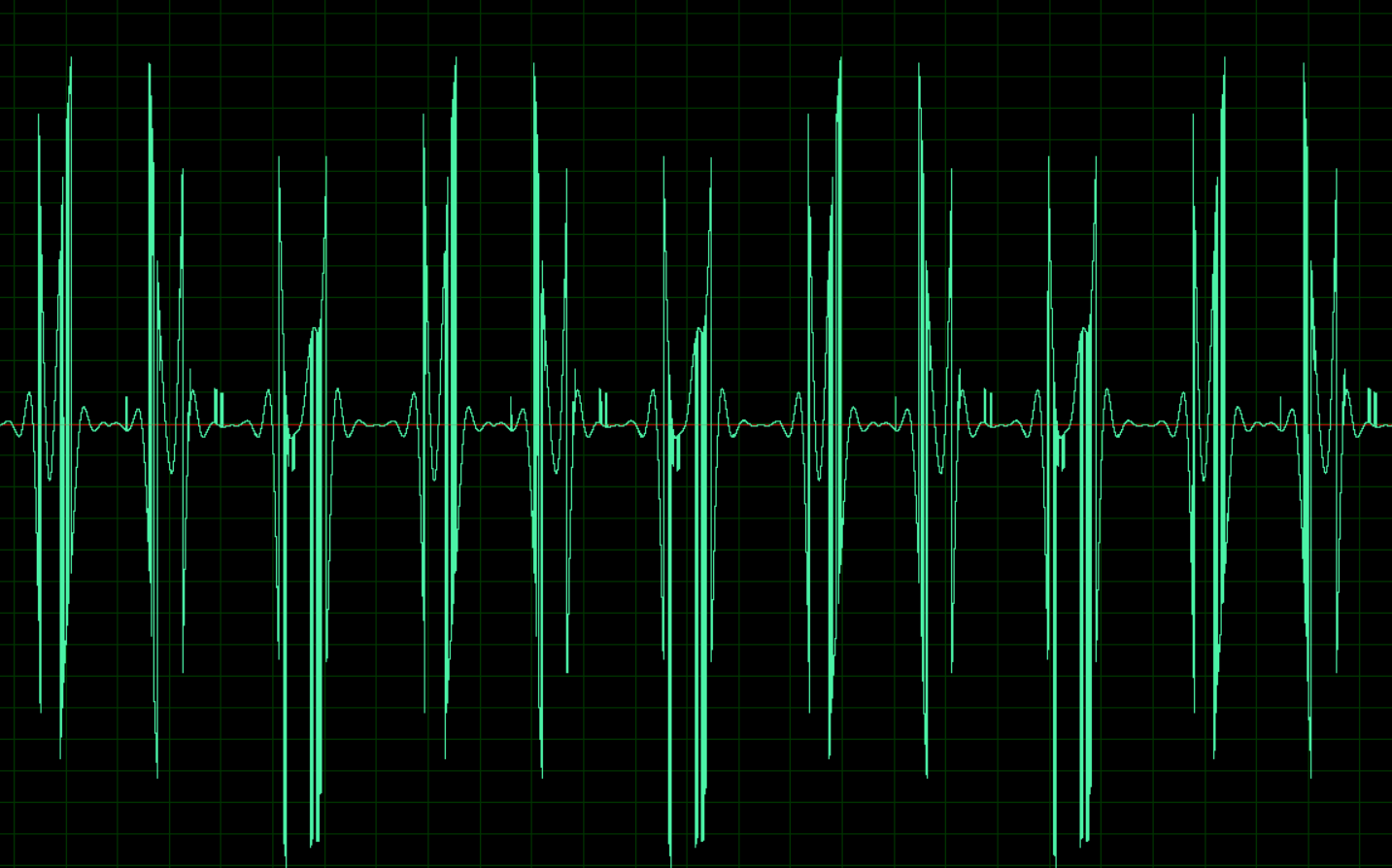
Lo que surgió, detalles y ejemplos de archivos debajo del gato.

Convierte 2D a 1D

La primera tarea obvia que nos espera es convertir una imagen "plana" bidimensional en una onda de sonido "unidimensional". Como se sugiere en los comentarios sobre ese artículo, es conveniente usar la curva de Hilbert para esto.

Básicamente se parece a un fractal, y la idea es que con un aumento en la resolución de la imagen, la posición relativa de los objetos no cambia (si el objeto estaba en la esquina superior izquierda de la imagen, entonces permanecerá allí ). Las diferentes dimensiones de las curvas de Hilbert nos pueden dar diferentes imágenes: 32x32 para N = 5, 64x64 para N = 6, y así sucesivamente. Al "caminar" por la imagen a lo largo de esta curva, obtenemos una línea, un objeto unidimensional.

La siguiente pregunta es el tamaño de la imagen. Intuitivamente quiero tomar una imagen más grande, pero hay un gran "pero": incluso la imagen es de 512x512, es de 262144 píxeles. Si convertimos cada punto en un pulso de audio, entonces a una frecuencia de muestreo de 44100, obtenemos una secuencia de hasta 6 segundos, y esto es demasiado largo: las imágenes deben actualizarse rápidamente, por ejemplo, usando una cámara web. No tiene sentido aumentar la frecuencia de muestreo; obtenemos frecuencias ultrasónicas inaudibles para el oído (aunque podría funcionar para un búho o un murciélago). Como resultado, se seleccionó una resolución de 128x128 por el método de búsqueda científica , que dará impulsos de 0.37c de longitud; por un lado, es lo suficientemente rápido como para navegar en tiempo real, por otro lado, es suficiente para detectar cualquier cambio en la forma de la señal por el oído.

Procesamiento de imagen

El primer paso es descargar la imagen, convertirla a b / n y escalarla al tamaño deseado. El tamaño de la imagen depende de la dimensión de la curva de Hilbert.

from PIL import Image from hilbertcurve.hilbertcurve import HilbertCurve import numpy as np from scipy.signal import butter, filtfilt # Create Hilbert curve dimension = 7 hilbert = HilbertCurve(dimension, n=2) print("Hilbert curve dimension:", dimension) # Maximum distance along curve print("Max_dist:", hilbert.max_h) # Maximum distance along curve print("Max_coord:", hilbert.max_x) # Maximum coordinate value in any dimension # Load PIL image f_name = "image01.png" img = Image.open(f_name) width, height = img.size out_size = hilbert_curve.max_x + 1 if width != out_size: img = img.resize((out_size, out_size), Image.ANTIALIAS) # Get image as grayscale numpy array img_grayscale = img.convert(mode='L') img_data = np.array(img_grayscale) 

El siguiente paso es formar una onda de sonido. Aquí, por supuesto, puede haber una gran cantidad de algoritmos y conocimientos, para la prueba que acabo de tomar el componente de brillo. Por supuesto, probablemente hay mejores formas.

 width, height = img_grayscale.size sound_data = np.zeros(width*height) for ii in range(width*height): coord_x, coord_y = hilbert_curve.coordinates_from_distance(ii) pixel_l = img_data[coord_x][coord_y] # Inverse colors (paper-like, white = 0, black = 255) pixel_l = 255 - pixel_l # Adjust values 0..255 to 0..8192 ampl = pixel_l*32 sound_data[ii] = ampl 

Desde el código, espero que todo esté claro. La función coordenadas_de_distancia hace todo el trabajo por nosotros al convertir las coordenadas (x, y) en una distancia en una curva de Hilbert, invertimos y convertimos el valor de brillo L en color.

Eso no es todo. Porque puede haber bloques grandes del mismo color en la imagen, esto puede dar lugar a la aparición de un "componente de CC" en el sonido: una larga serie de valores distintos de cero, por ejemplo [100,100,100, ...]. Para eliminarlos, aplicamos un filtro de paso alto (filtro de Butterworth ) a nuestra matriz con una frecuencia de corte de 50 Hz (la coincidencia con la frecuencia de la red es aleatoria). Hay una síntesis de filtros en la biblioteca scipy, que usaremos.

 def butter_highpass(cutoff, fs, order=5): nyq = 0.5 * fs normal_cutoff = cutoff / nyq b, a = butter(order, normal_cutoff, btype='high', analog=False) return b, a def butter_highpass_filter(data, cutoff, fs, order=5): b, a = butter_highpass(cutoff, fs, order) y = filtfilt(b, a, data) return y # Apply high pass filter to remove dc component cutoff_hz = 50 sample_rate = 44100 order = 5 wav_data = butter_highpass_filter(sound_data, cutoff_hz, sample_rate, order) 

El último paso es guardar la imagen. Porque la longitud de un pulso es corta, lo repetimos 10 veces, será más audible más cerca de una imagen real que se repite, por ejemplo, desde una cámara web.

 # Clip data to int16 range sound_output = np.clip(wav_data, -32000, 32000).astype(np.int16) # Save repeat = 10 sound_output_ntimes = np.tile(sound_output, repeat) wav_name = "ouput.wav" scipy.io.wavfile.write(wav_name, sample_rate, sound_output_ntimes) 

Resultados

El algoritmo anterior es, por supuesto, bastante primitivo. Quería verificar tres puntos: cuánto puede distinguir entre diferentes formas simples y cuánto puede estimar la distancia a las formas.

Prueba 1



La imagen corresponde a la siguiente señal de sonido:


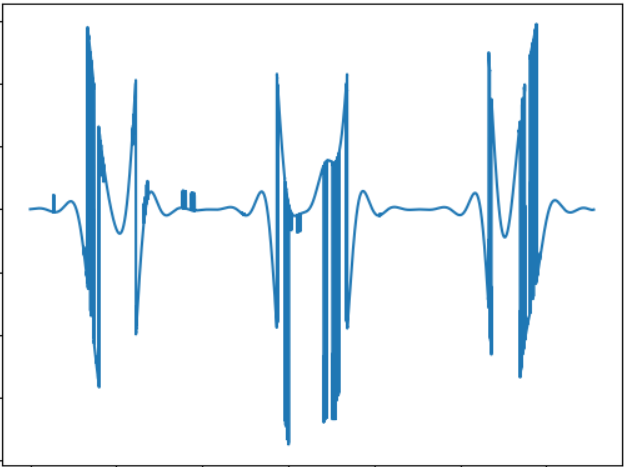
WAV: cloud.mail.ru/public/nt2R/2kwBvyRup

Prueba 2



La idea de esta prueba es comparar el "sonido" de un objeto de una forma diferente. Señal de sonido:


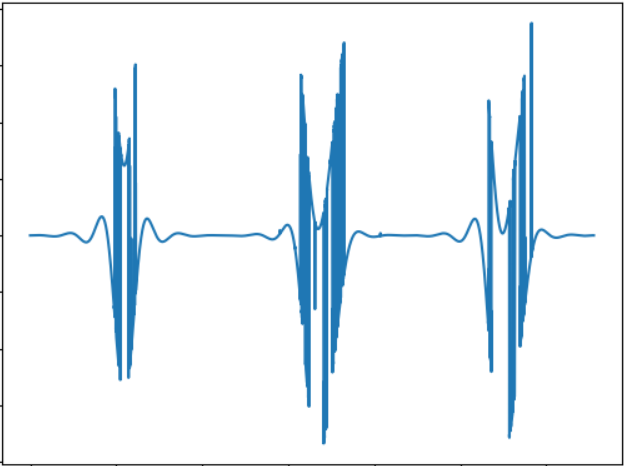
WAV: cloud.mail.ru/public/2rLu/4fCNRxCG2

Puede notar que el sonido es realmente diferente, y hay una diferencia de oído.

Prueba 3



La idea de la prueba es probar un objeto más pequeño. Señal de sonido:


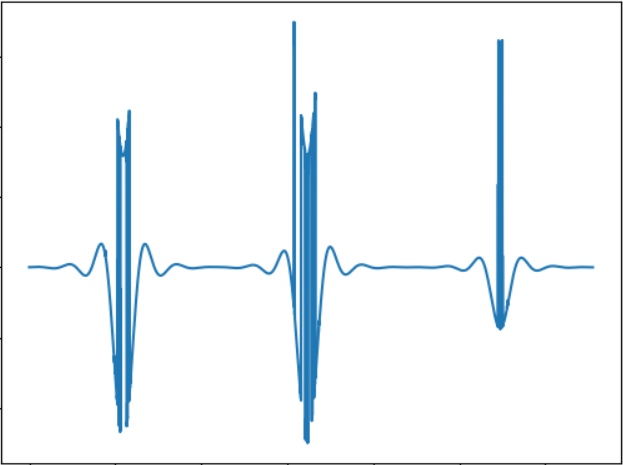
WAV: cloud.mail.ru/public/5GLV/2HoCHvoaY

En principio, cuanto menor sea el tamaño del objeto, menos habrá "ráfagas" en el sonido, por lo que la dependencia aquí es bastante directa.

Editar:

Como se sugiere en los comentarios, puede usar la transformación de Fourier para convertir directamente imágenes en sonido. Una prueba rápida realizada muestra los siguientes resultados (las imágenes son las mismas):
Prueba 1: cloud.mail.ru/public/2C5Z/5MEQ8Swjo
Prueba 2: cloud.mail.ru/public/2dxp/3sz8mjAib
Prueba 3: cloud.mail.ru/public/3NjJ/ZYrfdTYrk

Las pruebas suenan interesantes, al menos para cuadrados pequeños y grandes (archivos 1 y 3), la diferencia en la audición es notable. Pero la forma de las figuras (1 y 2) prácticamente no difiere, por lo que también hay algo en qué pensar. Pero en general, el sonido obtenido usando FFT, por oído, me gusta más.

Conclusión

Esta prueba, por supuesto, no es una disertación, sino simplemente una prueba de concepto, realizada en unas pocas horas de tiempo libre. Pero aun así, básicamente funciona, y es muy posible sentir la diferencia de oído. No sé si es posible aprender a navegar en el espacio con esos sonidos, hipotéticamente, probablemente después de algún entrenamiento. Aunque hay un campo enorme para mejoras y experimentos, por ejemplo, puede usar sonido estéreo, lo que le permitirá separar mejor los objetos de diferentes lados, puede experimentar con otros métodos para convertir imágenes en sonido, por ejemplo, codificar color a diferentes frecuencias, etc. Finalmente, es prometedor El uso de cámaras 3D capaces de percibir la profundidad (por desgracia, dicha cámara no está disponible). Por cierto, con la ayuda de un simple código OpenCV, el algoritmo anterior se puede adaptar para usar una cámara web, lo que le permitirá experimentar con imágenes dinámicas.

Bueno, como siempre, todos los experimentos exitosos.