🙆🏿 🐏 🙋🏿 Algoritmo criptográfico Grasshopper: casi el complejo ☠️ 🌳 💯

Este artículo detallará el algoritmo de cifrado de bloque definido en GOST R 34.12-2015 como Grasshopper. En qué se basa, cuál es la matemática de los algoritmos criptográficos de bloques y cómo se implementa este algoritmo en Java.

Quién, cómo, cuándo y por qué desarrolló este algoritmo permanecerá fuera del alcance del artículo, ya que en este caso tenemos poco interés, excepto:

Saltamontes = Kuznetsov, Nechaev Y Compañía.

Dado que la criptografía se basa principalmente en las matemáticas, de modo que una explicación adicional no cause muchas preguntas, primero debe analizar los conceptos básicos y las funciones matemáticas sobre las que se basa este algoritmo.

Campos Galois

La aritmética de los campos de Galois es aritmética polinómica, es decir, cada elemento de este campo es un polinomio. El resultado de cualquier operación también es un elemento de este campo. Un campo particular de Galois consiste en un rango fijo de números. La característica del campo se llama algún número primo p. Orden de campo, es decir la cantidad de sus elementos es un cierto grado natural de característica

$p ^ m$ , donde m ϵ N. Para m = 1, el campo se llama simple. En los casos en que m> 1, para la formación de un campo, también se requiere un polinomio generador de grado m; dicho campo se denomina extendido.

$Gf (p ^ m)$ - designación del campo de Galois. El polinomio generador es irreducible, es decir, simple (por analogía con los números primos es divisible por 1 y por sí mismo sin resto). Dado que trabajar con cualquier información es trabajar con bytes, y un byte es de 8 bits, tome como campo

$Gf (2 ^ 8)$ y el polinomio generador:

$x ^ 8 + x ^ 7 + x ^ 6 + x + 1.$

Sin embargo, para comenzar, analizaremos las operaciones básicas en un campo más simple

$Gf (2 ^ 3)$ con polinomio generador

$f (x) = x ^ 3 + x + 1$ .

Operación de adición

La más simple es la operación de suma, que en la aritmética de campo de Galois es un módulo de adición simple bit a bit 2 (RR).

Inmediatamente llamo la atención sobre el hecho de que el signo "+" aquí y en lo sucesivo se refiere al funcionamiento de XOR bit a bit, y no a la suma en la forma habitual.

La tabla de verdad de la función HOR

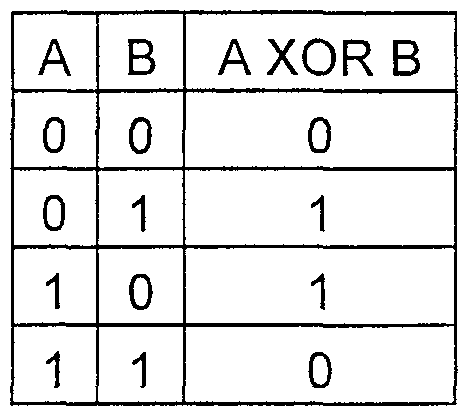
Un ejemplo:

$5 + 3 = 101 + 011 = 110_2 = 6_ {10}$

En forma polinómica, esta operación se verá como

$(x ^ 2 + 1) + (x + 1) = x ^ 2 + x = 110_2 = 6_ {10}$

Operación de multiplicación

Para llevar a cabo la operación de multiplicación, es necesario convertir los números en forma polinómica:

$5 = 101_2 = 1 * x ^ 2 + 0 * x ^ 1 + 1 * x ^ 0 = x ^ 2 + 1$

Como puede ver, el número en forma polinómica es un polinomio cuyos coeficientes son los valores de los dígitos en la representación binaria del número.

Multiplica dos números en forma polinómica:

$5 * 7 = (x ^ 2 + 1) * (x ^ 2 + x + 1) = x ^ 4 + x ^ 3 + x ^ 2 + x ^ 2 + x + 1 =$

$= x ^ 4 + x ^ 3 + x + 1 = 11011_2 = 27_ {10}$

El resultado de multiplicación 27 no está en el campo utilizado.

$Gf (2 ^ 3)$ (consiste en números del 0 al 7, como se mencionó anteriormente). Para combatir este problema, es necesario utilizar un polinomio generador.

También se supone que x satisface la ecuación

$f (x) = x ^ 3 + x + 1 = 0$ entonces

Hagamos una tabla de multiplicar:

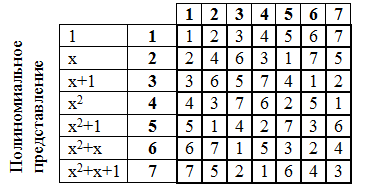
De gran importancia es la tabla de grados de los elementos del campo de Galois. La elevación a una potencia también se lleva a cabo en forma polinómica, similar a la multiplicación.

Un ejemplo:

$5 ^ 2 = (x ^ 2 + 1) ^ 2 = x ^ 4 + x ^ 2 + x ^ 2 + 1 = x ^ 4 + x ^ 2 + x + x ^ 2 + x + 1 =$

$= x (x ^ 3 + x + 1) + x ^ 2 + x + 1 = x ^ 2 + x + 1 = 111_2 = 7_ {10}$

Por lo tanto, compilamos una tabla de grados:

La tabla de grados es cíclica: el séptimo grado corresponde a cero, por lo que el octavo corresponde al primero, etc. Puede verificar esto si lo desea.

En los campos de Galois, existe el concepto de un término primitivo: un elemento de campo cuyos grados contienen todos los elementos de campo distintos de cero. Se puede ver que todos los elementos corresponden a esta condición (bueno, excepto 1, naturalmente). Sin embargo, este no es siempre el caso.

Para los campos que estamos considerando, es decir, con la característica 2, siempre elija 2. Como miembro primitivo, dada su propiedad, cualquier elemento del campo puede expresarse en términos del grado del miembro primitivo.

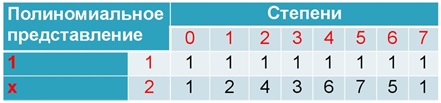
Un ejemplo:

$5 = 2 ^ 6.7 = 2 ^ 5$

Usando esta propiedad, y teniendo en cuenta la ciclicidad de la tabla de grados, intentaremos multiplicar los números nuevamente:

$5 * 7 = 2 ^ 6 * 2 ^ 5 = 2 ^ {(6 + 5)} = 2 ^ {(11mod7)} = 2 ^ 4 = 6$

El resultado coincidió con lo que calculamos anteriormente.

Ahora hagamos la división:

$6/5 = 2 ^ 4/2 ^ 6 = 2 ^ {(4-6)} = 2 ^ {((- 2) mod7)} = 2 ^ 5 = 7$

El resultado obtenido también es cierto.

Bueno, en aras de la exhaustividad, echemos un vistazo a elevar a un poder:

$5 ^ 2 = (2 ^ 6) ^ 2 = 2 ^ {(6 * 2)} = 2 ^ {(12mod7)} = 2 ^ 5 = 7$

Tal enfoque de multiplicación y división es mucho más simple que las operaciones reales que usan polinomios, y para ellos no hay necesidad de almacenar una tabla de multiplicación grande, sino solo una fila de grados de un miembro de campo primitivo.

Ahora de vuelta a nuestro campo

$Gf (2 ^ 8)$

El elemento cero del campo es uno, el primero es un dos, cada elemento posterior del segundo al 254 elemento se calcula como el anterior, multiplicado por 2, y si el elemento está fuera del campo, es decir, su valor es mayor que

$(2 ^ 8-1)$ entonces XOR se hace con el número

$195_ {10}$ , este número representa el polinomio irreducible del campo

$x ^ 8 + x ^ 7 + x ^ 6 + x + 1 = 2 ^ 8 + 2 ^ 7 ++ 2 ^ 6 + 2 + 1 = 451$ , traemos este número al campo

$451-256 = $ 19$ . Y el elemento 255 es nuevamente 1. Así que tenemos un campo que contiene 256 elementos, es decir, un conjunto completo de bytes, y hemos analizado las operaciones básicas que se realizan en este campo.

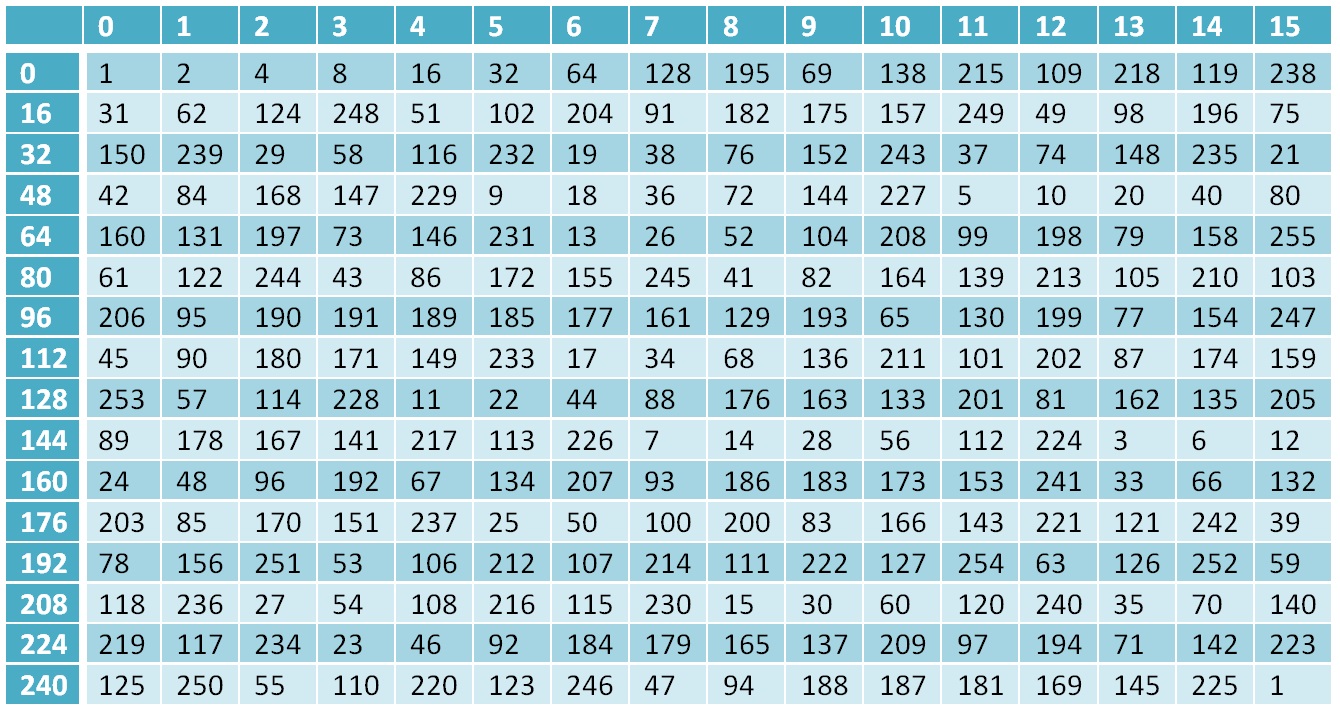
Tabla de poderes de dos para el campo

$Gf (2 ^ 8)$

Por qué era necesario: parte de los cálculos en el algoritmo Grasshopper se realiza en el campo de Galois, y los resultados de los cálculos, respectivamente, son elementos de este campo.

Red Feistel

Feistel Network es un método de encriptación en bloque desarrollado por Horst Feistel en IBM en 1971. Hoy la red de Feistel es la base de una gran cantidad de protocolos criptográficos.

La red Feistel opera con bloques de texto claro:

El bloque se divide en dos partes iguales: izquierda L y derecha R.
El subbloque izquierdo L es cambiado por la función f usando la tecla K: X = f (L, K). Como función, puede haber cualquier transformación.
El subbloque resultante X se agrega módulo 2 con el subbloque derecho R, que permanece sin cambios: X = X + R.
Las partes resultantes se intercambian y pegan.

Esta secuencia de acciones se llama célula Feistel.

Figura 1. Celda Feistel

La red Feistel consta de varias celdas. Los subbloques obtenidos en la salida de la primera celda van a la entrada de la segunda celda, los subbloques resultantes de la segunda celda van a la entrada de la tercera celda, y así sucesivamente.

Algoritmo de cifrado

Ahora nos hemos familiarizado con las operaciones utilizadas y podemos pasar al tema principal, a saber, el criptoalgoritmo de Grasshopper.

La base del algoritmo es la llamada red SP: red de sustitución-permutación. El cifrado basado en la red SP recibe un bloque y una clave en la entrada y realiza varias rondas alternas que consisten en etapas de sustitución y etapas de permutación. Grasshopper realiza nueve rondas completas, cada una de las cuales incluye tres operaciones consecutivas:

La operación de aplicar una clave redonda o XOR bit a bit de una clave y un bloque de datos de entrada;
Conversión no lineal, que es un simple reemplazo de un byte con otro de acuerdo con la tabla;
Transformación lineal. Cada byte del bloque se multiplica en el campo de Galois por uno de los coeficientes de la serie (148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1) dependiendo del ordinal Números de bytes (se presenta una serie para los números de serie del 15 al 0, como se muestra en la figura). Los bytes se suman módulo 2, y los 16 bytes del bloque se desplazan hacia el orden inferior, y el número resultante se escribe en lugar del byte leído.

La última décima ronda no está completa, incluye solo la primera operación XOR.

Grasshopper es un algoritmo de bloque, funciona con bloques de datos de 128 bits o 16 bytes de longitud. La longitud de la clave es de 256 bits (32 bytes).

Figura 2. El esquema de cifrado y descifrado del bloque de datos

El diagrama muestra la secuencia de operaciones, donde S es una transformación no lineal, L es una transformación lineal, Ki son teclas redondas. La pregunta surge de inmediato: ¿de dónde vienen las teclas redondas?

Formación de clave redonda

Las claves iterativas (o redondas) se obtienen mediante ciertas transformaciones basadas en una clave maestra, cuya longitud, como ya sabemos, es de 256 bits. Este proceso comienza dividiendo la clave maestra por la mitad, de modo que se obtiene el primer par de claves redondas. Se utilizan ocho iteraciones de la red Feistel para generar cada par de teclas redondas posteriores, se utiliza una constante en cada iteración, que se calcula aplicando una transformación lineal del algoritmo al valor del número de iteración.

El esquema para obtener claves iterativas (redondas)

Si recordamos la Figura 1, entonces el subbloque izquierdo L es la mitad izquierda de la clave original, el subbloque derecho R es la mitad derecha de la clave original, K es la constante Ci, la función f es la secuencia de operaciones R XOR Ci, transformación no lineal, transformación lineal.

Las constantes de iteración Ci se obtienen utilizando la transformación L del número de secuencia de iteración.

Entonces, para cifrar un bloque de texto, primero debemos calcular 32 constantes iterativas, luego calcular 10 teclas redondas basadas en la clave y luego realizar la secuencia de operaciones que se muestra en la Figura 2.

Comencemos calculando las constantes:
Primera const

$C_1 = 1_ {10} = 00000001_2 = 01_ {16}$ , sin embargo, todas las transformaciones en nuestro algoritmo se realizan con bloques de 16 bytes de largo, por lo tanto, es necesario complementar la constante con la longitud del bloque, es decir, agregar 15 bytes cero a la derecha, obtenemos

$C_1 = 01000000000000000000000000000000$

Multiplíquelo por una serie (1, 148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148) de la siguiente manera:

$a_ {15} = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$

$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 +$

$+ a_5 * 194 + a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$

(Esta igualdad se da en las operaciones de los campos de Galois)
Como todo, excepto el byte cero, es igual a 0, y el byte cero se multiplica por 1, obtenemos 1 y lo escribimos en el orden superior del número, desplazando todos los bytes al orden inferior, obtenemos:

$C_1 = 00000000000000000000000000000001$

Repite las mismas operaciones. Esta vez

$a_ {15} = 1$ , todos los demás bytes son 0, por lo tanto, solo queda el primero de los términos

$a_ {15} * 148 = 1 * 148 = 148_ {10} = 94_ {16}$ obtenemos:

$C_1 = 00000000000000000000000000000194$

Hacemos la tercera iteración, aquí hay dos términos distintos de cero:

$a_ {15} * 148 + a_ {14} * 32 = 148 * 148 + 1 * 32 =$

$= 10010100 * 10010100 + 00000001 * 00100000 =$

$= (x ^ 7 + x ^ 4 + x ^ 2) * (x ^ 7 + x ^ 4 + x ^ 2) + 1 * x ^ 5 = x ^ {14} + x ^ 8 + x ^ 4 + x ^ 5 =$

$= x ^ 6 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {13} + x ^ {12} + x ^ 7 + x ^ 6 + x ^ 8 + x ^ 4 + x ^ 5 =$

$= x ^ 5 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {11} + x ^ 5 + x ^ 7 + x ^ 8 + x ^ 4 + x ^ 5 =$

$= x ^ 3 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {10} + x ^ 9 + x ^ 3 + x ^ 8 + x ^ 7 =$

$= x ^ 2 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ 2 + x ^ 7 = x ^ 7 + x ^ 2 = 132_ {10}$

$132_ {10} = 84_ {16}$

Según la tabla de grados, podría resolverse mucho más fácilmente:

$148 * 148 + 1 * 32 = 2 ^ {45} * 2 ^ {45} + 2 ^ 5 = 2 ^ {90} + 2 ^ 5 = 164 + 32 = 132$

$C_1 = 00000000000000000000000000019484$

Además, todo es exactamente igual, solo 16 iteraciones por cada constante

$C_1 = 000000000000000000000000019484DD$

$C_1 = 0000000000000000000000019484DD10$

$C_1 = 00000000000000000000019484DD10BD$

$C_1 = 000000000000000000019484DD10BD27$

$C_1 = 0000000000000000019484DD10BD275D$

$C_1 = 00000000000000019484DD10BD275DB8$

$C_1 = 000000000000019484DD10BD275DB87A$

$C_1 = 0000000000019484DD10BD275DB87A48$

$C_1 = 00000000019484DD10BD275DB87A486C$

$C_1 = 000000019484DD10BD275DB87A486C72$

$C_1 = 0000019484DD10BD275DB87A486C727$

$C_1 = 00019484DD10BD275DB87A486C7276A2$

Y la constante final:

$C_1 = 019484DD10BD275DB87A486C7276A2E6$

Otras constantes:

$C_2 = 02EBCB7920B94EBAB3F490D8E4EC87DC$

$C_3 = 037F4FA4300469E70B8ED8B4969A25B2$

$C_4 = 041555F240B19CB7A52BE3730B1BCD7B$

$C_5 = 0581D12F500CBBEA1D51AB1F796D6F15$

$C_6 = 06FE9E8B6008D20D16DF73ABEFF74AA7$

$C_7 = 076A1A5670B5F550AEA53BC79D81E8C9$

$C_8 = 082AAA2780A1FBAD895605E6163659F6$

$C_9 = 09BE2EFA901CDCF0312C4D8A6440FB98$

$C_ {10} = 0AC1615EA018B5173AA2953EF2DADE2A$

$C_ {11} = 0B55E583B0A5924A82D8DD5280AC7C44$

$C_ {12} = 0C3FFFD5C010671A2C7DE6951D2D948D$

$C_ {13} = 0DAB7B08D0AD40479407AEF96F5B36E3$

$C_ {14} = 0ED434ACE0A929A09F89764DF9C11351$

$C_ {15} = 0F40B071F0140EFD27F33E218BB7B13F$

$C_ {16} = 1054974EC3813599D1AC0A0F2C6CB22F$

$C_ {17} = 11C01393D33C12C469D642635E1A1041$

$C_ {18} = 12BF5C37E3387B2362589AD7C88035F3$

$C_ {19} = 132BD8EAF3855C7EDA22D2BBBAF6979D$

$C_ {20} = 1441C2BC8330A92E7487E97C27777F54$

$C_ {21} = 15D54661938D8E73CCFDA1105501DD3A$

$C_ {22} = 16AA09C5A389E794C77379A4C39BF888$

$C_ {23} = 173E8D18B334C0C97F0931C8B1ED5AE6$

$C_ {24} = 187E3D694320CE3458FA0FE93A5AEBD9$

$C_ {25} = 19EAB9B4539DE969E0804785482C49B7$

$C_ {26} = 1A95F6106399808EEB0E9F31DEB66C05$

$C_ {27} = 1B0172CD7324A7D35374D75DACC0CE6B$

$C_ {28} = 1C6B689B03915283FDD1EC9A314126A2$

$C_ {29} = 1DFFEC46132C75DE45ABA4F6433784CC$

$C_ {30} = 1E80A3E223281C394E257C42D5ADA17E$

$C_ {31} = 1F14273F33953B64F65F342EA7DB0310$

$C_ {32} = 20A8ED9C45C16AF1619B141E58D8A75E$

Ahora calcularemos las claves redondas de acuerdo con el esquema presentado anteriormente, tome la clave de cifrado:

$K = 7766554433221100FFEEDDCCBBAA9988$

$EFCDAB89674523011032547698BADCFE$

Entonces

$K_1 = 7766554433221100FFEEDDCCBBAA9988$

$K_2 = EFCDAB89674523011032547698BADCFE$

$K_1$ será el subbloque izquierdo de la red Feistel, y

$K_2$ - bien
Hagamos la operación

$K_1 + C_1$
Primer byte

$K_1$ es igual a

$77_ {16} = 01110111_2$
Primer byte

$C_1$ es igual a

$01_ {16} = 00000001_2$

$01110111_2 + 00000001_2 = 01110110_2 = 76_ {16}$

los bytes restantes se convierten de la misma manera, como resultado

$X (K_1, C_1) = K_1 + C_1$ :

$X (K_1, C_1) = 76F2D199239F365D479495A0C9DC3BE6$

A continuación, realizamos una transformación no lineal.

$S (X (K_1, C_1))$ . Se realiza según la tabla:

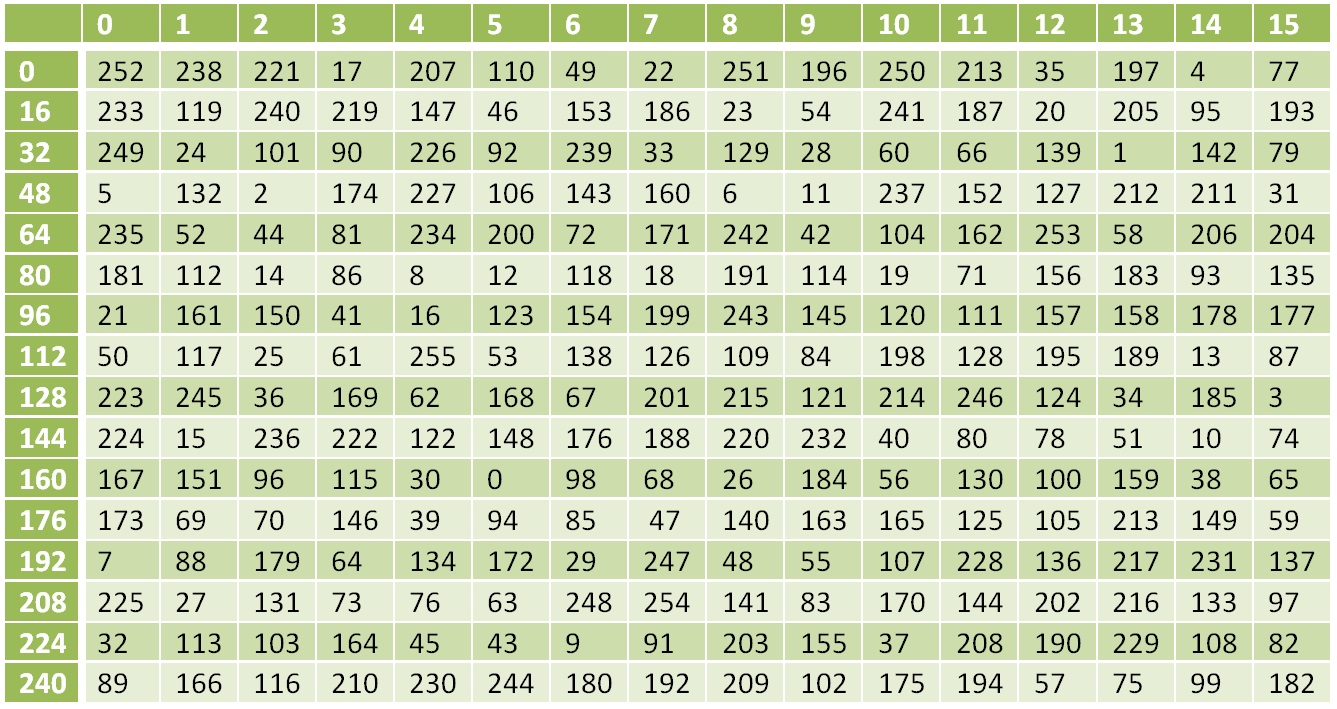Tabla de conversión no lineal

El número 0 se reemplaza por 252, 1 por 238, 17 por 119, etc.

$76_ {16} = 118_ {10}$

$S (118) = 138_ {10} = 8A_ {16}$

$S (X (K_1, C_1)) = 8A741BE85A4A8FB7AB7A94A737CA9809$

Ahora realiza una transformación lineal

$L (S (X (K_1, C_1)))$ , se consideró en detalle al calcular constantes iterativas, por lo que aquí solo damos el resultado final:

$L (S (X (K_1, C_1))) = A644615E1D0757926A5DB79D9940093D$

De acuerdo con el esquema de la celda Feistel, realizamos XOR con el subbloque derecho, es decir, con

$K_2$ :

$X (L (S (X (K_1, C_1))), K_2) = 4989CAD77A4274937A6FE3EB01FAD5C3$

Y el resultado obtenido a la salida de la primera celda Feistel:

$EFCDAB89674523011032547698BADCFE4989CAD77A4274937A6FE3EB01FAD5C3$

Este valor se reduce a la mitad y va a la entrada de la segunda celda Feistel, donde la segunda constante ya está en uso.

$C_2$ . Después de pasar por ocho celdas, obtenemos las siguientes 2 teclas

$K_3$ y

$K_4$ . Realizaremos ocho iteraciones de la red Feistel con ellos, obtendremos el siguiente par de claves, y así sucesivamente. Ocho iteraciones por par de claves, dado que inicialmente tenemos el primer par, luego se realizan 32 iteraciones en total, cada una con su propia constante.

Claves restantes:

$K_3 = 448CC78CEF6A8D2243436915534831DB$

$K_4 = 04FD9F0AC4ADEB1568ECCFE9D853453D$

$K_5 = ACF129F44692E5D3285E4AC468646457$

$K_6 = 1B58DA3428E832B532645C16359407BD$

$K_7 = B198005A26275770DE45877E7540E651$

$K_8 = 84F98622A2912AD73EDD9F7B0125795A$

$K_9 = 17E5B6CD732FF3A52331C77853E244BB$

$K_ {10} = 43404A8EA8BA5D755BF4BC1674DDE972$

Bloque de cifrado

Calculamos todas las claves y ahora finalmente podemos ir directamente a la encriptación del bloque de texto y si lee cuidadosamente todo lo escrito anteriormente, encriptar el texto no será difícil, ya que todas las operaciones utilizadas en este proceso y su secuencia han sido examinadas en detalle.

Tome el bloque de texto sin formato:

$T = 8899AABBCCDDEEFF0077665544332211$

ejecutar la secuencia de operaciones X, S, L

$X (T, K_1) = FFFFFFFFFFFFFFFFFFFF99BB99FF99BB99$

$S (X (T, K_1)) = B6B6B6B6B6B6B6B6B6E87DE8B6E87DE8$

$L (S (X (T, K_1))) = 30081449922F4ACFA1B055E386B697E2$

$T_1 = 30081449922F4ACFA1B055E386B697E2$

$X (T_1, K_2) = DFC5BFC0F56A69CEB18201951E0C4B1C$

$S (X (T_1, K_2)) = 61AC3B07F47891E74524EE945F23A214$

$L (S (X (T_1, K_2))) = 7290C6A158426FB396D562087A495E28$

$T_2 = 7290C6A158426FB396D562087A495E28$

y así sucesivamente, el resultado final se verá así:

$T_ {10} = CDEDD4B9428D465A3024BCBE909D677F$

Descifrado de bloque

Para descifrar el texto, debe usar las operaciones inversas en el orden inverso (consulte la Fig. 2).

La operación XOR es inversa a sí misma, la inversa de la operación S es la sustitución de acuerdo con la siguiente tabla:

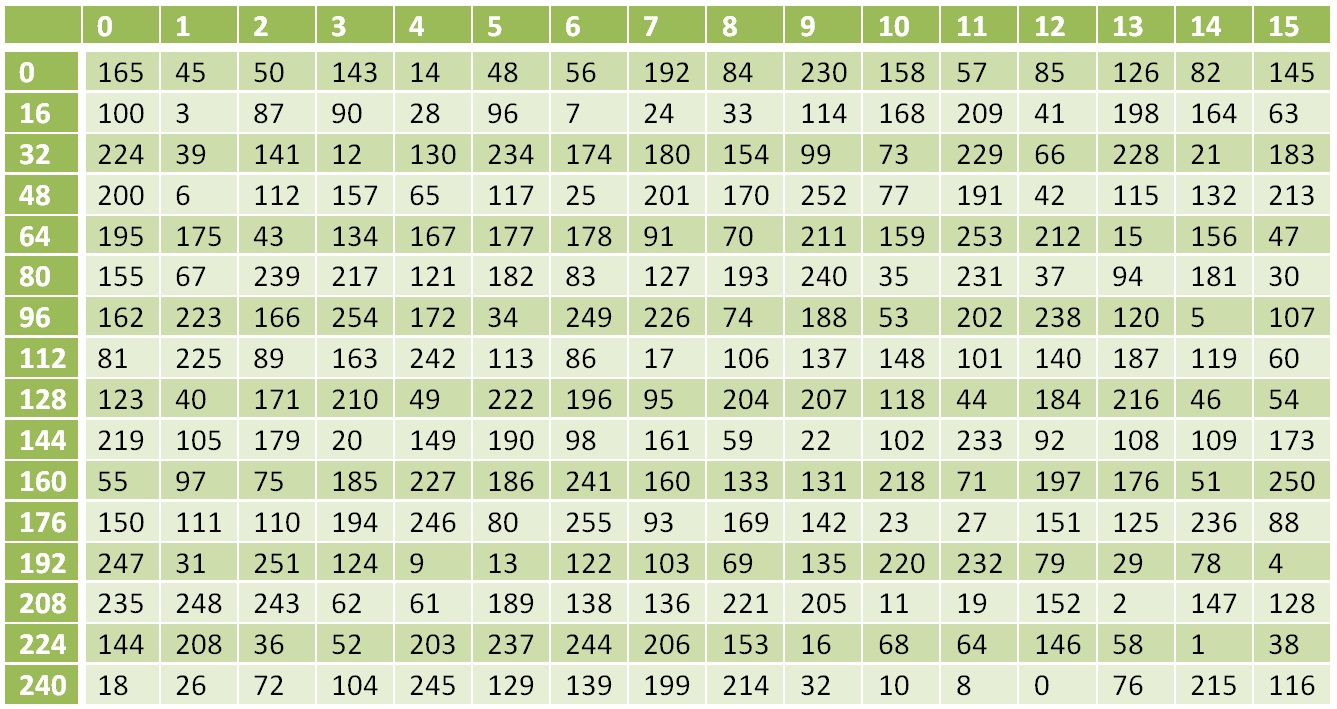Tabla de transformación no lineal inversa

La transformación inversa a la función L será:

$a_0 = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$

$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 + a_5 * 194 +$

$+ a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$

y un cambio en la dirección del nivel superior. (Repita la operación 16 veces)

Implementación de Java

Primero, definimos las constantes necesarias

static final int BLOCK_SIZE = 16; //   //     static final byte[] Pi = { (byte) 0xFC, (byte) 0xEE, (byte) 0xDD, 0x11, (byte) 0xCF, 0x6E, 0x31, 0x16, (byte) 0xFB, (byte) 0xC4, (byte) 0xFA, (byte) 0xDA, 0x23, (byte) 0xC5, 0x04, 0x4D, (byte) 0xE9, 0x77, (byte) 0xF0, (byte) 0xDB, (byte) 0x93, 0x2E, (byte) 0x99, (byte) 0xBA, 0x17, 0x36, (byte) 0xF1, (byte) 0xBB, 0x14, (byte) 0xCD, 0x5F, (byte) 0xC1, (byte) 0xF9, 0x18, 0x65, 0x5A, (byte) 0xE2, 0x5C, (byte) 0xEF, 0x21, (byte) 0x81, 0x1C, 0x3C, 0x42, (byte) 0x8B, 0x01, (byte) 0x8E, 0x4F, 0x05, (byte) 0x84, 0x02, (byte) 0xAE, (byte) 0xE3, 0x6A, (byte) 0x8F, (byte) 0xA0, 0x06, 0x0B, (byte) 0xED, (byte) 0x98, 0x7F, (byte) 0xD4, (byte) 0xD3, 0x1F, (byte) 0xEB, 0x34, 0x2C, 0x51, (byte) 0xEA, (byte) 0xC8, 0x48, (byte) 0xAB, (byte) 0xF2, 0x2A, 0x68, (byte) 0xA2, (byte) 0xFD, 0x3A, (byte) 0xCE, (byte) 0xCC, (byte) 0xB5, 0x70, 0x0E, 0x56, 0x08, 0x0C, 0x76, 0x12, (byte) 0xBF, 0x72, 0x13, 0x47, (byte) 0x9C, (byte) 0xB7, 0x5D, (byte) 0x87, 0x15, (byte) 0xA1, (byte) 0x96, 0x29, 0x10, 0x7B, (byte) 0x9A, (byte) 0xC7, (byte) 0xF3, (byte) 0x91, 0x78, 0x6F, (byte) 0x9D, (byte) 0x9E, (byte) 0xB2, (byte) 0xB1, 0x32, 0x75, 0x19, 0x3D, (byte) 0xFF, 0x35, (byte) 0x8A, 0x7E, 0x6D, 0x54, (byte) 0xC6, (byte) 0x80, (byte) 0xC3, (byte) 0xBD, 0x0D, 0x57, (byte) 0xDF, (byte) 0xF5, 0x24, (byte) 0xA9, 0x3E, (byte) 0xA8, (byte) 0x43, (byte) 0xC9, (byte) 0xD7, 0x79, (byte) 0xD6, (byte) 0xF6, 0x7C, 0x22, (byte) 0xB9, 0x03, (byte) 0xE0, 0x0F, (byte) 0xEC, (byte) 0xDE, 0x7A, (byte) 0x94, (byte) 0xB0, (byte) 0xBC, (byte) 0xDC, (byte) 0xE8, 0x28, 0x50, 0x4E, 0x33, 0x0A, 0x4A, (byte) 0xA7, (byte) 0x97, 0x60, 0x73, 0x1E, 0x00, 0x62, 0x44, 0x1A, (byte) 0xB8, 0x38, (byte) 0x82, 0x64, (byte) 0x9F, 0x26, 0x41, (byte) 0xAD, 0x45, 0x46, (byte) 0x92, 0x27, 0x5E, 0x55, 0x2F, (byte) 0x8C, (byte) 0xA3, (byte) 0xA5, 0x7D, 0x69, (byte) 0xD5, (byte) 0x95, 0x3B, 0x07, 0x58, (byte) 0xB3, 0x40, (byte) 0x86, (byte) 0xAC, 0x1D, (byte) 0xF7, 0x30, 0x37, 0x6B, (byte) 0xE4, (byte) 0x88, (byte) 0xD9, (byte) 0xE7, (byte) 0x89, (byte) 0xE1, 0x1B, (byte) 0x83, 0x49, 0x4C, 0x3F, (byte) 0xF8, (byte) 0xFE, (byte) 0x8D, 0x53, (byte) 0xAA, (byte) 0x90, (byte) 0xCA, (byte) 0xD8, (byte) 0x85, 0x61, 0x20, 0x71, 0x67, (byte) 0xA4, 0x2D, 0x2B, 0x09, 0x5B, (byte) 0xCB, (byte) 0x9B, 0x25, (byte) 0xD0, (byte) 0xBE, (byte) 0xE5, 0x6C, 0x52, 0x59, (byte) 0xA6, 0x74, (byte) 0xD2, (byte) 0xE6, (byte) 0xF4, (byte) 0xB4, (byte) 0xC0, (byte) 0xD1, 0x66, (byte) 0xAF, (byte) 0xC2, 0x39, 0x4B, 0x63, (byte) 0xB6 }; //     static final byte[] reverse_Pi = { (byte) 0xA5, 0x2D, 0x32, (byte) 0x8F, 0x0E, 0x30, 0x38, (byte) 0xC0, 0x54, (byte) 0xE6, (byte) 0x9E, 0x39, 0x55, 0x7E, 0x52, (byte) 0x91, 0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18, 0x21, 0x72, (byte) 0xA8, (byte) 0xD1, 0x29, (byte) 0xC6, (byte) 0xA4, 0x3F, (byte) 0xE0, 0x27, (byte) 0x8D, 0x0C, (byte) 0x82, (byte) 0xEA, (byte) 0xAE, (byte) 0xB4, (byte) 0x9A, 0x63, 0x49, (byte) 0xE5, 0x42, (byte) 0xE4, 0x15, (byte) 0xB7, (byte) 0xC8, 0x06, 0x70, (byte) 0x9D, 0x41, 0x75, 0x19, (byte) 0xC9, (byte) 0xAA, (byte) 0xFC, 0x4D, (byte) 0xBF, 0x2A, 0x73, (byte) 0x84, (byte) 0xD5, (byte) 0xC3, (byte) 0xAF, 0x2B, (byte) 0x86, (byte) 0xA7, (byte) 0xB1, (byte) 0xB2, 0x5B, 0x46, (byte) 0xD3, (byte) 0x9F, (byte) 0xFD, (byte) 0xD4, 0x0F, (byte) 0x9C, 0x2F, (byte) 0x9B, 0x43, (byte) 0xEF, (byte) 0xD9, 0x79, (byte) 0xB6, 0x53, 0x7F, (byte) 0xC1, (byte) 0xF0, 0x23, (byte) 0xE7, 0x25, 0x5E, (byte) 0xB5, 0x1E, (byte) 0xA2, (byte) 0xDF, (byte) 0xA6, (byte) 0xFE, (byte) 0xAC, 0x22, (byte) 0xF9, (byte) 0xE2, 0x4A, (byte) 0xBC, 0x35, (byte) 0xCA, (byte) 0xEE, 0x78, 0x05, 0x6B, 0x51, (byte) 0xE1, 0x59, (byte) 0xA3, (byte) 0xF2, 0x71, 0x56, 0x11, 0x6A, (byte) 0x89, (byte) 0x94, 0x65, (byte) 0x8C, (byte) 0xBB, 0x77, 0x3C, 0x7B, 0x28, (byte) 0xAB, (byte) 0xD2, 0x31, (byte) 0xDE, (byte) 0xC4, 0x5F, (byte) 0xCC, (byte) 0xCF, 0x76, 0x2C, (byte) 0xB8, (byte) 0xD8, 0x2E, 0x36, (byte) 0xDB, 0x69, (byte) 0xB3, 0x14, (byte) 0x95, (byte) 0xBE, 0x62, (byte) 0xA1, 0x3B, 0x16, 0x66, (byte) 0xE9, 0x5C, 0x6C, 0x6D, (byte) 0xAD, 0x37, 0x61, 0x4B, (byte) 0xB9, (byte) 0xE3, (byte) 0xBA, (byte) 0xF1, (byte) 0xA0, (byte) 0x85, (byte) 0x83, (byte) 0xDA, 0x47, (byte) 0xC5, (byte) 0xB0, 0x33, (byte) 0xFA, (byte) 0x96, 0x6F, 0x6E, (byte) 0xC2, (byte) 0xF6, 0x50, (byte) 0xFF, 0x5D, (byte) 0xA9, (byte) 0x8E, 0x17, 0x1B, (byte) 0x97, 0x7D, (byte) 0xEC, 0x58, (byte) 0xF7, 0x1F, (byte) 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67, 0x45, (byte) 0x87, (byte) 0xDC, (byte) 0xE8, 0x4F, 0x1D, 0x4E, 0x04, (byte) 0xEB, (byte) 0xF8, (byte) 0xF3, 0x3E, 0x3D, (byte) 0xBD, (byte) 0x8A, (byte) 0x88, (byte) 0xDD, (byte) 0xCD, 0x0B, 0x13, (byte) 0x98, 0x02, (byte) 0x93, (byte) 0x80, (byte) 0x90, (byte) 0xD0, 0x24, 0x34, (byte) 0xCB, (byte) 0xED, (byte) 0xF4, (byte) 0xCE, (byte) 0x99, 0x10, 0x44, 0x40, (byte) 0x92, 0x3A, 0x01, 0x26, 0x12, 0x1A, 0x48, 0x68, (byte) 0xF5, (byte) 0x81, (byte) 0x8B, (byte) 0xC7, (byte) 0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, (byte) 0xD7, 0x74 }; //    static final byte[] l_vec = { 1, (byte) 148, 32, (byte) 133, 16, (byte) 194, (byte) 192, 1, (byte) 251, 1, (byte) 192, (byte) 194, 16, (byte) 133, 32, (byte) 148 }; //     static byte[][] iter_C = new byte[32][16]; //     static byte[][] iter_key = new byte[10][64];

Vamos a crear todas las funciones principales:

 //  X static private byte[] GOST_Kuz_X(byte[] a, byte[] b) { int i; byte[] c = new byte[BLOCK_SIZE]; for (i = 0; i < BLOCK_SIZE; i++) c[i] = (byte) (a[i] ^ b[i]); return c; } //  S static private byte[] GOST_Kuz_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = Pi[data]; } return out_data; }

Para implementar la función L, necesitamos varias funciones auxiliares, una para calcular la multiplicación de números en el campo de Galois y otra para el cambio.

 //     static private byte GOST_Kuz_GF_mul(byte a, byte b) { byte c = 0; byte hi_bit; int i; for (i = 0; i < 8; i++) { if ((b & 1) == 1) c ^= a; hi_bit = (byte) (a & 0x80); a <<= 1; if (hi_bit < 0) a ^= 0xc3; // x^8+x^7+x^6+x+1 b >>= 1; } return c; } //  R     ,    L- static private byte[] GOST_Kuz_R(byte[] state) { int i; byte a_15 = 0; byte[] internal = new byte[16]; for (i = 15; i >= 0; i--) { if(i == 0) internal[15] = state[i]; else internal[i - 1] = state[i]; a_15 ^= GOST_Kuz_GF_mul(state[i], l_vec[i]); } internal[15] = a_15; return internal; } static private byte[] GOST_Kuz_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal = in_data; for (i = 0; i < 16; i++) { internal = GOST_Kuz_R(internal); } out_data = internal; return out_data; }

Funciones inversas:

 //  S^(-1) static private byte[] GOST_Kuz_reverse_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = reverse_Pi[data]; } return out_data; } static private byte[] GOST_Kuz_reverse_R(byte[] state) { int i; byte a_0; a_0 = state[15]; byte[] internal = new byte[16]; for (i = 1; i < 16; i++) { internal[i] = state[i - 1]; a_0 ^= GOST_Kuz_GF_mul(internal[i], l_vec[i]); } internal[0] = a_0; return internal; } static private byte[] GOST_Kuz_reverse_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal; internal = in_data; for (i = 0; i < 16; i++) internal = GOST_Kuz_reverse_R(internal); out_data = internal; return out_data; } //    static private void GOST_Kuz_Get_C() { int i; byte[][] iter_num = new byte[32][16]; for (i = 0; i < 32; i++) { for(int j = 0; j < BLOCK_SIZE; j++) iter_num[i][j] = 0; iter_num[i][0] = (byte) (i+1); } for (i = 0; i < 32; i++) { iter_C[i] = GOST_Kuz_L(iter_num[i]); } } // ,     static private byte[][] GOST_Kuz_F(byte[] in_key_1, byte[] in_key_2, byte[] iter_const) { byte[] internal; byte[] out_key_2 = in_key_1; internal = GOST_Kuz_X(in_key_1, iter_const); internal = GOST_Kuz_S(internal); internal = GOST_Kuz_L(internal); byte[] out_key_1 = GOST_Kuz_X(internal, in_key_2); byte key[][] = new byte[2][]; key[0] = out_key_1; key[1] = out_key_2; return key; } //     public void GOST_Kuz_Expand_Key(byte[] key_1, byte[] key_2) { int i; byte[][] iter12 = new byte[2][]; byte[][] iter34 = new byte[2][]; GOST_Kuz_Get_C(); iter_key[0] = key_1; iter_key[1] = key_2; iter12[0] = key_1; iter12[1] = key_2; for (i = 0; i < 4; i++) { iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[0 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[1 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[2 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[3 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[4 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[5 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[6 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[7 + 8 * i]); iter_key[2 * i + 2] = iter12[0]; iter_key[2 * i + 3] = iter12[1]; } } //    public byte[] GOST_Kuz_Encript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; for(i = 0; i < 9; i++) { out_blk = GOST_Kuz_X(iter_key[i], out_blk); out_blk = GOST_Kuz_S(out_blk); out_blk = GOST_Kuz_L(out_blk); } out_blk = GOST_Kuz_X(out_blk, iter_key[9]); return out_blk; } //   public byte[] GOST_Kuz_Decript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; out_blk = GOST_Kuz_X(out_blk, iter_key[9]); for(i = 8; i >= 0; i--) { out_blk = GOST_Kuz_reverse_L(out_blk); out_blk = GOST_Kuz_reverse_S(out_blk); out_blk = GOST_Kuz_X(iter_key[i], out_blk); } return out_blk; }

Bueno, y la función principal

 static byte[] key_1 = {0x77, 0x66, 0x55, 0x44, 0x33, 0x22, 0x11, 0x00, (byte) 0xff, (byte) 0xee, (byte) 0xdd, (byte) 0xcc, (byte) 0xbb, (byte) 0xaa, (byte) 0x99, (byte) 0x88}; static byte[] key_2 = {(byte) 0xef, (byte) 0xcd, (byte) 0xab, (byte) 0x89, 0x67, 0x45, 0x23, 0x01, 0x10, 0x32, 0x54, 0x76, (byte) 0x98, (byte) 0xba, (byte) 0xdc, (byte) 0xfe}; static byte[] blk = DatatypeConverter.parseHexBinary("8899aabbccddeeff0077665544332211"); public static void main(String[] args) { GOST_Kuz_Expand_Key(key_1, key_2); byte[] encriptBlok = GOST_Kuz_Encript(blk); System.out.println(DatatypeConverter.printHexBinary(encriptBlok)); byte[] decriptBlok = GOST_Kuz_Decript(encriptBlok); System.out.println(DatatypeConverter.printHexBinary(decriptBlok)); }

Aprendimos a cifrar un bloque de datos para cifrar texto cuya longitud es mayor que la longitud del bloque; hay varios modos descritos en el estándar - GOST 34.13-2015:

modo de reemplazo simple (Electronic Codebook, ECB);
modo gamma (contador, CTR);
modo gamma con retroalimentación de salida (Feedback de salida, OFB);
modo de engranaje de reemplazo simple (Cipher Block Chaining, CBC);
modo gamma con retroalimentación en texto cifrado (Cipher Feedback, CFB);
Modo de código de autenticación de mensaje (MAC).

En todos los modos, la longitud del texto siempre debe ser un múltiplo de la longitud del bloque, por lo que el texto siempre se rellena a la derecha con un solo bit y ceros a la longitud del bloque.

El modo más fácil es el modo de reemplazo simple. En este modo, el texto se divide en bloques, luego cada bloque se cifra por separado del resto, luego los bloques del texto cifrado se pegan y obtenemos un mensaje cifrado. Este modo es el más simple y el más vulnerable y casi nunca se aplica en la práctica.

Otros modos pueden considerarse en detalle más adelante.

Algoritmo criptográfico Grasshopper: casi el complejo