Estructura de datos del árbol B

Hola a todos! Lanzamos un nuevo conjunto para el curso "Algoritmos para desarrolladores" y hoy queremos compartir una traducción interesante preparada para los estudiantes de este curso.



En los árboles de búsqueda, como el árbol de búsqueda binario, el árbol AVL, el árbol rojo-negro, etc. cada nodo contiene solo un valor (clave) y un máximo de dos descendientes. Sin embargo, hay un tipo especial de árbol de búsqueda llamado B-tree (pronunciado Bi-tree). En él, el nodo contiene más de un valor (clave) y más de dos descendientes. El árbol B fue desarrollado en 1972 por Bayer y McCraith y se llamó Árbol de búsqueda de m-way de altura equilibrada . Su nombre moderno B-tree recibió más tarde.

Un árbol B se puede definir de la siguiente manera:
Un árbol B es un árbol de búsqueda equilibrado en el que cada nodo contiene muchas claves y tiene más de dos hijos.

Aquí, el número de claves en el nodo y el número de sus descendientes depende del orden del árbol B. Cada árbol B tiene un orden.

Un árbol B de orden m tiene las siguientes propiedades:

Propiedad 1: La profundidad de todas las hojas es la misma.
Propiedad 2: Todos los nodos, excepto la raíz, deben tener al menos (m / 2) - 1 claves y un máximo de m-1 claves.
Propiedad 3: todos los nodos sin hojas, excepto la raíz (es decir, todos los nodos internos), deben tener un mínimo de m / 2 descendientes.
Propiedad 4: si la raíz es un nodo sin hojas, debe tener al menos 2 descendientes.
Propiedad 5: Un nodo sin hojas con claves n-1 debe tener n hijos.
Propiedad 6: todas las claves en el nodo deben organizarse en orden ascendente de sus valores.

Por ejemplo, un árbol B de 4 órdenes contiene un máximo de 3 valores clave y un máximo de 4 elementos secundarios para cada nodo.


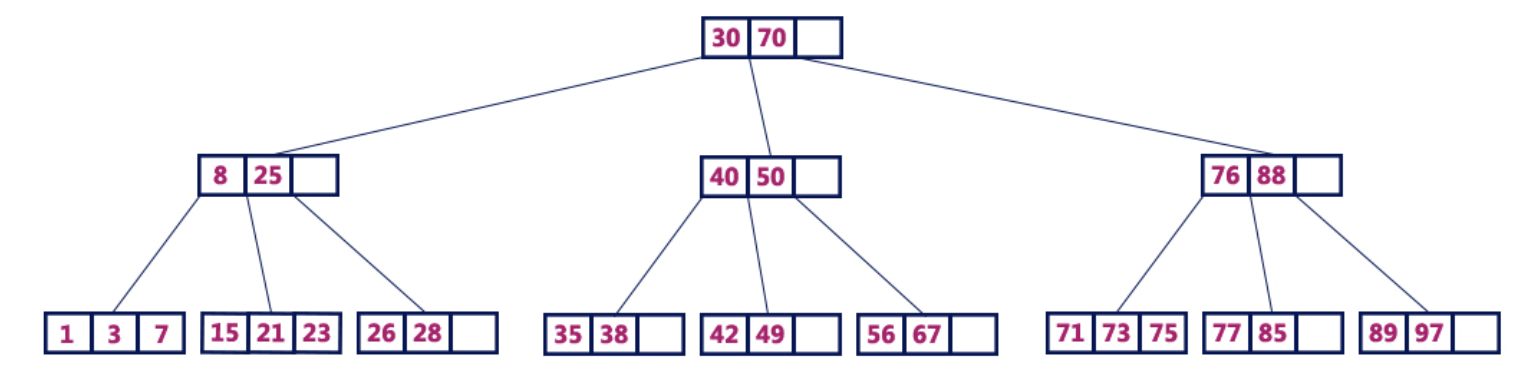B-tree 4 órdenes

Operaciones de árbol B

Las siguientes operaciones se pueden realizar en el árbol B:

1. Buscar
2. Insertar
3. Eliminar

Buscar árbol B

Las búsquedas de árbol B son similares a las búsquedas de árbol binario. En el árbol de búsqueda binario, la búsqueda comienza desde la raíz y cada vez que se toma una decisión bidireccional (ir a lo largo del subárbol izquierdo o derecho). En el árbol B, la búsqueda también comienza desde el nodo raíz, pero en cada paso se toma una decisión de n lados, donde n es el número total de descendientes del nodo en cuestión. En el árbol B, la complejidad de la búsqueda es O (log n) . La búsqueda es la siguiente:

Paso 1: lea el elemento para buscar.
Paso 2: Compare el elemento buscado con el primer valor clave en el nodo raíz del árbol.
Paso 3: si coinciden, imprima: "¡El nodo encontrado!" y completa la búsqueda.
Paso 4: si no coinciden, verifique que el valor del elemento sea más o menos que el valor de la clave actual.
Paso 5: Si el elemento que está buscando es más pequeño, continúe buscando el subárbol izquierdo.
Paso 6: si el elemento deseado es más grande, compare el elemento con el siguiente valor clave en el nodo y repita los pasos 3, 4, 5 y 6 hasta que se encuentre una coincidencia o hasta que el elemento buscado se compare con el último valor clave en el nodo hoja.
Paso 7: Si el último valor clave en el nodo de la lista no coincide con la búsqueda, imprima "¡Artículo no encontrado!" y completa la búsqueda.

Operación de inserción de árbol B

En el árbol B, un nuevo elemento solo se puede agregar a un nodo hoja. Esto significa que un nuevo par clave-valor siempre se agrega solo al nodo hoja. El inserto es el siguiente:

Paso 1: comprueba si el árbol está vacío.
Paso 2: si el árbol está vacío, cree un nuevo nodo con un nuevo valor clave y tómelo como el nodo raíz.
Paso 3: si el árbol no está vacío, busque un nodo hoja adecuado al que se agregará un nuevo valor utilizando la lógica del árbol de búsqueda binario.
Paso 4: Si hay una celda vacía en el nodo hoja actual, agregue un nuevo valor clave al nodo hoja actual, siguiendo el orden creciente de los valores clave dentro del nodo.
Paso 5: Si el nodo actual está lleno y no tiene celdas libres, divida el nodo hoja enviando el valor promedio al nodo padre. Repita el paso hasta que el valor a enviar se confirme en el nodo.
Paso 6: Si la separación ocurre con la raíz del árbol, entonces el promedio se convierte en la nueva raíz del árbol y la altura del árbol aumenta en uno.

Un ejemplo:

Creemos un árbol B de orden 3 agregando números del 1 al 10.

Insertar (1):
Como "1" es el primer elemento del árbol, se inserta en un nuevo nodo y este nodo se convierte en la raíz del árbol.



Insertar (2):
El elemento 2 se agrega a un nodo hoja existente. Ahora solo tenemos un nodo, por lo tanto, es la raíz y la hoja al mismo tiempo. Esta hoja tiene una celda vacía. Entonces "2" se mete en esta celda vacía.



Insertar (3):
El elemento 3 se agrega a un nodo hoja existente. Ahora solo tenemos un nodo, que es tanto la raíz como la hoja. Esta hoja no tiene una celda vacía. Por lo tanto, separamos este nodo enviando el valor promedio (2) al nodo padre. Sin embargo, el nodo actual no tiene un nodo padre. Por lo tanto, el valor promedio se convierte en el nodo raíz del árbol.



Insertar (4):
El elemento "4" es más grande que el nodo raíz con el valor "2", mientras que el nodo raíz no es una hoja. Por lo tanto, nos movemos a lo largo del subárbol derecho de "2". Llegamos al nodo hoja con el valor "3", que tiene una celda vacía. Por lo tanto, podemos insertar el elemento "4" en esta celda vacía.



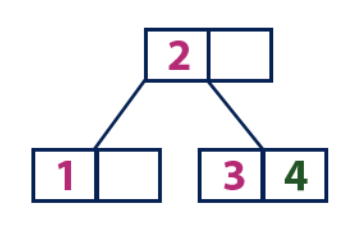Insertar (5):
El elemento "5" es más grande que el nodo raíz con el valor "2", mientras que el nodo raíz no es una hoja. Por lo tanto, nos movemos a lo largo del subárbol derecho de "2". Llegamos al nodo hoja y encontramos que ya está lleno y no tiene celdas vacías. Luego dividimos este nodo enviando el valor promedio (4) al nodo padre (2). El nodo padre tiene una celda vacía, por lo que el valor "4" se agrega al nodo en el que ya hay un valor de "2", y el nuevo elemento "5" se agrega como una nueva hoja.



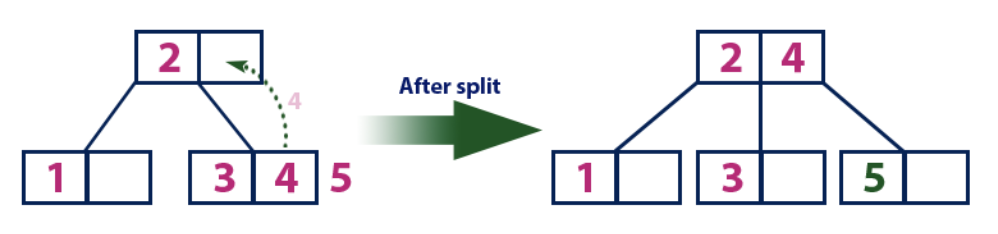Insertar (6):
El elemento "6" es más grande que los elementos de la raíz "2" y "4", que no es una hoja. Nos movemos a lo largo del subárbol derecho del elemento "4". Llegamos a una hoja con un valor de "5", que tiene una celda vacía, por lo que el elemento "6" se coloca justo en ella.



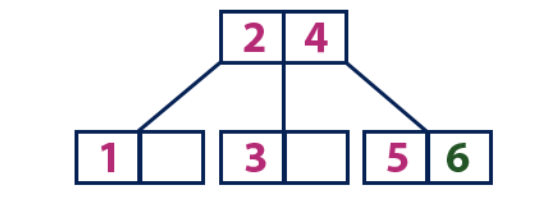Insertar (7):
El elemento "7" es más grande que los elementos de la raíz "2" y "4", que no es una hoja. Nos movemos a lo largo del subárbol derecho del elemento "4". Llegamos al nodo de la hoja y vemos que está lleno. Dividimos este nodo enviando el valor promedio de "6" hasta el nodo padre con los elementos "2" y "4". Sin embargo, el nodo padre también está lleno, por lo que dividimos el nodo con los elementos "2" y "4", enviando el valor "4" al nodo padre. Solo que este nodo aún no está allí. En este caso, el nodo con el elemento "4" se convierte en la nueva raíz del árbol.



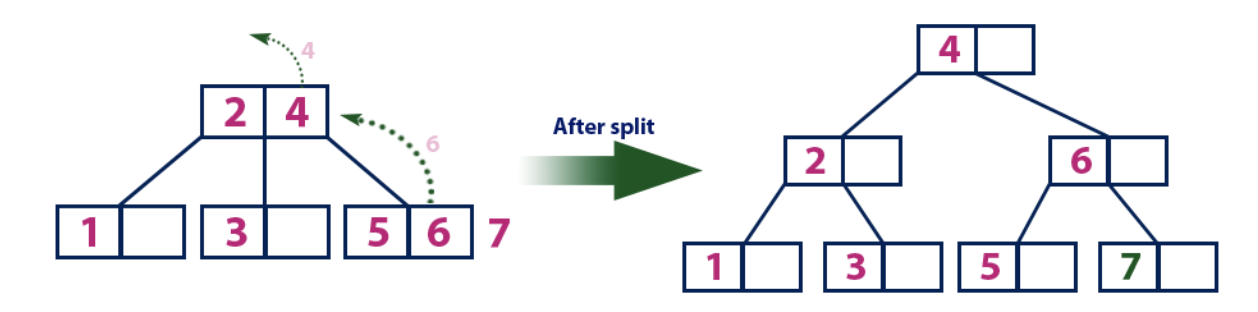Insertar (8):
El elemento 8 es más grande que el nodo raíz con un valor de 4, y el nodo raíz no es una hoja. Nos movemos a lo largo del subárbol derecho desde el elemento "4" y llegamos al nodo con el valor "6". "8" es mayor que "6" y el nodo con el elemento "6" no es una hoja, por lo que nos movemos a lo largo del subárbol derecho de "6". Llegamos al nodo hoja con "7", que tiene una celda vacía, por lo que ponemos "8".



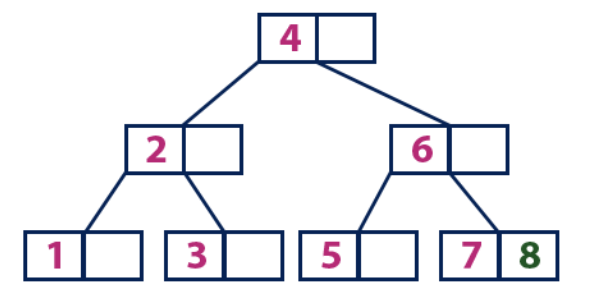Insertar (9):
El elemento 9 es más grande que el nodo raíz con un valor de 4, y el nodo raíz no es una hoja. Nos movemos a lo largo del subárbol derecho desde el elemento "4" y llegamos al nodo con el valor "6". "9" es mayor que "6" y el nodo con el elemento "6" no es una hoja, por lo que nos movemos a lo largo del subárbol derecho de "6". Llegamos al nodo hoja con los valores "7" y "8". El esta lleno. Dividimos este nodo enviando el valor promedio (8) al nodo padre. El nodo padre "6" tiene una celda vacía, por lo que ponemos "8". En este caso, se agrega un nuevo elemento "9" a la lista de nodos.



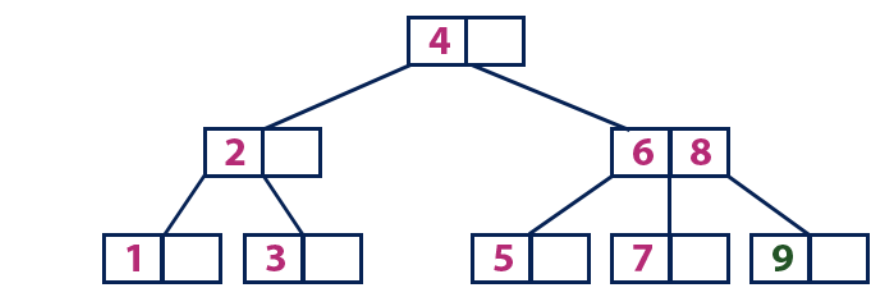
Insertar (10):
El elemento "10" es más grande que el nodo raíz con el valor "4", mientras que el nodo raíz no es una hoja. Nos movemos a lo largo del subárbol derecho desde el elemento "4" y llegamos al nodo con los valores "6" y "8". "10" es mayor que "6" y "8" y el nodo con estos elementos no es una hoja, por lo que nos movemos a lo largo del subárbol derecho de "8". Llegamos al nodo hoja con un valor de "9". Él tiene una celda vacía, así que ponemos "10" allí.



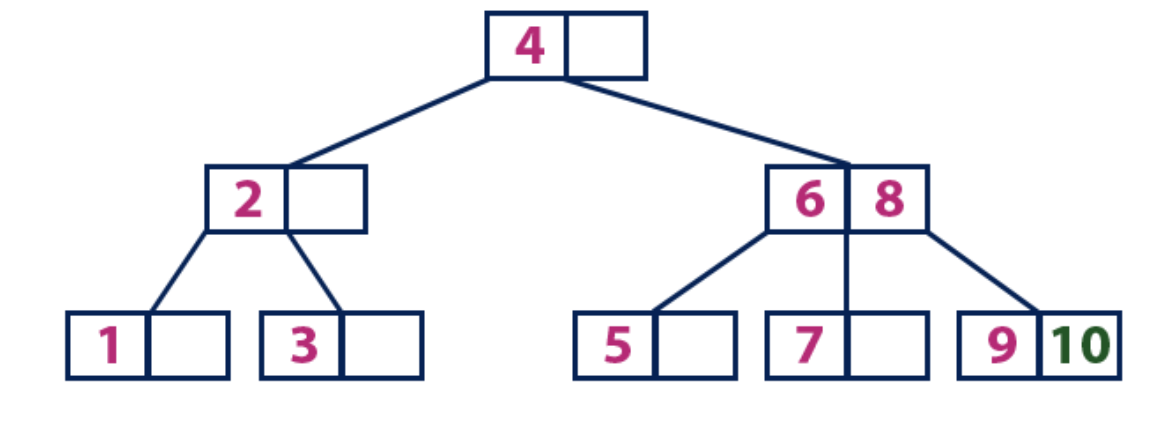
Sugerimos que comprenda independientemente en la práctica cómo se organizan los árboles B utilizando esta visualización .

Estamos esperando a todos en una lección abierta gratuita , que se llevará a cabo el 12 de julio. Hasta pronto!