De una función matemática mágica: una solución para gobernarlos a todos

Hace tres años, Marina Vyazovskaya, del Instituto Federal Suizo de Tecnología de Lausana, sorprendió a los matemáticos al descubrir la forma más densa de empaquetar esferas del mismo tamaño en espacios de ocho y 24 dimensiones (en el segundo caso, con la ayuda de cuatro coautores). Y ahora, ellos y sus coautores han demostrado algo aún más sorprendente: las configuraciones que resuelven el problema de empacar esferas densamente en las dimensiones mencionadas también resuelven un número infinito de otros problemas relacionados con la mejor disposición de puntos que intentan evitarse mutuamente.

Los puntos, por ejemplo, pueden denotar un conjunto infinito de electrones que se repelen entre sí y tratan de establecerse en la configuración con la energía más baja. O bien, estos puntos pueden indicar los centros de polímeros largos y retorcidos en solución, tratando de organizarse para no chocar con los vecinos. Hay muchas opciones para tales problemas, y no es obvio que cada uno tenga la misma solución. Los matemáticos creen que en la mayoría de las dimensiones es muy poco probable que sea así.

Pero los espacios, que constan de 8 y 24 dimensiones, contienen una configuración especial, muy simétrica de puntos, que, como sabemos ahora, resuelve simultáneamente todos estos problemas diferentes. En el lenguaje de las matemáticas, estas dos configuraciones se denominan "universalmente óptimas".

Este nuevo descubrimiento a gran escala resume seriamente el trabajo previo de Vyazovskaya y sus colegas. "Los fuegos artificiales no se detuvieron", dijo Thomas Hales , matemático de la Universidad de Pittsburgh, quien demostró en 1998 que el conocido arreglo piramidal de naranjas es la forma más densa de empacar esferas en un espacio tridimensional.

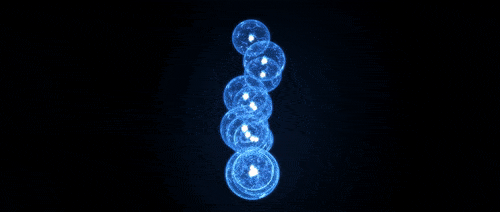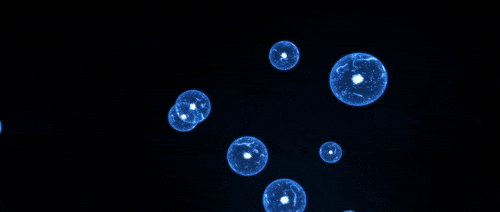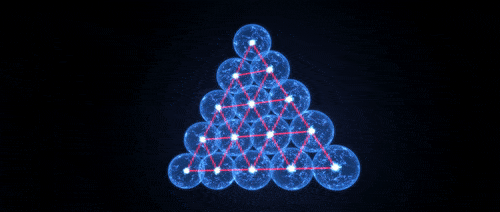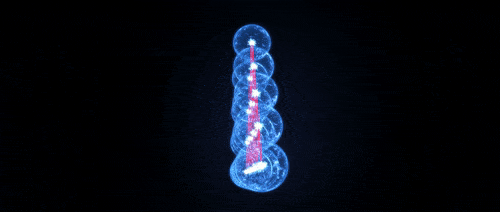
Ocho y 24 unen una dimensión en una pequeña lista de dimensiones que contienen configuraciones universalmente óptimas. En el plano bidimensional hay un candidato para la optimización universal, una cuadrícula de triángulos equiláteros, pero no hay pruebas. En un mundo tridimensional, reina un zoológico completo: diferentes configuraciones de puntos muestran diferentes resultados en diferentes circunstancias, y para algunas tareas los matemáticos ni siquiera tienen conjeturas tolerables sobre la mejor configuración.

"Cambia la medida, o cambia un poco la tarea, y la situación se vuelve incomprensible", dijo Richard Schwartz , matemático de la Universidad de Brown en Providence. "No sé por qué el universo matemático está tan organizado".

Probar la optimización universal es mucho más difícil que resolver el problema de las esferas de embalaje. En particular, porque la optimización universal incluye un número infinito de tareas diferentes a la vez, pero también porque estas tareas son más complicadas en sí mismas. En el empaque de las esferas, cada esfera se ocupa solo de sus vecinos más cercanos, pero en un problema como la distribución de electrones, cada uno de los electrones interactúa con todos los demás, independientemente de la distancia entre ellos. "Incluso a la luz de mis primeros trabajos, no esperaba que esta prueba universalmente óptima pudiera hacerse", dijo Hales.

"Es muy, muy impresionante", dijo Sylvia Serfati , matemática de la Universidad de Nueva York. "Esto está a la par con los principales avances matemáticos del siglo XIX".

Certificado mágico

Puede parecer extraño que las dimensiones 8 y 24 se comporten de manera diferente a, digamos, las dimensiones 7, 18 o 25. Pero los matemáticos saben desde hace mucho tiempo que el denso embalaje de objetos en el espacio funciona de manera diferente en diferentes dimensiones. Por ejemplo, considere una esfera multidimensional, definida simplemente como un conjunto de puntos ubicados a una distancia fija del centro. Si comparamos el volumen de la esfera con el volumen del cubo más pequeño que lo describe, entonces cuanto mayor sea la dimensión, menor será el cubo que ocupa la esfera. Si quisieras enviar un balón de fútbol de ocho dimensiones en la caja más pequeña posible, la pelota ocuparía menos del 2% del volumen de la caja, y todo lo demás sería un espacio vacío perdido.

En cada dimensión mayor que tres, es posible crear una configuración similar a la pirámide de naranjas, y al aumentar las dimensiones, crecen los espacios entre las esferas. Habiendo alcanzado la octava dimensión, de repente nos encontramos con el hecho de que en estos espacios hay suficiente espacio para exprimir las esferas allí. El resultado es una configuración extremadamente simétrica llamada rejilla E ₈ . En la 24ª dimensión, una red Lich surge de manera similar, cuando esferas adicionales se pueden apiñar en los huecos, creando así otra construcción bien conocida para el empaque de esferas.

Por razones que los matemáticos no comprenden completamente, estas dos redes aparecen repentinamente en un área de las matemáticas o en otra, desde la teoría de números y el análisis matemático hasta la física matemática. "No sé una razón para todo esto", dijo Henry Cohn del Microsoft Research New England Institute en Cambridge, Massachusetts, uno de los cinco autores del trabajo.

Durante más de diez años, los matemáticos han tenido pruebas numéricas convincentes de que E ₈ y la red Lich son universalmente óptimas en sus dimensiones, pero hasta hace poco no tenían idea de cómo demostrarlo. Luego, en 2016, Vyazovskaya dio el primer paso hacia esto, demostrando que estas dos redes son las mejores formas de empacar esferas.

Y si la prueba de Hales para el caso tridimensional se extiende a lo largo de cientos de páginas y requiere cálculos caros en la computadora, la prueba de Vyazovskaya para el caso de E ₈ cabe en 23 páginas. La esencia de sus argumentos está relacionada con la definición de una función "mágica" (como la llaman ahora los matemáticos), que da lo que Hales llamó un "certificado" para E ₈ para el mejor empaque de esferas: esta prueba es difícil de obtener, pero después de su aparición tiene una conveniencia instantánea. Por ejemplo, si alguien le pregunta si hay un número real x tal que el polinomio x ² - 6x + 9 se vuelve negativo, podría pensar en la respuesta. Sin embargo, al darse cuenta de que este polinomio es equivalente a (x - 3) ² , comprenderá de inmediato que la respuesta es "no", porque el cuadrado de un número real no puede ser negativo.

El método de búsqueda de la función mágica de Vyazovskaya demostró ser poderoso, y casi demasiado poderoso. La tarea de empaquetar esferas se refiere solo a la interacción de puntos cercanos, pero el enfoque Vyazovskaya parecía funcionar para interacciones de largo alcance, como es el caso de los electrones remotos.

Incertidumbre en las dimensiones superiores.

Para mostrar que la configuración de puntos en el espacio es universalmente óptima, primero es necesario determinar esta universalidad. No hay una configuración de puntos que sea óptima para ningún propósito: por ejemplo, cuando la fuerza de atracción actúa sobre los puntos, la configuración con la energía más baja no es una red, sino un montón masivo en el que todos los puntos están en un solo lugar.

Vyazovskaya, Cohn y sus colegas limitaron el alcance de su estudio a la universalidad de las fuerzas repulsivas. Más específicamente, consideraron fuerzas monótonas, es decir, aquellas en las que la repulsión se vuelve más fuerte cuando los puntos se acercan entre sí. Esta vasta familia incluye muchas de las fuerzas comunes del mundo físico. Esto incluye las leyes de poder del Universo, incluida la ley de Coulomb para partículas cargadas eléctricamente y las funciones gráficas gaussianas basadas en campanas que describen el comportamiento de entidades con muchas partes repulsivas independientes, como los polímeros largos. La tarea de empaquetar las esferas está en el borde exterior de este universo: el requisito de que las esferas no se crucen se convierte en repulsión infinitamente fuerte cuando la distancia entre sus centros es menor que su diámetro.

Para cualquiera de estas fuerzas monótonas, surge la pregunta: ¿cuál será la configuración con la energía más baja, el "estado fundamental", para un conjunto infinito de partículas? En 2006, Kon y Kumar desarrollaron un método para encontrar un límite de energía más pequeño del estado fundamental al comparar una función que describe la energía con funciones "auxiliares" más pequeñas con propiedades muy convenientes. Encontraron un suministro infinito de funciones auxiliares para cada dimensión, pero no sabían cómo encontrar la mejor función auxiliar.


Cinco autores del nuevo trabajo: Henry Cohn, Abkhinav Kumar, Marina Vyazovskaya, Stephen Miller y Danilo Radchenko

En la mayoría de las mediciones, las limitaciones numéricas descubiertas por Kohn y Kumar no se parecen a la energía de la mejor configuración posible. Pero en las dimensiones 8 y 24, los límites se acercaron asombrosamente a la energía E ₈ y la red Lich para cada fuerza repulsiva en la que Kon y Kumar probaron su método. Era natural pensar si, para cualquier fuerza repulsiva, existe alguna función auxiliar ideal que otorgue un límite que coincida exactamente con la energía E ₈ o la red Lich. Para la tarea de empaquetar esferas, esto fue exactamente lo que Vyazovskaya hizo hace tres años: descubrió una función auxiliar ideal, "mágica", al estudiar una clase de funciones llamadas funciones modulares , cuyas propiedades especiales de simetría hace siglos los convirtió en un objeto de estudio.

Cuando se trataba de otros problemas con puntos repulsivos, por ejemplo, el problema con los electrones, los investigadores sabían qué propiedades debería satisfacer cualquier función mágica: en ciertos puntos, debería tomar valores especiales, y su transformada de Fourier , que mide las frecuencias naturales de la función, debería tomar valores especiales en otros puntos. Lo que no sabían era si existía tal función.

Por lo general, es bastante simple construir una función que haga lo que necesita en sus puntos favoritos, pero es sorprendentemente difícil controlar tanto la función como su imagen de Fourier al mismo tiempo. "Cuando comienzas a hacer que algo haga uno de ellos, el otro hace algo completamente diferente de tus deseos", dijo Cohn.

De hecho, este meticuloso no es más que un principio encubierto de incertidumbre en física. El principio de incertidumbre de Heisenberg es que dice que cuanto más sepa sobre la ubicación de una partícula, menos sabrá sobre su momento, y viceversa, es un caso especial de este principio general, porque la onda de momento de la partícula es la transformada de Fourier de su onda de ubicación.

En el caso de la fuerza repulsiva en las dimensiones 8 o 24, Vyazovskaya presentó una hipótesis audaz: las restricciones que el equipo quería imponer a su función mágica y su imagen de Fourier están exactamente en el límite entre lo posible y lo imposible. Sospechaba que si agregaba más restricciones, no habría tal función; Si reduce las restricciones, puede haber muchas de esas funciones. Ella sugirió que en la situación que interesaba al equipo, debería haber exactamente una función adecuada.

"Creo que esta es una de las mejores características de Marina", dijo Cohn. "Ella es muy perspicaz y también muy valiente".

En ese momento, Kon era escéptico (la corazonada de Vyazovskaya parecía demasiado buena para ser verdad), pero el equipo finalmente lo demostró. No solo mostraron que para cada fuerza repulsiva hay exactamente una función mágica, sino que también dieron una receta para su fabricación. Como en el caso de las esferas de embalaje, este diseño dio inmediatamente certificados de optimización para el E ₈ y la red Lich. "Es una especie de resultado monumental", dijo Schwartz.

Rejilla triangular

Además de resolver el problema de la optimización universal, una nueva prueba responde a la pregunta urgente que los matemáticos han enfrentado desde que Vyazovskaya resolvió el problema de empacar esferas hace tres años: ¿de dónde viene su función mágica? "Creo que muchos estaban perplejos", dijo Vyazovskaya. "Preguntaron: ¿Cuál es el punto de esto?"

En un nuevo trabajo, Vyazovskaya y sus colegas demostraron que la función mágica de empacar esferas es la primera de una serie de bloques de construcción de formas modulares que se pueden usar para crear funciones mágicas para cada fuerza repulsiva. "Ahora tiene muchos hermanos y hermanas", dijo Vyazovskaya.

A Kon todavía le parece maravilloso que la imagen haya funcionado tan bien. "En matemáticas, algunas cosas deben lograrse mediante la perseverancia y la fuerza bruta", dijo. "Y hay momentos, como ahora, como si las matemáticas quisieran que algo sucediera".

La siguiente pregunta natural es si estos métodos se pueden adaptar para probar la optimización universal para el único candidato restante: redes de triángulos equiláteros en un plano bidimensional. Para los matemáticos, el hecho de que nadie haya podido presentar pruebas en condiciones tan simples se considera "una vergüenza terrible para toda la comunidad", dijo Edward Saff , matemático de la Universidad de Vanderbilt en Nashville.

A diferencia de E ₈ y la red Leach, una red triangular bidimensional aparece en diferentes lugares de la naturaleza, desde las estructuras celulares hasta la ubicación de los embudos en los superconductores. Los físicos ya implican la optimización de esta red en una amplia gama de contextos basados ​​en una montaña de experimentos y simulaciones. Pero, dice Cohn, nadie tiene una explicación conceptual de por qué una red triangular debería ser universalmente óptima, algo que, con suerte, proporcionará una prueba matemática.

La dimensión 2 es la única, con la excepción de 8 y 24, en la que el límite inferior numérico de Kohn y Kumar funciona bien. Esto sugiere claramente que una función mágica debe existir en dos dimensiones. Sin embargo, el método de comando para construir funciones mágicas difícilmente se puede transferir a esta nueva área: depende en gran medida del hecho de que los números que denotan las distancias entre los puntos en E ₈ y el enrejado de Lich se comportan especialmente bien, lo que no sucede en dos dimensiones. Hasta ahora, esta dimensión "parece estar más allá de las capacidades humanas", dijo Cohn.

Hasta ahora, los matemáticos están celebrando su nueva visión asociada con los extraños mundos de los espacios de 8 y 24 dimensiones. Esto, como dijo Schwartz, es "una de las mejores cosas que probablemente veré en mi vida".