Dejar de usar RSA

Hola% username%!

RSA es el primer algoritmo de criptografía asimétrica ampliamente utilizado que todavía es popular en la industria. Es relativamente simple a primera vista. El cifrado y la firma RSA se pueden contar en una hoja de papel, que los estudiantes suelen hacer en el trabajo de laboratorio.
Pero simplemente hay una gran cantidad de matices sin los cuales incluso un niño puede descifrar su implementación RSA.

Por alguna razón, la gente todavía piensa que RSA es un buen algoritmo. Pero, de hecho, el alcance de un tiro en la pierna cuando se implementa RSA es extremadamente grande. Los parámetros débiles son difíciles de verificar, si no imposibles. Y el bajo rendimiento del algoritmo alienta a los desarrolladores a utilizar formas arriesgadas para mejorarlo.

Peor aún, los ataques de oráculo de relleno que se inventaron hace más de 20 años siguen siendo relevantes hoy en día.
Incluso si en teoría es posible implementar RSA correctamente, en la práctica, tal "hazaña" es casi imposible de lograr. Y las vulnerabilidades que han estado surgiendo constantemente durante décadas solo han confirmado esto.

Algunas palabras sobre el algoritmo RSA

Si sabe cómo funciona RSA, puede omitir esta parte.

RSA es un criptosistema de clave pública que tiene dos usos.

El primero es el cifrado, cuando Alice publica su clave pública y Bob, al saberlo, puede cifrar un mensaje que solo Alice puede leer, descifrándolo con su clave privada.

La segunda es una firma digital, que le permite a Alice firmar el mensaje con su clave privada para que todos puedan verificar esta firma con su clave pública.

Ambos algoritmos difieren en detalles insignificantes, por lo tanto, los llamaremos simplemente RSA.

Para comenzar a trabajar con RSA, Alice debe elegir dos primos p y q , que juntos forman un grupo de números módulo N = pq . Entonces Alice necesita elegir un exponente abierto ey un exponente secreto d tal que $$$ed = 1 \ mod (p-1) (q-1)$. En esencia, eyd deberían ser mutuamente simples.

Una vez que se seleccionan estas opciones, Bob puede enviar a Alice un mensaje M, computando $$$C = M ^ e (mod \ N)$. Alice puede descifrar el mensaje computando $$$M = C ^ d (mod \ N)$.
La firma digital es exactamente lo contrario. Si Alice quiere firmar el mensaje, ella calcula la firma $$$S = M ^ d (mod \ N)$Bob puede verificar asegurándose de que el mensaje $$$M = S ^ e (mod \ N)$

Eso es todo, esa es la idea principal. Volveremos a los oráculos de relleno más tarde, pero por ahora veamos qué se puede hacer si los parámetros RSA se seleccionan incorrectamente.

Principio del fin

Para que RSA funcione, debe seleccionar bastantes parámetros. Desafortunadamente, los métodos aparentemente inocentes de su elección pueden dañar la seguridad. Veamos cada uno de ellos y veamos qué sorpresas desagradables te esperan.

Primera generación

La seguridad de RSA se basa en el hecho de que tener un gran número de N , que es el producto de dos primos p y q , descomponer N en factores primos sin conocer pyq es difícil de hacer. Los desarrolladores son responsables de elegir los números primos que componen el módulo RSA. Este proceso es extremadamente lento en comparación con la generación de claves para otros protocolos criptográficos, donde es suficiente simplemente seleccionar unos pocos bytes aleatorios. Por lo tanto, en lugar de generar un número primo verdaderamente aleatorio, los desarrolladores a menudo intentan crear números de cierta forma. Casi siempre termina mal. Hay muchas formas de elegir números primos para que factorizar N sea simple. Por ejemplo, pyq deben ser globalmente únicos. Si p o q alguna vez se reutilizan en otros módulos RSA, ambos factores pueden calcularse fácilmente utilizando el algoritmo GCD. Los generadores de números aleatorios incorrectos hacen que este escenario sea bastante probable, y los estudios han demostrado que aproximadamente el 1% del tráfico TLS en 2012 estuvo expuesto a dicho ataque.

Además, pyq deben seleccionarse independientemente uno del otro. Si pyq comparten aproximadamente la mitad de sus bits más significativos, entonces N puede calcularse utilizando el método Fermat. De hecho, incluso elegir un algoritmo de prueba de simplicidad puede tener implicaciones de seguridad. Quizás el ataque más publicitado es la vulnerabilidad ROCA en RSALib, que afectó a muchas tarjetas inteligentes, módulos de plataforma confiables e incluso claves Yubikey. Aquí, cuando se generan claves, solo se utilizan números primos de cierta forma para acelerar los cálculos. Los números primos generados de esta manera son triviales de descubrir utilizando técnicas complicadas en teoría de números. Una vez que se ha reconocido un sistema débil, las propiedades algebraicas especiales de los números primos permiten a un atacante usar el método Coppersmith para descomponer N.

Debe tenerse en cuenta que en ninguno de estos casos, la generación de números primos de esta manera es un hecho obvio que conduce a una falla completa del sistema. Esto se debe a que las propiedades teóricas numéricas insignificantes de los números primos tienen un impacto significativo en la seguridad de RSA. La expectativa de que un desarrollador común navegue por este campo minado matemático socava seriamente la seguridad.

Expositor secreto d

Dado que el uso de una clave privada grande afecta negativamente el tiempo de descifrado y firma, los desarrolladores tienen un incentivo para elegir una pequeña d , especialmente en el caso de dispositivos con bajo consumo de energía, como las tarjetas inteligentes. Sin embargo, un atacante puede recuperar la clave privada cuando d es menor que la raíz de 4º grado de N. En cambio, los desarrolladores deberían elegir un valor grande de d , de modo que el teorema del resto chino pudiera usarse para acelerar el descifrado. Sin embargo, la complejidad de este enfoque aumenta la probabilidad de errores menores de implementación que pueden conducir a la recuperación de claves.

¿Dice que generalmente durante la inicialización de RSA primero genera un módulo, usa un exponente abierto fijo y luego elige un secreto?
Sí, esto evita ataques con un pequeño exponente secreto si siempre usa uno de los exponentes abiertos recomendados e .
Desafortunadamente, esto también supone que los desarrolladores realmente harán esto. En el mundo real, los desarrolladores a menudo hacen cosas extrañas, por ejemplo, primero eligen d y luego consideran e .

Expositor abierto e

Al igual que con el expositor secreto, los desarrolladores desean utilizar pequeños expositores abiertos para ahorrar en el cifrado y la verificación de firmas. Típicamente, los primos de Fermat se usan en este contexto, en particular e = 3, 17 y 65537.

A pesar del hecho de que los criptógrafos recomiendan usar 65537, los desarrolladores a menudo eligen e = 3, lo que conduce a muchas vulnerabilidades en el criptosistema RSA.


(Aquí, los desarrolladores usaron e = 1, que en realidad no cifra el texto plano).

Cuando e = 3 o un tamaño similar, muchas cosas pueden salir mal. Los pequeños exponentes abiertos a menudo se combinan con otros errores comunes que permiten que un atacante descifre ciertos textos cifrados o factor N.

Por ejemplo, un ataque de Franklin-Reuters permite a un atacante descifrar dos mensajes que están conectados por una distancia conocida y fija. En otras palabras, supongamos que Alice envía a Bob solo "comprar" o "vender". Estos mensajes se asociarán con un valor conocido y permitirán que un atacante determine cuál de ellos significa "comprar" y qué "vender" sin descifrar el mensaje. Algunos ataques con e pequeña pueden incluso conducir a la recuperación de claves.

Si el exponente abierto es pequeño (no solo 3), un atacante que conoce varios bits de la clave secreta puede recuperar los bits restantes y romper el sistema criptográfico. Aunque muchos de estos ataques e = 3 RSA se pueden solucionar mediante relleno, los desarrolladores que implementan el RSA ellos mismos a menudo olvidan usarlo.

Las firmas RSA también son vulnerables a los pequeños expositores públicos. En 2006, Bleichenbacher descubrió un ataque que permite a los atacantes falsificar firmas arbitrarias en muchas implementaciones de RSA, incluidas las utilizadas en Firefox y Chrome. Esto significa que cualquier certificado TLS de una implementación vulnerable puede ser manipulado. Este ataque explota el hecho de que muchas bibliotecas usan un pequeño exponente público y no realizan una simple verificación de alineación cuando procesan firmas RSA. El ataque de Bleichenbacher a la firma es tan simple que se incluye en muchos ejercicios en cursos de criptografía.

Elegir opciones es una tarea difícil

Es común a todos estos ataques a los parámetros que el número total de posibles variantes de parámetros sea mucho mayor que el número de variantes seguras.

Se supone que los propios desarrolladores gestionarán este complejo proceso de selección, ya que todo, excepto el exponente abierto, debe generarse durante la inicialización.
No hay formas fáciles de verificar la confiabilidad de los parámetros . En cambio, los desarrolladores necesitan una base matemática seria, cuya presencia no debe esperarse de los empleados comunes. Si bien el uso de RSA con alineación puede salvarlo si tiene los parámetros incorrectos, muchos prefieren no hacerlo.

Relleno de ataques de Oracle

Como explicamos anteriormente, simplemente usar RSA fuera de la caja no funciona del todo. Por ejemplo, el esquema RSA descrito en la introducción creará textos cifrados idénticos si el mismo texto sin formato alguna vez se ha cifrado más de una vez. Esto es un problema porque permitirá que un atacante aprenda el contenido de un mensaje del contexto, sin poder descifrarlo. Es por eso que necesitamos alinear los mensajes con unos pocos bytes aleatorios. Desafortunadamente, el esquema de alineación más utilizado, PKCS # 1 v1.5, a menudo es vulnerable al llamado ataque del oráculo de relleno.

El ataque inicial contra PKCS # 1 v1.5 fue descubierto en 1998 por Daniel Bleikhanbacher. A pesar de que tiene más de 20 años, hoy sigue siendo relevante para muchos sistemas. Las versiones modernas de este ataque a menudo incluyen un oráculo adicional, un poco más complicado que el descrito originalmente por Bleikhanbacher, por ejemplo, el tiempo de respuesta del servidor o la ejecución de cualquier degradación de protocolo en TLS. Un ejemplo particularmente impactante fue el ataque ROBOT , que fue tan terrible que un equipo de investigadores pudo firmar mensajes con las claves secretas de Facebook y PayPal. Algunos podrían argumentar que esto no es realmente culpa de RSA: las matemáticas básicas están bien; la gente simplemente estropeó un estándar importante hace décadas. El hecho es que ya teníamos , desde 1998, un esquema de alineación estándar con evidencia de seguridad estricta, OAEP. Pero casi nadie lo usa. Incluso cuando esto sucede, es de conocimiento común que OAEP es difícil de implementar, y a menudo es vulnerable a un ataque de Manger, que es otro ataque de oráculo que se puede usar para recuperar texto sin formato.

El problema fundamental aquí es que la alineación es necesaria cuando se usa RSA, y esta complejidad adicional abre un gran margen para los ataques al sistema criptográfico. El hecho de que un poco de información, "si el mensaje se alineó correctamente", puede tener un impacto tan grande en la seguridad que hace que el desarrollo de bibliotecas seguras sea prácticamente imposible. TLS 1.3 ya no es compatible con RSA, por lo que podemos esperar menos ataques de este tipo en el futuro.

Pero mientras los desarrolladores continúen usando RSA en sus propias aplicaciones, los ataques de Padding Oracle continuarán ocurriendo.

Que hacer

Las personas a menudo prefieren usar RSA porque lo encuentran conceptualmente más simple que el protocolo DSA enrevesado o la criptografía de curva elíptica (ECC). Pero aunque RSA es más intuitivo, realmente carece de protección contra los tontos.

En primer lugar, una idea errónea común es que la elíptica es muy peligrosa, porque elegir una curva incorrecta puede anular todo. Es cierto que la selección de curvas tiene un gran impacto en la seguridad, pero uno de los beneficios de usar ECC es que la selección de parámetros se puede hacer públicamente. Los criptógrafos eligen los parámetros por usted, por lo que los desarrolladores solo necesitan generar bytes aleatorios de datos para usarlos como claves. Los desarrolladores pueden construir teóricamente una implementación de ECC con parámetros terribles y no podrán verificar cosas como puntos de curva incorrectos, pero generalmente no lo hacen. La explicación probable es que la matemática detrás de ECC es tan compleja que muy pocas personas se sienten lo suficientemente seguras para implementarla. En otras palabras, este miedo obliga a las personas a usar bibliotecas creadas por criptógrafos que conocen sus cosas. RSA, por otro lado, es tan simple que puede implementarse (mal) en una hora.

En segundo lugar, cualquier combinación de claves o esquema de firma basado en Diffie-Hellman (incluidas las opciones de curva elíptica) no requiere alineación y, por lo tanto, es totalmente resistente a los ataques de Padding Oracle. Esta es una gran victoria, dado que el RSA tiene un historial muy largo de intentos de evitar esta clase de vulnerabilidades.

Recomendamos utilizar Curve25519 para el intercambio de claves y ed25519 para las firmas digitales. El cifrado se debe realizar utilizando el protocolo ECIES, que combina el intercambio de claves ECC con un algoritmo de cifrado simétrico. Curve25519 fue diseñado para prevenir completamente las clases de ataque que podrían ocurrir a otras curvas, y también es muy rápido. Además, se implementa en muchas bibliotecas, por ejemplo, libsodium, que está equipada con documentación fácil de leer y está disponible en la mayoría de los idiomas.

Deje de usar RSA. En serio

(Twilio todavía usa claves RSA)


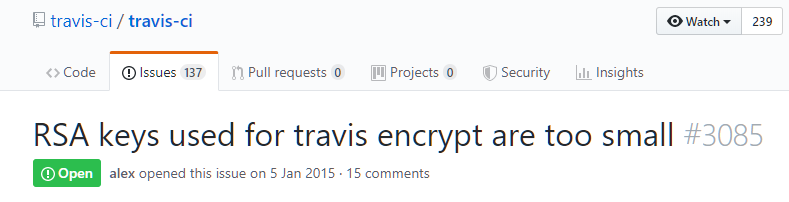
(Travis CI todavía usa claves de 1024 bits y no permite reemplazarlas)

RSA fue un hito importante en el desarrollo de comunicaciones seguras, pero las últimas dos décadas de investigación criptográfica lo han vuelto obsoleto. Los algoritmos en las curvas elípticas para el intercambio de claves y las firmas digitales se estandarizaron en 2005 y desde entonces se han integrado en bibliotecas que son intuitivas y resistentes al mal uso, como libsodium. El hecho de que RSA todavía se use ampliamente hoy en día indica tanto un error por parte de los criptógrafos debido a una descripción inadecuada de los riesgos inherentes a RSA como a los desarrolladores que sobreestiman su capacidad para implementarlo con éxito. La comunidad de seguridad debería comenzar a considerarlo como un problema de rebaño, aunque algunos de nosotros podamos navegar el proceso extremadamente peligroso de configurar o implementar RSA, las excepciones dejan en claro a los desarrolladores que RSA sigue siendo relevante de alguna manera. A pesar de las muchas advertencias y advertencias sobre StackExchange y GitHub README, muy pocas personas creen que son ellos quienes estropearán el RSA y, por lo tanto, continúan actuando imprudentemente. En última instancia, sus usuarios pagarán por ello. Es por eso que todos debemos estar de acuerdo en que usar RSA en 2019 es completamente inaceptable. Sin excepciones

Artículo original en inglés.

VirgilSecurity, Inc. Desarrolla un SDK amigable para desarrolladores de código abierto y servicios de protección de datos. Permitimos que los desarrolladores utilicen algoritmos existentes con un riesgo de seguridad mínimo.

PD: te recomiendo que también leas acerca de incrustar una puerta trasera en la clave pública RSA.