Geekly articles weekly

Un modelo de una serie natural de números y sus elementos. Rombos


   

En este trabajo, se retiene el modelo básico G 2 ± , pero se acepta una organización diferente de sus celdas (otra figura). En la parte superior de la red primaria con celdas 1 × 1 , se representa una cuadrícula más grande: se considera una cuadrícula de rombos y también una cuadrícula de centros de rombos (SCR). La última cuadrícula no se representa para no sobrecargar las líneas con el patrón con rombos. No repetiremos las definiciones y conceptos que se describieron en detalle en trabajos anteriores , pero daremos enlaces que apuntan a estos trabajos.

Descripción constructiva del modelo

A través de las celdas G 2 ± - modelos contenidos en diagonales incluso largas D i y cortas K i con números que terminan en ceros dentro del submodelo G 2 - , se dibujan líneas que forman una gran red de rombos en el plano. Las regiones rómbicas para las células cubren colectivamente todo el plano sin espacios. Cada rombo contiene 41 células, de las cuales solo 16 son de interés, y al sondear un rombo, solo se usan 4 células con flexión fija.

Las características de los rombos incluirán:

  • el número de células en el rombo;
  • el valor del número en la celda central;
  • los números de su horizontal ( N i ) y vertical ( V i );
  • identificar celdas para números con inflexiones 1, 3, 7, 9;
  • Las coordenadas de estas células en el sistema de coordenadas del rombo con el origen en la célula central del rombo.

Una cuadrícula de centros de rombos también se construye a través de las celdas de los centros de rombos, cuyos nodos se encuentran en las celdas en la intersección de diagonales largas y cortas con números que son múltiplos del número 5.
De la figura con rombos queda claro qué tipo de cuadrícula está involucrada. Para ilustrar las características de los rombos, se proporcionan imágenes de un par de rombos en cada semiplano. Estos rombos están marcados con números identificativos de células en la mitad inferior y otro par de rombos en los medios planos superiores. La marca de rombos en el semiplano debajo de la diagonal D 0 difiere de la marca de rombos en el semiplano por encima, pero dentro del mismo semiplano, la marca de todos los rombos es idéntica para los semiplanos inferior y superior. La esencia del marcado es la localización de celdas con números que tienen inflexiones iguales (marcadas al llenar las celdas con el mismo color), estableciendo sus coordenadas x 1 , x 0 . Los rombos designados se denominarán fundamentales; a partir de ellos se pueden formar otros rombos con zoom.

Los centros de los rombos del semiplano inferior son celdas con números que terminan en dos dígitos, ya sea 25 con el número horizontal con flexión 5 y con el número vertical con flexión 0, o 75 con el número horizontal con flexión 0 y con el número vertical con flexión 5. En el semiplano superior 2 + - submodelos, todos los números en las celdas centrales de todos los rombos terminan con dos dígitos 25. Además, restringimos nuestra consideración al semiplano 2 - .


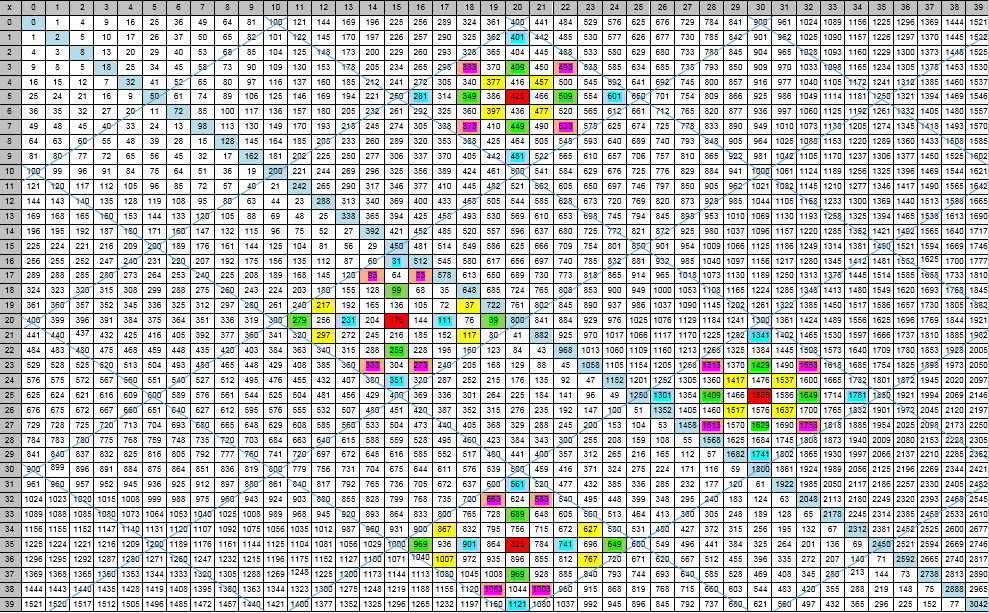Figura 1: representación visual de un modelo de diamante

Definición 1. El rombo fundamental es la estructura del modelo 2 ± -, limitada por dos diagonales cortas y dos largas de este plano con números que son múltiplos del número 10. El elemento principal que caracteriza al rombo es la celda ( x 1c , x 0c ) de su centro. El centro contiene un valor numérico de N, un múltiplo de 5.

Definición 2. El conjunto de centros de rombos fundamentales son los nodos (celdas) de la red de centros de rombos (SCR) de diagonales cortas y largas que se cruzan, con números que son múltiplos de 5. Los rombos cubren completamente el plano 2 ± - modelos (principio de parquet).

Todos los rombos están dispuestos de la misma manera, y los números en sus celdas con terminaciones fijas se colocan en posiciones fijas (celdas). Esto le permite factorizar fácilmente este número al resolver el problema de localizar el número N en un rombo determinado. Diez horizontales cuyas células forman un rombo y rombos vecinos (con coordenadas diferentes de él) se denominarán una franja de rombos. Se consideran bandas horizontales: oeste-este (); vertical: Norte-Sur (NO), a lo largo de diagonales cortas: Noreste (NE) y a lo largo de diagonales largas: Noroeste (NO). El desplazamiento de un rombo a otro se puede complementar con una indicación (arriba y abajo) a lo largo de las bandas indicadas, además de indicar la tira.

Como se deduce de la definición 2 que el conjunto de celdas de todos los rombos son todas las celdas del modelo G 2 ± , entonces, en una de las celdas (x 1p , x 0p ) que pertenecen a cierto rombo, un número natural impar compuesto (ELF) N predeterminado ( x 1p , x 0p ) = N (x 1 , x 0 ) . Al mismo tiempo, creemos que es posible indicar tal rombo (determinando las coordenadas de su celda central) (x 1c , x 0c ) que sondear todas las celdas, incluso confinándose a sondear solo diagonales impares.

La indicación de tal rombo y la celda deseada dentro de él es una solución al problema de localización para un número dado N (x 1 , x 0 ) . Este problema y su solución preceden a la recepción de la decisión de la WFCH. El significado y el objetivo final del problema de localización es indicar en un rombo determinado para un ELF N (x 1 , x 0 ) determinado los valores de las coordenadas de la celda (x 1p , x 0p ) en el modelo G 2 ± , en el que hay un número que coincide con N (x 1 , x 0 ) .

En este artículo, utilizamos el mecanismo para establecer la pertenencia de un número N dado a un rombo específico y una célula en él. Este mecanismo está lejos de ser el mejor, pero en los ejemplos propuestos hace frente a la tarea. Los lectores están invitados a ofrecer su original o mejorar este mecanismo.

Nuestro mecanismo se basa en la notable regularidad del modelo G 2 ± descubierto por el autor: la presencia en las líneas horizontales con números que son múltiplos de cinco (y algunos otros), celdas con cuadrados de los elementos de los triples pitagóricos (PFT) < g, k 1 , k 2 > = <hipotenusa , pierna 1 , pierna 2 >. El CFT se discutirá en otro trabajo.

Para simplificar las conclusiones y los cálculos, necesitaremos tres sistemas de coordenadas: plano, que ya se ha introducido , red con otros números de diagonales para el SCR (Fig.2) y rómbico (Tabla 1), en el que el comienzo está asociado con la celda del centro del rombo.


Figura 2. Numeración (doble) de diagonales cortas y
distribución de centros de diamantes en diagonales cortas

Tabla 1. Determinación de las coordenadas de un punto de búsqueda dentro de un rombo fijo



En el sistema SCR, se indica lo siguiente: el número de la diagonal corta n p , c es el número de serie del centro en él, así como el número central C de toda la red, su propia numeración de diagonales cortas a partir de n p = 1 (en el sistema plano es la quinta diagonal corta) , entonces el número n p = 2 (este es el número aumentado en 10, es decir, el decimoquinto plano K i ) y luego con el paso 10 todos los demás. La posición de todas las celdas de los centros de rombos en cada Ki del SCR también está numerada de c = 1 a c = 2n p del número de red doble de la diagonal corta.

Ejemplo 1 Sea necesario encontrar el número C de toda la red del centro de uno de los rombos y el número N en esta celda para una diagonal corta dada que pasa por los centros de rombos, su número de red n p = 5 y el número de serie del centro c = 3 de uno de los rombos en él. En pocas palabras, las coordenadas de red de la celda central de este rombo se representan en la forma (n p , q) = (5, 3) .

  1. Encuentre la coordenada del plano x 1 de la celda al comienzo de la diagonal dada (nd):
    x 1 = x nd = 10n p - 5 = 50 - 5 = 45.
    Para nuestro caso, tenemos x 1 = x nd = 45 .
  2. Ahora podemos proceder inmediatamente a la búsqueda de las coordenadas planas de la celda ( x 1c , x sc ) del centro deseado: x 1 = x nd - 5 (c - 1) = 45 - 5 (3 - 1) = 35, x 0 = 0 + 5 ( μ - 1) = 2 ∙ 5 = 10.
  3. Encuentra el número de red del centro del rombo ( C ).

    Observación Se sabe que para el número x la fórmula 2C x + 1 2 = x (x + 1) es el número duplicado de combinaciones de x + 1 en dos.
    El número de centros que preceden a la diagonal corta n p = 5 es 2n p (n p - 1) . Entonces el número de serie C del centro de red viene dado por la fórmula
    C = n p (n p -1) + c = 2C n p 2 + 3 = 5 ∙ 4 + 3 = 23 .
  4. Encuentre el valor del número N (x 1c , x sc ) en la celda del centro del rombo N = x 1 2 - x 0 2 - el signo en la fórmula se toma dependiendo de la posición del centro con respecto a la diagonal principal.
    N = 35 2 - 10 2 = 1125 - para nuestro caso.

Por lo tanto, teniendo solo el número de red n p de la diagonal corta que pasa a través de las celdas de los centros y el número de centro actual del rombo c en esta diagonal, podemos obtener toda otra información sobre el centro del rombo.

Todos los enteros positivos impares de interés N pertenecen a las células de diamante. El concepto de flexión, el último dígito de un número, permite localizar su posición dentro de los rombos. Para la factorización, esos números N que terminan con los números 1, 3, 7, 9 son de interés.

Los números pares no se consideran N , ya que tienen un divisor primo 2. Los números que terminan en cinco tienen un divisor primo 5, que también es inaceptable para N. Es aconsejable localizar un N específico por inflexión dentro del rombo en relación con el centro del rombo, en el contexto del hecho de que el centro es la característica más importante del rombo. Basado en el hecho de que todos los rombos tienen la misma estructura, existe una relación explícita entre el número N especificado para la factorización y los números en celdas de rombos con ciertas inflexiones y en la celda del centro de rombos. Los datos sobre tales números de relación se dan en la tabla. 1)

Sin embargo, clasificar todos los rombos en un avión para encontrar el rombo deseado es inaceptable, ya sea a tiempo o en costo computacional. Así, surgió el problema de localizar las regiones 2 - - submodelos (semiplanos), incluidos los rombos que contendrían el número inicial N , para ser factorizados.

Los pitagóricos se triplican . Para resolver el problema formulado se utilizan
Los triples pitagóricos son triples de números que satisfacen el teorema de Pitágoras: a saber, triples pitagóricos que satisfacen la regla del llamado triángulo egipcio, es decir, un triángulo con lados que son múltiplos de 3, 4, 5.
En cada x 1 horizontal que contiene los centros de rombos, hay uno o más de estos triples pitagóricos.

El primer rombo en el problema de localización se indica aproximadamente y, en caso de una "falla", se deben seleccionar los siguientes rombos. Para esto, es necesario determinar la dirección del movimiento a lo largo del SCR, para acercarse gradualmente a la meta final. Por ejemplo, si el menor de los 4 en el rombo actual de números es menor que el N dado, entonces los rombos del noreste y del este contienen incluso menos de 4 números, es decir, tales rombos no deben ser sondeados. Mudarse al rombo occidental conduce a un aumento tan grande de los valores en las 4 celdas que incluso un número menor del rombo occidental resulta ser mayor que el número mayor del rombo anterior y, por lo tanto, más que N. De ahí la solución: subir del rombo al rombo en la dirección noroeste.

Si se encuentra un rombo que contiene una celda con un número igual a N (x 1p , x 0p ) = N y se determinan las coordenadas de la celda (x 1p , x 0p ) , entonces la solución del FBCH está determinada por la relación básica 2 ± - del modelo
N = x 2 1 - x 2 0 = (x 1 - x 0 ) (x 1 + x 0 ) = p ∙ q

Otro subproblema es la selección e implementación de la secuencia de derivación celular del rombo seleccionado para el sondeo. Aquí, se adopta el orden transversal en sentido antihorario, comenzando desde la celda superior izquierda que contiene el número con la inflexión requerida. En una situación de coincidencia de los valores en la celda de diamante N (x 1p , x 0p ) y un número dado N (x 1 , x 0 ), la diferencia entre ellos resulta ser cero.

Algoritmo de solución ZFBCH utilizando rombos fundamentales y PFT

  1. Extraemos la raíz del número N. Redondear hacia abajo.
  2. Verificamos si √N es divisible por 3. Si es divisible, entonces asigne este valor al primer tramo k1, de lo contrario, para cumplir con la propiedad de divisibilidad por 3, reste 1 o 2 del resultado e ingréselo en la memoria como k1. El resultado de dividir el valor completamente seleccionado por tres M = √N / 3 - recuerde el coeficiente de escala PFT.
  3. Obtenemos el valor para el segundo tramo k 2 , de acuerdo con la regla del triángulo egipcio, k 2 = 4 ∙ M.
  4. Encontramos el valor de la hipotenusa g = 5 ∙ M , y el valor x 1 = g debe dividirse por el número cinco. Como puede ver, el valor de la hipotenusa siempre es igual al número horizontal con PFT.
  5. Encuentra la coordenada x 1 = g .
  6. Después de eso, determinamos la inflexión (último dígito) del número N , φ = N (mod10) .
  7. Encontramos el centro del rombo más cercano a k1 y luego examinamos los rombos adyacentes en una de las bandas de rombos (hay 4 direcciones) para encontrar una solución.
  8. Dependiendo del tipo de inflexión que obtengamos en el párrafo 6, usamos la columna (máscara) deseada de las presentadas en la tabla. 1 para determinar las coordenadas del punto de búsqueda ( x 1p , x 0p ) y encontrar el valor del número en esta celda N p . En cada rombo, solo se verifican 4 celdas de la 41a celda.
  9. Después de establecer que el número N pertenece a un rombo en particular y a una celda en él, según la misma tabla. 1 obtenemos las coordenadas del plano N: (x 1p , x 0p ) .
  10. Usando las propiedades del modelo matemático seleccionado
    N = x 2 1 - x 2 0 = (x 1 - x 0 ) (x 1 + x 0 ) = p ∙ q
    obtenemos la representación multiplicativa de N del aditivo.
  11. Por lo tanto, a la salida del algoritmo, tenemos: N = p ∙ q . Dependiendo del valor de flexión f según las fórmulas de la tabla. 1, se determinan las coordenadas del punto (x 1p , x 0p ) y se calcula la diferencia ∆ = N (x 1p , x 0p ) - N (x 1 , x 0 ) . Si ∆ ≠ 0 , entonces vaya a otra celda, si todas las celdas del rombo están marcadas, entonces a otro rombo.
    Si Δ = 0 , entonces x 1 = x 1p , x 0 = x 0p yp = (x 1 - x 0 ) , q = N / p = (x 1 + x 0 ) .

Ejemplo 2. Dado: N = 1037 , un número con una capacidad de 4. Se requiere factorizarlo. Actuamos de acuerdo con el algoritmo dado.

  1. Extraemos la raíz de N : √N = 32.202 . Redondeamos hacia abajo: √N = 32 .
  2. Verificamos si 32 es divisible por 3. Como 32 no es divisible por 3, restamos 2. Entonces, suponemos que la primera pata es k 1 = 3 ∙ 10 = 30 , aquí M = 10 = 30/3 es el factor de escala PFT .
  3. Obtenemos el valor para el segundo tramo k 2 = 4 ∙ 10 = 40 .
  4. Encontramos el valor de hipotenusa g = (k 2 1 + k 2 2 ) 0.5 , siempre que esté dividido entre 5, (30 2 +40 2 ) 0.5 = 50.
  5. Por lo tanto, x1 = k1 = 50 y la PFT se transforma en la forma g = 50 , k 1 = 30, k 2 = 40 .
  6. Encontramos la inflexión del número N : φ (1037) = 1037 (mod10) = 7 .
  7. Encontramos el centro del rombo más cercano a N = 1037 .
    Tendrá las coordenadas de la celda central del rombo: x 1 = 50, x 0 = 35 . La primera coordenada es el número de línea que contiene el CFT. El cuadrado de la pata más pequeña es 900, está contenido en la vertical con el número 40. La celda con el número 957 que termina con el siete más cercano a 900 se encuentra en la horizontal anterior con el número 49 y en la vertical con el número 38. Este es el número más pequeño de 4 en el rombo y con inflexión 7. Aquí usamos los datos de la tabla 1. El centro más cercano del rombo debe ser tres celdas a la izquierda, es decir, pertenece a la vertical 38 - 3 = 35, esta es la segunda coordenada del centro del rombo. El valor del número en la celda del centro del rombo es N (50, 35) = 1275

    Este es un rombo que tiene cuadrados de patas k1 yk2 en sus bordes. Dentro de este rombo, min es un número que termina en siete 957 en una celda ( x 1 = 49, x 0 = 38 ), y otro número en esta vertical que termina en 7th 1157 , los números grandes 1377 y 1577 se encuentran a la izquierda de la celda central, coincidiendo con el número N = 1037 no, por lo tanto, es necesario elevarse al rombo a la izquierda y más arriba con el valor en la celda central 1125 y con las coordenadas de la celda central ( x 1 = 50 - 5 = 45, x 0 = 35 - 5 = 30 ) Verifique los cuatro números para flexión 7 Estos son 847, 1027, 1207 y 1387 y no hay coincidencias con N = 1037 en este rombo), nos elevaremos aún más en la misma dirección a lo largo de la franja de rombo NW. La celda central del nuevo rombo tiene un valor de 975 y coordenadas ( x 1 = 45-5 = 40, x 0 = 35-5 = 25 ). Verificamos en este rombo los cuatro números para la inflexión 7. Esto es 737, 897, 1197 y finalmente obtenemos 1037 en la celda ( x 1p = 39, x 0p = 22 ), obtuvimos una coincidencia completa con el N. dado

    En detalle, estas acciones están representadas por los siguientes cálculos: De acuerdo con la Tabla 1, calculamos las coordenadas de las celdas y los valores numéricos en ellas. Después de eso, encontramos las diferencias entre los valores calculados y dados de N. En el primer rombo, se calculan las 4 celdas.

    ∆ = N (x 1c -1, x 0c -3) - N (x 1 , x 0 ) = N (49.32) - 1037 = 1377 - 1037 = 340 ≠ 0,
    ∆ = N (x 1c +1, x 0c -3) - N (x 1 , x 0 ) = N (51.32) - 1037 = 1577 - 1037 = 540 ≠ 0,
    ∆ = N (x 1c +1, x 0c +3) - N (x 1 , x 0 ) = N (51.38) - 1037 = 1157 - 1037 = 120 ≠ 0,
    ∆ = N (x 1c -1, x 0c +3) - N (x 1 , x 0 ) = N (49.38) - 1037 = 957 - 1037 = - 80 ≠ 0.
    En este rombo no hay coincidencia del número N con los números en las celdas.

    Vamos al siguiente rombo con el centro en la celda (x 1c -5, x 0c -5) = (45, 30) y el valor en él N (x 1c -5, x 0c -5) = N (45, 30) = 1125 .
    ∆ = N (x 1ts -1, x 0ts -3) - N (x 1 , x 0 ) = N (44.27) - 1037 = 1207 - 1037 = 170 ≠ 0,
    ∆ = N (x 1c +1, x 0c -3) - N (x 1 , x 0 ) = N (46.27) - 1037 = 1387 - 1037 = 350 ≠ 0,
    ∆ = N (x 1c +1, x 0c +3) - N (x 1 , x 0 ) = N (46.33) - 1037 = 1027 - 1037 = - 10 ≠ 0,
    ∆ = N (x 1c -1, x 0c +3) - N (x 1 , x 0 ) = N (44.33) - 1037 = 847 - 1037 = - 190 ≠ 0.
    En este rombo, tampoco hay coincidencia del número N con los números en las celdas.

    Vamos al siguiente rombo con el centro en la celda (x 1c -5, x 0c -5) = (40, 25) y el valor en él N (x 1c -5, x 0c -5) = N (40, 25) = 975
    ∆ = N (x 1c -1, x 0c -3) - N (x 1 , x 0 ) = N (39.22) - 1037 = 1037 - 1037 = 0.
    Obtuve una diferencia de valores cero. Hay una completa coincidencia. De esto se deduce que el número dado N (x 1 , x 0 ) = 1037 está contenido en la celda con coordenadas (x 1 , x 0 ) = (39, 22). Finalmente, la solución del HFBC está determinada por la relación principal
    N = x 2 1 - x 2 0 = (x 1 - x 0 ) (x 1 + x 0 ) = (39 - 22) (39 + 22) = p ∙ q = 17 ∙ 61 .
  8. Puede actuar de manera diferente, comenzando con el rombo indicado en el párrafo 6, usando la tabla. 1, descubrimos si el número N pertenece a un rombo en particular, moviéndose entre los centros de los rombos primero horizontalmente, hacia la diagonal principal, luego bajando a la siguiente franja de rombos y repitiendo todo nuevamente.
  9. Después de establecer que el número N pertenece a cierto rombo (en nuestro caso, el rombo tendrá coordenadas ( x 1 = 40, x 0 = 25 )) basadas en la misma tabla. 1 obtenemos las coordenadas N : x 1p = 39 , x 2p = 22 (9 rombos vistos).
  10. Usando las propiedades del modelo matemático seleccionado del número
    N = x 2 1 - x 2 0 = (x 1 - x 0 ) (x 1 + x 0 ) = p ∙ q
    obtenemos la representación multiplicativa de N del aditivo:
    N = (39 - 22) (39 + 22) = 17 ∙ 61 = 1037 .

Por lo tanto, en la salida tenemos N = p · q = 17 · 61 = 1037 , es decir, la solución al problema se obtuvo con éxito.

También obtenemos el resultado de una solución de software para el problema en el Ejemplo 3.

Ejemplo 3 . Dado: N = 3808572773, un número con una resolución de 10.

  1. Extraemos la raíz de N: √N = 61713 , 64 = 61713 .
  2. Verificamos si 61713 es divisible por 3. Dado que 61713 es divisible por 3,
    6 + 1 + 7 + 1 + 3 = 18 es divisible por 3, el primer tramo k 1 es igual a k 1 = 61713 .
  3. k 2 = 4k 1 /3 => 4k 2 /3 = 82284 .
  4. g =√k 12 +k 22 , ,
    5 · g = √617132 + 822842 = 102855 .
  5. x 1 = k 1 = 61713 , k 1 = 61713, k 2 = 82284, g = 102855 .
  6. N: (3808572773) = 3808572773(mod10) = 3 .
  7. . x 1 = 61715; x 9 = 0 .
  8. , 7, . 1, N , , , , .
  9. N ( x 1 = 62015 , x 0 = 6085 ) N :
    x 1p = 62013; x 0p = 6086 ; ( 60 ).

  10. N = x 2 1 — x 2 0 = (x 1 — x 0 )(x 1 + x 0 ) =p ·q N :
    N = (62013 — 6086) · (62013 + 62086) = 55927 · 68099 = 3808572773 ;
  11. , N = p · q = 55927 · 68099 = 3808572773 , . . .

Source: https://habr.com/ru/post/459520/

More articles:


All Articles