Imagine que necesita generar un número aleatorio distribuido uniformemente del 1 al 10. Es decir, un número entero del 1 al 10 inclusive, con una probabilidad igual (10%) de cada ocurrencia. Pero, digamos, sin acceso a monedas, computadoras, material radiactivo u otras fuentes similares de números (pseudo) aleatorios. Solo tienes una habitación con gente.

Supongamos que hay un poco más de 8500 estudiantes en esta sala.

Lo más simple es preguntarle a alguien: "¡Oye, elige un número aleatorio del uno al diez!". El hombre responde: "¡Siete!". Genial Ahora tienes un número. Sin embargo, comienzas a preguntarte si está distribuido de manera uniforme.

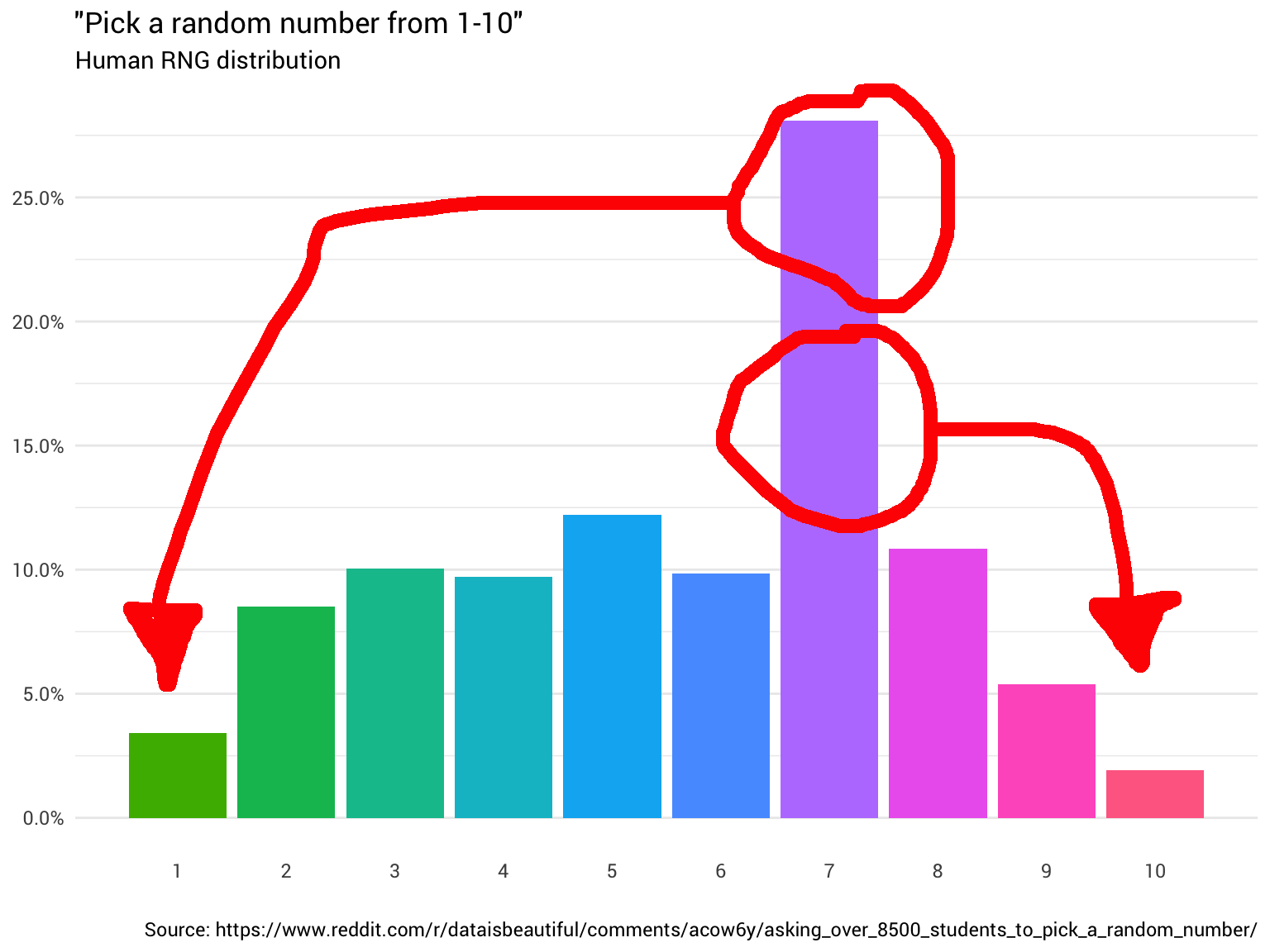
Entonces decidiste preguntarle a algunas personas más. Sigues preguntándoles y contando sus respuestas, redondeando los números fraccionarios e ignorando a aquellos que piensan que el rango del 1 al 10 incluye 0. Al final, comienzas a ver que la distribución no es ni siquiera:

library(tidyverse) probabilities <- read_csv("https://git.io/fjoZ2") %>% count(outcome = round(pick_a_random_number_from_1_10)) %>% filter(!is.na(outcome), outcome != 0) %>% mutate(p = n / sum(n)) probabilities %>% ggplot(aes(x = outcome, y = p)) + geom_col(aes(fill = as.factor(outcome))) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = '"Pick a random number from 1-10"', subtitle = "Human RNG distribution", x = "", y = NULL, caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/") 

Datos de Reddit

Te golpeas la frente. Bueno, por supuesto , no será al azar. Después de todo, no puedes confiar en las personas .

Entonces que hacer?

Desearía poder encontrar alguna función que transforme la distribución del "RNG humano" en una distribución uniforme ...

La intuición aquí es relativamente simple. Solo necesita tomar la masa de distribución de donde está por encima del 10% y moverla a donde está por debajo del 10%. Para que todas las columnas en el gráfico estén al mismo nivel:



En teoría, tal función debería existir. De hecho, debe haber muchas funciones diferentes (para la permutación). En un caso extremo, puede "cortar" cada columna en bloques infinitamente pequeños y construir una distribución de cualquier forma (como ladrillos Lego).

Por supuesto, un ejemplo tan extremo es un poco engorroso. Idealmente, queremos mantener la mayor cantidad de distribución inicial posible (es decir, hacer la menor cantidad posible de fragmentos y movimientos).

¿Cómo encontrar tal función?

Bueno, nuestra explicación anterior se parece mucho a la programación lineal . De Wikipedia:

La programación lineal (LP, también llamada optimización lineal) es un método para lograr el mejor resultado ... en un modelo matemático cuyos requisitos están representados por relaciones lineales ... La forma estándar es la forma usual y más intuitiva de describir un problema de programación lineal. Consta de tres partes:

• Función lineal a maximizar
  
• Limitaciones del problema de la siguiente forma
  
• Variables no negativas

Del mismo modo, se puede formular el problema de la redistribución.

Presentación del problema.

Tenemos un conjunto de variables $$$(x_ {i, j}$ , cada uno de los cuales codifica una fracción de la probabilidad redistribuida de un entero $$$i$ (1 a 10) a un entero $$$j$ (de 1 a 10). Por lo tanto, si $$$(x_ {7,1} = 0.2$ , entonces necesitamos transferir el 20% de las respuestas de siete a uno.

 variables <- crossing(from = probabilities$outcome, to = probabilities$outcome) %>% mutate(name = glue::glue("x({from},{to})"), ix = row_number()) variables 

  ## # Un tibble: 100 x 4
 ## de a nombre de ix
 ## <dbl> <dbl> <glue> <int>
 ## 1 1 1 x (1,1) 1
 ## 2 1 2 x (1,2) 2
 ## 3 1 3 x (1,3) 3
 ## 4 1 4 x (1,4) 4
 ## 5 1 5 x (1,5) 5
 ## 6 1 6 x (1,6) 6
 ## 7 1 7 x (1,7) 7
 ## 8 1 8 x (1,8) 8
 ## 9 1 9 x (1.9) 9
 ## 10 1 10 x (1,10) 10
 ## # ... con 90 filas más 

Queremos limitar estas variables para que todas las probabilidades redistribuidas sumen 10%. En otras palabras, para cada $$$j$ del 1 al 10:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0.1$$

Podemos representar estas restricciones como una lista de matrices en R. Posteriormente, las vinculamos en una matriz.

 fill_array <- function(indices, weights, dimensions = c(1, max(variables$ix))) { init <- array(0, dim = dimensions) if (length(weights) == 1) { weights <- rep_len(1, length(indices)) } reduce2(indices, weights, function(a, i, v) { a[1, i] <- v a }, .init = init) } constrain_uniform_output <- probabilities %>% pmap(function(outcome, p, ...) { x <- variables %>% filter(to == outcome) %>% left_join(probabilities, by = c("from" = "outcome")) fill_array(x$ix, x$p) }) 

También debemos asegurarnos de que se conserva toda la masa de probabilidades de la distribución inicial. Entonces para todos $$$j$ en el rango de 1 a 10:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0.1$$

 one_hot <- partial(fill_array, weights = 1) constrain_original_conserved <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome) %>% pull(ix) %>% one_hot() }) 

Como ya se mencionó, queremos maximizar la preservación de la distribución original. Este es nuestro objetivo :

$$

$$maximizar (x_ {1, 1} + x_ {2, 2} + \ ldots \ x_ {10, 10})$$

 maximise_original_distribution_reuse <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome, to == outcome) %>% pull(ix) %>% one_hot() }) objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums() 

Luego pasamos el problema al solucionador, por ejemplo, el paquete lpSolve en R, combinando las restricciones creadas en una matriz:

 # Make results reproducible... set.seed(23756434) solved <- lpSolve::lp( direction = "max", objective.in = objective, const.mat = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)), const.dir = c(rep_len("==", length(constrain_original_conserved)), rep_len("==", length(constrain_uniform_output))), const.rhs = c(rep_len(1, length(constrain_original_conserved)), rep_len(1 / nrow(probabilities), length(constrain_uniform_output))) ) balanced_probabilities <- variables %>% mutate(p = solved$solution) %>% left_join(probabilities, by = c("from" = "outcome"), suffix = c("_redistributed", "_original")) 

Se devuelve la siguiente redistribución:

 library(gganimate) redistribute_anim <- bind_rows(balanced_probabilities %>% mutate(key = from, state = "Before"), balanced_probabilities %>% mutate(key = to, state = "After")) %>% ggplot(aes(x = key, y = p_redistributed * p_original)) + geom_col(aes(fill = as.factor(from)), position = position_stack()) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = 'Balancing the "Human RNG distribution"', subtitle = "{closest_state}", x = "", y = NULL) + transition_states( state, transition_length = 4, state_length = 3 ) + ease_aes('cubic-in-out') animate( redistribute_anim, start_pause = 8, end_pause = 8 ) 

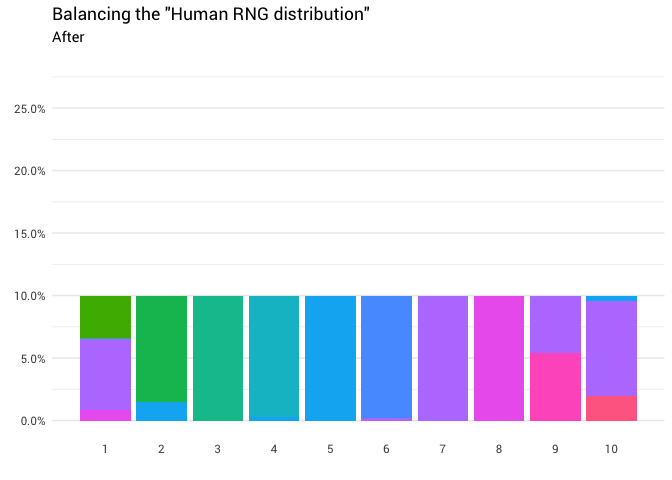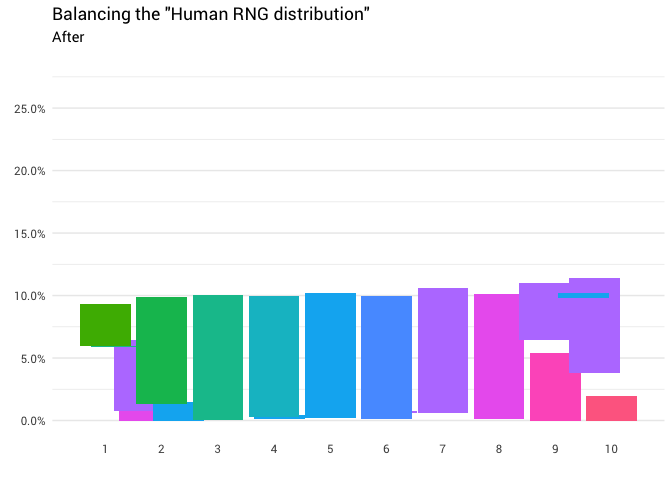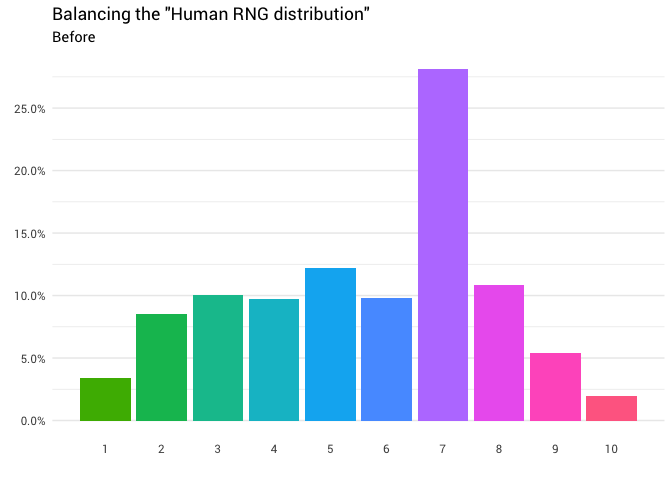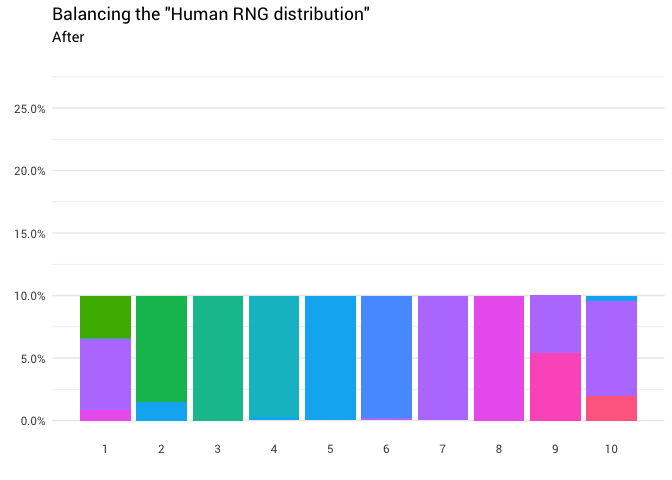
Genial Ahora tenemos una función de redistribución. Echemos un vistazo más de cerca exactamente cómo se mueve la masa:

 balanced_probabilities %>% ggplot(aes(x = from, y = to)) + geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) + geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) + scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) + scale_fill_discrete(h = c(120, 360)) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(breaks = 1:10) + theme_minimal(base_family = "Roboto") + theme(panel.grid.minor = element_blank(), panel.grid.major = element_line(linetype = "dotted"), legend.position = "none") + labs(title = "Probability mass redistribution", x = "Original number", y = "Redistributed number") 

Este cuadro dice que en aproximadamente el 8% de los casos cuando alguien llama al ocho como un número aleatorio, debe tomar la respuesta como una unidad. En el 92% restante de los casos, sigue siendo el ocho.

Sería bastante simple resolver el problema si tuviéramos acceso a un generador de números aleatorios distribuidos uniformemente (de 0 a 1). Pero solo tenemos una habitación llena de gente. Afortunadamente, si está listo para aceptar algunas inexactitudes menores, puede hacer un RNG bastante bueno de las personas sin pedir más de dos veces.

Volviendo a nuestra distribución original, tenemos las siguientes probabilidades para cada número, que se pueden usar para reasignar cualquier probabilidad, si es necesario.

 probabilities %>% transmute(number = outcome, probability = scales::percent(p)) 

  ## # Un tibble: 10 x 2
 ## probabilidad de número
 ## <dbl> <chr>
 ## 1 1 3.4%
 ## 2 2 8.5%
 ## 3 3 10.0%
 ## 4 4 9.7%
 ## 5 5 12.2%
 ## 6 6 9.8%
 ## 7 7 28.1%
 ## 8 8 10.9%
 ## 9 9 5.4%
 ## 10 10 1.9% 

Por ejemplo, cuando alguien nos da ocho como un número aleatorio, necesitamos determinar si este ocho debería convertirse en una unidad o no (probabilidad 8%). Si le preguntamos a otra persona acerca de un número aleatorio, entonces con una probabilidad del 8,5% responderá "dos". Entonces, si este segundo número es 2, sabemos que debemos devolver 1 como un número aleatorio distribuido uniformemente .

Extendiendo esta lógica a todos los números, obtenemos el siguiente algoritmo:

• Pídale a una persona un número aleatorio, $$$n_1$ .
• $$$n_1 = 1, 2, 3, 4, 6, 9,$ o $$$10$ :
  
  • Tu numero aleatorio $$$n_1$
• Si $$$n_1 = 5$ :
  
  • Pídale a otra persona un número aleatorio ( $$$n_2$ )
  • Si $$$n_2 = 5$ (12,2%):
    
    • Tu número aleatorio 2
  • Si $$$n_2 = 10$ (1,9%):
    
    • Tu número aleatorio 4
  • De lo contrario, su número aleatorio es 5
• Si $$$n_1 = 7$ :
  
  • Pídale a otra persona un número aleatorio ( $$$n_2$ )
  • Si $$$n_2 = 2$ o $$$5$ (20,7%):
    
    • Tu número aleatorio 1
  • Si $$$n_2 = 8$ o $$$9$ (16,2%):
    
    • Tu número aleatorio es 9
  • Si $$$n_2 = 7$ (28,1%):
    
    • Tu número aleatorio es 10
  • De lo contrario, su número aleatorio es 7
• Si $$$n_1 = 8$ :
  
  • Pídale a otra persona un número aleatorio ( $$$n_2$ )
  • Si $$$n_2 = 2$ (8,5%):
    
    • Tu número aleatorio 1
  • De lo contrario, su número aleatorio es 8

¡Usando este algoritmo, puede usar un grupo de personas para obtener algo cercano a un generador de números aleatorios distribuidos uniformemente del 1 al 10!